Sürekli tekdüze dağılım (İngilizce: continuous uniform distribution) olasılık kuramı ve istatistik bilim dallarında, her elemanı, olasılığın desteklendiği aynı büyüklükteki aralık içinde bulunabilir, her sürekli değer için aynı sabit olasılık gösteren bir olasılık dağılımları ailesidir. Desteklenen aralık iki parametre ile, yani minimum değer a ve maksimum değer b ile, tanımlanmaktadır. Bu dağılım kısa olarak U(a,b) olarak anılır.
Olasılık yoğunluk fonksiyonu | |
Yığmalı dağılım fonksiyonu | |
| Parametreler | |
|---|---|
| Olasılık yoğunluk fonksiyonu (OYF) | |
| Birikimli dağılım fonksiyonu (YDF) | |
| Ortalama | |
| Medyan | |
| Mod | aralığında herhangi bir değer |
| Varyans | |
| Çarpıklık | |
| Fazladan basıklık | |
| Entropi | |
| Moment üreten fonksiyon (mf) | |
| Karakteristik fonksiyon | |
Karakteristikler
Olasılık yoğunluk fonksiyonu
Sürekli tekdüze dağılım için olasılık yoğunluk fonksiyonu şöyle ifade edilir:
Sınırda olan değerler, a ve b genellikle teorik bakımdan önemli değildirler; çünkü herhangi bir aralıkta f(x) dx integral değerine ve x f(x) dx değerine ve benzer değerlerine bu sınır değerler hiçbir teorik etkide bulunmazlar. Bazen bu değerler 0 veya 1/(b - a) olarak seçilirler. İkinci alternatif yöntemi ile tahmin yapılmak gerektiği zaman pratikte kullanılır. uygulamak gerektiği zaman f(a) veya f(b) değeri 1/(2(b - a)) olarak seçilir. Böylece bu sürekli tekdüze fonksiyonun birçok ters dönüşümü sonucunda (sıfır ölçümü hariç noktaların dışında nerede ise her tarafta birbirine eşit bir fonksiyon yerine) biraz fikir karışıklığına neden olup, özel olarak seçilen tekdüze fonksiyon tekrar elde edilir. Bu çeşit tekdüze fonksiyon, daha önceki haldeki gibi anlam belirsizliği yaratmadan, işaret fonksiyonu ile de uyuşma gösterir.
Yığmalı dağılım fonksiyonu
Yığmalı dağılım fonksiyonu şöyle ifade edilir:
Üreten fonksiyonlar
Moment-üreten fonksiyon
Sürekli tekdüze dağılım için moment üreten fonksiyon şudur:
Bu fonksiyon kullanılarak şu m k sayıda ham momentleri hesaplanır:
Bir sürekli tekdüze dağılım gösteren bir rassal değişken icin bu halde beklenen değer
- m1 = (a + b)/2
olur ve varyans şudur:
- m2 - m12 = (b - a)2/12.
Kümülant üreten fonksiyon
n ≥ 2; için bir [0 1] aralığında bulunan tekdüze dağılımın ninci kümülantı bb/n, burada bnninci Bernoulli sayısıdır.
Özellikler
Borel setlere genelleştirmeler
Bu dağılım reel aralıklardan daha karmaşık setlere genelleştirilebilir. Eğer, S pozitif ve sonlu ölçümlü bir Boral seti üyesi ise S üzerindeki bir tekdüze olasılık dağılımı şöyle tanımlanır. S dışında ise, tekdüze olasılık yoğunluk fonksiyonu 0 olur, S içinde ise 1/K ye sabit olarak eşittir ve burada K S setinin olur
Sırasal istatistikler
X1, ..., XnU(0,1) dağılımından her biri örneklemler olsun. X(k) bu örneklem için kinci olsun. O zaman X(k) için olasılık dağılımı parametreleri k ve n - k + 1 olan bir Beta dağılımı olur. Bu beta dağılımının beklenen değeri
olur. yapılırken bu gerçek kullanılır.
Bu beta dağılım için varyans şöyle ifade edilir:
'Tekdüzelilik'
Bir tekdüze dağılım gösteren bir rassal değişkenin sabit uzunlukta bir aralığa düşme olasılığı, bu aralığın konumunun aralık dağılımın destek alanı tarafından kapsandığı sürece, bağımsızdır; ancak aralığın büyüklüğü bağımlıdır. Bu şöyle matematiksel olarak gösterilebilir:
Eğer X ≈ U(0,b) ise ve sabit d > 0 için, [x, x+d] [0,b]nin bir alt aralığı ise, o halde

Bu ifade xden bağımsızdır. Bu gerçek, tekdüze dağılımının isimlendirilmesinde ön planda rol oynamıştır.
Standart tekdüze dağılım
Eğer aralık parametreleri için 

İlişkili dağılımlar
Eğer X bir standart tekdüze dağılım (yani U(0,1)) gösteriyorsa:
- Y = -ln(X)/λ ifadesi λ (oran) parametresi olan bir üstel dağılım gösterir.
- Y = 1 - X1/n ifadesi 1 ve n parametreleri olan bir beta dağılımı gösterir. Bundan çıkartılan önemli bir sonuç standart tekdüze dağılımın, 1 ve 1 değerde parametreleri olan bir beta dağılımının özel bir hali olduğudur.
Diğer fonksiyonlar ile ilişkiler
Her geçiş noktası için aynı işlem kuralları kullanılığı zaman, olasılık yoğunluk fonksiyonu da şu terimleriyle de ifade edilebilir.
yahut bir ile şöyle ifade edilebilir:
İşaret fonksiyonunun geçiş noktası hakkında hiçbir fikir karışıklığı ortaya çıkmaz. Geçiş noktalarında yarı-maksimum işlem kuralı kullanılarak bir tekdüze dağılım bir işaret fonksiyonu terimleri ile şu şekilde ifade edilebilir:
Uygulamalar
Çıkarımsal istatistikte bir basit sıfır hipotezin test istatistiği olarak p-değeri kullanılırsa ve test istatistiği için dağılım sürekli ise, o zaman eğer sıfır hipotez doğru ise test istatistiği 0 ve 1 arasında sürekli standart tekdüze olarak dağılım gösterir.
Tekdüze dağılımdan örnekleme
Simülasyon denemelerinin işletilip sonuçlar alınmasında, sürekli tekdüze dağılımı kullanılması simülasyon tekniğinin vazgeçilmez bir ögesidir. Komputer hemen hepsi, üretilmesi için özel komuta(lar) içermektedir; bu aslında bir standart tekdüze (yani U(0,1)) dağılımından elde edilirler.
Eğer, u değeri bir standart tekdüze dağılımından alınan örnek bir sayı ise,
- a+(b-a)u
ifadesi a ve b parametreli bir sürekli tekdüze dağılımdan alınan rastgele bir sayı olur.
Herhangi bir dağılımdan örnekleme
Herhangi rastgele seçilmiş dağılımdan örnek alma işlemi uygulanmasında sürekli tekdüze dağılımı önemli bir rol oynar. Kullanılan bir genel yöntem ve bu yöntem hedef olan dağılım için yığmalı dağılım fonksiyonunu kullanır. Bu yöntem teorik çalışmalar için özel önem taşır. Bu yöntemi kullanırken karmaşık işlemleri gerektirebilen, hedef değişken için yığmalı dağılım fonksiyonunun tersini almak gerektedir. Daha kolay işlemleri gerektiren, özellikle yığmalı dağılım fonksiyonlarının kapalı şeklinin bilinmediği hallerde kullanılmak üzere, alternatif yöntemler geliştirilmiştir. Böyle karakterde bir yöntem dir.
Normal dağılım ters dönüşüm yönteminin etkin olarak kullanılmasına örnek olan önemli bir dağılımdır. Ancak, bu dağılım için adını taşıyan bir kesin bir dönüşüm yöntemi de bulunmaktadır. Bu yöntem kullanılarak iki bağımsız tekdüze dağılımlı rassal değişkeni ters dönüşüm yöntemi kullanılarak iki bağımsız normal dağılım gösteren rassal değişkene çevrilir.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Surekli tekduze dagilim Ingilizce continuous uniform distribution olasilik kurami ve istatistik bilim dallarinda her elemani olasiligin desteklendigi ayni buyuklukteki aralik icinde bulunabilir her surekli deger icin ayni sabit olasilik gosteren bir olasilik dagilimlari ailesidir Desteklenen aralik iki parametre ile yani minimum deger a ve maksimum deger b ile tanimlanmaktadir Bu dagilim kisa olarak U a b olarak anilir Surekli tekduze Olasilik yogunluk fonksiyonuYigmali dagilim fonksiyonuParametreler a b displaystyle a b in infty infty a x b displaystyle a leq x leq b Olasilik yogunluk fonksiyonu OYF 1b aeger a x b0eger x lt a veya x gt b displaystyle begin matrix frac 1 b a amp mbox eger a leq x leq b 0 amp mathrm eger x lt a mathrm veya x gt b end matrix Birikimli dagilim fonksiyonu YDF 0eger x lt ax ab a eger a x lt b1eger x b displaystyle begin matrix 0 amp mbox eger x lt a frac x a b a amp mbox eger a leq x lt b 1 amp mbox eger x geq b end matrix Ortalama a b2 displaystyle frac a b 2 Medyan a b2 displaystyle frac a b 2 Mod a b displaystyle a b araliginda herhangi bir degerVaryans b a 212 displaystyle frac b a 2 12 Carpiklik 0 displaystyle 0 Fazladan basiklik 65 displaystyle frac 6 5 Entropi ln b a displaystyle ln b a Moment ureten fonksiyon mf etb etat b a displaystyle frac e tb e ta t b a Karakteristik fonksiyon eitb eitait b a displaystyle frac e itb e ita it b a KarakteristiklerOlasilik yogunluk fonksiyonu Surekli tekduze dagilim icin olasilik yogunluk fonksiyonu soyle ifade edilir f x 1b a eger a x b 0eger x lt a or x gt b displaystyle f x left begin matrix frac 1 b a amp mathrm eger a leq x leq b 0 amp mathrm eger x lt a mathrm or x gt b end matrix right Sinirda olan degerler a ve b genellikle teorik bakimdan onemli degildirler cunku herhangi bir aralikta f x dx integral degerine ve x f x dx degerine ve benzer degerlerine bu sinir degerler hicbir teorik etkide bulunmazlar Bazen bu degerler 0 veya 1 b a olarak secilirler Ikinci alternatif yontemi ile tahmin yapilmak gerektigi zaman pratikte kullanilir uygulamak gerektigi zaman f a veya f b degeri 1 2 b a olarak secilir Boylece bu surekli tekduze fonksiyonun bircok ters donusumu sonucunda sifir olcumu haric noktalarin disinda nerede ise her tarafta birbirine esit bir fonksiyon yerine biraz fikir karisikligina neden olup ozel olarak secilen tekduze fonksiyon tekrar elde edilir Bu cesit tekduze fonksiyon daha onceki haldeki gibi anlam belirsizligi yaratmadan isaret fonksiyonu ile de uyusma gosterir Yigmali dagilim fonksiyonu Yigmali dagilim fonksiyonu soyle ifade edilir F x 0eger x lt ax ab a eger a x lt b1eger x b displaystyle F x left begin matrix 0 amp mbox eger x lt a frac x a b a amp mbox eger a leq x lt b 1 amp mbox eger x geq b end matrix right Ureten fonksiyonlar Moment ureten fonksiyon Surekli tekduze dagilim icin moment ureten fonksiyon sudur Mx E etx etb etat b a displaystyle M x E e tx frac e tb e ta t b a Bu fonksiyon kullanilarak su m k sayida ham momentleri hesaplanir m1 a b2 displaystyle m 1 frac a b 2 m2 a2 ab b23 displaystyle m 2 frac a 2 ab b 2 3 mk 1k 1 i 0kaibk i displaystyle m k frac 1 k 1 sum i 0 k a i b k i Bir surekli tekduze dagilim gosteren bir rassal degisken icin bu halde beklenen deger m1 a b 2 olur ve varyans sudur m2 m12 b a 2 12 Kumulant ureten fonksiyon n 2 icin bir 0 1 araliginda bulunan tekduze dagilimin ninci kumulanti bb n burada bnninci Bernoulli sayisidir OzelliklerBorel setlere genellestirmeler Bu dagilim reel araliklardan daha karmasik setlere genellestirilebilir Eger S pozitif ve sonlu olcumlu bir Boral seti uyesi ise S uzerindeki bir tekduze olasilik dagilimi soyle tanimlanir S disinda ise tekduze olasilik yogunluk fonksiyonu 0 olur S icinde ise 1 K ye sabit olarak esittir ve burada K S setinin olur Sirasal istatistikler X1 XnU 0 1 dagilimindan her biri orneklemler olsun X k bu orneklem icin kinci olsun O zaman X k icin olasilik dagilimi parametreleri k ve n k 1 olan bir Beta dagilimi olur Bu beta dagiliminin beklenen degeri E X k kn 1 displaystyle operatorname E X k k over n 1 olur yapilirken bu gercek kullanilir Bu beta dagilim icin varyans soyle ifade edilir Var X k k n k 1 n 1 2 n 2 displaystyle operatorname Var X k k n k 1 over n 1 2 n 2 Tekduzelilik Bir tekduze dagilim gosteren bir rassal degiskenin sabit uzunlukta bir araliga dusme olasiligi bu araligin konumunun aralik dagilimin destek alani tarafindan kapsandigi surece bagimsizdir ancak araligin buyuklugu bagimlidir Bu soyle matematiksel olarak gosterilebilir Eger X U 0 b ise ve sabit d gt 0 icin x x d 0 b nin bir alt araligi ise o halde P X x x d xx ddyb a db a displaystyle P left X in left x x d right right int x x d frac mathrm d y b a frac d b a Bu ifade xden bagimsizdir Bu gercek tekduze dagiliminin isimlendirilmesinde on planda rol oynamistir Standart tekduze dagilimEger aralik parametreleri icin a 0 displaystyle a 0 ve b 1 displaystyle b 1 ise ortaya cikan U 0 1 dagilimina standart tekduze dagilim adi verilmektedir Standart tekduze dagilimin bir ilgi ceken ozelligi sudur Eger u1 bir standart tekduze dagilim gosterirse o zaman 1 u1 de standart tekduze dagilim gosterir Iliskili dagilimlarEger X bir standart tekduze dagilim yani U 0 1 gosteriyorsa Y ln X l ifadesi l oran parametresi olan bir ustel dagilim gosterir Y 1 X1 n ifadesi 1 ve n parametreleri olan bir beta dagilimi gosterir Bundan cikartilan onemli bir sonuc standart tekduze dagilimin 1 ve 1 degerde parametreleri olan bir beta dagiliminin ozel bir hali oldugudur Diger fonksiyonlar ile iliskilerHer gecis noktasi icin ayni islem kurallari kullaniligi zaman olasilik yogunluk fonksiyonu da su terimleriyle de ifade edilebilir f x H x a H x b b a displaystyle f x frac operatorname H x a operatorname H x b b a yahut bir ile soyle ifade edilebilir f x 1b arect x a b2 b a displaystyle f x frac 1 b a operatorname rect left frac x left frac a b 2 right b a right Isaret fonksiyonunun gecis noktasi hakkinda hicbir fikir karisikligi ortaya cikmaz Gecis noktalarinda yari maksimum islem kurali kullanilarak bir tekduze dagilim bir isaret fonksiyonu terimleri ile su sekilde ifade edilebilir f x sgn x a sgn x b 2 b a displaystyle f x frac operatorname sgn x a operatorname sgn x b 2 b a UygulamalarCikarimsal istatistikte bir basit sifir hipotezin test istatistigi olarak p degeri kullanilirsa ve test istatistigi icin dagilim surekli ise o zaman eger sifir hipotez dogru ise test istatistigi 0 ve 1 arasinda surekli standart tekduze olarak dagilim gosterir Tekduze dagilimdan ornekleme Simulasyon denemelerinin isletilip sonuclar alinmasinda surekli tekduze dagilimi kullanilmasi simulasyon tekniginin vazgecilmez bir ogesidir Komputer hemen hepsi uretilmesi icin ozel komuta lar icermektedir bu aslinda bir standart tekduze yani U 0 1 dagilimindan elde edilirler Eger u degeri bir standart tekduze dagilimindan alinan ornek bir sayi ise a b a u ifadesi a ve b parametreli bir surekli tekduze dagilimdan alinan rastgele bir sayi olur Herhangi bir dagilimdan ornekleme Herhangi rastgele secilmis dagilimdan ornek alma islemi uygulanmasinda surekli tekduze dagilimi onemli bir rol oynar Kullanilan bir genel yontem ve bu yontem hedef olan dagilim icin yigmali dagilim fonksiyonunu kullanir Bu yontem teorik calismalar icin ozel onem tasir Bu yontemi kullanirken karmasik islemleri gerektirebilen hedef degisken icin yigmali dagilim fonksiyonunun tersini almak gerektedir Daha kolay islemleri gerektiren ozellikle yigmali dagilim fonksiyonlarinin kapali seklinin bilinmedigi hallerde kullanilmak uzere alternatif yontemler gelistirilmistir Boyle karakterde bir yontem dir Normal dagilim ters donusum yonteminin etkin olarak kullanilmasina ornek olan onemli bir dagilimdir Ancak bu dagilim icin adini tasiyan bir kesin bir donusum yontemi de bulunmaktadir Bu yontem kullanilarak iki bagimsiz tekduze dagilimli rassal degiskeni ters donusum yontemi kullanilarak iki bagimsiz normal dagilim gosteren rassal degiskene cevrilir
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State




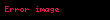
![{\displaystyle [a,b]\,\!}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4d09ESTJPR1l3TnpOa056WmxOVEF3WVRBNVlUTXdPV0UwTldKall6bG1NVGxsTlRrNVpHSTAuc3Zn.svg)