Bu madde, uygun değildir. (Aralık 2019) |
Bilineer dönüşümler, matematikte iki vektör uzayından birer eleman alıp üçüncü bir vektör uzayından bir eleman veren, ve bunu yaparken her iki girdi için de doğrusallık aksiyomlarına uyan fonksiyonlardır.
Tanım
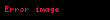







Bu tanımla şu özellikler geçerli olur:
- Her
ve her
için
'yı
'nin dışına çekmek mümkündür, yani
- Her
için
dağılma özelliğini gösterir, yani
. Aynı özellik ikinci girdi için de geçerlidir, yani her
için
geçerlidir.
Eğer 


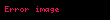





Özellikler
Doğrusallığın gereği olarak eğer 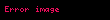



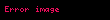







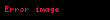


Örnekler
- Matris çarpımı,
ile
arasında bilineerdir
- Vektör iç çarpımı bilineer bir dönüşümdür. Girdileri aynı
vektör uzayından olup çıktısı
'dadır.
ile
'nin
'dan iki eleman alıp
'dan bir eleman veren
hesaplama operasyonu bilineerdir.
- Haç çarpımı,
arasında bilineer bir eşleme teşkil eder.
Ayrıca bakınız
Dış bağlantılar
- Hazewinkel, Michiel, (Ed.) (2001), "Bilinear mapping", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Aralik 2019 Bilineer donusumler matematikte iki vektor uzayindan birer eleman alip ucuncu bir vektor uzayindan bir eleman veren ve bunu yaparken her iki girdi icin de dogrusallik aksiyomlarina uyan fonksiyonlardir TanimV1 V2 displaystyle V 1 V 2 ve W displaystyle W ayni K displaystyle mathbb K cismi uzerinde tanimli uc vektor uzayi olsun O zaman bir B V1 V2 W displaystyle B V 1 times V 2 mapsto W fonksiyonunun bilineer olmasi icin her v V2 displaystyle v in V 2 icin x B x v displaystyle x mapsto B x v eslemesinin ve her v V1 displaystyle v in V 1 icin de x B v x displaystyle x mapsto B v x eslemesinin ayri ayri dogrusal olmasi gerekir Diger bir degisle bir bilineer eslemenin iki girdisinden birisini sabitlemek her zaman bir lineer donusum verir Bu tanimla su ozellikler gecerli olur Her v1 V1 v2 V2 displaystyle v 1 in V 1 v 2 in V 2 ve her l K displaystyle lambda in mathbb K icin l displaystyle lambda yi B displaystyle B nin disina cekmek mumkundur yani B lv1 v2 lB v1 v2 B v1 lv2 displaystyle B lambda v 1 v 2 lambda B v 1 v 2 B v 1 lambda v 2 Her x1 x2 V1 v V2 displaystyle x 1 x 2 in V 1 v in V 2 icin B displaystyle B dagilma ozelligini gosterir yani B x1 x2 v B x1 v B x2 v displaystyle B x 1 x 2 v B x 1 v B x 2 v Ayni ozellik ikinci girdi icin de gecerlidir yani her v V1 x1 x2 V2 displaystyle v in V 1 x 1 x 2 in V 2 icin B v x1 x2 B v x1 B v x2 displaystyle B v x 1 x 2 B v x 1 B v x 2 gecerlidir Eger V1 displaystyle V 1 ve V2 displaystyle V 2 ayni V displaystyle V vektor uzayiysa ve ayni zamanda her v w V displaystyle v w in V icin B v w B w v displaystyle B v w B w v gecerliyse B displaystyle B ye simetrik denir Eger hedef W displaystyle W vektor uzayi K displaystyle mathbb K cismiyse de B displaystyle B ye bir bilineer form denir Mesela nokta carpimi simetrik bir bilineer formdur OzelliklerDogrusalligin geregi olarak eger v1 displaystyle v 1 veya v2 displaystyle v 2 vektorlerinden birisi 0 displaystyle mathbf 0 vektoruyse B v1 v2 0 displaystyle B v 1 v 2 mathbf 0 olur Tam tersi gecerli degildir v1 displaystyle v 1 ve v2 displaystyle v 2 vektorlerinin ikisi de sifirdan farkli olsa da B v1 v2 0 displaystyle B v 1 v 2 mathbf 0 olabilir B v1 v2 0 displaystyle B v 1 v 2 mathbf 0 ozelligini saglayan iki vektore ortogonal denir V1 displaystyle V 1 ve V2 displaystyle V 2 vektor uzaylarindan W displaystyle W ye olan tum bilineer formlar kendi aralarinda bir vektor uzayi teskil eder ve bu uzay Bil V1 V2 W displaystyle mathrm Bil V 1 V 2 W ile gosterilir Bu eger V1 V2 displaystyle V 1 V 2 ve W displaystyle W un ucu de sonlu boyutluysa Bil V1 V2 W displaystyle mathrm Bil V 1 V 2 W in boyutu bu uc vektor uzayinin boyutlarinin carpimina esittir OrneklerMatris carpimi Kk m Km n displaystyle mathbb K k times m times mathbb K m times n ile Kk n displaystyle mathbb K k times n arasinda bilineerdir Vektor ic carpimi bilineer bir donusumdur Girdileri ayni V displaystyle V vektor uzayindan olup ciktisi K displaystyle mathbb K dadir V displaystyle V ile V displaystyle V nin V displaystyle V dan iki eleman alip K displaystyle mathbb K dan bir eleman veren f v f v displaystyle f v mapsto f v hesaplama operasyonu bilineerdir Hac carpimi R3 R3 R3 displaystyle mathbb R 3 times mathbb R 3 mapsto mathbb R 3 arasinda bilineer bir esleme teskil eder Ayrica bakinizCokludogrusal haritaDis baglantilarHazewinkel Michiel Ed 2001 Bilinear mapping Encyclopaedia of Mathematics Kluwer Academic Publishers ISBN 978 1556080104
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State