Matematikte ve lineer cebirde bilineer form, bir vektör uzayından iki vektör alıp bir skaler veren bilineer fonksiyonlara denir. Başka bir değişle, bir cismi üzerinde tanımlı olan (mesela ) bir vektör uzayından iki eleman alıp 'dan bir eleman veren bir fonksiyonunun bilineer bir form olabilmesi için, iki elemanında da doğrusallık özelliklerini göstermesi gerekir:
- Her vektörleri ve her skaleri için 'yı 'nin dışına çekebilmek gerekir, yani olması gerekir.
- Her vektör üçlüsü için 'nin bir nevi dağılma özelliği göstermesi gerekir: ve
üzerinde tanımlı olan nokta çarpımı, bilineer formlara bir örnektir. Bunun dışında rölativitede kullanılan Minkowski çarpımı da bilineer formlara örnek verilebilir.
'nın karmaşık sayılar cismi olması hâlinde çoğu durumda bilineer formlardansa , yani argümanların birinde lineer, birinde yarı lineer (eşlenikli lineer) olan fonksiyonlar ilgimizi çekmektedir.
Tanımlar



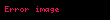




- Eğer her
ikilisi için
ilişkisi geçerli oluyorsa,
'ye simetrik bir bilineer form denir.
- Eğer her
vektörü için
ise,
'ye alternatif bir bilineer form denir.
- Eğer her
ikilisi için
ilişkisi geçerli oluyorsa,
'ye antisimetrik bir bilineer form denir. Eğer
ise, yani
cisminde
denemiyorsa (mesela
veya
üzerinde), o zaman alternatif olmakla antisimetrik olmak eşdeğerdir.
- Eğer sıfır hariç bir
vektörü için her
vektörüyle
veya
oluyorsa
'ye dejenere denir.
Ayrıca sözkonusu 


- Her
vektörü için
ise
'ye pozitif yarı belirli denir.
- Eğer
iken
ise
'ye pozitif belirli denir.
- Her
vektörü için
ise
'ye negatif yarı belirli denir.
- Eğer
iken
ise
'ye negatif belirli denir.
- Bazı
vektörleri için
oluyorken bazı
vektörleri için de
oluyorsa
'ye belirsiz denir.
Örnekler
üzerinde,
şeklinde tanımlanan nokta çarpımı, bir bilineer form teşkil eder.
- Özellikle kuantum fiziğinde çok kullanılan hilbert uzayında tanımlanan
şeklinde tanımlanan çarpım da bir bilineer form örneğidir. Burada söz konusu vektör uzayı sonsuz boyutludur.
Kordinat temsili
Martis temsili
Sonlu boyutlu vektör uzaylarında nasıl bir taban seçimiyle her lineer dönüşümün bir matris gösterimini elde etmek mümkünse aynı şey bilineer formlar için de mümkündür. 










Taban değişkliği
Lineer dönüşümlerde taban değişkliği formülü, 
Taban değişikliği altında yeni gösterimler, 



Özellikler
Refleksif (dönüşlü) bilineer formlar ve ortogonalite
Daha güçlü bir şart gözetmeden her 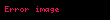




Refleksif bilineer formlar için bir ortogonalite (diklik) kavramı tanımlamak mümkündür. Öyle ki, 
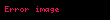


Benzer şekilde, herhangi bir 












Simetrik ve antisimetrik bilineer formlar







Seçilen her taban için simetrik bilineer formları temsil eden matrisler simetrik, ve antisimetrik bilineer formları temsil eden matrisler de antisimetrik olur.
Karesel form
Bir 







Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte ve lineer cebirde bilineer form bir vektor uzayindan iki vektor alip bir skaler veren bilineer fonksiyonlara denir Baska bir degisle bir K displaystyle mathbb K cismi uzerinde tanimli olan mesela R displaystyle mathbb R bir V displaystyle V vektor uzayindan iki eleman alip K displaystyle mathbb K dan bir eleman veren bir B displaystyle B fonksiyonunun bilineer bir form olabilmesi icin iki elemaninda da dogrusallik ozelliklerini gostermesi gerekir Her v w V displaystyle v w in V vektorleri ve her l K displaystyle lambda in mathbb K skaleri icin l displaystyle lambda yi B displaystyle B nin disina cekebilmek gerekir yani B lv w lB v w B v lw displaystyle B lambda v w lambda B v w B v lambda w olmasi gerekir Her v1 v2 w V displaystyle v 1 v 2 w in V vektor uclusu icin B displaystyle B nin bir nevi dagilma ozelligi gostermesi gerekir B v1 v2 w B v1 w B v2 w displaystyle B v 1 v 2 w B v 1 w B v 2 w ve B w v1 v2 B w v1 B w v2 displaystyle B w v 1 v 2 B w v 1 B w v 2 Rn displaystyle mathbb R n uzerinde tanimli olan nokta carpimi bilineer formlara bir ornektir Bunun disinda rolativitede kullanilan Minkowski carpimi da bilineer formlara ornek verilebilir K displaystyle mathbb K nin C displaystyle mathbb C karmasik sayilar cismi olmasi halinde cogu durumda bilineer formlardansa yani argumanlarin birinde lineer birinde yari lineer eslenikli lineer olan fonksiyonlar ilgimizi cekmektedir TanimlarV displaystyle V bir K displaystyle mathbb K vektor uzayi olsun Bir B V V K displaystyle B V times V mapsto mathbb K fonksiyonuna her v w V displaystyle v w in V icin hemv B v w displaystyle v mapsto B v w eslemesi hem dew B v w displaystyle w mapsto B v w eslemesi bir lineer fonksiyon teskil ediyorsa B displaystyle B ye bir bilineer form denir B displaystyle B eger ayriyeten baska birkac ozelligi de sagliyorsa basina birtakim sifatlar gelir Eger her v w V displaystyle v w in V ikilisi icin B v w B w v displaystyle B v w B w v iliskisi gecerli oluyorsa B displaystyle B ye simetrik bir bilineer form denir Eger her v V displaystyle v in V vektoru icin B v v 0 displaystyle B v v 0 ise B displaystyle B ye alternatif bir bilineer form denir Eger her v w V displaystyle v w in V ikilisi icin B v w B w v displaystyle B v w B w v iliskisi gecerli oluyorsa B displaystyle B ye antisimetrik bir bilineer form denir Eger char K 2 displaystyle mathrm char mathbb K neq 2 ise yani K displaystyle mathbb K cisminde 1 1 0 displaystyle 1 1 0 denemiyorsa mesela R displaystyle mathbb R veya C displaystyle mathbb C uzerinde o zaman alternatif olmakla antisimetrik olmak esdegerdir Eger sifir haric bir v V displaystyle v in V vektoru icin her x V displaystyle x in V vektoruyle B v x 0 displaystyle B v x 0 veya B x v 0 displaystyle B x v 0 oluyorsa B displaystyle B ye dejenere denir Ayrica sozkonusu K displaystyle mathbb K cismi R displaystyle mathbb R veya Q displaystyle mathbb Q gibi sirali bir cisim ise Her v V displaystyle v in V vektoru icin B v v 0 displaystyle B v v geq 0 ise B displaystyle B ye pozitif yari belirli denir Eger v 0 displaystyle v neq mathbb 0 iken B v v gt 0 displaystyle B v v gt 0 ise B displaystyle B ye pozitif belirli denir Her v V displaystyle v in V vektoru icin B v v 0 displaystyle B v v leq 0 ise B displaystyle B ye negatif yari belirli denir Eger v 0 displaystyle v neq mathbb 0 iken B v v lt 0 displaystyle B v v lt 0 ise B displaystyle B ye negatif belirli denir Bazi v V displaystyle v in V vektorleri icin B v v gt 0 displaystyle B v v gt 0 oluyorken bazi w V displaystyle w in V vektorleri icin de B w w lt 0 displaystyle B w w lt 0 oluyorsa B displaystyle B ye belirsiz denir OrneklerRn displaystyle mathbb R n uzerinde B v w k 1nvkwk displaystyle B v w sum k 1 n v k w k seklinde tanimlanan nokta carpimi bir bilineer form teskil eder Ozellikle kuantum fiziginde cok kullanilan hilbert uzayinda tanimlanan f g abf x g x dx displaystyle langle f g rangle int a b f x g x dx seklinde tanimlanan carpim da bir bilineer form ornegidir Burada soz konusu vektor uzayi sonsuz boyutludur Kordinat temsiliMartis temsili Sonlu boyutlu vektor uzaylarinda nasil bir taban secimiyle her lineer donusumun bir matris gosterimini elde etmek mumkunse ayni sey bilineer formlar icin de mumkundur B b1 b2 bn displaystyle mathcal B b 1 b 2 b n V displaystyle V nin bir tabani olsun O zaman her v V displaystyle v in V vektorunu v i 1nvibi displaystyle v sum i 1 n v i b i seklinde yazmak mumkundur Yani B v w displaystyle B v w u hesaplamak istiyorsak bunu B v w B i 1nvibi j 1nwjbj i 1nviB bi j 1nwjbj i j 1nviwjB bi bj displaystyle B v w B sum i 1 n v i b i sum j 1 n w j b j sum i 1 n v i B b i sum j 1 n w j b j sum i j 1 n v i w j B b i b j seklinde hesaplamamiz mumkundur Eger A Kn n displaystyle A in mathbb K n times n matrisini Aij B bi bj displaystyle A ij B b i b j seklinde tanimlarsak bu ifadeyiB v w i j 1nviwjB bi bj i j 1nviwjAij displaystyle B v w sum i j 1 n v i w j B b i b j sum i j 1 n v i w j A ij formuna getirebiliriz Sagda kalan ifade matris carpimi ile vTAw displaystyle v T Aw ifadesine esit oldugundan her bilineer formu bi taban secimiyle birlikte B v w vTAw displaystyle B v w v T Aw seklinde yazmak mumkundur Taban degiskligi Lineer donusumlerde taban degiskligi formulu SA S 1 A displaystyle SA S 1 A formuluyle veriliyordu Ancak bilineer formlarda taban degisikligi formulu biraz farklilik gosterir Taban degisikligi altinda yeni gosterimler v S 1v displaystyle v S 1 v seklinde bulundugundan v TA w vAw displaystyle v T A w vAw olmasini istiyorsak vTSTA Sw vTAw displaystyle v T S T A Sw v T Aw olmalidir Yani bilineer formlarda taban degisikligi icin STA S A displaystyle S T A S A formulu kullanilmaktadir Ayni lineer donusumu temsil eden matrislere benzer dendigi gibi ayni bilineer formu temsil eden matrislere de es denir OzelliklerRefleksif donuslu bilineer formlar ve ortogonalite Daha guclu bir sart gozetmeden her v w V displaystyle v w in V ikilisi icin eger B v w 0 displaystyle B v w 0 iliskisi ancak ve ancak B w v 0 displaystyle B w v 0 oldugunda gecerli oluyorsa B displaystyle B ye refleksif denir char K 2 displaystyle mathrm char mathbb K neq 2 olan cisimlerde her refleksif bilineer form ya simetrik ya da antisimetrik olmak zorundadir Refleksif bilineer formlar icin bir ortogonalite diklik kavrami tanimlamak mumkundur Oyle ki B v w 0 displaystyle B v w 0 veren her v w V displaystyle v w in V ciftine ortogonal veya dik denir ve bu durum v w displaystyle v perp w seklinde gosterilir Eger B displaystyle B nokta carpimi ise bu kavram oklid geometrisindeki diklik kavramiyla ortusmektedir Benzer sekilde herhangi bir U V displaystyle U leq V ve hatta herhangi bir altkume U V displaystyle U subseteq V icin ortogonal tamlayanini U v V B u v 0 u U displaystyle U perp v in V B u v 0 forall u in U olarak U displaystyle U daki tum vektorlere dik olan vektorler kumesi seklinde tanimlamak mumkundur Herhangi bir altkumenin ortogonal tamlayani bir altuzay teskil eder Vektor uzayindaki her vektore dik olan vektorlerin uzayina da V displaystyle V nin radikali denir ve bu altuzay da V displaystyle V perp ile gosterilir Eger B displaystyle B dejenere degilse V displaystyle V perp de trivial 0 displaystyle mathbf 0 uzayina esit olur U displaystyle U bir altuzaysa ve B displaystyle B dejenere degilse U displaystyle U perp icin boyut formulu gecerli olur dim U dim U dim V displaystyle dim U dim U perp dim V Refleksif olmayan bilineer formlar icin soldan ve sagdan diklik arasinda ayrim yapilmasi gerekmektedir Simetrik ve antisimetrik bilineer formlar B v w B w v displaystyle B v w B w v ozelligini saglayan bilineer formlara simetrik B v w B w v displaystyle B v w B w v ozelligini saglayanlara da antisimetrik denir Simetrik veya antisimetrik olmayan bilineer formlar icin eger char K 2 displaystyle mathrm char mathbb K neq 2 iseB v w 12 B v w B w v displaystyle B v w frac 1 2 B v w B w v veB v w 12 B v w B w v displaystyle B v w frac 1 2 B v w B w v seklinde bir simetrik ve bir de antisimetrik bilineer form tanimlamak mumkundur Bu durumda B v w B v w B v w displaystyle B v w B v w B v w oldugundan B displaystyle B yi biri simetrik biri antisimetrik iki parcaya ayirmis oluruz Secilen her taban icin simetrik bilineer formlari temsil eden matrisler simetrik ve antisimetrik bilineer formlari temsil eden matrisler de antisimetrik olur Karesel formBir B displaystyle B bilineer formu icin q v B v v displaystyle q v B v v seklinde tanimlanabilen fonksiyonlara karesel form denir char K 2 displaystyle mathrm char mathbb K neq 2 ise ve B displaystyle B simetrikse B displaystyle B yi q displaystyle q dan polarizasyon ozelligi ile cikarabiliriz B v w 12 q v w q v q w displaystyle B v w frac 1 2 q v w q v q w Simetrik olmayan bilineer formlar icin bu formul sadece simetrik kismi verir Antisimetrik bilineer formlar icin q v 0 displaystyle q v 0 olur Bu formulun baska bir sonucu ise simetrik bir bilineer formu tanimlamak icin sadece altinda yatan karesel formu tanimlamanin yetmesidir Ayrica bakinizBilineer fonksiyon Nokta carpimi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State