Grup (tutam veya öbek), soyut cebirin en temel matematiksel yapısıdır. Grup, ayrıca bir ikili işlemin tanımlı olduğu bir kümedir. Bir grubun grup olabilmesi için aynı zamanda bu işlemin birleşmeli, birim elemanlı ve olması gerekir. Soyut cebirin halka, cisim, modül gibi diğer yapılarının temelini oluşturur.
Gruplar, ilk başta geometrik şekillerin simetrilerini araştırırken keşfedilmiştir. Dolayısıyla bir kübün simetrileri, bir sonlu grup örneği olarak verilebilir. Ama aynı şekilde, tam sayıların kümesi de toplama işlemiyle birlikte bir grup teşkil eder.
Tanımlar ve Özellikler
Tanım
Eğer üzerinde bir tane 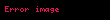

- Bileşme: Her
için
aksiyomunu sağlıyorsa bir yarı gruptur. Eğer bir yarı grup,
- Etkisiz eleman: Öyle bir
mevcuttur ki her
için
özelliğini sağlıyorsa bu kümeye monoid denir. Eğer bir monoid,
- : Her
için öyle bir
elemanı vardır ki
özelliğini de sağlıyorsa kümeye grup adı verilir. İşlemi vurgulamak için 
Ayrıca bir grup
- Değişme: Her
için
özelliğini de sağlıyorsa değişmeli grup ya da 'in anısına Abelyen grup olarak adlandırılır.
Özellikler
Yukarıdaki aksiyomlar sağlandığında bazı özellikler otomatikman geçerli olur:
- Etkisiz Elemanın Biricikliği Bir grupta birden fazla etkisiz eleman
bulunmaz.
- Ters Elemanların Biricikliği Her
elemanının yegâne bir ters elemanı
bulunur. Dolayısıyla elemanların tersini almak bir fonksiyondur ve bu fonksiyon şu özellikleri gösterir:
- Sadeleşme Özelliği
ise
- Bölme Özelliği Her
elemanları için
özelliğini sağlayan bir ve yegâne bir
mevcuttur.
- Üs n tane
'nın çarpımı kısaca
olarak gösterilir. Bu gösterim, aşağıdaki özellikleri sağlar
- Sadece abelyen gruplar için
Temel Kavramlar
Homomorfizma
İki grubun yapısındaki benzerliklere homomorfizma ismi verilir. Resmen tanımlamak gerekirse, 


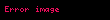




Bir homomorfizma için, 










Bir homomorfizma, aynı zamanda birebir ve örten ise bu homomorfizmaya izomorfizma adı verilir. Aralarında bir izomorfizma bulunan iki gruba izomorfik denir ve bu durum 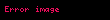
İzomorfizma örneği vermek gerekirse, 
Eğer 







Altgrup
Daha büyük bir grubun içinde bulunan gruplara altgrup ismi verilir. Resmen tanımlamak gerekirse, 






- Her
için
de
'nun içinde
- Her
elemanının tersi
'de
'nun içinde
boşküme değil
Bu iki şart sağlanınca diğer grup aksiyomları otomatikman kanıtlanır. Ayrıyeten, 
Örnek vermek gerekirse, tüm çift sayıların kümesi, tüm tam sayıların kümesinin bir altgrubudur. Benzer şekilde, bir karenin tüm rotasyon simetrileri, karenin tüm simetrilerinin grubunun bir altgrubudur.
Şimdi 








Eşkümeler
Şimdi 







Meselâ 






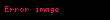
Grup çarpımı birebir olduğundan bir altgrubun tüm eşkümeleri eşit sayıda eleman içerir. Aynı zamanda, hiçbir eleman iki farklı eşkümenin aynı anda elemanı olamaz ve tüm eşkümelerin birleşimi de grubun tamamını verir. Bütün bunlar, Lagrange Teoremini kanıtlar: 



Abelyen olmayan gruplarda, hem soldan çarparak 



Bölüm Grupları
Eğer 













Örnek vermek gerekirse, 




Kaynakça
- Thomas W. Hungerford, Algebra, Springer-Verlag, Chapter I, 1974.
- Nathan Jacobson, Lectures in Abstract Algebra: I. Besic Concepts, Springer-Verlag, Chapter I, 1951.
- Serge Lang, Algebra, Addison-Wesley, 3. baskı, 1993.
- Yarasa Genel Müdürlüğü, Cebir, Hacettepe Üniversitesi FF, 2 cilt, 1987.
Ayrıca bakınız
 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Grup tutam veya obek soyut cebirin en temel matematiksel yapisidir Grup ayrica bir ikili islemin tanimli oldugu bir kumedir Bir grubun grup olabilmesi icin ayni zamanda bu islemin birlesmeli birim elemanli ve olmasi gerekir Soyut cebirin halka cisim modul gibi diger yapilarinin temelini olusturur Gruplar ilk basta geometrik sekillerin simetrilerini arastirirken kesfedilmistir Dolayisiyla bir kubun simetrileri bir sonlu grup ornegi olarak verilebilir Ama ayni sekilde tam sayilarin kumesi Z displaystyle mathbb mathbb Z de toplama islemiyle birlikte bir grup teskil eder Tanimlar ve OzelliklerTanim Eger uzerinde bir tane displaystyle ikili islemi tanimlanmis bir G displaystyle G kumesi Bilesme Her a b c G displaystyle a b c in G icin a b c a b c a b c displaystyle a b c a b c a b c aksiyomunu sagliyorsa bir yari gruptur Eger bir yari grup Etkisiz eleman Oyle bir e G displaystyle e in G mevcuttur ki her a G displaystyle a in G icin a e e a a displaystyle a e e a a ozelligini sagliyorsa bu kumeye monoid denir Eger bir monoid Her a G displaystyle a in G icin oyle bir a 1 G displaystyle a 1 in G elemani vardir ki a a 1 a 1 a e displaystyle a a 1 a 1 a e ozelligini de sagliyorsa kumeye grup adi verilir Islemi vurgulamak icin G displaystyle G gosterimi kullanilir Ayrica bir grup Degisme Her a b G displaystyle a b in G icin a b b a displaystyle a b b a ozelligini de sagliyorsa degismeli grup ya da in anisina Abelyen grup olarak adlandirilir Ozellikler Yukaridaki aksiyomlar saglandiginda bazi ozellikler otomatikman gecerli olur Etkisiz Elemanin Biricikligi Bir grupta birden fazla etkisiz eleman e displaystyle e bulunmaz Ters Elemanlarin Biricikligi Her a displaystyle a elemaninin yegane bir ters elemani a 1 displaystyle a 1 bulunur Dolayisiyla elemanlarin tersini almak bir fonksiyondur ve bu fonksiyon su ozellikleri gosterir ab 1 b 1a 1 displaystyle ab 1 b 1 a 1 e 1 e displaystyle e 1 e Sadelesme Ozelligi ab ac displaystyle ab ac ise b c displaystyle b c Bolme Ozelligi Her a b G displaystyle a b in G elemanlari icin b ac displaystyle b ac ozelligini saglayan bir ve yegane bir c displaystyle c mevcuttur Us n tane a a a displaystyle a a a nin carpimi kisaca an displaystyle a n olarak gosterilir Bu gosterim asagidaki ozellikleri saglar an 1 a 1 n a n displaystyle a n 1 a 1 n a n am n an m amn displaystyle a m n a n m a mn an am an m displaystyle a n a m a n m Sadece abelyen gruplar icin anbn ab n displaystyle a n b n ab n Temel KavramlarHomomorfizma Iki grubun yapisindaki benzerliklere homomorfizma ismi verilir Resmen tanimlamak gerekirse G displaystyle G ve H displaystyle H iki grup olsun ϕ G H displaystyle phi G mapsto H ise bu iki grup arasinda tanimli bir esleme olsun Eger her a b G displaystyle a b in G icin ϕ ab ϕ a ϕ b displaystyle phi ab phi a phi b ozelligi saglaniyorsa ϕ displaystyle phi ye bir homomorfizma denir Homomorfizmalar bize hem G displaystyle G hem de H displaystyle H nin yapisi hakkinda bilgi verdigi icin cok kullanislidir Bir homomorfizma icin imaj ϕ displaystyle mathrm imaj phi ile ϕ displaystyle phi nin goruntusu yani H displaystyle H de ϕ displaystyle phi ile ulasilabilen tum elemanlarin kumesi kastedilir imaj ϕ displaystyle mathrm imaj phi daima H displaystyle H nin bir altgrubudur ker ϕ displaystyle ker phi ile de ϕ displaystyle phi nin cekirdegi yani ϕ g e displaystyle phi g e ozelligini saglayan tum elemanlarin kumesi kastedilir ker ϕ displaystyle ker phi daima G displaystyle G nin bir altgrubudur hatta normal bir altgruptur Bir homomorfizma ayni zamanda birebir ve orten ise bu homomorfizmaya izomorfizma adi verilir Aralarinda bir izomorfizma bulunan iki gruba izomorfik denir ve bu durum G H displaystyle G cong H seklinde gosterilir Iki grubun izomorfik olmasi demek iki grubun tanim kumeleri farkli da olsa yapilarinin tamamen ayni olmasi demektir Grup teoresinde iki grubun birbiriyle ayni oldugu soylendiginde cogu zaman aslinda izomorfik oldugu kastedilir Izomorfizma ornegi vermek gerekirse ϕ x 2x displaystyle phi x mapsto 2x fonksiyonu tam sayilar ve cift tam sayilar arasinda bir izomorfizma teskil eder Dolayisiyla iki grubun tanim kumesi farkli olsa da belki sasirtici bir sekilde yapilarinin ayni oldugu ortaya cikar Eger ϕ G G displaystyle phi G mapsto G G displaystyle G nin elemanlarini yine G displaystyle G ye goturen bir homomorfizma ise ϕ displaystyle phi ye bir endomorfizma denir Eger ϕ displaystyle phi hem bir endomorfizma hem de bir izomorfizma ise ϕ displaystyle phi ye bir otomorfizma denir G displaystyle G nin tum otomorfizmalarini alip bir kumeye koyarsak bu otomorfizmalar kendi aralarinda bir grup teskil eder bu grup Aut G displaystyle mathrm Aut G ile gosterilir Altgrup Daha buyuk bir grubun icinde bulunan gruplara altgrup ismi verilir Resmen tanimlamak gerekirse U displaystyle U G displaystyle G nin bir altkumesi olsun Eger U displaystyle U G displaystyle G nin islemi ile kendi icinde de bir grupsa bu durumda U displaystyle U ya G displaystyle G nin altgrubu denir ve bu durum U G displaystyle U leq G seklinde gosterilir Bir grubun altgrup olup olmadigini kontrol etmek icin uc seye bakmak gerekir Her a b U displaystyle a b in U icin ab displaystyle ab de U displaystyle U nun icinde Her a displaystyle a elemaninin tersi a 1 displaystyle a 1 de U displaystyle U nun icinde U displaystyle U boskume degil Bu iki sart saglaninca diger grup aksiyomlari otomatikman kanitlanir Ayriyeten G displaystyle G nin eleman sayisi sonlu ise ikinci sart da otomatikman saglanir Ornek vermek gerekirse tum cift sayilarin kumesi tum tam sayilarin kumesinin bir altgrubudur Benzer sekilde bir karenin tum rotasyon simetrileri karenin tum simetrilerinin grubunun bir altgrubudur Simdi M displaystyle M G displaystyle G nin herhangi bir alt kumesi olsun M displaystyle M i iceren ve G displaystyle G nin tum altgruplarin kesisimine M displaystyle M tarafindan uretilen altgrup denir ve M displaystyle langle M rangle ile gosterilir Esdeger bir tanim ise M displaystyle M ve M displaystyle M deki elemanlarin toplamlari veya tersleri olarak yazilabilen tum elemanlarin olusturdugu altgruba M displaystyle langle M rangle denmesidir Eskumeler Simdi G displaystyle G bir grup U G displaystyle U leq G da bir altgrup olsun Bir g G displaystyle g in G secip U displaystyle U nun elemanlariyla tek tek carpip bunlari bir kumeye yerlestirirsek bu kumeye bir eskume denir ve bu gU displaystyle gU seklinde gosterilir Eskumeleri tanimlamanin baska bir yolu ise A displaystyle A bir eskume ise her a b A displaystyle a b in A icinab 1 U displaystyle ab 1 in U olmasini gerektirmektir Mesela G displaystyle G yi bir karenin simetrileri olarak alirsak ve karenin rotasyon simetrilerinden olusan altgrubunu ise U displaystyle U ile gosterirsek G displaystyle G iki eskumeye bolunur U displaystyle U nun kendisi ve bir yansitmadan sonra ulasilabilen simetrilerin kumesi Veya Z displaystyle mathbb Z yi alip 3 un katlarini iceren altgruba bolersek 3 eskume elde ederiz 6 3 0 3 6 displaystyle 6 3 0 3 6 5 2 1 4 7 displaystyle 5 2 1 4 7 4 1 2 5 7 displaystyle 4 1 2 5 7 Grup carpimi birebir oldugundan bir altgrubun tum eskumeleri esit sayida eleman icerir Ayni zamanda hicbir eleman iki farkli eskumenin ayni anda elemani olamaz ve tum eskumelerin birlesimi de grubun tamamini verir Butun bunlar Lagrange Teoremini kanitlar U G displaystyle U leq G ise ve G displaystyle G sonluysa U displaystyle U nun eleman sayisi G displaystyle G nin eleman sayisinin daima bir bolenidir Abelyen olmayan gruplarda hem soldan carparak gU displaystyle gU seklinde hem de sagdan carparak Ug displaystyle Ug seklinde eskumeler elde etmek mumkundur Bu eskumelerin birbirinin aynisi olmasi da zorunlu degildir ancak ayni oldugu durumlarda U displaystyle U ya bir normal altgrup denir ve bu durum U G displaystyle U trianglelefteq G seklinde gosterilir Abelyen gruplarin tum altgruplari normaldir Bolum Gruplari Eger U displaystyle U G displaystyle G nin normal bir altgrubuysa U displaystyle U nun eskumeleri arasinda bir islem tanimlamak mumkundur Cunku sadece U displaystyle U normalse U displaystyle U nun iki eskumesi A displaystyle A ve B displaystyle B den iki eleman alip carpinca yine tek bir eskumeye ait elemanlar elde ederiz U displaystyle U normal bir altgrup degilse sectigimiz elemana gore farkli eskumeler elde etmek mumkundur U displaystyle U nun eskumeleri arasinda bu sekilde bir islem tanimlayip elde ettigimiz gruba U displaystyle U nun bolum grubu denir ve bu G U displaystyle G U ile gosterilir Bu sekilde G displaystyle G yi daha basit olan iki parcaya ayirmis oluruz U displaystyle U ve G U displaystyle G U Ornek vermek gerekirse G displaystyle G yi karenin simetri grubu olarak aldigimizda sadece rotasyon simetrilerini iceren altgrup U displaystyle U normaldir Bu durumda G U displaystyle G U iki elemandan olusan bir altgrup verir ve 8 elemanli G displaystyle G yi 4 ve 2 elemanli iki grup olarak parcalamis oluruz Ayni sekilde tum tam sayilari alip 5 in katlarina bolersek 5 elemanli bir grup elde etmis oluruz Bu bolum grubu 0 1 2 3 4 displaystyle 0 1 2 3 4 sayilarinin modulo 5 toplandigi gruba izomorftur KaynakcaThomas W Hungerford Algebra Springer Verlag Chapter I 1974 Nathan Jacobson Lectures in Abstract Algebra I Besic Concepts Springer Verlag Chapter I 1951 Serge Lang Algebra Addison Wesley 3 baski 1993 Yarasa Genel Mudurlugu Cebir Hacettepe Universitesi FF 2 cilt 1987 Ayrica bakinizCisim HalkaMatematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State