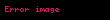Cauchy yakınsaklık testi, sonsuz serilerin yakınsaklığını bulmak için kullanılan test yöntemlerinden birisidir. Bu yakınsama ölçütü, bu yöntemi 1821'de yazdığı Cours d'Analyse adlı ders kitabında yayınlayan Augustin-Louis Cauchy'nin adını taşımaktadır.
İfade

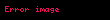
olan tüm
'ler ve
için
önermesini sağlayan bir N
Açıklama
Bu testin geçerli olmasının sebebi 


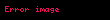

Serilerin tam metrik uzaylardaki yakınsaklığının Cauchy dizisi tanımına taşınabilmesinin altında yatan gerçek metrik uzaylarda bütün Cauchy dizilerinin aslında yakınsak olduğudur.
Ayrıca bakınız
Kaynakça
- ^ Abbott, Stephen (2001). Understanding analysis. Undergraduate Texts in Mathematics. New York, NY: Springer Verlag. s. 63. ISBN .
Bu makale PlanetMath'deki Yakınsaklık için Cauchy ölçütü maddesinden lisansıyla faydalanmaktadır.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Cauchy yakinsaklik testi sonsuz serilerin yakinsakligini bulmak icin kullanilan test yontemlerinden birisidir Bu yakinsama olcutu bu yontemi 1821 de yazdigi Cours d Analyse adli ders kitabinda yayinlayan Augustin Louis Cauchy nin adini tasimaktadir Ifade i 0 ai displaystyle sum i 0 infty a i serisinin yakinsakligi ancak ve ancak her e gt 0 displaystyle varepsilon gt 0 icin n gt N displaystyle n gt N olan tum n displaystyle n ler ve p 1 displaystyle p geq 1 icin an 1 an 2 an p lt e displaystyle a n 1 a n 2 cdots a n p lt varepsilon onermesini saglayan bir N N displaystyle in mathbb N sayisi varsa mumkundur AciklamaBu testin gecerli olmasinin sebebi R displaystyle mathbb R veya C displaystyle mathbb C gibi uzaylarin tam metrik uzay olmasidir Cunku metrik uzay baglaminda serilerin yakinsakligi ancak ve ancak kismi toplamlarin yani sn i 0nai displaystyle s n sum i 0 n a i dizilerinin bir Cauchy dizisi olmasiyla mukundur Burada bahsedilen Cauchy dizisinin tanimi ise sudur Her e gt 0 displaystyle varepsilon gt 0 icin bir N sayisi vardir oyle ki her n m gt N icin sm sn lt e displaystyle s m s n lt varepsilon saglanir Serilerin tam metrik uzaylardaki yakinsakliginin Cauchy dizisi tanimina tasinabilmesinin altinda yatan gercek metrik uzaylarda butun Cauchy dizilerinin aslinda yakinsak oldugudur Ayrica bakinizSeri matematik Kaynakca Abbott Stephen 2001 Understanding analysis Undergraduate Texts in Mathematics New York NY Springer Verlag s 63 ISBN 978 0 387 21506 8 Bu makale PlanetMath deki Yakinsaklik icin Cauchy olcutu maddesinden GFDL lisansiyla faydalanmaktadir
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans