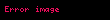Matematiksel analizde, M metrik uzay olmak üzere, elemanları M 'de olan her Cauchy dizisinin yine M'de bir limiti varsa,veya alternatif olarak, M'deki her Cauchy dizisi yine M'de yakınsaksa M metrik uzayına tam (veya Cauchy uzayı) denir.
Sezgisel olarak, bir uzay içinde veya sınırlarında eksik bir nokta yoksa tamdır. Örneğin, rasyonel sayılar kümesi tam değildir, çünkü her ne kadar 'ye yakınsayan rasyonel sayılardan oluşan bir Cauchy dizisi oluşturulabilse de bu nokta uzayda eksiktir (aşağıdaki diğer örneklere bakınız). Aşağıda açıklandığı gibi verilen bir uzayı tamlaştırılmak için "tüm delikleri doldurmak" her zaman mümkündür.
Örnekler
Rasyonel sayılar uzayı 

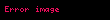


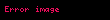

Yine mutlak değer metriğiyle 


Reel sayılar uzayı 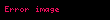



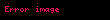


P -sel sayıların uzayı 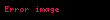



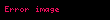





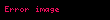





Bazı teoremler
X metrik uzayının tam olması için gerek ve yeter koşul, X’in boş olmayan kapalı alt kümelerinin, çapları 0'a yakınsayan, her azalan dizisinin arakesitinin boş kümeden farklı olmasıdır: Fn kapalı ve boş olmayan küme, her n için Fn+1 ⊆ Fn ve diam(Fn) → 0 ise o zaman tüm Fn kümelerinde ortak bir x ∈ X noktası vardır.
Her kompakt metrik uzay tamdır, ancak her tam uzay kompakt olmayabilir. Aslında, bir metrik uzayın kompakt olması için gerek ve yeter koşul tam ve tamamen sınırlı olmasıdır. Bu ifade, 

(X, d) tam bir metrik uzay olsun. A ⊆ X kapalı ise, A aynı zamanda tamdır.(X, d) metrik bir uzay olsun. A ⊆ X tam bir alt uzaysa, A kapalıdır.
X bir küme ve M bir tam metrik uzay olmak üzere, 



X bir topolojik uzay ve M bir tam metrik uzay ise, '


Baire kategori teoremi, her tam metrik uzayın bir Baire uzayı olduğunu ifade eder. Yani, bu uzayın hiçbir yerde yoğun olmayan alt kümeleri sayılabilir birleşiminin içi boştur.
Banach sabit nokta teoremi, tam metrik uzaydaki bir daraltan(büzülme) dönüşümün sadece ve sadece bir tek sabit noktaya sahip olduğunu belirtir. Bu sabit nokta teoremi genellikle Banach uzayları gibi tam metrik uzaylarda ters fonksiyon teoremini kanıtlamak için kullanılır.
Bir metrik uzayın genişleme sabiti, tüm 

kesişimi boştan farklı olur. Bir metrik uzay ancak ve ancak genişleme sabiti 2'den küçükse tamdır.
Tamlaştırma
Herhangi bir 



Kaynakça
- ^ Introduction to Metric and Topological Spaces. ISBN .
- ^ "Archived copy". 30 Haziran 2007 tarihinde kaynağından . Erişim tarihi: 14 Ocak 2007.
- ^ "Archived copy". 30 Haziran 2007 tarihinde kaynağından . Erişim tarihi: 14 Ocak 2007.
- ^ Grünbaum (1960). "Some applications of expansion constants". 10 (1). ss. 193-201. 4 Mart 2016 tarihinde kaynağından . Erişim tarihi: 12 Mayıs 2020.
Bibliyografya
- Kelley, John L. (1975). General Topology (İngilizce). Springer. ISBN .
- Kreyszig, Erwin, Introductory functional analysis with applications (Wiley, New York, 1978).
- Lang, Serge, "Real and Functional Analysis"
- Meise, Reinhold; Vogt, Dietmar (1997). Introduction to functional analysis. Ramanujan, M.S. (trans.). Oxford: Clarendon Press; New York: Oxford University Press. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematiksel analizde M metrik uzay olmak uzere elemanlari M de olan her Cauchy dizisinin yine M de bir limiti varsa veya alternatif olarak M deki her Cauchy dizisi yine M de yakinsaksa M metrik uzayina tam veya Cauchy uzayi denir Sezgisel olarak bir uzay icinde veya sinirlarinda eksik bir nokta yoksa tamdir Ornegin rasyonel sayilar kumesi tam degildir cunku her ne kadar 2 displaystyle sqrt 2 ye yakinsayan rasyonel sayilardan olusan bir Cauchy dizisi olusturulabilse de bu nokta uzayda eksiktir asagidaki diger orneklere bakiniz Asagida aciklandigi gibi verilen bir uzayi tamlastirilmak icin tum delikleri doldurmak her zaman mumkundur OrneklerRasyonel sayilar uzayi Q displaystyle scriptstyle mathbb Q farkin mutlak degeri olarak tanimlanan standart metrik ile tam degildir Ornegin x1 1 textstyle x 1 1 ve xn 1 xn2 1xn textstyle x n 1 frac x n 2 frac 1 x n seklinde verilen dizi goz onune alinsin Bu rasyonel sayilardan olusan bir Cauchy dizisidir ancak herhangi bir rasyonel bir limite yakinsamaz Eger bu dizinin limiti var ve limit x displaystyle x ise o zaman x x2 1x textstyle x frac x 2 frac 1 x esitliginden x2 2 textstyle x 2 2 bulunur ki hicbir rasyonel sayi bu ozelligi tasimaz Bununla birlikte ayni dizi gercek sayilarin bir dizisi olarak kabul edilirse 2 displaystyle sqrt 2 irrasyonel sayisina yakinsar Yine mutlak deger metrigiyle 0 1 displaystyle 0 1 acik araligi da tam degildir xn 1n displaystyle x n frac 1 n ile tanimlanan dizi Cauchy dizisidir fakat verilen uzayda bir limiti yoktur Ancak 0 1 displaystyle 0 1 kapali araligi tamdir ornegin verilen dizinin bu aralikta bir limiti vardir ve bu limit sifirdir Reel sayilar uzayi R displaystyle scriptstyle mathbb R ve karmasik sayilar uzayi C displaystyle scriptstyle mathbb C mutlak deger yardimiyla olusturulan metrikle tamdir ve bu nedenle Oklit uzaklik metrigi ile verilen Oklid uzayi Rn displaystyle scriptstyle mathbb R n de tamdir Buna karsilik sonsuz boyutlu normlu vektor uzaylari tam olabilir de olmayabilir de tam olanlari Banach uzaylaridir Kapali ve sinirli bir aralikta surekli reel degerli fonksiyonlarin uzayi C a b displaystyle C a b bir Banach uzayidir ve dolayisiyla supremum normuna gore tam bir metrik uzaydir Ancak supremum normu a b displaystyle a b araligindaki surekli fonksiyonlar uzayi C a b displaystyle C a b uzerinde bir norm olusturmaz cunku sinirsiz fonksiyonlar icerir Bunun yerine kompakt yakinsamanin topolojisi ile C a b displaystyle C a b uzayina bir Frechet uzayi yapisi verilebilir bu uzay uzerindeki topoloji oteleme donusumu altinda degismeyen tam bir metrik ile olusturulabilen lokal konveks bir topolojik vektor uzayidir P sel sayilarin uzayi Qp displaystyle scriptstyle mathbb Q p herhangi bir p displaystyle p asal sayisi icin tamdir Bu uzay p displaystyle p sel metrigiyle Q displaystyle scriptstyle mathbb Q yu tipki R displaystyle scriptstyle mathbb R nin Q displaystyle scriptstyle mathbb Q yu normal metrikle tamamladigi gibi tamamlar S displaystyle S keyfi bir kume olmak uzere S displaystyle S kumesi uzerindeki tum dizilerin kumesi SN displaystyle S N tam metrik uzaydir Gercekten xn displaystyle x n ve yn displaystyle y n dizileri arasindaki uzakligi xN displaystyle x N ile yN displaystyle y N yi farkli yapan en kucuk indis N displaystyle N olmak uzere 1 N boyle bir indis yoksa 0 displaystyle 0 olarak tanimlanirsa gorulebilir Bu uzay S displaystyle S ayrik uzayinin sayilabilir sayida kopyasinin carpimi ile homeomorftur Bazi teoremlerX metrik uzayinin tam olmasi icin gerek ve yeter kosul X in bos olmayan kapali alt kumelerinin caplari 0 a yakinsayan her azalan dizisinin arakesitinin bos kumeden farkli olmasidir Fn kapali ve bos olmayan kume her n icin Fn 1 Fn ve diam Fn 0 ise o zaman tum Fn kumelerinde ortak bir x X noktasi vardir Her kompakt metrik uzay tamdir ancak her tam uzay kompakt olmayabilir Aslinda bir metrik uzayin kompakt olmasi icin gerek ve yeter kosul tam ve tamamen sinirli olmasidir Bu ifade Rn displaystyle scriptstyle mathbb R n Rn displaystyle scriptstyle mathbb R n nin herhangi bir kapali ve sinirli S displaystyle S alt uzayi kompakt dolayisiyla tam oldugunu ifade eden Heine Borel teoreminin bir genellemesidir X d tam bir metrik uzay olsun A X kapali ise A ayni zamanda tamdir X d metrik bir uzay olsun A X tam bir alt uzaysa A kapalidir X bir kume ve M bir tam metrik uzay olmak uzere X displaystyle X ten M displaystyle M ye giden tum sinirli lt i id mwmg gt f lt i gt fonksiyonlarin kumesi B X M displaystyle B X M bir tam metrik uzaydir Burada B X M displaystyle B X M dek uzaklik fonksiyonunu supremum normu ile M deki metrik cinsinden soyledir d f g sup d f x g x x X displaystyle d f g equiv sup left d f x g x x in X right X bir topolojik uzay ve M bir tam metrik uzay ise X displaystyle X ten M displaystyle M ye surekli ve sinirliffonksiyonlarin kumesi Cb X M displaystyle C b X M B X M displaystyle B X M nin kapali bir alt uzayidir ve boylece tamdir Baire kategori teoremi her tam metrik uzayin bir Baire uzayi oldugunu ifade eder Yani bu uzayin hicbir yerde yogun olmayan alt kumeleri sayilabilir birlesiminin ici bostur Banach sabit nokta teoremi tam metrik uzaydaki bir daraltan buzulme donusumun sadece ve sadece bir tek sabit noktaya sahip oldugunu belirtir Bu sabit nokta teoremi genellikle Banach uzaylari gibi tam metrik uzaylarda ters fonksiyon teoremini kanitlamak icin kullanilir Bir metrik uzayin genisleme sabiti tum m displaystyle textstyle mu sabitlerin infimumudur oyle ki B xa ra displaystyle textstyle left overline B x alpha r alpha right ailesi ikiserli olarak kesistiginde aB xa mra displaystyle bigcap alpha overline B x alpha mu r alpha kesisimi bostan farkli olur Bir metrik uzay ancak ve ancak genisleme sabiti 2 den kucukse tamdir TamlastirmaHerhangi bir M displaystyle M metrik uzayi icin M displaystyle M yi yogun alt uzay olarak ihtiva eden bir M displaystyle M prime veya M displaystyle overline M ile de gosterilir tam metrik uzay elde edilebilir Bu uzay asagidaki evrensel ozellige sahiptir N herhangi bir tam metrik alan ve on herhangi biri olup olmadigini duzgun surekli fonksiyon N M daha sonra vardir benzersiz f uzanan N M duzgun surekli fonksiyonf M boslugu bu ozellik tarafindan izometriye kadar belirlenir izometrik olarak M iceren tum tam metrik uzaylar arasinda ve M nin tamamlanmasi olarak adlandirilir Kaynakca Introduction to Metric and Topological Spaces ISBN 978 0 19 853161 6 Archived copy 30 Haziran 2007 tarihinde kaynagindan Erisim tarihi 14 Ocak 2007 Archived copy 30 Haziran 2007 tarihinde kaynagindan Erisim tarihi 14 Ocak 2007 Grunbaum 1960 Some applications of expansion constants 10 1 ss 193 201 4 Mart 2016 tarihinde kaynagindan Erisim tarihi 12 Mayis 2020 BibliyografyaKelley John L 1975 General Topology Ingilizce Springer ISBN 0 387 90125 6 Kreyszig Erwin Introductory functional analysis with applications Wiley New York 1978 0 471 03729 X Lang Serge Real and Functional Analysis 0 387 94001 4 Meise Reinhold Vogt Dietmar 1997 Introduction to functional analysis Ramanujan M S trans Oxford Clarendon Press New York Oxford University Press ISBN 0 19 851485 9
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans