Matematikte, bir düzlem eğrisi veya düzlemsel eğri, bir düzlem içinde yer alan (yani tüm noktaları düzlem içinde kalan) bir eğri olup söz konusu düzlem, bir Öklid düzlemi, bir veya bir olabilir. En sık çalışılan durumlar, düzgün düzlem eğrileri (parçalı düzgün düzlem eğrileri dahil) ve .

Düzlem eğrileri ayrıca (düzlemin bir bölgesini çevreleyen ancak düzgün olması gerekmeyen eğriler) ve sürekli fonksiyonların grafiklerini de içerir.
Sembolik gösterim
Bir düzlem eğrisi genellikle Kartezyen koordinatlarda belirli bir f fonksiyonu için 





Düzlem eğrileri bazen her noktanın konumunu bir açı ve orijinden uzaklık cinsinden ifade eden kutupsal koordinatlar gibi alternatif koordinat sistemi ile de gösterilebilir.
Düzgün düzlem eğrisi
Düzgün düzlem eğrisi, gerçel 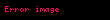
Eşdeğer olarak, düzgün bir düzlem eğrisi yerel olarak 


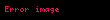
Cebirsel düzlem eğrisi
, bir polinom denklemi 

Cebirsel eğriler, 18. yüzyıldan beri kapsamlı bir şekilde çalışılmaktadır.
Her cebirsel düzlem eğrisinin bir derecesi vardır, tanımlayıcı denklemin , bir olması durumunda, eğrinin bir doğruyla kesişme sayısına eşittir. Örneğin, 
Derecesi 2 olan düzlem cebirsel eğrilere konik kesitler denir ve bunların 

Örnekler
Çok sayıda düzlem eğrisi örneği Eğriler galerisinde gösterilmiş ve Eğriler listesinde listelenmiştir. Derecesi 1 veya 2 olan cebirsel eğriler burada gösterilmektedir (derecesi 3'ten küçük olan cebirsel eğriler her zaman bir düzlem içinde yer alır):
| Ad | Parametrik denklem | Bir fonksiyon olarak | grafik | |
|---|---|---|---|---|
| Düz çizgi | 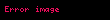 |  |  |  |
| Çember |  |  |  | |
| Parabol |  |  |  |  |
| Elips |  |  |  | |
| Hiperbol |  |  |  |
Ayrıca bakınız
Kaynakça
Dış bağlantılar
- Eric W. Weisstein, Plane Curve (MathWorld)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte bir duzlem egrisi veya duzlemsel egri bir duzlem icinde yer alan yani tum noktalari duzlem icinde kalan bir egri olup soz konusu duzlem bir Oklid duzlemi bir veya bir olabilir En sik calisilan durumlar duzgun duzlem egrileri parcali duzgun duzlem egrileri dahil ve Bir Hipotrokoid Deltoid animasyonu Duzlem egrileri ayrica duzlemin bir bolgesini cevreleyen ancak duzgun olmasi gerekmeyen egriler ve surekli fonksiyonlarin grafiklerini de icerir Sembolik gosterimBir duzlem egrisi genellikle Kartezyen koordinatlarda belirli bir f fonksiyonu icin f x y 0 displaystyle f x y 0 seklinde bir ile temsil edilebilir Bu denklem y veya x icin acik bir sekilde cozulebilirse yani belirli bir g veya h fonksiyonu icin y g x displaystyle y g x veya x h y displaystyle x h y olarak yeniden yazilabilirse bu temsilin alternatif acik bir bicimini saglar Bir duzlem egrisi genellikle Kartezyen koordinatlarda belirli x t displaystyle x t ve y t displaystyle y t fonksiyonlari icin x y x t y t displaystyle x y x t y t bicimindeki bir parametrik denklem ile de gosterilebilir Duzlem egrileri bazen her noktanin konumunu bir aci ve orijinden uzaklik cinsinden ifade eden kutupsal koordinatlar gibi alternatif koordinat sistemi ile de gosterilebilir Duzgun duzlem egrisiDuzgun duzlem egrisi gercel R2 displaystyle mathbb R 2 Oklid duzlemi icinde bir egridir ve tek boyutlu bir Bu duzgun bir duzlem egrisinin yerel olarak bir dogru gibi gorunen bir duzlem egrisi oldugu anlamina gelir yani her noktanin yakininda bir duzgun fonksiyon tarafindan bir dogruya eslenebilir Esdeger olarak duzgun bir duzlem egrisi yerel olarak f x y 0 displaystyle f x y 0 denklemiyle verilebilir burada f R2 R displaystyle f mathbb R 2 to mathbb R bir duzgun fonksiyondur ve f x displaystyle partial f partial x ile f y displaystyle partial f partial y kismi turevleri egrinin bir noktasinda asla her ikisi birlikte 0 degildir Cebirsel duzlem egrisi bir polinom denklemi f x y 0 displaystyle f x y 0 veya F x y z 0 displaystyle F x y z 0 ile verilen veya icindeki bir egridir burada F projektif durumda bir Cebirsel egriler 18 yuzyildan beri kapsamli bir sekilde calisilmaktadir Her cebirsel duzlem egrisinin bir derecesi vardir tanimlayici denklemin bir olmasi durumunda egrinin bir dogruyla kesisme sayisina esittir Ornegin x2 y2 1 displaystyle x 2 y 2 1 denklemiyle verilen dairenin derecesi 2 dir Derecesi 2 olan duzlem cebirsel egrilere konik kesitler denir ve bunlarin x2 y2 1 displaystyle x 2 y 2 1 cemberinin izdusumsel tamamlanmasiyla izomorfiktir yani x2 y2 z2 0 displaystyle x 2 y 2 z 2 0 denkleminin izdusumsel egrisi Derecesi 3 olan duzlem egrilere ve eger tekil degillerse denir Derecesi 4 olanlar olarak adlandirilir OrneklerCok sayida duzlem egrisi ornegi Egriler galerisinde gosterilmis ve Egriler listesinde listelenmistir Derecesi 1 veya 2 olan cebirsel egriler burada gosterilmektedir derecesi 3 ten kucuk olan cebirsel egriler her zaman bir duzlem icinde yer alir Ad Parametrik denklem Bir fonksiyon olarak grafikDuz cizgi ax by c displaystyle ax by c x y x0 at y0 bt displaystyle x y x 0 alpha t y 0 beta t y mx c displaystyle y mx c Cember x2 y2 r2 displaystyle x 2 y 2 r 2 x y rcos t rsin t displaystyle x y r cos t r sin t Parabol y x2 0 displaystyle y x 2 0 x y t t2 displaystyle x y t t 2 y x2 displaystyle y x 2 Elips x2a2 y2b2 1 displaystyle frac x 2 a 2 frac y 2 b 2 1 x y acos t bsin t displaystyle x y a cos t b sin t Hiperbol x2a2 y2b2 1 displaystyle frac x 2 a 2 frac y 2 b 2 1 x y acosh t bsinh t displaystyle x y a cosh t b sinh t Ayrica bakinizCebirsel geometri Diferansiyel geometri Duzlem egrisi uydurmaKaynakcaCoolidge J L 28 Nisan 2004 A Treatise on Algebraic Plane Curves Dover Publications ISBN 0 486 49576 0 Yates R C 1952 A handbook on curves and their properties J W Edwards ASIN B0007EKXV0 Lawrence J Dennis 1972 A catalog of special plane curves Dover ISBN 0 486 60288 5 Dis baglantilarEric W Weisstein Plane Curve MathWorld
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans
