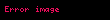Matematikte, bir parametrik denklem, bir grup niceliği parametreler olarak adlandırılan bir veya daha fazla bağımsız değişkenin fonksiyonları olarak tanımlar. Parametrik denklemler genellikle bir eğri veya gibi geometrik bir nesneyi oluşturan noktaların koordinatlarını ifade etmek için kullanılır ve sırasıyla parametrik eğri ve parametrik yüzey olarak adlandırılır. Bu gibi durumlarda, denklemler, toplu olarak nesnenin parametrik temsili veya parametrik sistem, veya parametrelendirilmesi (alternatif olarak parametrelendirme olarak yazılır) olarak adlandırılır.

Örneğin,
denklemleri, t parametre olmak üzere birim çemberin parametrik bir temsilini oluşturur: Bir nokta (x, y) birim çember üzerindedir ancak ve ancak t değeri varsa bu iki denklem o noktayı oluşturur. Bazen skaler çıktı değişkenleri için parametrik denklemler vektörler içinde tek bir parametrik denklemde birleştirilir:
Parametrik gösterimler genellikle benzersiz değildir (aşağıdaki "İki boyutta örnekler" bölümüne bakın), bu nedenle aynı büyüklükler bir dizi farklı parametrelendirme ile ifade edilebilir.
Eğriler ve yüzeylere ek olarak parametrik denklemler, parametre sayısı manifoldun veya varyetenin boyutuna eşit olacak şekilde, daha yüksek (boyutu) olan manifoldları ve cebirsel varyeteleri tanımlayabilir ve denklem sayısı manifold veya varyetenin göz önünde bulundurulduğu uzayın boyutuna eşittir (eğriler için boyut "bir" ve "bir" parametre kullanılır, yüzeyler için boyut "iki" ve "iki" parametre vb. ).
Parametrik denklemler genellikle kinematik alanında kullanılır; burada bir nesnenin yörüngesi parametre olarak zamana bağlı denklemlerle temsil edilir. Bu uygulama nedeniyle, tek bir parametre genellikle t olarak etiketlenir; ancak, parametreler diğer fiziksel büyüklükleri (geometrik değişkenler gibi) temsil edebilir veya kolaylık sağlamak için keyfi olarak seçilebilir. Parametrelendirmeler benzersiz ve tek değildir; birden fazla parametrik denklem kümesi aynı eğriyi belirtebilir.
Uygulamaları
Kinematik
Kinematikte, nesnelerin uzaydaki yolları genellikle parametrik eğriler olarak tanımlanır ve her bir uzaysal koordinat açıkça bağımsız bir parametreye (genellikle zaman) bağlıdır. Bu şekilde kullanıldığında, nesnenin koordinatları için parametrik denklemler kümesi toplu olarak konum için bir vektör-değerli fonksiyon oluşturur. Bu tür parametrik eğriler daha sonra terimsel olarak integrallenebilir ve türevlenebilir olabilir. Böylece, bir parçacığın konumu parametrik olarak şöyle tanımlanırsa

o zaman hız şu şekilde;

ve ivme de aşağıdaki gibi bulunabilir

Bilgisayar destekli tasarım
Parametrik denklemlerin bir diğer önemli kullanımı bilgisayar destekli tasarım (CAD) alanındadır. Örneğin, hepsi düzlemsel eğrileri tanımlamak için yaygın olarak kullanılan aşağıdaki üç gösterimi inceleyin.
| Tür | Biçim | Örnek | Tanım |
|---|---|---|---|
| Açık |  |  | Doğru |
| Örtük |  |  | Çember |
| Parametrik |   | 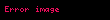  | Doğru |
  | Çember |
Her bir gösterimin CAD uygulamaları için avantajları ve dezavantajları vardır.
Açık gösterim çok karmaşık olabilir, hatta mevcut olmayabilir. Dahası, ve özellikle de altında iyi sonuç vermez. Öte yandan, parametrik bir denklem ve örtük bir denklem açık bir gösterimden kolayca çıkarılabileceğinden, basit bir açık gösterim mevcut olduğunda, diğer iki gösterimin avantajlarına sahiptir.
Örtük gösterimler eğri üzerinde noktalar oluşturmayı ve hatta gerçek noktalar olup olmadığına karar vermeyi zorlaştırabilir. Öte yandan, verilen bir noktanın bir eğri üzerinde olup olmadığına veya kapalı bir eğrinin içinde mi yoksa dışında mı olduğuna karar vermek için çok uygundurlar.
Bu tür kararlar parametrik bir gösterimle zor olabilir, ancak parametrik gösterimler bir eğri üzerinde noktalar oluşturmak ve bunu çizmek için en uygun olanıdır.
Tam sayı geometrisi
alanındaki çok sayıda problem parametrik denklemler kullanılarak çözülebilir. Bu tür klasik bir çözüm Öklid'in dik üçgenleri, kenarlarının a, b ve hipotenüslerinin c uzunlukları aralarında asal tam sayılar olacak şekilde parametrize etmesidir. a ve b çift olmadığından (aksi takdirde a, b ve c çift olmazdı), a çift olacak şekilde değiştirilebilir ve parametrelendirme şu şekilde olur:

burada m ve n parametreleri her ikisi de tek olmayan pozitif aralarında asal tam sayılardır.
a, b ve c'yi rastgele bir pozitif tam sayı ile çarparak, üç kenarı tam sayı uzunluğunda olan tüm dik üçgenlerin parametrizasyonunu elde ederiz.
Örtükleştirme
Bir dizi parametrik denklemin tek bir dönüştürülmesi, t değişkeninin eşzamanlı 





Eğer parametrizasyon,

tarafından veriliyorsa bir hesaplaması örtükleştirmeye izin verir, burada p, q ve r küme bazında aralarında asal polinomlarıdır. Daha doğrusu, örtük denklem xr(t) - p(t) ve yr(t) - q(t)'nin t'ye göre .
Daha yüksek boyutlarda (ikiden fazla koordinat veya birden fazla parametre), rasyonel parametrik denklemlerin örtükleştirilmesi hesaplamasıyla yapılabilir; bkz .
Yarıçapı a olan çember örneğini ele alırsak, parametrik denklemler;

x ve y terimlerinde aracılığıyla örtükleştirilebilir.

değerlerini

özdeşliğinde yerine koyarak

elde ederiz ve buradan

bulunur. Bu da orijin merkezli bir çemberin standart denklemidir.
İki boyutta örnekler
Parabol
Bir parabol için en basit denklem olan,

serbest bir parametre t kullanılarak (basit bir şekilde) parametrelendirilebilir ve

elde edilir.
Açık denklemler
Daha genel olarak, açık bir denklemle verilen herhangi bir eğri,
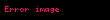
serbest bir parametre t kullanılarak (basit bir şekilde) parametrelendirilebilir ve

bulunur.
Çember
Daha kapsamlı bir örnek ise aşağıdaki gibidir. Sıradan (Kartezyen) denklemle tanımlanan birim çemberi düşünün;

Bu denklem aşağıdaki gibi parametrelendirilebilir:
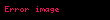
Kartezyen denklem ile bir noktanın çember üzerinde olup olmadığını kontrol etmek daha kolaydır. Parametrik seçenek ile bir çizim üzerinde noktalar elde etmek daha kolaydır.
Bazı bağlamlarda, eğer varsa, sadece (yani iki polinomun kesirlerini) içeren parametrik denklemler tercih edilir. Çember durumunda, böyle bir rasyonel parametrelendirme şöyledir:

Bu parametrik denklem çifti ile (-1, 0) noktası t'nin gerçek değeri ile değil, t sonsuza yöneldiğinde x ve y'nin limit değeri ile temsil edilir.
Elips
Yarı eksenleri a ve b olan kanonik konumdaki bir elips (merkezi orijinde, ana eksen x ekseni boyunca) parametrik olarak şu şekilde gösterilebilir:

Genel konumdaki bir elips şu şekilde ifade edilebilir:

t parametresi 0 ile 2π arasında değişir. Burada (Xc , Yc) elipsin merkezidir ve φ x ekseni ile elipsin ana ekseni arasındaki açıdır.
Her iki parametrelendirme de kullanılarak ve

alınarak yapılabilir.
Lissajous eğrisi

Bir Lissajous eğrisi elipse benzer, ancak x ve y fazda değildir. Kanonik konumda, bir Lissajous eğrisi şu şekilde verilir:
burada kx ve ky şeklin lob sayısını tanımlayan sabitlerdir.
Hiperbol
Doğu-batı açılımlı bir hiperbol parametrik olarak şu şekilde gösterilebilir:
veya, olarak,

Kuzey-güney açılımlı bir hiperbol parametrik olarak şu şekilde gösterilebilir:

veya, rasyonel olarak

Tüm bu formüllerde (h , k) hiperbolün merkez koordinatları, a yarı büyük eksenin uzunluğu ve b yarı küçük eksenin uzunluğudur. Bu formüllerin rasyonel formlarında, sırasıyla (-a , 0) ve (0 , -a) noktalarının t'nin gerçek bir değeriyle temsil edilmediğine, t sonsuza giderken x ve y'nin limiti olduğuna dikkat edin.
Hipotrokoid
Bir hipotrokoid, r yarıçaplı bir çembere bağlı bir noktanın, R yarıçaplı sabit bir çemberin içinde yuvarlanmasıyla izlenen bir eğridir; burada nokta, iç çemberin merkezinden d uzaklıktadır.
-
![image]() r = d olan bir hipotrokoid
r = d olan bir hipotrokoid -
![image]() R = 5, r = 3, d = 5 olan bir hipotrokoid
R = 5, r = 3, d = 5 olan bir hipotrokoid
Hipotrokoidler için parametrik denklemler şunlardır:

Bazı örnekler:
-
![image]() R = 6 r = 4 d = 1
R = 6 r = 4 d = 1 -
![image]() R = 7 r = 4 d = 1
R = 7 r = 4 d = 1 -
![image]() R = 8 r = 3 d = 2
R = 8 r = 3 d = 2 -
![image]() R = 7 r = 4 d = 2
R = 7 r = 4 d = 2 -
![image]() R = 15 r = 14 d = 1
R = 15 r = 14 d = 1
Üç boyutta örnekler
Helezon

Parametrik denklemler yüksek boyutlu uzaylarda eğrileri tanımlamak için uygundur. Örneğin:

yarıçapı a olan ve dönüş başına 2πb birim yükselen üç boyutlu bir eğriyi, helezon tanımlar. Denklemler düzlemde bir çember için olanlarla aynıdır.
Yukarıdaki gibi ifadeler genellikle şu şekilde yazılır:

burada r üç boyutlu bir vektördür.
Parametrik yüzeyler
Büyük yarıçapı R ve küçük yarıçapı r olan bir torus, parametrik olarak şu şekilde tanımlanabilir:

burada t ve u parametrelerinin her ikisi de 0 ile 2π arasında değişir.
-
![image]() R = 2, r = 1/2
R = 2, r = 1/2
u, 0 ile 2π arasında değişirken, yüzeydeki nokta torustaki delikten geçen kısa bir çember etrafında hareket eder. t, 0 ile 2π arasında değiştikçe yüzeydeki nokta torustaki deliğin etrafında uzun bir çember çizer.
Vektörlerle örnek



şeklindedir.
Eksik belirlenmiş doğrusal sistemler
n bilinmeyenli bir m doğrusal denklem sistemi birden fazla çözüme sahipse . Bu durum, sistemin matris ve aynı rank r'ye sahip ve r < m olduğunda ortaya çıkar. Bu durumda, m - r bilinmeyenleri parametre olarak seçilebilir ve tüm çözümleri, tüm bilinmeyenlerin seçilenlerin doğrusal birleşimi olarak ifade edildiği parametrik bir denklem olarak temsil eder.
Yani, bilinmeyenler 

Böyle bir parametrik denklem, sistemin çözümünün parametrik formu olarak adlandırılır.
Çözümün parametrik formunu hesaplamak için standart yöntem, artırılmış matrisin (indirgenmiş satır eşelon formunu) hesaplamak için Gauss eliminasyonu kullanmaktır. Daha sonra parametre olarak kullanılabilecek bilinmeyenler, herhangi bir (başat girdi) içermeyen sütunlara karşılık gelenlerdir (yani bir satırdaki veya matristeki en soldaki sıfır olmayan giriş) ve parametrik form doğrudan çıkarılabilir.
Ayrıca bakınız
Kaynakça
- ^ a b c Eric W. Weisstein, Parametric Equations (MathWorld)
- ^ (1972). Advanced Engineering Mathematics. 3rd. New York: . ss. 291,342. ISBN .
- ^ Burden, Richard L.; Faires, J. Douglas (1993). Numerical Analysis. 5th. Boston: Brookes/Cole. s. 149. ISBN .
- ^ Thomas, George B.; Finney, Ross L. (1979). Calculus and Analytic Geometry. fifth. Addison-Wesley. s. 91.
- ^ Nykamp, Duane. . mathinsight.org. 12 Ekim 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 14 Nisan 2017.
- ^ Spitzbart, Abraham (1975). Calculus with Analytic Geometry
![image]() . Gleview, IL: Scott, Foresman and Company. ISBN . Erişim tarihi: 30 Ağustos 2015.
. Gleview, IL: Scott, Foresman and Company. ISBN . Erişim tarihi: 30 Ağustos 2015. - ^ Stewart, James (2003). Calculus. 5th. Belmont, CA: Thomson Learning, Inc. ss. 687-689. ISBN .
- ^ Shah, Jami J.; Martti Mantyla (1995). Parametric and feature-based CAD/CAM: concepts, techniques, and applications. New York, NY: John Wiley & Sons, Inc. ss. 29-31. ISBN .
- ^ Calculus: Single and Multivariable. John Wiley. 29 Ekim 2012. s. 919. ISBN . OCLC 828768012.
- ^ a b c Anton, Howard; Rorres, Chris (2014) [1973]. "1.2 Gaussian Elimination". Elementary Linear Algebra. 11th. Wiley. ss. 11-24.
Dış bağlantılar
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte bir parametrik denklem bir grup niceligi parametreler olarak adlandirilan bir veya daha fazla bagimsiz degiskenin fonksiyonlari olarak tanimlar Parametrik denklemler genellikle bir egri veya gibi geometrik bir nesneyi olusturan noktalarin koordinatlarini ifade etmek icin kullanilir ve sirasiyla parametrik egri ve parametrik yuzey olarak adlandirilir Bu gibi durumlarda denklemler toplu olarak nesnenin parametrik temsili veya parametrik sistem veya parametrelendirilmesi alternatif olarak parametrelendirme olarak yazilir olarak adlandirilir x ve y parametrik denklemleri ile tanimlanabilir Ornegin x cos ty sin t displaystyle begin aligned x amp cos t y amp sin t end aligned denklemleri t parametre olmak uzere birim cemberin parametrik bir temsilini olusturur Bir nokta x y birim cember uzerindedir ancak ve ancak t degeri varsa bu iki denklem o noktayi olusturur Bazen skaler cikti degiskenleri icin parametrik denklemler vektorler icinde tek bir parametrik denklemde birlestirilir x y cos t sin t displaystyle x y cos t sin t Parametrik gosterimler genellikle benzersiz degildir asagidaki Iki boyutta ornekler bolumune bakin bu nedenle ayni buyuklukler bir dizi farkli parametrelendirme ile ifade edilebilir Egriler ve yuzeylere ek olarak parametrik denklemler parametre sayisi manifoldun veya varyetenin boyutuna esit olacak sekilde daha yuksek boyutu olan manifoldlari ve cebirsel varyeteleri tanimlayabilir ve denklem sayisi manifold veya varyetenin goz onunde bulunduruldugu uzayin boyutuna esittir egriler icin boyut bir ve bir parametre kullanilir yuzeyler icin boyut iki ve iki parametre vb Parametrik denklemler genellikle kinematik alaninda kullanilir burada bir nesnenin yorungesi parametre olarak zamana bagli denklemlerle temsil edilir Bu uygulama nedeniyle tek bir parametre genellikle t olarak etiketlenir ancak parametreler diger fiziksel buyuklukleri geometrik degiskenler gibi temsil edebilir veya kolaylik saglamak icin keyfi olarak secilebilir Parametrelendirmeler benzersiz ve tek degildir birden fazla parametrik denklem kumesi ayni egriyi belirtebilir UygulamalariKinematik Kinematikte nesnelerin uzaydaki yollari genellikle parametrik egriler olarak tanimlanir ve her bir uzaysal koordinat acikca bagimsiz bir parametreye genellikle zaman baglidir Bu sekilde kullanildiginda nesnenin koordinatlari icin parametrik denklemler kumesi toplu olarak konum icin bir vektor degerli fonksiyon olusturur Bu tur parametrik egriler daha sonra terimsel olarak integrallenebilir ve turevlenebilir olabilir Boylece bir parcacigin konumu parametrik olarak soyle tanimlanirsar t x t y t z t displaystyle mathbf r t x t y t z t o zaman hiz su sekilde v t r t x t y t z t displaystyle begin aligned mathbf v t amp mathbf r t amp x t y t z t end aligned ve ivme de asagidaki gibi bulunabilira t v t r t x t y t z t displaystyle begin aligned mathbf a t amp mathbf v t mathbf r t amp x t y t z t end aligned Bilgisayar destekli tasarim Parametrik denklemlerin bir diger onemli kullanimi bilgisayar destekli tasarim CAD alanindadir Ornegin hepsi duzlemsel egrileri tanimlamak icin yaygin olarak kullanilan asagidaki uc gosterimi inceleyin Tur Bicim Ornek TanimAcik y f x displaystyle y f x y mx b displaystyle y mx b DogruOrtuk f x y 0 displaystyle f x y 0 x a 2 y b 2 r2 displaystyle left x a right 2 left y b right 2 r 2 CemberParametrik x g t w t displaystyle x frac g t w t y h t w t displaystyle y frac h t w t x a0 a1t displaystyle x a 0 a 1 t y b0 b1t displaystyle y b 0 b 1 t Dogrux a rcos t displaystyle x a r cos t y b rsin t displaystyle y b r sin t Cember Her bir gosterimin CAD uygulamalari icin avantajlari ve dezavantajlari vardir Acik gosterim cok karmasik olabilir hatta mevcut olmayabilir Dahasi ve ozellikle de altinda iyi sonuc vermez Ote yandan parametrik bir denklem ve ortuk bir denklem acik bir gosterimden kolayca cikarilabileceginden basit bir acik gosterim mevcut oldugunda diger iki gosterimin avantajlarina sahiptir Ortuk gosterimler egri uzerinde noktalar olusturmayi ve hatta gercek noktalar olup olmadigina karar vermeyi zorlastirabilir Ote yandan verilen bir noktanin bir egri uzerinde olup olmadigina veya kapali bir egrinin icinde mi yoksa disinda mi olduguna karar vermek icin cok uygundurlar Bu tur kararlar parametrik bir gosterimle zor olabilir ancak parametrik gosterimler bir egri uzerinde noktalar olusturmak ve bunu cizmek icin en uygun olanidir Tam sayi geometrisi alanindaki cok sayida problem parametrik denklemler kullanilarak cozulebilir Bu tur klasik bir cozum Oklid in dik ucgenleri kenarlarinin a b ve hipotenuslerinin c uzunluklari aralarinda asal tam sayilar olacak sekilde parametrize etmesidir a ve b cift olmadigindan aksi takdirde a b ve c cift olmazdi a cift olacak sekilde degistirilebilir ve parametrelendirme su sekilde olur a 2mnb m2 n2c m2 n2 displaystyle begin aligned a amp 2mn b amp m 2 n 2 c amp m 2 n 2 end aligned burada m ve n parametreleri her ikisi de tek olmayan pozitif aralarinda asal tam sayilardir a b ve c yi rastgele bir pozitif tam sayi ile carparak uc kenari tam sayi uzunlugunda olan tum dik ucgenlerin parametrizasyonunu elde ederiz OrtuklestirmeBir dizi parametrik denklemin tek bir donusturulmesi t degiskeninin eszamanli x f t y g t displaystyle x f t y g t denklemlerinden cikarilmasini icerir Bu islem ortuklestirme Ingilizce implicitization olarak adlandirilir Bu denklemlerden biri t icin cozulebilirse elde edilen ifade diger denklemde yerine konularak yalnizca x ve y iceren bir denklem elde edilebilir y g t displaystyle y g t cozulerek t g 1 y displaystyle t g 1 y elde edilir ve bu x f t displaystyle x f t icinde kullanilirsa x f g 1 y displaystyle x f g 1 y acik denklemini verirken daha karmasik durumlarda h x y 0 displaystyle h x y 0 seklinde ortuk bir denklem elde edilir Eger parametrizasyon x p t r t y q t r t displaystyle x frac p t r t qquad y frac q t r t tarafindan veriliyorsa bir hesaplamasi ortuklestirmeye izin verir burada p q ve r kume bazinda aralarinda asal polinomlaridir Daha dogrusu ortuk denklem xr t p t ve yr t q t nin t ye gore Daha yuksek boyutlarda ikiden fazla koordinat veya birden fazla parametre rasyonel parametrik denklemlerin ortuklestirilmesi hesaplamasiyla yapilabilir bkz Yaricapi a olan cember ornegini ele alirsak parametrik denklemler x acos t y asin t displaystyle begin aligned x amp a cos t y amp a sin t end aligned x ve y terimlerinde araciligiyla ortuklestirilebilir xa cos t ya sin t displaystyle begin aligned frac x a amp cos t frac y a amp sin t end aligned degerlerinicos t 2 sin t 2 1 displaystyle cos t 2 sin t 2 1 ozdesliginde yerine koyarak xa 2 ya 2 1 displaystyle left frac x a right 2 left frac y a right 2 1 elde ederiz ve buradanx2 y2 a2 displaystyle x 2 y 2 a 2 bulunur Bu da orijin merkezli bir cemberin standart denklemidir Iki boyutta orneklerParabol Bir parabol icin en basit denklem olan y x2 displaystyle y x 2 serbest bir parametre t kullanilarak basit bir sekilde parametrelendirilebilir vex t y t2for lt t lt displaystyle x t y t 2 quad mathrm for infty lt t lt infty elde edilir Acik denklemler Daha genel olarak acik bir denklemle verilen herhangi bir egri y f x displaystyle y f x serbest bir parametre t kullanilarak basit bir sekilde parametrelendirilebilir vex t y f t for lt t lt displaystyle x t y f t quad mathrm for infty lt t lt infty bulunur Cember Daha kapsamli bir ornek ise asagidaki gibidir Siradan Kartezyen denklemle tanimlanan birim cemberi dusunun x2 y2 1 displaystyle x 2 y 2 1 Bu denklem asagidaki gibi parametrelendirilebilir x y cos t sin t for 0 t lt 2p displaystyle x y cos t sin t quad mathrm for 0 leq t lt 2 pi Kartezyen denklem ile bir noktanin cember uzerinde olup olmadigini kontrol etmek daha kolaydir Parametrik secenek ile bir cizim uzerinde noktalar elde etmek daha kolaydir Bazi baglamlarda eger varsa sadece yani iki polinomun kesirlerini iceren parametrik denklemler tercih edilir Cember durumunda boyle bir rasyonel parametrelendirme soyledir x 1 t21 t2y 2t1 t2 displaystyle begin aligned x amp frac 1 t 2 1 t 2 y amp frac 2t 1 t 2 end aligned Bu parametrik denklem cifti ile 1 0 noktasi t nin gercek degeri ile degil t sonsuza yoneldiginde x ve y nin limit degeri ile temsil edilir Elips Yari eksenleri a ve b olan kanonik konumdaki bir elips merkezi orijinde ana eksen x ekseni boyunca parametrik olarak su sekilde gosterilebilir x acos ty bsin t displaystyle begin aligned x amp a cos t y amp b sin t end aligned Genel konumdaki bir elips su sekilde ifade edilebilir x Xc acos tcos f bsin tsin fy Yc acos tsin f bsin tcos f displaystyle begin alignedat 4 x amp amp X mathrm c amp a cos t cos varphi amp amp b sin t sin varphi y amp amp Y mathrm c amp a cos t sin varphi amp amp b sin t cos varphi end alignedat t parametresi 0 ile 2p arasinda degisir Burada Xc Yc elipsin merkezidir ve f x ekseni ile elipsin ana ekseni arasindaki acidir Her iki parametrelendirme de kullanilarak ve tan t2 u textstyle tan frac t 2 u alinarak yapilabilir Lissajous egrisi Lissajous egrisi kx 3 ve ky 2 Bir Lissajous egrisi elipse benzer ancak x ve y fazda degildir Kanonik konumda bir Lissajous egrisi su sekilde verilir x acos kxt y bsin kyt displaystyle begin aligned x amp a cos k x t y amp b sin k y t end aligned burada kx ve ky seklin lob sayisini tanimlayan sabitlerdir Hiperbol Dogu bati acilimli bir hiperbol parametrik olarak su sekilde gosterilebilir x asec t hy btan t k displaystyle begin aligned x amp a sec t h y amp b tan t k end aligned veya olarak x a1 t21 t2 hy b2t1 t2 k displaystyle begin aligned x amp a frac 1 t 2 1 t 2 h y amp b frac 2t 1 t 2 k end aligned Kuzey guney acilimli bir hiperbol parametrik olarak su sekilde gosterilebilir x btan t hy asec t k displaystyle begin aligned x amp b tan t h y amp a sec t k end aligned veya rasyonel olarakx b2t1 t2 hy a1 t21 t2 k displaystyle begin aligned x amp b frac 2t 1 t 2 h y amp a frac 1 t 2 1 t 2 k end aligned Tum bu formullerde h k hiperbolun merkez koordinatlari a yari buyuk eksenin uzunlugu ve b yari kucuk eksenin uzunlugudur Bu formullerin rasyonel formlarinda sirasiyla a 0 ve 0 a noktalarinin t nin gercek bir degeriyle temsil edilmedigine t sonsuza giderken x ve y nin limiti olduguna dikkat edin Hipotrokoid Bir hipotrokoid r yaricapli bir cembere bagli bir noktanin R yaricapli sabit bir cemberin icinde yuvarlanmasiyla izlenen bir egridir burada nokta ic cemberin merkezinden d uzakliktadir r d olan bir hipotrokoid R 5 r 3 d 5 olan bir hipotrokoid Hipotrokoidler icin parametrik denklemler sunlardir x 8 R r cos 8 dcos R rr8 y 8 R r sin 8 dsin R rr8 displaystyle begin aligned x theta amp R r cos theta d cos left R r over r theta right y theta amp R r sin theta d sin left R r over r theta right end aligned Bazi ornekler R 6 r 4 d 1 R 7 r 4 d 1 R 8 r 3 d 2 R 7 r 4 d 2 R 15 r 14 d 1Uc boyutta ornekler source source source source source source source source source Animasyonlu parametrik helezonHelezon Parametrik helezon Parametrik denklemler yuksek boyutlu uzaylarda egrileri tanimlamak icin uygundur Ornegin x acos t y asin t z bt displaystyle begin aligned x amp a cos t y amp a sin t z amp bt end aligned yaricapi a olan ve donus basina 2p b birim yukselen uc boyutlu bir egriyi helezon tanimlar Denklemler duzlemde bir cember icin olanlarla aynidir Yukaridaki gibi ifadeler genellikle su sekilde yazilir r t x t y t z t acos t asin t bt displaystyle begin aligned mathbf r t amp x t y t z t amp a cos t a sin t bt end aligned burada r uc boyutlu bir vektordur Parametrik yuzeyler Buyuk yaricapi R ve kucuk yaricapi r olan bir torus parametrik olarak su sekilde tanimlanabilir x cos t R rcos u y sin t R rcos u z rsin u displaystyle begin aligned x amp cos t left R r cos u right y amp sin t left R r cos u right z amp r sin u end aligned burada t ve u parametrelerinin her ikisi de 0 ile 2p arasinda degisir R 2 r 1 2 u 0 ile 2p arasinda degisirken yuzeydeki nokta torustaki delikten gecen kisa bir cember etrafinda hareket eder t 0 ile 2p arasinda degistikce yuzeydeki nokta torustaki deligin etrafinda uzun bir cember cizer Vektorlerle ornek x0 y0 z0 displaystyle left x 0 y 0 z 0 right noktasindan gecen ve ai bj ck displaystyle a hat mathbf i b hat mathbf j c hat mathbf k vektorune paralel olan dogrunun parametrik denklemi x x0 aty y0 btz z0 ct displaystyle begin aligned x amp x 0 at y amp y 0 bt z amp z 0 ct end aligned seklindedir Eksik belirlenmis dogrusal sistemlern bilinmeyenli bir m dogrusal denklem sistemi birden fazla cozume sahipse Bu durum sistemin matris ve ayni rank r ye sahip ve r lt m oldugunda ortaya cikar Bu durumda m r bilinmeyenleri parametre olarak secilebilir ve tum cozumleri tum bilinmeyenlerin secilenlerin dogrusal birlesimi olarak ifade edildigi parametrik bir denklem olarak temsil eder Yani bilinmeyenler x1 xn displaystyle x 1 ldots x n ise cozumleri su sekilde ifade etmek icin bunlari yeniden duzenleyebiliriz x1 b1 j r 1na1 jxj xr br j r 1nar jxjxr 1 xr 1 xn xn displaystyle begin aligned x 1 amp beta 1 sum j r 1 n alpha 1 j x j vdots x r amp beta r sum j r 1 n alpha r j x j x r 1 amp x r 1 vdots x n amp x n end aligned Boyle bir parametrik denklem sistemin cozumunun parametrik formu olarak adlandirilir Cozumun parametrik formunu hesaplamak icin standart yontem artirilmis matrisin indirgenmis satir eselon formunu hesaplamak icin Gauss eliminasyonu kullanmaktir Daha sonra parametre olarak kullanilabilecek bilinmeyenler herhangi bir basat girdi icermeyen sutunlara karsilik gelenlerdir yani bir satirdaki veya matristeki en soldaki sifir olmayan giris ve parametrik form dogrudan cikarilabilir Ayrica bakinizEgri Vektor degerli fonksiyonKaynakca a b c Eric W Weisstein Parametric Equations MathWorld 1972 Advanced Engineering Mathematics 3rd New York Wiley ss 291 342 ISBN 0 471 50728 8 Burden Richard L Faires J Douglas 1993 Numerical Analysis 5th Boston Brookes Cole s 149 ISBN 0 534 93219 3 Thomas George B Finney Ross L 1979 Calculus and Analytic Geometry fifth Addison Wesley s 91 Nykamp Duane mathinsight org 12 Ekim 2011 tarihinde kaynagindan arsivlendi Erisim tarihi 14 Nisan 2017 Spitzbart Abraham 1975 Calculus with Analytic Geometry Gleview IL Scott Foresman and Company ISBN 0 673 07907 4 Erisim tarihi 30 Agustos 2015 Stewart James 2003 Calculus 5th Belmont CA Thomson Learning Inc ss 687 689 ISBN 0 534 39339 X Shah Jami J Martti Mantyla 1995 Parametric and feature based CAD CAM concepts techniques and applications New York NY John Wiley amp Sons Inc ss 29 31 ISBN 0 471 00214 3 Calculus Single and Multivariable John Wiley 29 Ekim 2012 s 919 ISBN 9780470888612 OCLC 828768012 a b c Anton Howard Rorres Chris 2014 1973 1 2 Gaussian Elimination Elementary Linear Algebra 11th Wiley ss 11 24 Dis baglantilarCurlie de Graphing Software DMOZ tabanli Web application to draw parametric curves on the plane
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State