Dış açı teoremi, bir üçgenin bir dış açısının ölçüsünün, uzak iç açılarının ölçülerinden daha büyük olduğunu belirten Ökllid'in Elemanlar'ı Önerme 1.16'dır. Bu, mutlak geometride temel bir sonuçtur çünkü ispatı bağlı değildir.
Birkaç lise geometri incelemesinde, "dış açı teoremi" terimi farklı bir sonuca, yani Önerme 1.32'nin bir üçgenin dış açısının ölçüsünün uzak iç açıların ölçüleri toplamına eşit olduğunu belirten bölüme uygulanmıştır. Öklid'in bağlı olan bu sonuç, onu Öklid dış açı teoreminden ayırmak için "Lise dış açı teoremi" (LDAT-HSEAT: High school exterior angle theorem) olarak anılacaktır.
Bazı yazarlar, dış açı teoreminin güçlü biçimi olarak "Lise dış açı teoremi" ve zayıf biçimi olarak "Öklid dış açı teoremi" olarak adlandırırlar.
Dış açılar
Bir üçgenin tepe noktası (verteks) adı verilen üç köşesi bulunur. Bir tepe noktasında bir araya gelen üçgenin iki kenarı (çizgi parçaları) iki açı oluşturur (üçgenin kenarlarının çizgi parçaları yerine doğrular olduğunu düşünürsek dört açı oluşturur). Bu açılardan sadece bir tanesi iç kısmında üçgenin üçüncü kenarı tarafında kalır ve bu açıya üçgenin iç açısı denir. Aşağıdaki resimde 

Öklid dış açı teoremi
Öklid tarafından verilen Önerme 1.16'nın ispatı, genellikle Öklid'in kusurlu bir kanıt sunduğu bir yer olarak gösterilmektedir.
Öklid, dış açı teoremini şu şekilde kanıtlar:
doğru parçasının
orta noktasını bulun,
ışınını çizin,
noktasını
ışını üzerinde çizin, böylece
(aynı zamanda)
ve
'nin orta noktası olur,
doğru parçasını çizin.
Eş üçgenler vasıtasıyla, 

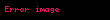
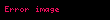
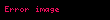
Kusur, bir noktanın (yukarıda, 
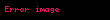
Küresel geometride geçersiz

Dış açı teoremi, küresel geometride veya ilgili eliptik geometride geçerli değildir. Biri Kuzey Kutbu olan ve diğer ikisi ekvator üzerinde bulunan küresel bir üçgen düşünün. Kuzey Kutbu'ndan çıkan üçgenin kenarları (kürenin büyük çemberleri) her ikisi de ekvatoru dik açılarda karşılamaktadır, bu nedenle bu üçgenin uzak bir iç açıya eşit bir dış açısı vardır. Diğer iç açı (Kuzey Kutbu'nda) 90°'den daha büyük yapılabilir, bu da bu ifadenin kusurunu vurgulamaktadır. Bununla birlikte, Öklid'in dış açı teoremi mutlak geometride bir teorem olduğundan, hiperbolik geometride otomatik olarak geçerlidir.
Lise dış açı teoremi
Lise dış açı teoremi (LDAT), bir üçgenin tepe noktasındaki dış açının boyutunun, üçgenin diğer iki köşesindeki iç açıların boyutlarının toplamına eşit olduğunu söyler (uzak iç açılar). Bu nedenle, resimde 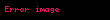
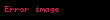
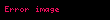
LDAT mantıksal olarak bir üçgenin açılarının toplamının 180° olduğu şeklindeki Öklid ifadesine eşdeğerdir. Bir üçgende açıların ölçülerinin toplamının 180° olduğu biliniyorsa, LDAT aşağıdaki şekilde ispatlanır:
Öte yandan, LDAT doğru bir ifade olarak alınırsa:

Bir üçgenin açılarının ölçülerinin toplamının 180° olduğunu kanıtlamak.
LDAT'nin Öklid kanıtı (ve aynı anda bir üçgenin açılarının toplamı üzerindeki sonuç) 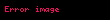

LDAT, bir üçgende bilinmeyen açıların ölçülerini hesaplamaya çalışırken son derece yararlı olabilir.
Notlar
- ^ Henderson & Taimiņa 2005, s. 110
- ^ Wylie, Jr. 1964, s. 101 & s. 106
- ^ Bir doğru parçasının iki ucundan biri başlangıç tarafı ve diğeri de son taraf olarak kabul edilir. Açı, başlangıç tarafından son tarafa saat yönünün tersine gidilerek oluşturulur. Doğru parçasının hangi kenarının başlangıç olduğunun seçimi isteğe bağlıdır, bu nedenle doğru parçaları tarafından oluşturulan açı için iki olasılık vardır.
- ^ İç açıları bu şekilde tanımlamak bir üçgenin açılarının toplamının 180 derece olduğunu varsaymaz.
- ^ Faber 1983, s. 113
- ^ a b Greenberg 1974, s. 99
- ^ Venema 2006, s. 10
- ^ Heath 1956, Vol. 1, s. 316
Kaynakça
- Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, Inc., ISBN
- (1974), Euclidean and Non-Euclidean Geometries/Development and History, San Francisco: W.H. Freeman, ISBN
- Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] bas.). New York: Dover Publications.
- (3 vols.): (vol. 1), (vol. 2), (vol. 3).
- Henderson, David W.; Taimiņa, Daina (2005), Experiencing Geometry/Euclidean and Non-Euclidean with History, 3rd, Pearson/Prentice-Hall, ISBN
- Venema, Gerard A. (2006), Foundations of Geometry, Upper Saddle River, NJ: Pearson Prentice Hall, ISBN
- Wylie Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill
LDAT kaynakları
- Geometry Textbook - Standard IX, Maharashtra State Board of Secondary and Higher Secondary Education, Pune - 411 005, India.
- Geometry Common Core, 'Pearson Education: Upper Saddle River, ©2010, pages 171-173 | Amerika Birleşik Devletleri.
- Wheater, Carolyn C. (2007). Homework Helpers: Geometry. Franklin Lakes, NJ: Career Press. ss. 88-90. ISBN ..
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Dis aci teoremi bir ucgenin bir dis acisinin olcusunun uzak ic acilarinin olculerinden daha buyuk oldugunu belirten Okllid in Elemanlar i Onerme 1 16 dir Bu mutlak geometride temel bir sonuctur cunku ispati bagli degildir Birkac lise geometri incelemesinde dis aci teoremi terimi farkli bir sonuca yani Onerme 1 32 nin bir ucgenin dis acisinin olcusunun uzak ic acilarin olculeri toplamina esit oldugunu belirten bolume uygulanmistir Oklid in bagli olan bu sonuc onu Oklid dis aci teoreminden ayirmak icin Lise dis aci teoremi LDAT HSEAT High school exterior angle theorem olarak anilacaktir Bazi yazarlar dis aci teoreminin guclu bicimi olarak Lise dis aci teoremi ve zayif bicimi olarak Oklid dis aci teoremi olarak adlandirirlar Dis acilarBir ucgenin tepe noktasi verteks adi verilen uc kosesi bulunur Bir tepe noktasinda bir araya gelen ucgenin iki kenari cizgi parcalari iki aci olusturur ucgenin kenarlarinin cizgi parcalari yerine dogrular oldugunu dusunursek dort aci olusturur Bu acilardan sadece bir tanesi ic kisminda ucgenin ucuncu kenari tarafinda kalir ve bu aciya ucgenin ic acisi denir Asagidaki resimde ABC textstyle angle ABC BCA textstyle angle BCA ve CAB textstyle angle CAB acilari ucgenin uc ic acisidir Ucgenin kenarlarindan birinin uzatilmasiyla bir dis aci olusturulur uzatilmis taraf ile diger taraf arasindaki aci dis acidir Resimde ACD textstyle angle ACD acisi bir dis acidir Oklid dis aci teoremiOklid tarafindan verilen Onerme 1 16 nin ispati genellikle Oklid in kusurlu bir kanit sundugu bir yer olarak gosterilmektedir Oklid dis aci teoremini su sekilde kanitlar AC textstyle AC dogru parcasinin E textstyle E orta noktasini bulun BE textstyle BE isinini cizin F textstyle F noktasini BE textstyle BE isini uzerinde cizin boylece E textstyle E ayni zamanda B textstyle B ve F textstyle F nin orta noktasi olur FC textstyle FC dogru parcasini cizin Es ucgenler vasitasiyla BAC textstyle angle BAC ECF textstyle angle ECF ve ECF textstyle angle ECF nin ECD textstyle angle ECD den daha kucuk oldugu ECD textstyle angle ECD ACD textstyle angle ACD oldugu sonucuna varabiliriz bu nedenle BAC textstyle angle BAC acisi ACD textstyle angle ACD den kucuktur ve ayni sey CBA textstyle angle CBA acisi icin BC textstyle BC yi ikiye bolerek yapilabilir Kusur bir noktanin yukarida F textstyle F ic aci ACD textstyle angle ACD oldugu varsayiminda yatmaktadir Bu iddia icin hicbir neden belirtilmemistir ancak devamindaki diyagram onu gercek bir ifade gibi gosterir Oklid geometrisi icin tam bir aksiyom seti kullanildiginda bkz bu Oklid savi kanitlanabilir Kuresel geometride gecersiz Kucuk ucgenler neredeyse Oklid tarzinda davranabilir ancak buyuk ucgenin tabanindaki dis acilar Oklid in dis aci teoremine bir celiski olarak 90 dir Dis aci teoremi kuresel geometride veya ilgili eliptik geometride gecerli degildir Biri Kuzey Kutbu olan ve diger ikisi ekvator uzerinde bulunan kuresel bir ucgen dusunun Kuzey Kutbu ndan cikan ucgenin kenarlari kurenin buyuk cemberleri her ikisi de ekvatoru dik acilarda karsilamaktadir bu nedenle bu ucgenin uzak bir ic aciya esit bir dis acisi vardir Diger ic aci Kuzey Kutbu nda 90 den daha buyuk yapilabilir bu da bu ifadenin kusurunu vurgulamaktadir Bununla birlikte Oklid in dis aci teoremi mutlak geometride bir teorem oldugundan hiperbolik geometride otomatik olarak gecerlidir Lise dis aci teoremiLise dis aci teoremi LDAT bir ucgenin tepe noktasindaki dis acinin boyutunun ucgenin diger iki kosesindeki ic acilarin boyutlarinin toplamina esit oldugunu soyler uzak ic acilar Bu nedenle resimde ACD textstyle angle ACD acisinin boyutu ABC textstyle angle ABC acisinin boyutu arti CAB textstyle angle CAB acisinin boyutuna esittir LDAT mantiksal olarak bir ucgenin acilarinin toplaminin 180 oldugu seklindeki Oklid ifadesine esdegerdir Bir ucgende acilarin olculerinin toplaminin 180 oldugu biliniyorsa LDAT asagidaki sekilde ispatlanir b d 180 displaystyle b d 180 circ b d b a c displaystyle b d b a c d a c displaystyle therefore d a c Ote yandan LDAT dogru bir ifade olarak alinirsa d a c displaystyle d a c b d 180 displaystyle b d 180 circ b a c 180 displaystyle therefore b a c 180 circ LDAT kanitinin cizimi Bir ucgenin acilarinin olculerinin toplaminin 180 oldugunu kanitlamak LDAT nin Oklid kaniti ve ayni anda bir ucgenin acilarinin toplami uzerindeki sonuc C textstyle C noktasindan gecen AB textstyle AB tarafina paralel bir cizgi olusturarak ve ardindan sonucu resimdeki gibi elde etmek uzere karsilik gelen acilarin ozelliklerini ve paralel cizgilerin alternatif ic acilarini kullanarak baslar LDAT bir ucgende bilinmeyen acilarin olculerini hesaplamaya calisirken son derece yararli olabilir Notlar Henderson amp Taimina 2005 s 110 Wylie Jr 1964 s 101 amp s 106 Bir dogru parcasinin iki ucundan biri baslangic tarafi ve digeri de son taraf olarak kabul edilir Aci baslangic tarafindan son tarafa saat yonunun tersine gidilerek olusturulur Dogru parcasinin hangi kenarinin baslangic oldugunun secimi istege baglidir bu nedenle dogru parcalari tarafindan olusturulan aci icin iki olasilik vardir Ic acilari bu sekilde tanimlamak bir ucgenin acilarinin toplaminin 180 derece oldugunu varsaymaz Faber 1983 s 113 a b Greenberg 1974 s 99 Venema 2006 s 10 Heath 1956 Vol 1 s 316KaynakcaFaber Richard L 1983 Foundations of Euclidean and Non Euclidean Geometry New York Marcel Dekker Inc ISBN 0 8247 1748 1 1974 Euclidean and Non Euclidean Geometries Development and History San Francisco W H Freeman ISBN 0 7167 0454 4 Heath Thomas L 1956 The Thirteen Books of Euclid s Elements 2nd ed Facsimile Original publication Cambridge University Press 1925 bas New York Dover Publications 3 vols 0 486 60088 2 vol 1 0 486 60089 0 vol 2 0 486 60090 4 vol 3 Henderson David W Taimina Daina 2005 Experiencing Geometry Euclidean and Non Euclidean with History 3rd Pearson Prentice Hall ISBN 0 13 143748 8 Venema Gerard A 2006 Foundations of Geometry Upper Saddle River NJ Pearson Prentice Hall ISBN 0 13 143700 3 Wylie Jr C R 1964 Foundations of Geometry New York McGraw Hill LDAT kaynaklari Geometry Textbook Standard IX Maharashtra State Board of Secondary and Higher Secondary Education Pune 411 005 India Geometry Common Core Pearson Education Upper Saddle River c 2010 pages 171 173 Amerika Birlesik Devletleri Wheater Carolyn C 2007 Homework Helpers Geometry Franklin Lakes NJ Career Press ss 88 90 ISBN 978 1 56414 936 7
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State