Eski Mısır matematiği

Eski Mısır matematiği, Eski Mısır'da yaklaşık MÖ 3000 ila 300 yılları arasında, Eski Mısır Krallığı'ndan kabaca Helenistik Mısır'ın başlangıcına kadar geliştirilen ve kullanılan matematiktir. Eski Mısırlılar, saymak ve genellikle çarpma ve kesirleri içeren yazılı matematik problemlerini çözmek için bir sayı sistemi kullandılar. Mısır matematiğinin kanıtı, papirüs üzerine yazılmış, hayatta kalan az sayıda kaynakla sınırlıdır. Bu metinlerden, eski Mısırlıların, mimari mühendislik için yararlı olan üç boyutlu şekillerin yüzey alanını ve hacmini belirlemek gibi geometri kavramlarını ve sabit kesen yöntemi (Latince: regula falsi, İngilizce: false position method) ve ikinci dereceden denklemler gibi cebir kavramlarını anladıkları bilinmektedir.

Genel Bakış

Abydos'taki Tomb U-j'de bulunan fildişi etiketlerle matematiğin kullanımının yazılı kanıtı en az MÖ 3200'e kadar uzanmaktadır. Görünüşe göre bu etiketler mezar eşyaları için etiket olarak kullanılmış ve bazılarına rakamlar yazılmıştır. 400.000 öküz, 1.422.000 keçi ve 120.000 mahkûmun sunulmasını gösteren Narmer Macehead'de 10'lu taban sayı sisteminin kullanımına dair daha fazla kanıt bulunabilir.

Narmer Macehead (ön)

Narmer Macehead (arka)

Narmer Macehead'deki çizimler

Eski Krallık'ta (MÖ 2690-2180) matematiğin kullanımına ilişkin kanıtlar azdır, ancak Meidum'da bir mastaba yakınındaki duvardaki, mastabanın eğimi için yönergeler veren yazıtlardan bazı sonuçlar çıkarılabilir. Diyagramdaki çizgiler bir arşın aralıklarla dizilidir ve bu ölçü biriminin kullanımını göstermektedir.

En eski gerçek matematiksel belgeler, 12. Hanedanlığa (yaklaşık MÖ 1990–1800) aittir. Kahun Papirüsü'nün ve Berlin Papirüsü 6619 koleksiyonunun çok daha geniş bir parçası olan Moskova Papirüsü, , bu döneme tarihlenmektedir. İkinci Ara Dönem'e (MÖ 1650) tarihlenen Rhind Papirüsünün, 12. hanedandan daha eski bir matematiksel metne dayandığı söylenir.

Moskova Matematik Papirüsü ve Rhind Papirüsü, matematiksel problem metinleri olarak adlandırılır. Çözümleri olan bir dizi problemden oluşurlar. Bu metinler bir öğretmen veya tipik matematik problemlerini çözmekle uğraşan bir öğrenci tarafından yazılmış olabilir.

Eski Mısır matematiğinin ilginç bir özelliği, birim kesirlerin kullanılmasıdır. Mısırlılar, kesirler için 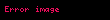${\displaystyle {\tfrac {1}{2}},{\tfrac {1}{3}}}$ ve ${\displaystyle {\tfrac {2}{3}}}$ gibi bazı özel gösterimler kullandılar ve bazı metinlerde ${\displaystyle {\tfrac {3}{4}}}$ için, ancak diğer kesirler tümü ${\displaystyle {\tfrac {1}{n}}}$ biçiminin birim kesirleri veya bu tür birim kesirlerin toplamları olarak yazılır. Yazıcılar, bu kesirlerle çalışmalarına yardımcı olmak için tablolar kullandılar. Örneğin Mısır Matematiksel Deri Rulosu, diğer birim kesirlerin toplamı olarak ifade edilen birim kesirler tablosudur. Rhind Papirüsü ve diğer bazı metinler ${\displaystyle {\tfrac {2}{n}}}$ tabloları içerir. Bu tablolar, yazarların ${\displaystyle {\tfrac {1}{n}}}$ biçiminin herhangi bir kısmını birim kesirlerin toplamı olarak yeniden yazmalarına olanak sağladı.

Yeni Krallık döneminde (yaklaşık MÖ 1550–1070) matematik problemlerinden edebi 'de bahsedilir ve Ramses III zamanından kalma 'da arazi ölçümleri kaydedilir. Deir el-Medina işçi köyünde, mezarların taş ocağında taşınırken rekor miktarda çamurun taşındığı birkaç ostraca (yazı yüzeyi olarak kullanılan bir çömlek parçası) bulundu.

Kaynakça

Eski Mısır matematiğini anlama çabaları günümüzde, mevcut kaynakların yetersizliği nedeniyle sekteye uğramaktadır. Var olan kaynaklar aşağıdaki metinleri içerir (bunlar genellikle Orta Krallık ve İkinci Ara Dönem'e tarihlenir):

• Moskova Papirüsü
• Mısır Matematiksel Deri Rulosu
• Lahun Matematiksel Papirüsü
• MÖ 1800 civarında yazılmış Berlin Papirüsü 6619
• Akhmim Ahşap Tableti
• Reisner Papirüsü, Mısır'ın erken 12. hanedanına tarihlenmektedir ve antik Thinis kasabası Nag el-Deir'de bulunmuştur.
• Rhind Papirüsü (RMP - Rhind Mathematical Papyrus), İkinci Ara Döneme (MÖ 1650) tarihlenir, ancak yazarı Ahmes, onu şimdi kaybolmuş bir Orta Krallık papirüsünün bir kopyası olarak tanımlar. RMP, en büyük matematiksel metindir.

Yeni Krallık'tan kalan, hesaplamalarla ilgili az miktarda matematiksel metin ve yazıt vardır:

• Papirüs Anastasi I, Hori adlı bir yazar tarafından yazılmış ve Amenemope adlı bir yazara hitaben (kurgusal) bir mektup olarak yazılmış bir edebi metindir. Mektubun bir bölümü birkaç matematik problemini tanımlar.
• Ostracon Senmut 153, hiyeratik olarak yazılmış bir metindir.
• Ostracon Turin 57170, hiyeratik olarak yazılmış bir metindir.
• Deir el-Medina'dan Ostraca, hesaplamalar içerir. Örneğin Ostracon IFAO 1206, muhtemelen bir mezarın taş ocakçılığı ile ilgili hacimlerin hesaplanmasını göstermektedir.

Sayılar

Mısırlılar eskiden sağdan sola yazarlardı ve sayının en önemsiz rakamları önce yazılırdı, böylece sonuçta sayıların sırası bizimkine karşılık gelirdi. Eski Mısır metinleri hiyeroglif veya hiyeratik olarak yazılabilir. Her iki gösterimde de sayı sistemi her zaman 10 tabanına göre verilmiştir. 1 sayısı basit bir vuruşla, 2 sayısı iki vuruşla vb. temsil edildi. 10, 100, 1.000, 10.000 ve 1.000.000 sayılarının kendi hiyeroglifleri vardı. 10 sayısı öküz çekmesi veya nal, 100 sayısı sarmal bir ip veya salyangoz ile temsil edilir, 1000 sayısı bir lotus çiçeği veya nilüfer çiçeği ile temsil edilir, 10.000 sayısı bir parmakla temsil edilir, 100.000 sayısı bir kurbağa veya iribaş ile ve bir milyon ise iki elini kaldırmış bir adam (Tanrı Heh olabilir) tarafından temsil edilir.

1 !! 10 !! 100 !! 1000 !! 10,000 !! 100,000 !! 1,000,000

Eski Mısır'da herhangi bir sayı iki şekilde yazılabilirdi: kelimelerle ve sayılarla. Örneğin, 30 sayısını yazmak için sıradan hiyeroglifler kullanılabilir:

veya aynısı sayılarla yazılırsa (üç tane on):

Eski Krallık'tan prenses 'nin Giza'daki mezarında bulunan dikili taş levha (MÖ 2590-2565), kireçtaşı üzerine resim, şimdi Louvre Müzesindedir.

Mısır rakamları, Hanedanlık Öncesi döneme kadar uzanmaktadır. Abydos'un fildişi etiketleri bu sayı sisteminin kullanımını kaydeder. Adak öğelerin sayısını belirtmek için adak sahnelerinde sayıları görmek de yaygındır. Kralın kızı Neferetiabet'e 1000 öküz, ekmek, bira vb.

Mısır sayı sistemi eklemeliydi. Büyük sayılar, kabartma koleksiyonlarıyla temsil edildi ve değer, tek tek sayıların bir araya getirilmesiyle elde edildi.

Bu sahne bir sığır sayısını tasvir etmektedir (Mısırbilimci Lepsius tarafından kopyalanmıştır). Ortadaki kayıtta solda 835 boynuzlu sığır görüyoruz, hemen arkasında 220 hayvan (inek?) ve sağda 2235 keçi var. En alttaki kayıtta solda 760 eşek ve sağda 974 keçi görüyoruz.

Mısırlılar neredeyse yalnızca 1/n biçimindeki kesirleri kullandılar. Dikkate değer bir istisna, matematiksel metinlerde sıklıkla bulunan 2/3 kesiridir. Çok nadiren 3/4'ü belirtmek için özel bir kabartma kullanıldı. 1/2 kesiri, ikiye katlanmış bir keten parçasını tasvir etmiş olabilecek bir kabartma ile temsil edildi. 2/3 kesiri, 2 (farklı boyutta) vuruş ve bir ağızla tasvir eden bir kabartma ile temsil edildi. Kesirlerin geri kalanı her zaman bir sayının üzerine birleştirilmiş bir ağızla temsil edildi.

${\displaystyle 1/2}$ !! ${\displaystyle 1/3}$ !! ${\displaystyle 2/3}$ !! ${\displaystyle 1/4}$ !! ${\displaystyle 1/5}$!!${\displaystyle 3/4}$

Rhind Papirüsü'nden kesir yazma örneği:

5 + ¹⁄₂ + ¹⁄₇ + ¹⁄₁₄ (= 5 ⁵⁄₇)

Aritmetik

Toplama ve çıkarma

Rhind (Ahmes) Papirüsü'nde (yaklaşık MÖ 1550) ekleme ya da çıkarma için kullanılan hiyeroglif gösterilmektedir:

veya

Bu hiyeroglifin "bacaklarının" yönü yazı yönüyle örtüşüyorsa (Mısırlılar genellikle sağdan sola yazıyordu), o zaman "toplama", aksi takdirde "çıkarma" anlamına geliyordu. Ancak, Moskova Matematik Papirüsünde (MÖ 1850), çizginin sonuna doğru yönlendirilmiş bir çift bacak sayısının karesi anlamına geliyordu.

Toplama ondan büyük bir sayı ile sonuçlanırsa, yükselen bir hiyeroglifte on yazılır.

Örneğin: 2343 + 1671

+

Tüm aynı tür hiyeroglifleri bir araya topluyoruz ve şunları elde ediyoruz:

Hadi dönüşelim:

Nihai sonuç şuna benzer:

Çarpma ve bölme

Mısır çarpımı, Eski Krallığa bağlanan bir yöntemle, çarpılacak sayının (çarpılan) tekrar tekrar ikiye katlanması ve ikiye katlamalardan hangisinin toplanacağının seçilmesiyle (esasen bir ikili aritmetik biçimi) yapıldı. Çarpılan, şekil 1'in yanına yazılmıştır; çarpan daha sonra kendisine eklendi ve sonuç 2 sayısının yanına yazıldı. İşlem, ikiye katlama çarpanın yarısından büyük bir sayı verene kadar sürdürüldü. Ardından, iki katına çıkan sayılar (1, 2, vb.), cevabı oluşturmak için mevcut hesaplamaların sonuçlarından hangisinin bir araya getirilmesi gerektiğini seçmek için çarpandan tekrar tekrar çıkarılır.

Daha büyük sayılar için kısa bir yol olarak, çarpılan da hemen 10, 100, 1000, 10000 vb. ile çarpılabilir.

Örneğin, Rhind Papirüsü (RMP) üzerindeki Problem 69, (RMP'nin gerçek hiyeratik yazısı yerine) Hiyeroglif semboller kullanılmış gibi temsil edilirse aşağıdaki çizimi sağlar.

80 × 14 işleminin sonucunu hesaplamak
Eski Mısır hesabı			Modern hesap
Sonuç	Çarpan		Sonuç	Çarpan
			80	1
			800	10
			160	2
			320	4
			1120	14

, nihai cevabı üretmek için bir araya getirilen ara sonuçları gösterir.

Yukarıdaki tablo, 1120'yi 80'e bölmek için de kullanılabilir. Bu sorunu, toplamı 1120'ye ulaşan 80'in çarpanlarının toplamı olarak bölümü (80) bularak çözerdik. Bu örnekte, 10 + 4 = 14 bölümü verir. Bölme algoritmasının daha karmaşık bir örneği Problem 66 tarafından sağlanmıştır. Toplam 3200 ro yağ, 365 günde eşit olarak dağıtılacaktır.

3200'yi 365'e bölmek

1	365
2	730
4	1460
8	2920
2/3	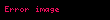${\displaystyle 243{\tfrac {1}{3}}}$
1/10	${\displaystyle 36{\tfrac {1}{2}}}$
1/2190	${\displaystyle {\tfrac {1}{6}}}$

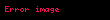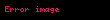
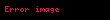
İlk olarak, yazar 365'in olası en büyük katına ulaşılıncaya kadar art arda ikiye katlar, ki bu 3200'den küçüktür. Bu durumda 8 kere 365, 2920'dir ve 365'in katlarının daha fazla eklenmesi açıkça 3200'den daha büyük bir değer verecektir. ${\displaystyle (2/3+1/10+1/2190)}$ çarpı 365'in bize ihtiyacımız olan 280 değerini verdiğini kaydetti. Dolayısıyla, 3200'ün 365'e bölünmesinin ${\displaystyle 8+2/3+1/10+1/2190}$'a eşit olması gerektiğini buluyoruz.

Cebir

Mısır cebir problemleri hem Rhind Papirüsünde hem de Moskova Papirüsünde ve diğer bazı kaynaklarda görülmektedir.

Hiyeroglif olarak: Aha

Aha problemleri, miktarı ve parçalarının toplamı verildiğinde bilinmeyen miktarları (Aha olarak anılır) bulmayı içerir. Rhind Papirüsü ayrıca bu tür problemlerden dördünü içerir. Moskova Papirüsünün 1., 19. ve 25. problemleri, Aha problemidir. Örneğin problem 19, birinden 1 ve 1⁄2 kez alınan ve 10 yapmak için 4'e eklenen bir miktarın hesaplamasını ister. Başka bir deyişle, modern matematiksel gösterimde aşağıdaki doğrusal denklemi çözmemiz istenir:

${\displaystyle {\frac {3}{2}}\times x+4=10.\ }$

Bu Aha problemlerini çözmek, sabit kesen yöntemi (regula falsi) adı verilen bir tekniği içerir. Bu teknik aynı zamanda yanlış varsayım yöntemi olarak da adlandırılır. Yazıcı, problemin cevabının ilk tahminini değiştirir. Yanlış varsayımı kullanan çözüm, gerçek yanıtla orantılı olacak ve yazar bu oranı kullanarak yanıtı bulacaktır.

Matematiksel yazılar, yazarların kesirli problemleri tam sayı kullanan problemlere dönüştürmek için (en az) ortak katları kullandığını göstermektedir. Bu bağlamda kesirlerin yanına kırmızı yardımcı numaralar yazılır.

Horus göz kesirlerinin kullanımı, geometrik ilerleme hakkında bazı (ilkel) bilgileri gösterir. Aritmetik ilerlemelerin bilgisi, matematiksel kaynaklardan da apaçık anlaşılmaktadır.

İkinci dereceden denklemler

Eski Mısırlılar, ikinci dereceden (kuadratik) denklemleri geliştiren ve çözen ilk uygarlıktı. Bu bilgi Berlin Papirüs parçasında bulunur. Ayrıca Mısırlılar, Rhind Papirüsü'nde bulunan birinci derece cebirsel denklemleri de çözmüşlerdir.

Geometri

Moskova Papirüsü'nden Problem 14'ün görüntüsü. Problem, kesik piramidin boyutlarını gösteren bir çizim içerir.

Antik Mısır'dan geometri ile ilgili yalnızca sınırlı sayıda problem vardır. Geometrik problemler hem Moskova Papirüsünde (MMP-Moscow Mathematical Papyrus) hem de Rhind Papirüsünde (RMP) ortaya çıkar. Örnekler, Eski Mısırlıların birkaç geometrik şeklin alanlarını, silindir ve piramit hacimlerini nasıl hesaplayacaklarını bildiklerini gösteriyor.

• Alan:
  • Üçgenler: Yazarlar, bir üçgenin alanını hesaplayan problemleri kaydeder (RMP ve MMP).
  • Dikdörtgenler: Dikdörtgen bir arazi parçasının alanıyla ilgili problemler RMP ve MMP'de görülmektedir. Benzer bir problem, Londra'daki 'nde yer almaktadır.
  • Daireler: RMP'nin Problem 48'i bir dairenin alanını (bir sekizgen ile yakınsayarak) ve çevreleyen kareyi karşılaştırmaktadır. Bu problemin sonucu, yazarın 9 khet çapında yuvarlak bir alanın alanını bulduğu problem 50'de kullanılır.
  • Yarımküre: MMP'deki Problem 10, bir yarım kürenin alanını buluyor.

Mısırlılar geometri alanında bir dikdörtgen, üçgen ve yamuk alanı için kesin formülleri biliyorlardı. Kenarları a, b, c, d olan keyfi bir dörtgenin alanı yaklaşık olarak şu şekilde hesaplandı: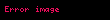${\displaystyle S={\frac {a+c}{2}}\cdot {\frac {b+d}{2}}}$; Bu kaba formül, şekil bir dikdörtgene yakınsa kabul edilebilir kesinlik sağlar.

Mısırlılar, çapı d olan bir S çemberinin alanının, kenarı çapın 8/9'u olan bir karenin alanına eşit olduğunu varsaydılar: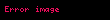${\displaystyle S=\left(d-{\frac {d}{9}}\right)^{2}=\left({\frac {8}{9}}d\right)^{2}.}$ Bu kural, ${\displaystyle \pi \approx 4\cdot \left({\frac {8}{9}}\right)^{2}}$ ≈ 3,1605 yaklaşımına karşılık gelir. (% 1'den az hata).

Moskova Matematik Papirüsünün 10. problemine dayanan bazı araştırmacılar, Mısırlıların bir kürenin alanını hesaplamak için kesin formülü bildiklerine inanıyordu, ancak diğer bilim adamları buna katılmıyorlar.

• Hacimler:
  • Silindirik tahıl ambarları: Birkaç problem silindirik tahıl ambarlarının (RMP 41-43) hacmini hesaplarken, RMP Problem 60, bir piramit yerine bir sütun veya bir koni ile ilgili görünmektedir. Oldukça küçük ve diktir, dört avuç içi (her kübit başına) seke (eğimin tersi).'nün IV.3 bölümünde bir Dairesel tabanlı tahıl ambarı, RMP 43 ile aynı prosedürü kullanarak bulunur.
  • Dikdörtgen tahıl ambarları: Moskova Papirüsü (Problem 14) ve Rhind Papirüsü'nde çeşitli problemler (44, 45, 46) dikdörtgen bir tahıl ambarının hacmi ile ilgilidir.
  • Kesik piramit (frustum): Kesik bir piramidin hacmi MMP 14'te hesaplanır.

Mısırlılar paralel yüzlü, silindir, koni ve piramitlerin hacimlerini hesaplayabilirlerdi. Mısırlılar kesik piramidin hacmini hesaplamak için aşağıdaki kuralı kullandılar (Moskova Matematik Papirüsünün 14. Problemi): alt taban a, üst b ve h yüksekliğinin bir kenarı ile düzenli kesik bir piramide sahip olalım; daha sonra hacim aşağıdaki (doğru) formül kullanılarak hesaplandı:

${\displaystyle V=(a^{2}+ab+b^{2})\cdot {\frac {h}{3}}.}$

Oxyrinchus'ta bulunan eski bir papirüs parşömeni, Mısırlıların kesilmiş bir koninin hacmini de hesaplayabildiğini gösteriyor. Bu bilgiyi bir su saati yapmak için kullandılar. Örneğin, Amenhotep III tarafından Karnak'ta bir su saati yapıldığı biliniyor.

Oxyrhynch'deki çizimlere göre su saatinin yeniden yapılandırılması

Mısır Üçgeni

Mısır üçgeni, en boy oranı 3:4:5 olan dik açılı bir üçgendir. Birinci yüzyılda Plutarch, On Isis and Osiris adlı çalışmasında bu üçgen hakkında şunları yazdı: "Görünüşe göre Mısırlılar, Birliğin doğasını üçgenlerin en güzeliyle karşılaştırıyorlar." Belki de bu yüzden bu üçgene Mısırlı üçgen denilmiştir [14]. Nitekim Yunan bilim adamları, Mısır'da dik açı oluşturmak için 12 eş parçaya bölünmüş bir ipin kullanıldığını bildirdi.

Mısır üçgeni, örneğin piramitlerin inşasında Mısırlı araştırmacılar ve mimarlar tarafından dik açılar oluşturmak için aktif olarak kullanıldı. Tarihçi Van der Waerden bu gerçeği sorgulamaya çalıştı, ancak daha sonraki çalışmalar bunu doğruladı.

Seqed

RMP'nin 56. problemi, geometrik benzerlik fikrinin anlaşıldığını göstermektedir. Bu problem, seqed olarak da bilinen oranın uzanmasını/yükselişini tartışmaktadır. Piramitleri inşa etmek için böyle bir formüle ihtiyaç duyulacaktır. Bir sonraki problemde (Problem 57), bir piramidin yüksekliği, taban uzunluğu ve seked (eğimin tersi için kullanılan Mısır terimi) ile hesaplanırken, Problem 58 tabanın uzunluğunu ve yüksekliğini verir ve seqed'i hesaplamak için bu ölçümleri kullanır. Problem 59'da 1. kısım seqed'i hesaplarken, ikinci kısım cevabı kontrol etmek için bir hesaplama olabilir: Tabanı 12 [arşın] ve seqed'i 5 avuç içi 1 parmak olan bir piramit inşa ederseniz, yüksekliği nedir?

Ayrıca bakınız

• Matematik tarihi
  • Geometri tarihi
• Mısır hiyeroglifleri ve
• ve

Kaynakça

1. ^ ^{a b c d e} (2006). "Ancient Egyptian Mathematics: New Perspectives on Old Sources". The Mathematical Intelligencer. 28 (1): 19-27. doi:10.1007/bf02986998. 
2. ^ ^{a b c} Burton, David (2005). The History of Mathematics: An Introduction. McGraw–Hill. ISBN . 
3. ^ Rossi, Corinna (2007). Architecture and Mathematics in Ancient Egypt. Cambridge University Press. ISBN . 
4. ^ ^{a b c d e f g} Katz V, , , Dauben JW, Plofker K, Berggren JL (2007). The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. ISBN . 
5. ^ Reimer, David (11 Mayıs 2014). Count Like an Egyptian: A Hands-on Introduction to Ancient Mathematics (İngilizce). Princeton University Press. ISBN . 
6. ^ ^{a b c d e f g h i j k l m n o p q r s t u v w x} Clagett, Marshall Ancient Egyptian Science, A Source Book. Volume Three: Ancient Egyptian Mathematics (Memoirs of the American Philosophical Society) American Philosophical Society. 1999
7. ^ Gardiner Alan H. Egyptian grammar: being an introduction to the study of hieroglyphs 3rd ed., rev. London: 1957, s. 197.
8. ^ (1993). A History of Mathematical Notations. Dover Publications. ss. 229-230. ISBN . 
9. ^ Karpinski, Louis C., Algebraical Developments Among the Egyptians and Babylonians, The American Mathematical Monthly: journal, (1917), Vol. 24, No: 6, p.259., doi:10.2307/2973180, https://www.jstor.org/stable/2973180 14 Eylül 2020 tarihinde Wayback Machine sitesinde .
10. ^ Moore, Deborah Lela (1994). The African roots of mathematics (2. bas.). Detroit, Mich.: Professional Educational Services. ISBN . 
11. ^ ^{a b} Greeks Science Before the Greeks Science, New Series, Vol.73, No. 1831, (31 Ocak 1930), s. 109–121
12. ^ Digitalegypt web sitesi: Lahun Papyrus IV.3 26 Haziran 2012 tarihinde Wayback Machine sitesinde .
13. ^ ^{a b} History of Mathematics, Volume I 1970.
14. ^ WW Struve (1930). Mathematischer Papyrus des Museum in Moskau. Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, Abteilung A. Berlin: Springer. s. 157. 
15. ^ Van der Waerden BL Science awakening. The Mathematics of Ancient Egypt, Babylon and Greece, ss. 44-45
16. ^ (2013). "Chapter 1. Ancient Egypt and Babylon". History of Mathematics. (unpublished). s. 5. 28 Haziran 2020 tarihinde kaynağından . Erişim tarihi: 6 Eylül 2020. 

Konuyla ilgili yayınlar

• Boyer, Carl B. 1968. History of Mathematics. John Wiley. Reprint Princeton U. Press (1985).
• Chace, Arnold Buffum. 1927–1929. The Rhind Mathematical Papyrus: Free Translation and Commentary with Selected Photographs, Translations, Transliterations and Literal Translations. 2 vols. Classics in Mathematics Education 8. Oberlin: Mathematical Association of America. (Reprinted Reston: National Council of Teachers of Mathematics, 1979).
• Clagett, Marshall. 1999. Ancient Egyptian Science: A Source Book. Volume 3: Ancient Egyptian Mathematics. Memoirs of the American Philosophical Society 232. Philadelphia: American Philosophical Society.
• Couchoud, Sylvia. 1993. Mathématiques égyptiennes: Recherches sur les connaissances mathématiques de l'Égypte pharaonique. Paris: Éditions Le Léopard d'Or
• Daressy, G. "Ostraca," Cairo Museo des Antiquities Egyptiennes Catalogue General Ostraca hieraques, vol 1901, number 25001-25385.
• Gillings, Richard J. 1972. Mathematics in the Time of the Pharaohs. MIT Press. (Dover reprints available).
• . 2003. "Ägyptische Algorithmen". Wiesbaden: Harrassowitz
• Johnson, G., Sriraman, B., Saltztstein. 2012. "Where are the plans? A socio-critical and architectural survey of early Egyptian mathematics"| In , Editor. Crossroads in the History of Mathematics and Mathematics Education. Monographs in Mathematics Education 12, Information Age Publishing, Inc., Charlotte, NC
• Neugebauer, Otto (1969) [1957]. The Exact Sciences in Antiquity (2 bas.). Dover Publications. ISBN . 14 Ağustos 2020 tarihinde kaynağından . Erişim tarihi: 6 Eylül 2020. 
• Peet, Thomas Eric. 1923. The Rhind Mathematical Papyrus, British Museum 10057 and 10058. London: The University Press of Liverpool limited and Hodder & Stoughton limited
• Reimer, David (2014). Count Like an Egyptian: A Hands-on Introduction to Ancient Mathematics. Princeton, NJ: Princeton University Press. ISBN . 
• Robins, R. Gay. 1995. "Mathematics, Astronomy, and Calendars in Pharaonic Egypt". In Civilizations of the Ancient Near East, edited by Jack M. Sasson, John R. Baines, Gary Beckman, and Karen S. Rubinson. Vol. 3 of 4 vols. New York: Charles Schribner's Sons. (Reprinted Peabody: Hendrickson Publishers, 2000). 1799–1813
• Robins, R. Gay, and Charles C. D. Shute. 1987. The Rhind Mathematical Papyrus: An Ancient Egyptian Text. London: British Museum Publications Limited.
• Sarton, George. 1927. Introduction to the History of Science, Vol 1. Willians & Williams.
• Strudwick, Nigel G., and Ronald J. Leprohon. 2005. Texts from the Pyramid Age. Brill Academic Publishers. .
• Struve, Vasilij Vasil'evič, and Boris Aleksandrovič Turaev. 1930. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau. Quellen und Studien zur Geschichte der Mathematik; Abteilung A: Quellen 1. Berlin: J. Springer
• Van der Waerden, B.L. 1961. Science Awakening". Oxford University Press.
• Vymazalova, Hana. 2002. Wooden Tablets from Cairo...., Archiv Orientalni, Vol 1, pages 27–42.
• Wirsching, Armin. 2009. Die Pyramiden von Giza – Mathematik in Stein gebaut. (2. bas.) Books on Demand. .

Dış bağlantılar

• . 10 Nisan 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Şubat 2021.  (Mısır Aritmetiği)
• . 6 Kasım 2013 tarihinde kaynağından arşivlendi.