Eşyapı ya da izomorfizma (ya da izomorfi), aynı kategoride(grupta) olan benzer iki matematiksel obje arasında bir gönderim olup matematiksel vücut tersi yapıda da muhafaza edilir. Aralarında bu şekilde eşyapı bulunan objelere eşyapısal ya da izomorf(ik) objeler denir. Örneğin iki küme arasında eşyapı, birebir, örten bir gönderimdir. Kümelerin üzerinde elemanlara sahip olma haricinde bir oluşum olmadığından, eşyapı gönderiminin koruyacağı başka bir yapı yoktur. iki grup arasında bir eşyapı, birebir, örten bir gönderimdir; dahası, iki gruptaki işleme saygı gösterir, bu iki işlemin birbirleriyle etkileşim halinde olmasını sağlar.
Ludwig Von Bertalanffy'e göre genel sistem özelliklerinin varoluşunun bir sonucu, farklı alanlardaki (disiplinlerdeki) yapısal benzerlik ya da izomorfizmlerin ortaya çıkışıdır. Özünde oldukça farklı olan bireylerin davranışını yöneten prensiplerde uyumlulukların olduğu tespit edilmiştir. Basit bir örneği ele alırsak, büyümenin üstsel bir kanunu belirli bakteriyel hücrelere, bakteri, hayvan ya da insan popülasyonlarına ve genel olarak bilimde veya genetik alanındaki yayınların sayısıyla ölçülen bilimsel araştırmanın gelişimine uygulanabilmektedir.
Ayrıca sistem izomorfizmleri sayısal analizlere direnen ama buna rağmen büyük içsel bir ilgiye sahip olan problemlerde de karşımıza çıkmaktadır. Örnek verilecek olursa; hayvan toplulukları ve insan toplumları gibi biyolojik sistemler ve kolonisel organizmalar arasında izomorfizmler bulunmaktadır. Birçok durumda, izomorfik kanunlar varlıkların doğası göz önüne alınmaksızın sistemlerin belirli sınıf veya altsınıflarda geçerlidirler. Bu yüzden tartışılmakta olan "izomorfizm" kavramı, benzerlik anlamındaki "analoji"den çok daha fazla anlama sahiptir.
Aşağıdaki örneklere bakınız.
Eşyapılar, Cebir, Kategori Teorisi, Model Teorisi, Topoloji gibi alanların, inşa ettikleri nesneleri sınıflandırmada, tıpkılıklarını fark etmede, doğal olarak karşılarına çıkan kavramlardır. Bu nesneleri, üzerlerinde tanımladıkları yapılar bağlamında incelerken eşyapısal nesneleri birbirlerine denk tutarlar.
Tanım
En geniş tanımıyla, bir 


















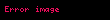
Yani 

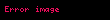

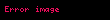


Örnekler
- : İki küme arasında bir gönderim birebir ve örtense (yani ise) bu gönderim kümeler kategorisinde bir eşyapıdır. İki küme arasında eşyapı varsa, kümeler kuramı içinde kümelerden biri için kanıtlanmış bir gerçek diğeri için de doğrudur. Dolayısıyla, kümeler kuramında bu iki küme denk olarak düşünülür. Örneğin resmi bir voleybol oyunu sırasında sahadaki oyuncuların kümesiyle, bir yıl içinde ayların kümesi eşyapısaldır (ikisinde de 12 eleman var). Ayrıca tüm kesirli sayılar kümesiyle tüm tam sayılar kümesi eşyapısaldır. Oysa tüm kesirli sayılar kümesiyle tüm gerçel sayılar kümesi eşyapısal olamazlar (bkz. Cantor'un köşegen yöntemi).
- : (
,
) ve
,
iki grup olsun.
ve
birer küme olduğundan, aralarında bir
grup eşyapısı öncelikle ilk örnekte olduğu gibi birebir bir eşleme olmalıdır. Ayrıca, bu gönderim
ve
üzerindeki işlemleri korumalıdır, birini diğerine götürmelidir. Bunu söylerken tam tamına şu özdeşlik kastedilir:
ve
'da iki eleman olmak üzere her
ve
için
.
Yanive
'yi
'da işleme sokup
'ye göndermek,
'ye gönderip imgeleri oradaki işleme sokmakla her zaman aynı sonucu vermeli.
- : (
) ve
iki halka olsun.
'dan B'ye bir halka eşyapısı birebir bir eşlemedir ve halka yapılarını korur:
ve
'da herhangi iki eleman olmak üzere
ve
.
- Doğrusal cebirde: İki vektör uzayı arasında bir vektör uzayı eşyapısı, birebir bir eşlemedir ve uzaylardaki vektör toplama işlemini ve ölçeksel çarpmayı yukarıdaki anlamda korur. Sonlu boyutlu iki vektör uzayının boyutları aynıysa, gösterilebilir ki bu uzaylar eşyapısaldır.
- Çizge kuramında:
ve
iki çizge olsun.
'nın ve
'nin köşelerinin oluşturduğu kümeleri sırasıyla
ve
olarak gösterelim.
'dan
'ye bir çizge eşyapısı,
'dan
'ye birebir bir eşlemedir; ayrıca bu eşleme,
'da (birbirlerine bir kenarla) bağlı iki köşeyi,
'de bağlı iki köşeye götürmelidir ve eğer iki köşenin
'deki imgeleri bağlıysa
'da da bağlı olmalıdır. Dolayısıyla bir çizge eşyapısı, kenarları koruyan birebir bir eşlemedir.
- Topolojide: İki topolojik uzay arasında bir topolojik eşyapı, kendisi ve tersi sürekli olan birebir bir eşlemedir. İki çokkatlı arasında bir eşyapı, kendisi ve tersi türevlenebilir birebir bir eşlemedir.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Esyapi ya da izomorfizma ya da izomorfi ayni kategoride grupta olan benzer iki matematiksel obje arasinda bir gonderim olup matematiksel vucut tersi yapida da muhafaza edilir Aralarinda bu sekilde esyapi bulunan objelere esyapisal ya da izomorf ik objeler denir Ornegin iki kume arasinda esyapi birebir orten bir gonderimdir Kumelerin uzerinde elemanlara sahip olma haricinde bir olusum olmadigindan esyapi gonderiminin koruyacagi baska bir yapi yoktur iki grup arasinda bir esyapi birebir orten bir gonderimdir dahasi iki gruptaki isleme saygi gosterir bu iki islemin birbirleriyle etkilesim halinde olmasini saglar Ludwig Von Bertalanffy e gore genel sistem ozelliklerinin varolusunun bir sonucu farkli alanlardaki disiplinlerdeki yapisal benzerlik ya da izomorfizmlerin ortaya cikisidir Ozunde oldukca farkli olan bireylerin davranisini yoneten prensiplerde uyumluluklarin oldugu tespit edilmistir Basit bir ornegi ele alirsak buyumenin ustsel bir kanunu belirli bakteriyel hucrelere bakteri hayvan ya da insan populasyonlarina ve genel olarak bilimde veya genetik alanindaki yayinlarin sayisiyla olculen bilimsel arastirmanin gelisimine uygulanabilmektedir Ayrica sistem izomorfizmleri sayisal analizlere direnen ama buna ragmen buyuk icsel bir ilgiye sahip olan problemlerde de karsimiza cikmaktadir Ornek verilecek olursa hayvan topluluklari ve insan toplumlari gibi biyolojik sistemler ve kolonisel organizmalar arasinda izomorfizmler bulunmaktadir Bircok durumda izomorfik kanunlar varliklarin dogasi goz onune alinmaksizin sistemlerin belirli sinif veya altsiniflarda gecerlidirler Bu yuzden tartisilmakta olan izomorfizm kavrami benzerlik anlamindaki analoji den cok daha fazla anlama sahiptir Asagidaki orneklere bakiniz Esyapilar Cebir Kategori Teorisi Model Teorisi Topoloji gibi alanlarin insa ettikleri nesneleri siniflandirmada tipkiliklarini fark etmede dogal olarak karsilarina cikan kavramlardir Bu nesneleri uzerlerinde tanimladiklari yapilar baglaminda incelerken esyapisal nesneleri birbirlerine denk tutarlar TanimEn genis tanimiyla bir K displaystyle K kategorisi icinde iki nesne A displaystyle A ve B displaystyle B ve A displaystyle A dan B displaystyle B ye kategorinin bir gonderimi f displaystyle f var olsun Eger f displaystyle f nin ayni kategoride izin verilen gonderimler icinde bir tersi varsa bu ters g displaystyle g olsun ve gf brA displaystyle gf br A ve fg brB displaystyle fg br B esitlikleri saglaniyorsa f displaystyle f ye A displaystyle A dan B displaystyle B ye bir esyapi gonderimi denir Tabii ki g displaystyle g de B displaystyle B den A displaystyle A ya bir esyapi gonderimi olur Burada brA displaystyle br A olarak gosterilen gonderim A displaystyle A da her bir elemani kendisine goturen gonderimdir f displaystyle f esyapisinin tersi olan gonderim f 1 displaystyle f 1 olarak gosterilir Yani f displaystyle f bir esyapiysa ayni kategoride bir de tersi vardir ve once f displaystyle f ile gidip sonra f 1 displaystyle f 1 ile geri donunce A displaystyle A da hicbir sey yapmamis oluruz benzer bicimde once f 1 displaystyle f 1 ile gidip sonra f displaystyle f ile geri donunce B displaystyle B de hicbir sey yapmayiz Ornekler Iki kume arasinda bir gonderim birebir ve ortense yani ise bu gonderim kumeler kategorisinde bir esyapidir Iki kume arasinda esyapi varsa kumeler kurami icinde kumelerden biri icin kanitlanmis bir gercek digeri icin de dogrudur Dolayisiyla kumeler kuraminda bu iki kume denk olarak dusunulur Ornegin resmi bir voleybol oyunu sirasinda sahadaki oyuncularin kumesiyle bir yil icinde aylarin kumesi esyapisaldir ikisinde de 12 eleman var Ayrica tum kesirli sayilar kumesiyle tum tam sayilar kumesi esyapisaldir Oysa tum kesirli sayilar kumesiyle tum gercel sayilar kumesi esyapisal olamazlar bkz Cantor un kosegen yontemi A displaystyle A displaystyle circ ve B displaystyle B displaystyle iki grup olsun A displaystyle A ve B displaystyle B birer kume oldugundan aralarinda bir f displaystyle f grup esyapisi oncelikle ilk ornekte oldugu gibi birebir bir esleme olmalidir Ayrica bu gonderim A displaystyle A ve B displaystyle B uzerindeki islemleri korumalidir birini digerine goturmelidir Bunu soylerken tam tamina su ozdeslik kastedilir x displaystyle x ve y displaystyle y A displaystyle A da iki eleman olmak uzere her x displaystyle x ve y displaystyle y icin f x displaystyle f x displaystyle circ y f x displaystyle y f x displaystyle f y displaystyle f y Yani x displaystyle x ve y displaystyle y yi A displaystyle A da isleme sokup B displaystyle B ye gondermek B displaystyle B ye gonderip imgeleri oradaki isleme sokmakla her zaman ayni sonucu vermeli A displaystyle A displaystyle circ ve B displaystyle B displaystyle cdot iki halka olsun A displaystyle A dan B ye bir halka esyapisi birebir bir eslemedir ve halka yapilarini korur x displaystyle x ve y displaystyle y A displaystyle A da herhangi iki eleman olmak uzere f x displaystyle f x displaystyle y f x displaystyle y f x displaystyle cdot f y displaystyle f y ve f x displaystyle f x displaystyle circ y f x displaystyle y f x displaystyle f y displaystyle f y Dogrusal cebirde Iki vektor uzayi arasinda bir vektor uzayi esyapisi birebir bir eslemedir ve uzaylardaki vektor toplama islemini ve olceksel carpmayi yukaridaki anlamda korur Sonlu boyutlu iki vektor uzayinin boyutlari ayniysa gosterilebilir ki bu uzaylar esyapisaldir Cizge kuraminda A displaystyle A ve B displaystyle B iki cizge olsun A displaystyle A nin ve B displaystyle B nin koselerinin olusturdugu kumeleri sirasiyla KA displaystyle K A ve KB displaystyle K B olarak gosterelim A displaystyle A dan B displaystyle B ye bir cizge esyapisi KA displaystyle K A dan KB displaystyle K B ye birebir bir eslemedir ayrica bu esleme A displaystyle A da birbirlerine bir kenarla bagli iki koseyi B displaystyle B de bagli iki koseye goturmelidir ve eger iki kosenin B displaystyle B deki imgeleri bagliysa A displaystyle A da da bagli olmalidir Dolayisiyla bir cizge esyapisi kenarlari koruyan birebir bir eslemedir Topolojide Iki topolojik uzay arasinda bir topolojik esyapi kendisi ve tersi surekli olan birebir bir eslemedir Iki cokkatli arasinda bir esyapi kendisi ve tersi turevlenebilir birebir bir eslemedir
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans