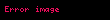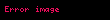Gauss integrali, Euler–Poisson integrali olarak da bilinir, tüm reel sayılardaki e−x2Gauss fonksiyonunun integralidir. Alman matematik ve fizikçi Carl Friedrich Gauss'dan sonra adlandırlıdı. İntegrali şöyledir:
Bu integral çok geniş uygulama alanına sahiptir. Örneğin değişkenlerin azıcık değiştirilerek normal dağılımın normalleştirme sabitini hesaplamak için kullanılır. Sonlu sınırları olan aynı integral, normal dağılımın hem hem de birikimli dağılım fonksiyonu ile yakından ilişkilidir.
Hata fonksiyonu için her ne kadar temel fonksiyon olmazsa bile, kanıtlamıştır ki, Kalkülüs araçları kullanılarak Gauss integrali analitik olarak çözülebilir. Burada, aşağıdaki integralin temel İlkel fonksiyonu yoktur:
fakat aşağıdaki belirli integrali hesaplanabilir:
Gauss integrali ile, fizikte çok sık karşılaşılır ve integralin sayısal genelleştirilmesi ile kuantum alan kuramında sık karşılaşılır.
Hesaplama
Kutupsal koordinat sisteminde
Gauss integralini hesaplamanın standart yolu Poisson'a geri gitmektir, is
- R2 düzleminde e−(x2 + y2) = e−r2 fonksiyonunu göz önüne alalım ve iki yolla integralini hesaplayalim:
- bir taraftan, bir kare integral olan kartezyen koordinat sistemindeki ile:
- diğer taraftan (kutupsal koordinat sistemindeki çift katlı integral) ile, bu integral π olarak hesaplar.
- bir taraftan, bir kare integral olan kartezyen koordinat sistemindeki ile:
Bu iki hesaplama karşılaştırılırsa uygun integral elde edilmiş olur.
Basit ispat
Kısaca yukarıdaki yöntem kullanılarak, bir taraftan şöyle hesaplanabilir;
Diğer taraftan da şöyle hesaplanabilir;
Buradaki r faktörü, kutupsal koordinat dönüşümlerinden elde edilir. (r dr dθ, kutupsal koordinat sisteminde ifade edilen düzlemin standart ölçüsüdür [1]25 Aralık 2012 tarihinde Wayback Machine sitesinde arşivlendi.) ve s = −r2 yerine konulursa ds = −2r dr olur.
Bunları bir araya getirirsek
olur.
Böylece,
elde edilir.
Kapsamlı ispat
Katlı integrallerin uygunluğunu ve iki ifadenin eşitliğini doğrulamak için, aşağıdaki yaklaşım fonksiyonu ile başlayalım:
Eğer integral şöyle olursa:
limiti şöyle olur;
Bu limit aşağıdaki integral ile uyuşur;
Bunun gerçek durumunu şöyledir;
Böylece şöyle hesaplayabiliriz
burada limit alınırsa
.
I(a)nın karesi elde edilir
kullanarak, yukarıdaki katlı integral, şu şekilde alan integraline çevrilebilir:
xy düzleminde {(−a, a), (a, a), (a, −a), (−a, −a)} köşelerine sahip bir kare elde edilir.
Üstel fonksiyon, tüm reel sayılar için 0'dan büyük olduğundan dolayı, karenin integrali 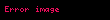
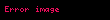
(Kutupsal dönüşümler için (kartezyen koordinatlardan kutupsal koordinatlara dönüşüme) bakın.)
Integral alma,
Sıkıştırma teoreminden, Gauss integral elde edilebilir:
Kartezyen koordinat sisteminde
Laplace dönüşümüne geri gitmenin farklı bir yöntemi, aşağıdaki gibidir:
y → ±∞ iken s sınırları, x in işaretine bağlıdır ve bir (çift fonksiyon) olan e−x2 kullanılarak hesaplama basitleştirilebilir. Böylece tüm reel sayılardaki integral için, sıfırdan sonsuza iki kez integral alınır. Bu da şöyle olur;
Böylece, x ≥ 0 için integral alınır ve y ile s değişkenleri aynı sınırlara sahiptir. Buradan:
elde edilir. Ardından:
Son olarak, 
Gama fonksiyonu ile ilişkisi
Bir (çift fonksiyonun) integrali şöyle olsun:
Burada 
Buradaki Γ, gama fonksiyonudur. Bu, bir yarım tam sayı faktöriyelinin, 
Genelleştirmeler
Gauss fonksiyonunun integrali
Keyfi bir Gauss fonksiyonunun integrali şöyledir:
Bunun başka bir biçimi de şöyledir:
n boyutlu ve fonksiyonel genelleştirme
A, bir simetrik pozitif tanımlı (bu yüzden tersinir) n×n ortak değişirli matrisi olsun. Böylece integral şöyle olur:
Burada integral Rnde anlaşılır. Bu, çokdeğişirli normal dağılım incelenerek uygulanır.
Ayrıca,
Burada σ, bir {1, ..., 2N} permütasyonu ve sağ taraftaki ek faktör, N nin {1, ..., 2N} tüm kombinasyonel çiftlerinin toplamıdır ve Ad−1'den elde edilmişlerdir.
Alternatif olarak,
Yüksek dereceli polinomlar
Diğer çift polinomların üstelleri seriler kullanılarak kolayca çözülebilir. Örneğin bir dördüncü dereceden bir polinomun üstel integralinin çözümü şöyledir:
Burada n + p = 0 mod 2 gereklidir. Çünkü −∞'dan 0'a integral her bir terimde (−1)n+p/2 faktörü oluştururken, 0'dan +∞'a integral her bir terimde 1/2 faktörü oluşturur. Bu integraller, kuantum alan kuramının konusuna girer.
Kaynakça
- ^ Пуассона интеграл 28 Ağustos 2009 tarihinde Wayback Machine sitesinde .
- ^ a b (PDF). 10 Ekim 2012 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 22 Şubat 2013.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Gauss integrali Euler Poisson integrali olarak da bilinir tum reel sayilardaki e x2Gauss fonksiyonunun integralidir Alman matematik ve fizikci Carl Friedrich Gauss dan sonra adlandirlidi Integrali soyledir e x2dx p displaystyle int infty infty e x 2 dx sqrt pi Bu integral cok genis uygulama alanina sahiptir Ornegin degiskenlerin azicik degistirilerek normal dagilimin normallestirme sabitini hesaplamak icin kullanilir Sonlu sinirlari olan ayni integral normal dagilimin hem hem de birikimli dagilim fonksiyonu ile yakindan iliskilidir Hata fonksiyonu icin her ne kadar temel fonksiyon olmazsa bile kanitlamistir ki Kalkulus araclari kullanilarak Gauss integrali analitik olarak cozulebilir Burada asagidaki integralin temel Ilkel fonksiyonu yoktur e x2dx displaystyle int e x 2 dx fakat asagidaki belirli integrali hesaplanabilir e x2dx displaystyle int infty infty e x 2 dx Gauss integrali ile fizikte cok sik karsilasilir ve integralin sayisal genellestirilmesi ile kuantum alan kuraminda sik karsilasilir HesaplamaKutupsal koordinat sisteminde Gauss integralini hesaplamanin standart yolu Poisson a geri gitmektir is R2 duzleminde e x2 y2 e r2 fonksiyonunu goz onune alalim ve iki yolla integralini hesaplayalim bir taraftan bir kare integral olan kartezyen koordinat sistemindeki ile e x2dx 2 displaystyle left int e x 2 dx right 2 diger taraftan kutupsal koordinat sistemindeki cift katli integral ile bu integral p olarak hesaplar Bu iki hesaplama karsilastirilirsa uygun integral elde edilmis olur Basit ispat Kisaca yukaridaki yontem kullanilarak bir taraftan soyle hesaplanabilir R2e x2 y2 dA e x2 y2 dxdy e x2dx e y2dy e x2dx 2 displaystyle int mathbf R 2 e x 2 y 2 dA int infty infty int infty infty e x 2 y 2 dx dy left int infty infty e x 2 dx right left int infty infty e y 2 dy right left int infty infty e x 2 dx right 2 Diger taraftan da soyle hesaplanabilir R2e x2 y2 dA 02p 0 e r2rdrd8 2p 0 re r2dr 2p 012esdss r2 p 0esds p e0 e p displaystyle begin aligned int mathbf R 2 e x 2 y 2 dA amp int 0 2 pi int 0 infty e r 2 r dr d theta amp 2 pi int 0 infty re r 2 dr amp 2 pi int infty 0 tfrac 1 2 e s ds amp amp s r 2 amp pi int infty 0 e s ds amp pi e 0 e infty amp pi end aligned Buradaki r faktoru kutupsal koordinat donusumlerinden elde edilir r dr d8 kutupsal koordinat sisteminde ifade edilen duzlemin standart olcusudur 1 25 Aralik 2012 tarihinde Wayback Machine sitesinde arsivlendi ve s r2 yerine konulursa ds 2r dr olur Bunlari bir araya getirirsek e x2dx 2 p displaystyle left int infty infty e x 2 dx right 2 pi olur Boylece e x2dx p displaystyle int infty infty e x 2 dx sqrt pi elde edilir Kapsamli ispat Katli integrallerin uygunlugunu ve iki ifadenin esitligini dogrulamak icin asagidaki yaklasim fonksiyonu ile baslayalim I a aae x2dx displaystyle I a int a a e x 2 dx Eger integral soyle olursa e x2dx displaystyle int infty infty e x 2 dx limiti soyle olur lima I a displaystyle lim a to infty I a Bu limit asagidaki integral ile uyusur e x2dx displaystyle int infty infty e x 2 dx Bunun gercek durumunu soyledir e x2 dx lt 1 xe x2dx 11e x2dx 1 xe x2dx lt displaystyle int infty infty e x 2 dx lt int infty 1 xe x 2 dx int 1 1 e x 2 dx int 1 infty xe x 2 dx lt infty Boylece soyle hesaplayabiliriz e x2dx displaystyle int infty infty e x 2 dx burada limit alinirsa lima I a displaystyle lim a to infty I a I a nin karesi elde edilir I a 2 aae x2dx aae y2dy aa aae y2dy e x2dx aa aae x2 y2 dxdy displaystyle begin aligned I a 2 amp left int a a e x 2 dx right left int a a e y 2 dy right amp int a a left int a a e y 2 dy right e x 2 dx amp int a a int a a e x 2 y 2 dx dy end aligned kullanarak yukaridaki katli integral su sekilde alan integraline cevrilebilir e x2 y2 d x y displaystyle int e x 2 y 2 d x y xy duzleminde a a a a a a a a koselerine sahip bir kare elde edilir Ustel fonksiyon tum reel sayilar icin 0 dan buyuk oldugundan dolayi karenin integrali I a 2 displaystyle I a 2 den kucuk olmalidir ve benzer sekilde karenin integrali de I a 2 displaystyle I a 2 den buyuk olmalidir Bu iki cemberin integralleri kutupsal koordinat donusumunden kolayca hesaplanabilir x rcos 8y rsin 8d x y rd r 8 displaystyle begin aligned x amp r cos theta y amp r sin theta d x y amp r d r theta end aligned 02p 0are r2drd8 lt I2 a lt 02p 0a2re r2drd8 displaystyle int 0 2 pi int 0 a re r 2 dr d theta lt I 2 a lt int 0 2 pi int 0 a sqrt 2 re r 2 dr d theta Kutupsal donusumler icin kartezyen koordinatlardan kutupsal koordinatlara donusume bakin Integral alma p 1 e a2 lt I2 a lt p 1 e 2a2 displaystyle pi 1 e a 2 lt I 2 a lt pi 1 e 2a 2 Sikistirma teoreminden Gauss integral elde edilebilir e x2dx p displaystyle int infty infty e x 2 dx sqrt pi Kartezyen koordinat sisteminde Laplace donusumune geri gitmenin farkli bir yontemi asagidaki gibidir y xsdy xds displaystyle begin aligned y amp xs dy amp x ds end aligned y iken s sinirlari x in isaretine baglidir ve bir cift fonksiyon olan e x2 kullanilarak hesaplama basitlestirilebilir Boylece tum reel sayilardaki integral icin sifirdan sonsuza iki kez integral alinir Bu da soyle olur e x2dx 2 0 e x2dx displaystyle int infty infty e x 2 dx 2 int 0 infty e x 2 dx Boylece x 0 icin integral alinir ve y ile s degiskenleri ayni sinirlara sahiptir Buradan I2 4 0 0 e x2 y2 dydx displaystyle I 2 4 int 0 infty int 0 infty e x 2 y 2 dy dx elde edilir Ardindan 14I2 0 0 e x2 y2 dy dx 0 0 e x2 1 s2 xds dx 0 0 e x2 1 s2 xdx ds 0 1 2 1 s2 e x2 1 s2 x 0x ds 12 0 ds1 s2 12 arctan s 0 p4 displaystyle begin aligned tfrac 1 4 I 2 amp int 0 infty left int 0 infty e x 2 y 2 dy right dx amp int 0 infty left int 0 infty e x 2 1 s 2 x ds right dx amp int 0 infty left int 0 infty e x 2 1 s 2 x dx right ds amp int 0 infty left frac 1 2 1 s 2 e x 2 1 s 2 right x 0 x infty ds amp tfrac 1 2 int 0 infty frac ds 1 s 2 amp tfrac 1 2 left arctan s frac right 0 infty amp tfrac pi 4 end aligned Son olarak I p displaystyle I sqrt pi olur Gama fonksiyonu ile iliskisiBir cift fonksiyonun integrali soyle olsun e x2dx 2 0 e x2dx displaystyle int infty infty e x 2 dx 2 int 0 infty e x 2 dx Burada x t displaystyle x sqrt t degisken degistirme yapilirsa bu denklem Euler integraline donusur 2 0 e x2dx 2 0 12 e t t 12dt G 12 p displaystyle 2 int 0 infty e x 2 dx 2 int 0 infty frac 1 2 e t t frac 1 2 dt Gamma left frac 1 2 right sqrt pi Buradaki G gama fonksiyonudur Bu bir yarim tam sayi faktoriyelinin p displaystyle sqrt pi nin bir oransal carpani oldugunu gosteriyor Bunun daha genel ifade soyledir 0 e axbdx 1b a 1bG 1b displaystyle int 0 infty e ax b dx frac 1 b a frac 1 b Gamma left frac 1 b right GenellestirmelerGauss fonksiyonunun integrali Keyfi bir Gauss fonksiyonunun integrali soyledir e x b 2c2dx cp displaystyle int infty infty e frac x b 2 c 2 dx c sqrt pi Bunun baska bir bicimi de soyledir e x2 bx cdx peb2 4 c displaystyle int infty infty e x 2 bx c dx sqrt pi e b 2 4 c n boyutlu ve fonksiyonel genellestirme A bir simetrik pozitif tanimli bu yuzden tersinir n n ortak degisirli matrisi olsun Boylece integral soyle olur exp 12 i j 1nAijxixj dnx exp 12xTAx dnx 2p ndetA displaystyle int infty infty exp left frac 1 2 sum i j 1 n A ij x i x j right d n x int infty infty exp left frac 1 2 x T Ax right d n x sqrt frac 2 pi n det A Burada integral Rnde anlasilir Bu cokdegisirli normal dagilim incelenerek uygulanir Ayrica xk1 xk2Nexp 12 i j 1nAijxixj dnx 2p ndetA12NN s S2N A 1 ks 1 ks 2 A 1 ks 2N 1 ks 2N displaystyle int x k 1 cdots x k 2N exp left frac 1 2 sum i j 1 n A ij x i x j right d n x sqrt frac 2 pi n det A frac 1 2 N N sum sigma in S 2N A 1 k sigma 1 k sigma 2 cdots A 1 k sigma 2N 1 k sigma 2N Burada s bir 1 2N permutasyonu ve sag taraftaki ek faktor N nin 1 2N tum kombinasyonel ciftlerinin toplamidir ve Ad 1 den elde edilmislerdir Alternatif olarak f x exp 12 i j 1nAijxixj dnx 2p ndetAexp 12 i j 1n A 1 ij xi xj f x x 0 displaystyle int f vec x exp left frac 1 2 sum i j 1 n A ij x i x j right d n x sqrt 2 pi n over det A left exp left 1 over 2 sum i j 1 n A 1 ij partial over partial x i partial over partial x j right f vec x right vec x 0 Yuksek dereceli polinomlar Diger cift polinomlarin ustelleri seriler kullanilarak kolayca cozulebilir Ornegin bir dorduncu dereceden bir polinomun ustel integralinin cozumu soyledir eax4 bx3 cx2 dx fdx 12ef n m p 0n p 0mod2 bnn cmm dpp G 3n 2m p 14 a 3n 2m p 14 displaystyle int infty infty e ax 4 bx 3 cx 2 dx f dx frac 1 2 e f sum begin smallmatrix n m p 0 n p 0 mod 2 end smallmatrix infty frac b n n frac c m m frac d p p frac Gamma left frac 3n 2m p 1 4 right a frac 3n 2m p 1 4 Burada n p 0 mod 2 gereklidir Cunku dan 0 a integral her bir terimde 1 n p 2 faktoru olustururken 0 dan a integral her bir terimde 1 2 faktoru olusturur Bu integraller kuantum alan kuraminin konusuna girer Kaynakca Puassona integral 28 Agustos 2009 tarihinde Wayback Machine sitesinde a b PDF 10 Ekim 2012 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 22 Subat 2013
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans