Matematikte kutupsal koordinat sistemi veya polar koordinat sistemi, birer açı ve Kartezyen koordinat sistemindeki orijinin eşdeğeri olup "kutup" olarak bilinen bir merkez noktaya olan uzaklıklar ile tanımlandığı, iki boyutlu bir koordinat sistemidir. Kutupsal koordinat sistemi, matematik, fizik, mühendislik, denizcilik, robot teknolojisi gibi birçok alanda kullanılır. Bu sistem, iki nokta arasındaki ilişkinin açı ve uzaklık ile daha kolay ifade edilebildiği durumlar için özellikle kullanışlıdır. Kartezyen koordinat sisteminde, böyle bir ilişki ancak trigonometrik formüller ile bulunabilir. Kutupsal denklemler, çoğu eğri tipi için en kolay, bazıları içinse yegâne tanımlama yöntemidir.

Tarihçe
Antik Yunan uygarlığı'nda açı ve yarıçap kavramlarının kullanıldığı bilinmektedir. (MÖ 190 - 120), her açı için uzunluklarını veren bir kiriş fonksiyonları tablosu oluşturulmuştur ve yıldızların konumlarını belirlemek için kutupsal koordinatlar kullandığına ilişkin kaynaklar bulunmaktadır. "Spiraller Üzerine" (On Spirals) adlı eserinde Arşimet, ünlü spiralini yarıçapın açıya bağlı olduğu bir fonksiyon olarak tanımlar. Bununla beraber, Yunan çalışmaları, koordinat sistemini tam olarak tanımlayamamıştır.
Kutupsal koordinatları resmî bir koordinat sisteminin parçası olarak ilk olarak kimin tanımladığına ilişkin farklı söylemler vardır. Konunun tarihçesi, Harvard profesörü 'in "Kutupsal Koordinatların Kaynağı" (Origin of Polar Coordinates) adlı kitabında anlatılmıştır. ve Bonaventura Cavalieri yaklaşık aynı zamanda birbirinden bağımsız olarak kavramları oluşturmaya başlamıştır. Saint-Vincent, çalışmalarını 1625 yılında yazmış ve 1647 yılında yayınlamışken, Cavalieri de 1635 yılında kendi çalışmalarının ilk baskısını yapıp 1653 yılında elden geçirilmiş bir sürümünü yayınlamıştır. Bir Arşimet spirali içindeki alanla ilgili bir problemin çözümünde kutupsal koordinat sisteminden ilk yararlanan Cavalieri olmuştur. Daha sonra Blaise Pascal, parabolik yayların uzunluğunu hesaplamak için kutupsal koordinatları kullanmıştır.
1671 yılında yazılmış ve 1736 yılında basılmış olan çalışmasıyla Isaac Newton, kutupsal koordinatlara bir düzlemdeki herhangi bir noktanın yerini saptama yöntemi olarak bakan ilk kişi olmuştur. Newton, kutupsal koordinatlar ve diğer dokuz koordinat sistemi arasındaki dönüşümleri incelemiştir. Acta eruditorum (1691) adlı çalışmasında Jacob Bernoulli, sırasıyla kutup ve kutupsal eksen olarak adlandırdığı bir nokta ve o noktanın üzerinde yer aldığı eksenden oluşan bir sistem kullanmıştır. Bu sistemde koordinatlar, kutba göre uzaklık ve kutup eksenine göre açı ile belirtilmiştir. Bernoulli'nin çalışması, bu koordinatlarla tanımlanmış eğrilerin eğim yarıçaplarını hesaplamaya kadar ilerlemiştir.
Gregorio Fontana'ya atfedilmiş olan kutupsal koordinatlar terimi, 18. yüzyıl İtalyan yazarları tarafından kullanılmıştır. Terimin İngilizce yayınlarda ilk yer alışı, 'ın 'ya ait "Diferansiyel ve İntegral Hesaplamalar" (Differential and Integral Calculus) adlı kitabını çevirmesi ile 1816 yılında olmuştur.
Alexis Clairaut ve Leonhard Euler, kutupsal koordinat kavramının üç boyuta uyarlanmasında rol oynamışlardır.
Kutupsal koordinatlar ile noktaların belirtilmesi

Tüm iki boyutlu koordinat sistemlerinde olduğu gibi, kutupsal koordinat sisteminde de iki koordinat vardır: r ("radyal koordinat" ya da "ışınsal koordinat") ve θ ("açısal koordinat", "kutupsal açı" ya da "yatay açı"; bazen φ veya t ile gösterilir). r koordinatı, kutuptan olan ışınsal uzaklığı; θ koordinatı ise noktanın üzerinde bulunduğu ışının, bazen "kutupsal eksen" de denilen 0° ışınından saat yönünün tersi yönündeki açısını ifade eder. 0° ışını, Kartezyen koordinat sisteminde "pozitif x ekseni" olarak bilinir.
Örneğin, kutupsal koordinatları (3, 60°) olan bir nokta, kutupsal eksene 60° açı ile duran ışın üzerinde kutuptan 3 birim uzaklıkta bulunur. Koordinatları (-3, 240°) olan nokta da aynı yerde gösterilecektir çünkü bir negatif ışınsal uzaklık, karşıt ışın üzerinde pozitif uzaklık olarak ölçülür (240° − 180° = 60°).
Kutupsal koordinat sisteminin Kartezyen koordinat sisteminde bulunmayan bir önemli özelliği, belli bir noktanın sonsuz sayıda farklı koordinat ile belirtilebilmesidir. Genel olarak, n herhangi bir tam sayı olmak üzere, herhangi bir (r, θ) noktası (r, θ ± n×360°) veya (−r, θ ± (2n + 1)180°) olarak gösterilebilir. Eğer bir noktanın r koordinatı 0 ise, o nokta θ koordinatından bağımsız olarak kutup üzerinde bulunur.
Radyan ölçüsünün kullanımı
Kutupsal sistemde açılar, genel olarak ya derece ya da radyan cinsinden ifade edilir ve bunun için de 2π rad = 360° dönüşümü kullanılır. Seçim çoğunlukla ihtiyaca bağlıdır. Denizcilik uygulamalarında derece ölçüsü kullanılırken, özellikle dönüş mekaniği gibi bazı fizik uygulamalarında ise dairenin çevresinin (c) yarıçapına (r) oranına dayanan radyan ölçüsü kullanılır (c = 2πr).
Kutupsal ve kartezyen koordinatlar arası dönüşüm
Kutupsal koordinatlar r ve θ, kartezyen koordinatlara şu şekilde dönüştürülebilir.
Bu iki formüle göre x ve y cinsinden elde edilen dönüşüm formülleri ise şöyledir:
Eğer x = 0 ve
- y pozitifse, θ = 90° (π/2 rad);
- y negatifse, θ = 270° (3π/2 rad) olur.
Kutupsal denklemler
Kutupsal koordinatlar ile ifade edilmiş bir eğri denklemi "kutupsal denklem" olarak bilinir ve genellikle r, θ'nın bir fonksiyonu olarak yazılır.
Kutupsal denklemler değişik simetri biçimleri gösterebilir. Bir eğri,
- eğer r(−θ) = r(θ) ise 0°/180° yatay ışınına göre,
- eğer r(π−θ) = r(θ) ise 90°/270° dikey ışınına göre ve
- eğer r(θ−α) = r(θ) ise saat yönünün tersinde, rotasyonel (dönel) olarak kutup noktasına göre α° kadar simetrik olacaktır.

Çember
Merkezi (r0, φ) noktasında ve yarıçapı a olan herhangi bir çemberin genel denklemi şu şekildedir:
Bu denklem özel durumlar için çeşitli yollarla basitleştirilebilir. Örneğin
,
merkezi kutup noktasında ve yarıçapı a olan çember için yazılmış denklemdir.
Doğru
Kutuptan geçen ışınsal doğrular şu denklemle gösterilir:
Burada φ, doğrunun eğim açısıdır ve m'nin Kartezyen koordinat sistemindeki eğimi temsil ettiği
denklemi ile de ifade edilebilir.
Kutup noktasından geçmeyen herhangi bir doğru, ışınsal bir doğruya diktir. θ = φ doğrusunu (r0, φ) noktasında dik kesen doğrunun denklemi ise şöyledir:
.

Kutupsal gül
Kutupsal gül, taç yapraklı bir çiçeği andıran ve sadece kutupsal bir denklem ile ifade edilebilen ünlü bir matematiksel eğridir. Şu denklemlerle tanımlanır:
veya
a değişkeninin gülün yapraklarının uzunluğunu ifade ettiği bu denklemlerde eğer k bir tam sayı ise, k tek sayı olduğunda bu denklemler ile k-yapraklı bir gül ve çift sayı olduğundaysa 2k-yapraklı bir gül elde edilir. Eğer k tam sayı değilse, yaprak sayısı da tam sayı olmayacağı için, bir daire şekli oluşur. Dikkat edilmesi gereken nokta, bu denklemlerle 4'ün katlarının 2 fazlası (2, 6, 10, 14, ...) kadar sayıda taç yaprak elde etmenin mümkün olmadığıdır.

Arşimet spirali
Arşimet spirali, Arşimet tarafından keşfedilmiş ve gene yalnızca bir kutupsal denklem ile tanımlanabilen, ünlü bir spiraldir. Şu denklemle ifade edilir:
.
a değişkeninin değişimi spirali döndürürken, b değişkeni spiralin kolları arasındaki daima sabit olan uzaklığı kontrol eder. Arşimet spirali, θ > 0 ve θ < 0 değerleri için iki kola sahiptir. İki kol kutup noktasında birbirine düzgün biçimde bağlanır. Kollardan birinin 90°/270° doğrusu üzerinden ayna simetrisi alınırsa, diğer kol elde edilir.
Konik kesitler

Büyük ekseni kutupsal eksen (0° ışını) üzerinde, bir odağı kutup noktasında ve diğer odağı da kutupsal eksen üzerindeki başka bir noktada bulunan bir konik kesit şu kutupsal denklem ile tanımlanır:
.
Burada e eksantriklik ve l de (semi-latus rectum) büyük eksene dik olarak bir odaktan eğriye kadar ölçülen uzaklıktır. Denklem; e > 1 ise bir hiperbol, e = 1 ise bir parabol ve e < 1 ise bir elips oluşturur. e < 1 koşulunun özel bir durumu olarak e = 0 ise, yarıçapı l olan bir çember elde edilir.
Diğer eğriler
Kutupsal koordinat sisteminin dairesel özelliği, birçok eğrinin Kartezyen biçimdense kutupsal bir denklemle çok daha kolay tanımlanmasını sağlar. Bu eğrilerin arasında , ve özel bir tip limaçon olan kardiyoidler vardır.
Calculus (analiz)
Kutupsal koordinatlar ile ifade edilmiş denklemlere kalkulus (diferansiyel ve integral hesaplamalar) uygulanabilir.
Diferansiyel hesaplama
Bir r(θ) kutupsal eğrisine herhangi bir noktasından teğet olan doğrunun Kartezyen eğimini bulmak için, eğri öncelikle parametrelere bağlı bir denklem sistemi ile tanımlanır:
Sonra, bu denklemlerin θ'ya göre türevlerinin alınmasıyla şu denklemler elde edilir:
Birinci denklemin ikinciyle bölünmesi sonucunda da eğriye (r, r(θ)) noktasında teğet olan doğrunun Kartezyen eğimine ait denklem elde edilir:
İntegral hesaplama
0 < b − a < 2π olmak üzere, r(θ) eğrisinin [a, b] kapalı aralığında kalan kısmının altında kalan alanı bulmak için, öncelikle eğri bir Riemann toplamı olarak tanımlanır.
- İlk olarak, [a, b] aralığı n kadar alt aralığa bölünür (burada n, isteğe bağlı seçilmiş pozitif bir tam sayıdır). Böylece, her alt aralığın uzunluğunu temsil eden Δθ, aralığın tüm uzunluğunun (b − a) alt aralık sayısına (n) bölümüne eşit olur.
- Her i = 1, 2, …, n alt aralığı için θi'nin alt aralığın orta noktası olduğu kabul edilir ve merkezi kutupta, yarıçapı r(θi) ve merkezî açısı Δθ olan birer sektör çizilir.
- Buna göre, çizilmiş her sektörün alanı şu denklemle verilebilir:
- Dolayısıyla, tüm sektörlerin toplam alanı da altta sunulan denklemle tanımlanır:
n alt aralıklarının sayısı ne kadar artarsa, söz konusu alanın ölçümü de gerçek alana o kadar çok yaklaşır. Böylece, [a, b] aralığındaki r(θ) eğrisinin altında kalan alan söyle tanımlanabilir:
Bu ifade, aşağıdaki integralin Riemann toplamıdır:
Vektörel hesaplamalar
Hesaplamalar, denklemlerin kutupsal koordinatlar içinde ifade edilmesi ile bu koordinatlarda uygulanabilir. 

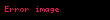
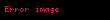



.

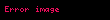


,
ve toplam alan 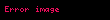
Üç boyut
Kutupsal koordinat sistemi, biri silindrik koordinat sistemi ve diğeri de küresel koordinat sistemi olmak üzere, iki farklı koordinat sistemi ile üç boyuta genişletilir. Her iki sistem de iki boyutlu kutupsal koordinatları bir alt küme olarak kullanır.

Silindirik koordinatlar
Silindirik koordinat sistemi, düzlemden ayrı duran bir noktanın düzleme olan yüksekliğini ölçebilecek üçüncü bir koordinatı iki boyutlu kutupsal koordinat sistemine ekleyerek elde edilir. Bu, kartezyen koordinat sistemini üç boyuta genişletmek için kullanılana benzer bir yöntemdir. İki boyutlu kutupsal koordinat düzlemine dik duran ve kutup noktasından geçen üçüncü koordinat, genellikle h ile gösterilir dikdüzlemine Üçüncü koordinat genelde h ile gösterilir. Buna göre de üç silindirik koordinat, (r, θ, h) yazımı ile ifade edilir.
Silindirik koordinatların Kartezyen koordinatlara dönüşümü şu şekilde olur:

Küresel koordinatlar
Kutupsal koordinatlar, (ρ, φ, θ) koordinatları kullanılarak da üç boyuta genişletilebilir. Burada;
- ρ, kutup noktasından olan uzaklık,
- φ, z ekseninden olan açı ("eş enlem" (colatitude) ya da "zirve" (zenith) de denir; 0'dan 180°'ye kadar ölçülür) ve
- θ da kutupsal koordinatlardaki gibi, x ekseninden olan açıdır.
"Küresel koordinat sistemi" olarak adlandırılan bu sistem, Dünya için kullanılan enlem ve boylam sistemine benzerdir:
- enlem, φ'nin tümleyicisidir ve δ = 90° − φ eşitliğiyle belirlenir;
- boylam da l = θ − 180° ile saptanır.
Küresel koordinat sistemini oluşturan üç koordinatın, Kartezyen sisteme dönüşümü şu şekildedir.
hda
Uygulamalar
Robot bilimi
Hareket edebilen çoğu robot, seyir için kutupsal koordinat sistemini ya da onun biraz değiştirilmiş hâlini kullanır. Bu yapay zekâ için çok uygundur çünkü koordinat sisteminin merkezini (kutbunu) daima robotun o andaki konumu oluşturur. Dolayısıyla, robotun herhangi bir zamanda koordinat sisteminin neresinde olduğunu hesaplamasına gerek yoktur: tek gereken, hangi yönde ve ne kadar uzağa gideceğini belirlemesidir. Eğer robotlar kartezyen koordinat sistemini kullanarak yol alsalardı, hareket için gerekli uzaklık ve açı hesaplamaları için cebir ve trigonometri kullanmak gerekirdi. Oysa, kutupsal koordinat sistemindeki bir açı ile ifade edilen yön ile katedilmesi gereken uzaklık bilgisi, robotun tam istenen yere gitmesini sağlamak için yeterlidir.
Havacılık
Havalanan uçaklar, seyir için kutupsal koordinat sisteminin biraz değiştirilmiş bir çeşidini kullanırlar. Bu sistemde, genellikle "yön 360" (heading 360) olarak adlandırılan 0° ışını dikeydir ve açılar saatin tersi yönde değil, saat yönünde devam eder. Yön 360 manyetik kuzeye denk gelirken, 90, 180 ve 270 yönleri de sırasıyla manyetik doğu, güney ve batıya denk gelir. Dolayısıyla, örneğin doğuya doğru 5 deniz mili kadar yol alacak bir uçak, yön 90 üzerinde 5 birim katedecek demektir.

Arşimet spirali
Arşimet spiralinin gerçek dünyada pek çok uygulaması vardır.
Örneğin, Arşimet spirali şekilli ve birbirinin içine geçmiş aynı büyüklükteki iki sarmal, sıvı ya da gaz gibi akışkanları pompalamak ya da sıkıştırmak için kullanılan temelini oluşturur. Sarmallardan biri sabit dururken, diğeri kendi çevresinde dönmemek üzere merkez dışı (eksantrik) bir dönüş hareketi yapar ve akışkanı iki sarmalın duvarları arasında sıkıştırarak ilerletir.
Gramofon plakların çok erken dönemlerinde, plak üzerindeki oluklar bir Arşimet spirali oluşturacak şekilde açılır ve bu şekilde, olukların birbirlerinden eş uzaklıkta durmaları sağlanarak, bir plağın üstüne en çok miktarda müzik kaydedilmeye çalışılırdı. Ancak sonraları, daha iyi ses kalitesi elde edebilmek için bu uygulamadan vazgeçilmiştir.
Kepler'in gezegensel hareket kanunları

Kutupsal koordinatlar, Kepler'in gezegensel hareket kanunları için doğal bir ifade yöntemi sağlar.
Kepler'in birinci kanununa göre, bir yıldız çevresindeki bir gezegenin yörüngesi, bir odağı sistemin kütle merkezinde oturan bir elipstir. Bu elipsi ifade etmek için, yukarıdaki "Konik kesitler" bölümünde verilmiş olan denklem kullanılabilir.
Kepler'in ikinci kanunu olan "eşit alanlar kanunu" ise şunu söyler: "bir gezegen ile onun yıldızını birleştiren bir doğru, eşit zaman aralıklarında birbirine eşit alanlar tarar"; yani, 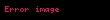
Ayrıca bakınız
Diğer koordinat sistemleri
Kaynakça
- İngilizce Wikipedia 23 Kasım 2006 tarihli Kutupsal koordinat sistemleri maddesi
- ^ Friendly, Michael. . 20 Mart 2011 tarihinde kaynağından arşivlendi.
- ^ "The MacTutor History of Mathematics archive: Coolidge's Origin of Polar Coordinates". 1 Haziran 2006 tarihinde kaynağından . Erişim tarihi: 24 Kasım 2006.
- ^ Coolidge, Julian Lowell (1952). "The Origin of Polar Coordinates". American Mathematical Monthly. Cilt 59. ss. 78-85.
- ^ Daniel Klaasen. Historical Topics for the Mathematical Classroom.
- ^ Miller, Jeff. "Earliest Known Uses of Some of the Words of Mathematics". 19 Temmuz 2008 tarihinde kaynağından .
- ^ Smith, David Eugene (1925). History of Mathematics, Vol II. Ginn and Co.
- ^ Brown, Richard G. (1997). Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis. McDougal Littell Inc. .
- ^ "Polar Coordinates and Graphing" (PDF). 13 Nisan 2006. 15 Şubat 2012 tarihinde kaynağından (PDF) arşivlendi.
- ^ Serway, Raymond A. ve Jewett, Jr., John W. (2005). Principles of Physics. Brooks/Cole—Thomson Learning. .
- ^ a b "Mathworld-Polar Coordinates". 28 Ekim 2006 tarihinde kaynağından . Erişim tarihi: 24 Kasım 2006.
- ^ . 5 Ağustos 2015 tarihinde kaynağından arşivlendi.
- ^ Ward, Robert L. . 4 Ağustos 2015 tarihinde kaynağından arşivlendi.
- ^ Lawrence S. Husch. . 11 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 25 Kasım 2006.
- ^ Lawrence S. Husch. . 2 Temmuz 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 25 Kasım 2006.
- ^ Wattenberg, Frank (1997). . 16 Mayıs 2013 tarihinde kaynağından arşivlendi.
- ^ . 8 Temmuz 2015 tarihinde kaynağından arşivlendi.
- ^ "Air Traffic Control". 12 Temmuz 2007 tarihinde kaynağından .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte kutupsal koordinat sistemi veya polar koordinat sistemi birer aci ve Kartezyen koordinat sistemindeki orijinin esdegeri olup kutup olarak bilinen bir merkez noktaya olan uzakliklar ile tanimlandigi iki boyutlu bir koordinat sistemidir Kutupsal koordinat sistemi matematik fizik muhendislik denizcilik robot teknolojisi gibi bircok alanda kullanilir Bu sistem iki nokta arasindaki iliskinin aci ve uzaklik ile daha kolay ifade edilebildigi durumlar icin ozellikle kullanislidir Kartezyen koordinat sisteminde boyle bir iliski ancak trigonometrik formuller ile bulunabilir Kutupsal denklemler cogu egri tipi icin en kolay bazilari icinse yegane tanimlama yontemidir Cesitli acilarla bolunmus kutupsal bir izgara sistemiTarihceAntik Yunan uygarligi nda aci ve yaricap kavramlarinin kullanildigi bilinmektedir MO 190 120 her aci icin uzunluklarini veren bir kiris fonksiyonlari tablosu olusturulmustur ve yildizlarin konumlarini belirlemek icin kutupsal koordinatlar kullandigina iliskin kaynaklar bulunmaktadir Spiraller Uzerine On Spirals adli eserinde Arsimet unlu spiralini yaricapin aciya bagli oldugu bir fonksiyon olarak tanimlar Bununla beraber Yunan calismalari koordinat sistemini tam olarak tanimlayamamistir Kutupsal koordinatlari resmi bir koordinat sisteminin parcasi olarak ilk olarak kimin tanimladigina iliskin farkli soylemler vardir Konunun tarihcesi Harvard profesoru in Kutupsal Koordinatlarin Kaynagi Origin of Polar Coordinates adli kitabinda anlatilmistir ve Bonaventura Cavalieri yaklasik ayni zamanda birbirinden bagimsiz olarak kavramlari olusturmaya baslamistir Saint Vincent calismalarini 1625 yilinda yazmis ve 1647 yilinda yayinlamisken Cavalieri de 1635 yilinda kendi calismalarinin ilk baskisini yapip 1653 yilinda elden gecirilmis bir surumunu yayinlamistir Bir Arsimet spirali icindeki alanla ilgili bir problemin cozumunde kutupsal koordinat sisteminden ilk yararlanan Cavalieri olmustur Daha sonra Blaise Pascal parabolik yaylarin uzunlugunu hesaplamak icin kutupsal koordinatlari kullanmistir 1671 yilinda yazilmis ve 1736 yilinda basilmis olan calismasiyla Isaac Newton kutupsal koordinatlara bir duzlemdeki herhangi bir noktanin yerini saptama yontemi olarak bakan ilk kisi olmustur Newton kutupsal koordinatlar ve diger dokuz koordinat sistemi arasindaki donusumleri incelemistir Acta eruditorum 1691 adli calismasinda Jacob Bernoulli sirasiyla kutup ve kutupsal eksen olarak adlandirdigi bir nokta ve o noktanin uzerinde yer aldigi eksenden olusan bir sistem kullanmistir Bu sistemde koordinatlar kutba gore uzaklik ve kutup eksenine gore aci ile belirtilmistir Bernoulli nin calismasi bu koordinatlarla tanimlanmis egrilerin egim yaricaplarini hesaplamaya kadar ilerlemistir Gregorio Fontana ya atfedilmis olan kutupsal koordinatlar terimi 18 yuzyil Italyan yazarlari tarafindan kullanilmistir Terimin Ingilizce yayinlarda ilk yer alisi in ya ait Diferansiyel ve Integral Hesaplamalar Differential and Integral Calculus adli kitabini cevirmesi ile 1816 yilinda olmustur Alexis Clairaut ve Leonhard Euler kutupsal koordinat kavraminin uc boyuta uyarlanmasinda rol oynamislardir Kutupsal koordinatlar ile noktalarin belirtilmesi 3 60 ve 4 210 noktalari Tum iki boyutlu koordinat sistemlerinde oldugu gibi kutupsal koordinat sisteminde de iki koordinat vardir r radyal koordinat ya da isinsal koordinat ve 8 acisal koordinat kutupsal aci ya da yatay aci bazen f veya t ile gosterilir r koordinati kutuptan olan isinsal uzakligi 8 koordinati ise noktanin uzerinde bulundugu isinin bazen kutupsal eksen de denilen 0 isinindan saat yonunun tersi yonundeki acisini ifade eder 0 isini Kartezyen koordinat sisteminde pozitif x ekseni olarak bilinir Ornegin kutupsal koordinatlari 3 60 olan bir nokta kutupsal eksene 60 aci ile duran isin uzerinde kutuptan 3 birim uzaklikta bulunur Koordinatlari 3 240 olan nokta da ayni yerde gosterilecektir cunku bir negatif isinsal uzaklik karsit isin uzerinde pozitif uzaklik olarak olculur 240 180 60 Kutupsal koordinat sisteminin Kartezyen koordinat sisteminde bulunmayan bir onemli ozelligi belli bir noktanin sonsuz sayida farkli koordinat ile belirtilebilmesidir Genel olarak n herhangi bir tam sayi olmak uzere herhangi bir r 8 noktasi r 8 n 360 veya r 8 2n 1 180 olarak gosterilebilir Eger bir noktanin r koordinati 0 ise o nokta 8 koordinatindan bagimsiz olarak kutup uzerinde bulunur Radyan olcusunun kullanimi Kutupsal sistemde acilar genel olarak ya derece ya da radyan cinsinden ifade edilir ve bunun icin de 2p rad 360 donusumu kullanilir Secim cogunlukla ihtiyaca baglidir Denizcilik uygulamalarinda derece olcusu kullanilirken ozellikle donus mekanigi gibi bazi fizik uygulamalarinda ise dairenin cevresinin c yaricapina r oranina dayanan radyan olcusu kullanilir c 2pr Kutupsal ve kartezyen koordinatlar arasi donusum Kutupsal koordinatlar r ve 8 kartezyen koordinatlara su sekilde donusturulebilir x rcos 8 displaystyle x r cos theta y rsin 8 displaystyle y r sin theta Bu iki formule gore x ve y cinsinden elde edilen donusum formulleri ise soyledir r x2 y2 displaystyle r sqrt x 2 y 2 8 arctan yxx 0 displaystyle theta arctan frac y x qquad x neq 0 Eger x 0 ve y pozitifse 8 90 p 2 rad y negatifse 8 270 3p 2 rad olur Kutupsal denklemlerKutupsal koordinatlar ile ifade edilmis bir egri denklemi kutupsal denklem olarak bilinir ve genellikle r 8 nin bir fonksiyonu olarak yazilir Kutupsal denklemler degisik simetri bicimleri gosterebilir Bir egri eger r 8 r 8 ise 0 180 yatay isinina gore eger r p 8 r 8 ise 90 270 dikey isinina gore ve eger r 8 a r 8 ise saat yonunun tersinde rotasyonel donel olarak kutup noktasina gore a kadar simetrik olacaktir r 8 1 denklemi ile verilmis cemberCember Merkezi r0 f noktasinda ve yaricapi a olan herhangi bir cemberin genel denklemi su sekildedir r2 2rr0cos 8 f r02 a2 displaystyle r 2 2rr 0 cos theta varphi r 0 2 a 2 Bu denklem ozel durumlar icin cesitli yollarla basitlestirilebilir Ornegin r 8 a displaystyle r theta a merkezi kutup noktasinda ve yaricapi a olan cember icin yazilmis denklemdir Dogru Kutuptan gecen isinsal dogrular su denklemle gosterilir 8 f displaystyle theta varphi Burada f dogrunun egim acisidir ve m nin Kartezyen koordinat sistemindeki egimi temsil ettigi f arctan m displaystyle varphi arctan m denklemi ile de ifade edilebilir Kutup noktasindan gecmeyen herhangi bir dogru isinsal bir dogruya diktir 8 f dogrusunu r0 f noktasinda dik kesen dogrunun denklemi ise soyledir r 8 r0sec 8 f displaystyle r theta r 0 sec theta varphi r 8 2 sin 48 denklemi ile verilmis kutupsal gul sekli Kutupsal gul Kutupsal gul tac yaprakli bir cicegi andiran ve sadece kutupsal bir denklem ile ifade edilebilen unlu bir matematiksel egridir Su denklemlerle tanimlanir r 8 acos k8 displaystyle r theta a cos k theta veya r 8 asin k8 displaystyle r theta a sin k theta a degiskeninin gulun yapraklarinin uzunlugunu ifade ettigi bu denklemlerde eger k bir tam sayi ise k tek sayi oldugunda bu denklemler ile k yaprakli bir gul ve cift sayi oldugundaysa 2k yaprakli bir gul elde edilir Eger k tam sayi degilse yaprak sayisi da tam sayi olmayacagi icin bir daire sekli olusur Dikkat edilmesi gereken nokta bu denklemlerle 4 un katlarinin 2 fazlasi 2 6 10 14 kadar sayida tac yaprak elde etmenin mumkun olmadigidir 0 lt 8 lt 6p icin r 8 8 denklemi ile verilmis Arsimet spiralinin bir kolu Arsimet spirali Arsimet spirali Arsimet tarafindan kesfedilmis ve gene yalnizca bir kutupsal denklem ile tanimlanabilen unlu bir spiraldir Su denklemle ifade edilir r 8 a b8 displaystyle r theta a b theta a degiskeninin degisimi spirali dondururken b degiskeni spiralin kollari arasindaki daima sabit olan uzakligi kontrol eder Arsimet spirali 8 gt 0 ve 8 lt 0 degerleri icin iki kola sahiptir Iki kol kutup noktasinda birbirine duzgun bicimde baglanir Kollardan birinin 90 270 dogrusu uzerinden ayna simetrisi alinirsa diger kol elde edilir Konik kesitler Semi latus rectum mesafesinin gosterildigi bir elips Buyuk ekseni kutupsal eksen 0 isini uzerinde bir odagi kutup noktasinda ve diger odagi da kutupsal eksen uzerindeki baska bir noktada bulunan bir konik kesit su kutupsal denklem ile tanimlanir r l 1 ecos 8 displaystyle r l over 1 e cos theta Burada e eksantriklik ve l de semi latus rectum buyuk eksene dik olarak bir odaktan egriye kadar olculen uzakliktir Denklem e gt 1 ise bir hiperbol e 1 ise bir parabol ve e lt 1 ise bir elips olusturur e lt 1 kosulunun ozel bir durumu olarak e 0 ise yaricapi l olan bir cember elde edilir Diger egriler Kutupsal koordinat sisteminin dairesel ozelligi bircok egrinin Kartezyen bicimdense kutupsal bir denklemle cok daha kolay tanimlanmasini saglar Bu egrilerin arasinda ve ozel bir tip limacon olan kardiyoidler vardir Calculus analiz Kutupsal koordinatlar ile ifade edilmis denklemlere kalkulus diferansiyel ve integral hesaplamalar uygulanabilir Diferansiyel hesaplama Bir r 8 kutupsal egrisine herhangi bir noktasindan teget olan dogrunun Kartezyen egimini bulmak icin egri oncelikle parametrelere bagli bir denklem sistemi ile tanimlanir x r 8 cos 8 displaystyle x r theta cos theta y r 8 sin 8 displaystyle y r theta sin theta Sonra bu denklemlerin 8 ya gore turevlerinin alinmasiyla su denklemler elde edilir dxd8 r 8 cos 8 r 8 sin 8 displaystyle tfrac dx d theta r theta cos theta r theta sin theta dyd8 r 8 sin 8 r 8 cos 8 displaystyle tfrac dy d theta r theta sin theta r theta cos theta Birinci denklemin ikinciyle bolunmesi sonucunda da egriye r r 8 noktasinda teget olan dogrunun Kartezyen egimine ait denklem elde edilir dydx r 8 sin 8 r 8 cos 8 r 8 cos 8 r 8 sin 8 displaystyle frac dy dx frac r theta sin theta r theta cos theta r theta cos theta r theta sin theta Integral hesaplama 0 lt b a lt 2p olmak uzere r 8 egrisinin a b kapali araliginda kalan kisminin altinda kalan alani bulmak icin oncelikle egri bir Riemann toplami olarak tanimlanir Ilk olarak a b araligi n kadar alt araliga bolunur burada n istege bagli secilmis pozitif bir tam sayidir Boylece her alt araligin uzunlugunu temsil eden D8 araligin tum uzunlugunun b a alt aralik sayisina n bolumune esit olur Her i 1 2 n alt araligi icin 8i nin alt araligin orta noktasi oldugu kabul edilir ve merkezi kutupta yaricapi r 8i ve merkezi acisi D8 olan birer sektor cizilir Buna gore cizilmis her sektorun alani su denklemle verilebilir 12r 8i 2D8 displaystyle tfrac 1 2 r theta i 2 Delta theta Dolayisiyla tum sektorlerin toplam alani da altta sunulan denklemle tanimlanir i 1n12r 8i 2D8 displaystyle sum i 1 n tfrac 1 2 r theta i 2 Delta theta n alt araliklarinin sayisi ne kadar artarsa soz konusu alanin olcumu de gercek alana o kadar cok yaklasir Boylece a b araligindaki r 8 egrisinin altinda kalan alan soyle tanimlanabilir limn i 1n12r 8i 2D8 displaystyle lim n to infty sum i 1 n tfrac 1 2 r theta i 2 Delta theta Bu ifade asagidaki integralin Riemann toplamidir 12 abr 8i 2d8 displaystyle frac 1 2 int a b r theta i 2 d theta Vektorel hesaplamalar Hesaplamalar denklemlerin kutupsal koordinatlar icinde ifade edilmesi ile bu koordinatlarda uygulanabilir r displaystyle mathbf r r ve 8 displaystyle theta t zamanina bagli olmak uzere rcos 8 rsin 8 displaystyle r cos theta r sin theta pozisyonundaki vektor olsun r displaystyle hat mathbf r r displaystyle mathbf r yonundeki birim vektor ve 8 displaystyle hat boldsymbol theta r displaystyle mathbf r icin uygun acilardaki birim vektor olsun Konumun birinci ve ikinci turevleri sunlardir drdt r r r8 8 displaystyle frac d mathbf r dt dot r hat mathbf r r dot theta hat boldsymbol theta d2rdt2 r r8 2 r r8 2r 8 8 displaystyle frac d 2 mathbf r dt 2 ddot r r dot theta 2 hat mathbf r r ddot theta 2 dot r dot theta hat boldsymbol theta A displaystyle mathbf A egri uzerindeki bir noktayi odak alarak cizilen cizginin supurdugu alan olarak alindiginda limit icinde dA displaystyle d mathbf A r displaystyle mathbf r ve dr displaystyle d mathbf r tarafindan sekillendirilmis paralelkenar alaninin yarisidir dA 12 r dr displaystyle dA begin matrix frac 1 2 end matrix mathbf r times d mathbf r ve toplam alan dA displaystyle d mathbf A nin zamana gore integralinin alinmasi ile bulunur Uc boyutKutupsal koordinat sistemi biri silindrik koordinat sistemi ve digeri de kuresel koordinat sistemi olmak uzere iki farkli koordinat sistemi ile uc boyuta genisletilir Her iki sistem de iki boyutlu kutupsal koordinatlari bir alt kume olarak kullanir Silindirik koordinatlar ile cizilmis iki noktaSilindirik koordinatlar Silindirik koordinat sistemi duzlemden ayri duran bir noktanin duzleme olan yuksekligini olcebilecek ucuncu bir koordinati iki boyutlu kutupsal koordinat sistemine ekleyerek elde edilir Bu kartezyen koordinat sistemini uc boyuta genisletmek icin kullanilana benzer bir yontemdir Iki boyutlu kutupsal koordinat duzlemine dik duran ve kutup noktasindan gecen ucuncu koordinat genellikle h ile gosterilir dikduzlemine Ucuncu koordinat genelde h ile gosterilir Buna gore de uc silindirik koordinat r 8 h yazimi ile ifade edilir Silindirik koordinatlarin Kartezyen koordinatlara donusumu su sekilde olur x rcos 8 displaystyle x r cos theta y rsin 8 displaystyle y r sin theta z h displaystyle z h Kuresel koordinatlar kullanilarak cizilmis bir noktaKuresel koordinatlar Kutupsal koordinatlar r f 8 koordinatlari kullanilarak da uc boyuta genisletilebilir Burada r kutup noktasindan olan uzaklik f z ekseninden olan aci es enlem colatitude ya da zirve zenith de denir 0 dan 180 ye kadar olculur ve 8 da kutupsal koordinatlardaki gibi x ekseninden olan acidir Kuresel koordinat sistemi olarak adlandirilan bu sistem Dunya icin kullanilan enlem ve boylam sistemine benzerdir enlem f nin tumleyicisidir ve d 90 f esitligiyle belirlenir boylam da l 8 180 ile saptanir Kuresel koordinat sistemini olusturan uc koordinatin Kartezyen sisteme donusumu su sekildedir x rsin ϕcos 8 displaystyle x rho sin phi cos theta y rsin ϕsin 8 displaystyle y rho sin phi sin theta hda z rcos ϕ displaystyle z rho cos phi UygulamalarRobot bilimi Hareket edebilen cogu robot seyir icin kutupsal koordinat sistemini ya da onun biraz degistirilmis halini kullanir Bu yapay zeka icin cok uygundur cunku koordinat sisteminin merkezini kutbunu daima robotun o andaki konumu olusturur Dolayisiyla robotun herhangi bir zamanda koordinat sisteminin neresinde oldugunu hesaplamasina gerek yoktur tek gereken hangi yonde ve ne kadar uzaga gidecegini belirlemesidir Eger robotlar kartezyen koordinat sistemini kullanarak yol alsalardi hareket icin gerekli uzaklik ve aci hesaplamalari icin cebir ve trigonometri kullanmak gerekirdi Oysa kutupsal koordinat sistemindeki bir aci ile ifade edilen yon ile katedilmesi gereken uzaklik bilgisi robotun tam istenen yere gitmesini saglamak icin yeterlidir Havacilik Havalanan ucaklar seyir icin kutupsal koordinat sisteminin biraz degistirilmis bir cesidini kullanirlar Bu sistemde genellikle yon 360 heading 360 olarak adlandirilan 0 isini dikeydir ve acilar saatin tersi yonde degil saat yonunde devam eder Yon 360 manyetik kuzeye denk gelirken 90 180 ve 270 yonleri de sirasiyla manyetik dogu guney ve batiya denk gelir Dolayisiyla ornegin doguya dogru 5 deniz mili kadar yol alacak bir ucak yon 90 uzerinde 5 birim katedecek demektir Temelde iki Arsimet spiralinden olusan calisma ilkesi Arsimet spirali Arsimet spiralinin gercek dunyada pek cok uygulamasi vardir Ornegin Arsimet spirali sekilli ve birbirinin icine gecmis ayni buyuklukteki iki sarmal sivi ya da gaz gibi akiskanlari pompalamak ya da sikistirmak icin kullanilan temelini olusturur Sarmallardan biri sabit dururken digeri kendi cevresinde donmemek uzere merkez disi eksantrik bir donus hareketi yapar ve akiskani iki sarmalin duvarlari arasinda sikistirarak ilerletir Gramofon plaklarin cok erken donemlerinde plak uzerindeki oluklar bir Arsimet spirali olusturacak sekilde acilir ve bu sekilde oluklarin birbirlerinden es uzaklikta durmalari saglanarak bir plagin ustune en cok miktarda muzik kaydedilmeye calisilirdi Ancak sonralari daha iyi ses kalitesi elde edebilmek icin bu uygulamadan vazgecilmistir Kepler in gezegensel hareket kanunlari Kepler in ikinci kanunu Kutupsal koordinatlar Kepler in gezegensel hareket kanunlari icin dogal bir ifade yontemi saglar Kepler in birinci kanununa gore bir yildiz cevresindeki bir gezegenin yorungesi bir odagi sistemin kutle merkezinde oturan bir elipstir Bu elipsi ifade etmek icin yukaridaki Konik kesitler bolumunde verilmis olan denklem kullanilabilir Kepler in ikinci kanunu olan esit alanlar kanunu ise sunu soyler bir gezegen ile onun yildizini birlestiren bir dogru esit zaman araliklarinda birbirine esit alanlar tarar yani dAdt displaystyle d mathbf A over dt sabittir Bu denklemler Newton un hareket kanunlarindan elde edilebilir ve kutupsal koordinatlarin kullanildigi tam bir turetme Kepler in gezegensel hareket yasalari maddesinde sunulmustur Ayrica bakinizDogru matematik DuzlemDiger koordinat sistemleri Koordinat sistemi Kartezyen koordinat sistemi Silindirik koordinat sistemi Ortogonal koordinatlar Paralel koordinatlarKaynakcaIngilizce Wikipedia 23 Kasim 2006 tarihli Kutupsal koordinat sistemleri maddesi Friendly Michael 20 Mart 2011 tarihinde kaynagindan arsivlendi The MacTutor History of Mathematics archive Coolidge s Origin of Polar Coordinates 1 Haziran 2006 tarihinde kaynagindan Erisim tarihi 24 Kasim 2006 Coolidge Julian Lowell 1952 The Origin of Polar Coordinates American Mathematical Monthly Cilt 59 ss 78 85 Daniel Klaasen Historical Topics for the Mathematical Classroom Miller Jeff Earliest Known Uses of Some of the Words of Mathematics 19 Temmuz 2008 tarihinde kaynagindan Smith David Eugene 1925 History of Mathematics Vol II Ginn and Co Brown Richard G 1997 Advanced Mathematics Precalculus with Discrete Mathematics and Data Analysis McDougal Littell Inc ISBN 0 395 77114 5 Polar Coordinates and Graphing PDF 13 Nisan 2006 15 Subat 2012 tarihinde kaynagindan PDF arsivlendi Serway Raymond A ve Jewett Jr John W 2005 Principles of Physics Brooks Cole Thomson Learning ISBN 0 534 49143 X KB1 bakim Birden fazla ad yazar listesi link a b Mathworld Polar Coordinates 28 Ekim 2006 tarihinde kaynagindan Erisim tarihi 24 Kasim 2006 5 Agustos 2015 tarihinde kaynagindan arsivlendi Ward Robert L 4 Agustos 2015 tarihinde kaynagindan arsivlendi Lawrence S Husch 11 Ekim 2014 tarihinde kaynagindan arsivlendi Erisim tarihi 25 Kasim 2006 Lawrence S Husch 2 Temmuz 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 25 Kasim 2006 Wattenberg Frank 1997 16 Mayis 2013 tarihinde kaynagindan arsivlendi 8 Temmuz 2015 tarihinde kaynagindan arsivlendi Air Traffic Control 12 Temmuz 2007 tarihinde kaynagindan
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State