Matematik ve istatistik bilim dallarında genelleştirilmiş f-ortalaması merkezsel konum ölçülerinden olan değişik ortalamalar için tek bir genel fonksiyon ve formül bulma ve kullanma çabaları sonucu ortaya çıkarılmıştır. Benzer çabalar biraz değişik diğer bir genelleştirilmiş ortalama formülünü vermiştir. Bu nedenle isim karışıklığını önlemek için f-ortalaması çeşitli diğer isimlerde de anılmaktadır. Bazen yarı-aritmetik ortalama adı kullanılmaktadır. Bu kavramı ve formülü ilk geliştiren Rus matematikçisi adına atfen de bazen Kolmogorov ortalaması olarak isimlendirilmektedir.
Tanımlama
Eğer f, reel doğrunun altseti olan 


,
olur ve f-ortalaması
ifadesi ile verilir.
Ters fonksiyon olan 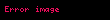
ifadesinin 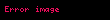

Özellikler
- : f-ortalama hesaplanırken, veriler birbirine eşit alt-bloklara bölüntülenebilip genel sonuca etki yapmadan hesaplar ayrı ayrı alt-bloklara uygulanabilir:
- Elemanların çarpma özelliği korunursa, genel f-ortalamayı etkilemeden her altset için ayrı ortalama önceden hesaplanabilir.
ile şu ifade gerçek olabilir
- Genelleştirilmiş f-ortalamasi
de kaymalar ve yeniden ölçeklenmelerden etkilenmez; yani
.
- Eğer
ise, o halde
de monotoniktir.
İlişkiler
- Eğer
reel doğruya (yahut
nin sıfır olmadığı herhangi bir doğrusal fonksiyon
a) tasarımlanırsa ve
, ise f-ortalaması aritmetik ortalama olur.
- Eğer
pozitif reel sayılar setine tasarımlanırsa ve
, ise f-ortalaması geometrik ortalama olur. f-ortalaması özelliklere uygun olarak bu sonuç eğer pozitif ise ve 1 değilse, dayandığı logaritma bazının ne olduğunun hiç önemi bulunmamaktadır.
- Eğer
pozitif reel sayılar setine tasarımlanırsa ve
, ise f-ortalaması harmonik ortalama olur.
- Eğer
pozitif reel sayılar setine tasarımlanırsa ve
, ise f-ortalaması
üslü olur.
Homojenlik
Ortalama için kullançılan fonksiyonlar ok kere homojendirler. Ancak f-ortalaması için 

sağlanabilir. Ancak bu değişme bazı f-ortalamaları için ve özelliklerin ortadan kaldırabilir.
İçsel kaynaklar
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematik ve istatistik bilim dallarinda genellestirilmis f ortalamasi merkezsel konum olculerinden olan degisik ortalamalar icin tek bir genel fonksiyon ve formul bulma ve kullanma cabalari sonucu ortaya cikarilmistir Benzer cabalar biraz degisik diger bir genellestirilmis ortalama formulunu vermistir Bu nedenle isim karisikligini onlemek icin f ortalamasi cesitli diger isimlerde de anilmaktadir Bazen yari aritmetik ortalama adi kullanilmaktadir Bu kavrami ve formulu ilk gelistiren Rus matematikcisi adina atfen de bazen Kolmogorov ortalamasi olarak isimlendirilmektedir TanimlamaEger f reel dogrunun altseti olan S displaystyle S yi reel sayilara tasarimlayan bir fonksiyon ise ve hem surekli hem de ise o halde su iki sayi olan x1 x2 S displaystyle x 1 x 2 subset S icin f ortalamasi soyle tanimlanir Mf x1 x2 f 1 f x1 f x2 2 displaystyle M f x 1 x 2 f 1 left frac f x 1 f x 2 2 right n displaystyle n buyuklukteki bir veri dizisi x1 xn S displaystyle x 1 dots x n subset S olur ve f ortalamasi Mfx f 1 f x1 f xn n displaystyle M f x f 1 left frac f x 1 cdots f x n n right ifadesi ile verilir Ters fonksiyon olan f 1 displaystyle f 1 mevcut olmasi icin fnin enjektif olmasi gerekir Fonksiyonun surekli olmasi icin f x1 f x2 2 displaystyle frac f left x 1 right f left x 2 right 2 ifadesinin f 1 displaystyle f 1 sahasinda bulunmalidir Boylece enjektif ve surekli olmasi saglanan f kesinlikle olur ve bunun icin x displaystyle x icinde ne bu grubun icindeki en buyuk sayidan daha buyuk ne de grubun en kucuk sayisindan daha kucuk olabilir Ozellikler f ortalama hesaplanirken veriler birbirine esit alt bloklara boluntulenebilip genel sonuca etki yapmadan hesaplar ayri ayri alt bloklara uygulanabilir Mf x1 xn k Mf Mf x1 xk Mf xk 1 x2 k Mf x n 1 k 1 xn k displaystyle M f x 1 dots x n cdot k M f M f x 1 dots x k M f x k 1 dots x 2 cdot k dots M f x n 1 cdot k 1 dots x n cdot k Elemanlarin carpma ozelligi korunursa genel f ortalamayi etkilemeden her altset icin ayri ortalama onceden hesaplanabilir m Mf x1 xk displaystyle m M f x 1 dots x k ile su ifade gercek olabilir Mf x1 xk xk 1 xn Mf m m k tane xk 1 xn displaystyle M f x 1 dots x k x k 1 dots x n M f underbrace m dots m k mbox tane x k 1 dots x n Genellestirilmis f ortalamasi f displaystyle f de kaymalar ve yeniden olceklenmelerden etkilenmez yani a b 0 t g t a b f t x Mfx Mgx displaystyle forall a forall b neq 0 forall t g t a b cdot f t Rightarrow forall x M f x M g x Eger f displaystyle f ise o halde Mf displaystyle M f de monotoniktir IliskilerEger S displaystyle S reel dogruya yahut a displaystyle a nin sifir olmadigi herhangi bir dogrusal fonksiyon x a x b displaystyle x mapsto a cdot x b a tasarimlanirsa ve f id displaystyle f mathrm id ise f ortalamasi aritmetik ortalama olur Eger S displaystyle S pozitif reel sayilar setine tasarimlanirsa ve f ln x displaystyle f ln x ise f ortalamasi geometrik ortalama olur f ortalamasi ozelliklere uygun olarak bu sonuc eger pozitif ise ve 1 degilse dayandigi logaritma bazinin ne oldugunun hic onemi bulunmamaktadir Eger S displaystyle S pozitif reel sayilar setine tasarimlanirsa ve f 1x displaystyle f frac 1 x ise f ortalamasi harmonik ortalama olur Eger S displaystyle S pozitif reel sayilar setine tasarimlanirsa ve f xp displaystyle f x p ise f ortalamasi p displaystyle p uslu olur HomojenlikOrtalama icin kullancilan fonksiyonlar ok kere homojendirler Ancak f ortalamasi icin f displaystyle f fonksiyonlarinin cogu homojen degildir Homojenlik ozelligi girdi veri degerlerini ozel bir homojen ortalama C displaystyle C ile normalize ederek yani Mf Cx Cx f 1 f x1Cx f xnCx n displaystyle M f C x Cx cdot f 1 left frac f left frac x 1 Cx right dots f left frac x n Cx right n right saglanabilir Ancak bu degisme bazi f ortalamalari icin ve ozelliklerin ortadan kaldirabilir Icsel kaynaklarOrtalama Genellestirilmis ortalamaKaynakca Bibby J 1974 Axiomatisations of the average and a further generalisation of monotonic sequences Glasgow Mathematical Journal C 15 say 63 65 Kolmogorov A 1930 Mathematics and mechanics Moskova say 136 138 Rusca
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans
















