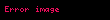Matematikte bir çizgi integrali (bazen yol integrali, eğri integrali veya eğrisel integral de denilir), integrali alınan fonksiyonun bir eğri boyunca değerlendirildiği integraldir. Çeşitli farklı çizgi integralleri kullanılmaktadır. Kapalı eğrinin kullanıldığı durumlarda integrale kontür integrali denildiği de olmaktadır.
İntegrali alınan fonksiyon (integrand), skaler alan veya vektör alanı olabilir. Çizgi integralinin değeri, alanın eğri üzerinde bir skaler fonksiyonla ağırlıklaştırılmış (genelde bu ağırlık yay uzunluğudur veya bir vektör alanı için, vektör alanının bir eğriyle ) olarak aldığı tüm değerlerin toplamının değeridir. Bu ağırlık, çizgi integralini üzerinde tanımlanan daha basit integrallerden ayırır. Fizikteki çoğu basit formül (mesela, ), çizgi integrali bağlamında doğal sürekli analoglara sahiptir (). Çizgi integrali yandaki resimdeki gibi, bir elektrik veya yerçekimsel alanda hareket eden bir nesnenin üzerinde yapılan işi bulur.


Vektör hesabı
Niteliksel bağlamda, çizgi integrali bir eğri boyunca verilmiş olan bir alanın toplam etkisinin ölçümü olarak düşünülebilir.
Bir skaler alanın çizgi integrali
Bir f : U ⊆ Rn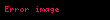
şeklinde tanımlanır. Burada r: [a, b] 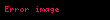
f fonksiyonu integrand, C eğrisi integralin tanım kümesi ve ds sembolü ise . Skaler alanların çizgi integralleri seçilmiş r parametrizasyonuna bağlı değildir.
Bir vektör alanının çizgi integrali
Bir F : U ⊆ Rn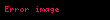
şeklinde tanımlanır. Burada 
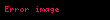
Bir skaler alanın çizgi integrali bu yüzden vektörlerin doğruya her zaman teğet olduğu bir vektör alanının çizgi integralidir.
Vektör alanlarının çizgi integralleri, mutlak değer içindeki r parametrizasyonuna bağlı değildir; ancak eğrinin yönüne bağlıdır. Dha ayrıntılı bir şekilde, parametrizasyonun yönündeki tersi bir değişim çizgi integralinin işaretini değiştirir.
Yol bağımsızlığı
Bir F vektör alanı, bir G skaler alanının gradyanıysa; yani
ise, o zaman G ve r(t) 'nin bileşkesinin türevi
olur ki bu da F 'nin r(t) üzerindeki çizgi integralinin integrandıdır. O zaman, verilen bir C yolu için
olmaktadır. Yazıyla ifade edilirse, F 'nin C üzerindeki integrali sadece G nin r(b) ve r(a) noktalarındaki değerlerine bağlıdır ve bu yüzden aradaki yoldan bağımsızdır.
Bu sebeple, bir skaler alanın gradyanı olan bir vektör alanının çizgi integrali yoldan bağımsız olarak adlandırılır.
Uygulamalar
Çizgi integralinin fizikte birçok uygulaması vardır. Mesela, bir F vektör alanı olarak temsil edilen bir kuvvet alanı içinde yer alan bir C eğrisi üzerinde hareket etmekte olan bir parçacığın üzerinde yapılan iş F 'nin C üzerindeki çizgi integralidir.
Karmaşık çizgi integrali
Çizgi integrali karmaşık analizde temel bir araçtır. U, C'nin açık bir kümesi olsun, 
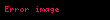
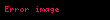
çizgi integrali, [a, b] aralığını a = t0 < t1 < ... < tn = b olacak şekilde daha küçük aralıklara ayırılarak ve
ifadesi göz önüne alınarak düşünülebilir. O zaman, alt aralıkların uzunlukları sıfıra gittikçe, integral bu toplamın limiti olur.
Eğer 

gösterimi, f 'nin 
Karmaşık fonksiyonların çizgi integralleri çeşitli teknikler kullanılarak değerlendirilebilir: İntegral, gerçel ve karmaşık kısımlarına bölünüp problem iki tane gerçel integralin bulunması problemine düşürülebilir, Cauchy integral formülü diğer durumlarda kullanılabilir. Eğer çizgi integralinin alındığı eğri, fonksiyonun analitik olduğu ve içermediği bir bölgede kapalı bir eğriyse, o zaman integralin değeri sadece 0 olur ki bu da Cauchy integral teoremi'nin bir sonucudur. Kalıntı teoremi sebebiyle, gerçel değişkene sahip gerçel değerli fonksiyonların integralini bulmak için çoğu zaman karmaşık düzlemde kontür integralleri kullanılır. (örnek için kalıntı teoremine bakınız.)
Örnek
f(z)=1/z fonksiyonunu ele alalım. C kontürü, eit, 
ifadesini buluruz. Burada, herhangi bir karmaşık z sayısının r, z 'nin modülüsü (mutlak değeri) olacak şekilde reit olarak yazılabileceğini kullandık. Birim çember üzerinde r = 1 olduğu için geriye kalan tek değişken t ile gösterilen açı değişkenidir. Cevap, aynı zamanda Cauchy integral formülü ile de doğrulanabilir.
Bir vektör alanının integrali ile karmaşık çizgi integrali arasındaki ilişki
Karmaşık sayıları 2 boyutlu vektörler olarak alırsak, 2 boyutlu bir vektör alanının çizgi integrali, karşılık gelen karmaşık değerli karmaşık fonksiyonun eşleniğinin çizgi integralinin gerçel kısmına denk gelir. Daha ayrıntılı bir şekilde, 
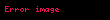

eşitliği elde edilir.
Cauchy-Riemann denklemleri sebebiyle, bir holomorf fonksiyonun eşleniğine karşılık gelen bir vektör alanının sıfırdır. Bu da her iki tip integralin de sıfır olduğu Stokes teoremi ile ilişkilidir.
Ayrıca, çizgi integrali değişken değiştirme kullanılarak da değerlendirilebilir.
Ayrıca bakınız
Dış bağlantılar
- PlanetMath'de yol integrali6 Temmuz 2008 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte bir cizgi integrali bazen yol integrali egri integrali veya egrisel integral de denilir integrali alinan fonksiyonun bir egri boyunca degerlendirildigi integraldir Cesitli farkli cizgi integralleri kullanilmaktadir Kapali egrinin kullanildigi durumlarda integrale kontur integrali denildigi de olmaktadir Integrali alinan fonksiyon integrand skaler alan veya vektor alani olabilir Cizgi integralinin degeri alanin egri uzerinde bir skaler fonksiyonla agirliklastirilmis genelde bu agirlik yay uzunlugudur veya bir vektor alani icin vektor alaninin bir egriyle olarak aldigi tum degerlerin toplaminin degeridir Bu agirlik cizgi integralini uzerinde tanimlanan daha basit integrallerden ayirir Fizikteki cogu basit formul mesela W F s displaystyle W vec F cdot vec s cizgi integrali baglaminda dogal surekli analoglara sahiptir W CF ds displaystyle W int C vec F cdot d vec s Cizgi integrali yandaki resimdeki gibi bir elektrik veya yercekimsel alanda hareket eden bir nesnenin uzerinde yapilan isi bulur Vektor hesabiNiteliksel baglamda cizgi integrali bir egri boyunca verilmis olan bir alanin toplam etkisinin olcumu olarak dusunulebilir Bir skaler alanin cizgi integrali Bir f U Rn displaystyle to R skaler alani icin bir C U boyuncaki cizgi integrali Cfds abf r t r t dt displaystyle int C f ds int a b f mathbf r t mathbf r t dt seklinde tanimlanir Burada r a b displaystyle to C ise r a ve r b C nin son noktalari olacak sekilde C nin herhangi bir birebir orten parametrizasyonudur f fonksiyonu integrand C egrisi integralin tanim kumesi ve ds sembolu ise Skaler alanlarin cizgi integralleri secilmis r parametrizasyonuna bagli degildir Bir vektor alaninin cizgi integrali Bir F U Rn displaystyle to Rn vektor alani icin C U boyunca r yonundeki cizgi integrali CF r dr abF r t r t dt displaystyle int C mathbf F mathbf r cdot d mathbf r int a b mathbf F mathbf r t cdot mathbf r t dt seklinde tanimlanir Burada displaystyle cdot nokta carpimdir ve r a b displaystyle to C ise r a ve r b C nin sonnoktalari olacak sekilde C egrisinin birebir orten bir parametrizasyonudur Bir skaler alanin cizgi integrali bu yuzden vektorlerin dogruya her zaman teget oldugu bir vektor alaninin cizgi integralidir Vektor alanlarinin cizgi integralleri mutlak deger icindeki r parametrizasyonuna bagli degildir ancak egrinin yonune baglidir Dha ayrintili bir sekilde parametrizasyonun yonundeki tersi bir degisim cizgi integralinin isaretini degistirir Yol bagimsizligi Bir F vektor alani bir G skaler alaninin gradyaniysa yani G F displaystyle nabla G mathbf F ise o zaman G ve r t nin bileskesinin turevi dG r t dt G r t r t F r t r t displaystyle frac dG mathbf r t dt nabla G mathbf r t cdot mathbf r t mathbf F mathbf r t cdot mathbf r t olur ki bu da F nin r t uzerindeki cizgi integralinin integrandidir O zaman verilen bir C yolu icin CF r dr abF r t r t dt abdG r t dtdt G r b G r a displaystyle int C mathbf F mathbf r cdot d mathbf r int a b mathbf F mathbf r t cdot mathbf r t dt int a b frac dG mathbf r t dt dt G mathbf r b G mathbf r a olmaktadir Yaziyla ifade edilirse F nin C uzerindeki integrali sadece G nin r b ve r a noktalarindaki degerlerine baglidir ve bu yuzden aradaki yoldan bagimsizdir Bu sebeple bir skaler alanin gradyani olan bir vektor alaninin cizgi integrali yoldan bagimsiz olarak adlandirilir Uygulamalar Cizgi integralinin fizikte bircok uygulamasi vardir Mesela bir F vektor alani olarak temsil edilen bir kuvvet alani icinde yer alan bir C egrisi uzerinde hareket etmekte olan bir parcacigin uzerinde yapilan is F nin C uzerindeki cizgi integralidir Karmasik cizgi integraliCizgi integrali karmasik analizde temel bir aractir U C nin acik bir kumesi olsun g displaystyle gamma a b displaystyle to U ve f U displaystyle to C bir fonksiyon olsun O zaman gf z dz displaystyle int gamma f z dz cizgi integrali a b araligini a t0 lt t1 lt lt tn b olacak sekilde daha kucuk araliklara ayirilarak ve 1 k nf g tk g tk g tk 1 displaystyle sum 1 leq k leq n f gamma t k gamma t k gamma t k 1 ifadesi goz onune alinarak dusunulebilir O zaman alt araliklarin uzunluklari sifira gittikce integral bu toplamin limiti olur Eger g displaystyle gamma surekli turevlenebilir bir egriyse cizgi integrali gercel degiskenli bir fonksiyonun integrali olarak degerlendirilebilir gf z dz abf g t g t dt displaystyle int gamma f z dz int a b f gamma t gamma t dt g displaystyle gamma kapali bir egri oldugu zaman yani baslangic ve bitis noktalari ayniysa gf z dz displaystyle oint gamma f z dz gosterimi f nin g displaystyle gamma boyuncaki cizgi integrali icin kullanilir Karmasik fonksiyonlarin cizgi integralleri cesitli teknikler kullanilarak degerlendirilebilir Integral gercel ve karmasik kisimlarina bolunup problem iki tane gercel integralin bulunmasi problemine dusurulebilir Cauchy integral formulu diger durumlarda kullanilabilir Eger cizgi integralinin alindigi egri fonksiyonun analitik oldugu ve icermedigi bir bolgede kapali bir egriyse o zaman integralin degeri sadece 0 olur ki bu da Cauchy integral teoremi nin bir sonucudur Kalinti teoremi sebebiyle gercel degiskene sahip gercel degerli fonksiyonlarin integralini bulmak icin cogu zaman karmasik duzlemde kontur integralleri kullanilir ornek icin kalinti teoremine bakiniz Ornek f z 1 z fonksiyonunu ele alalim C konturu eit t 0 2p displaystyle t in 0 2 pi seklinde parametrize edilebilen 0 etrafindaki birim cember olsun Degisken degistirmeyle Cf z dz 02p1eitieitdt i 02pe iteitdt displaystyle oint C f z dz int 0 2 pi 1 over e it ie it dt i int 0 2 pi e it e it dt i 02pdt i 2p 0 2pi displaystyle i int 0 2 pi dt i 2 pi 0 2 pi i ifadesini buluruz Burada herhangi bir karmasik z sayisinin r z nin modulusu mutlak degeri olacak sekilde reit olarak yazilabilecegini kullandik Birim cember uzerinde r 1 oldugu icin geriye kalan tek degisken t ile gosterilen aci degiskenidir Cevap ayni zamanda Cauchy integral formulu ile de dogrulanabilir Bir vektor alaninin integrali ile karmasik cizgi integrali arasindaki iliski Karmasik sayilari 2 boyutlu vektorler olarak alirsak 2 boyutlu bir vektor alaninin cizgi integrali karsilik gelen karmasik degerli karmasik fonksiyonun esleniginin cizgi integralinin gercel kismina denk gelir Daha ayrintili bir sekilde r t x t i y t j displaystyle mathbf r t x t mathbf i y t mathbf j ve f z u z iv z displaystyle f z u z iv z ise o zaman sag taraftaki her iki integral de var oldugu ve C nin z t displaystyle z t parametrizasyonu r t displaystyle mathbf r t ile ayni yonde oldugu surece Cf z dz C u iv dz C ui vj dr i C ui vj dr displaystyle int C overline f z dz int C u iv dz int C u mathbf i v mathbf j cdot d mathbf r i int C u mathbf i v mathbf j cdot d mathbf r esitligi elde edilir Cauchy Riemann denklemleri sebebiyle bir holomorf fonksiyonun eslenigine karsilik gelen bir vektor alaninin sifirdir Bu da her iki tip integralin de sifir oldugu Stokes teoremi ile iliskilidir Ayrica cizgi integrali degisken degistirme kullanilarak da degerlendirilebilir Ayrica bakinizDiverjans teoremi Green teoremi Stokes teoremi Yuzey integrali Hacim integraliDis baglantilarPlanetMath de yol integrali6 Temmuz 2008 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans