Bu maddedeki bilgilerin için ek kaynaklar gerekli. (Mart 2020) () |
Kuantum renk dinamiği veya kuantum kromodinamiği (KRD veya KKD), teorik fizikte kuantum kromodinamiği, kuarklar ve gluonlar arasındaki güçlü etkileşimin proton, nötron ve pion gibi kompozit hadronları oluşturan, temel parçacıkların teorisidir.
Aynı zamanda güçlü etkileşim renkyüklü fermiyonlar olan kuarkların SU(3) grubundaki (takımındaki) Yang-Mills kuramı ile de tanımlanabilir. KRD değişme özelliği olmayan ayar kuramı ile gösterilen özel bir kuantum alanlar kuramıdır. Aynı zamanda KRD parçacık fiziğinin standart modelinin önemli bir parçasıdır. Yıllar boyunca oldukça büyük bir miktarda KRD'yi olumlayan deneysel veri toplanmıştır.
KRD kendine has iki özelliğe sahiptir:
- Renkhapsi denilen birinci özellik kuarkların birbirinden ayrıldıkça onları bir arada tutan kuvvetin yokolmamasıdır. Bu özellikten dolayı iki kuarkı birbirinden ayırmak sonsuz enerjiyi gerektirir. Kuarklar hadronların içinde toplu bulunurlar ve yalnız başına gözlemlenmemiştir. Serbest kuark araştırmalarının başarısızlıkla sonuçlanması, KRD'nin matametiksel analizi ile ispatlanmamasına rağmen renkhapsinin fizikçiler tarafından kabul edilen bir düşünce olmasına yol açmıştır. Diğer taraftan renkhapsi olayı örgü KRD'de (lattice QCD) gösterilebilmektedir.
- Asimtotik özgürlük denilin ikinci özellik çok yüksek enerjili tepkimelerde kuarkların ve gluonların çok zayıf etkileşmesidir. KRD'nin bu tahmini 1970'lerde David Politzer, Frank Wilczek ve David Gross tarafından keşfedilmiştir. Bu çalışmaları bahsedilen biliminsanlarına 2004 Nobel fizik ödülünü kazandırmıştır.
Göreceli olarak düşük enerjilerde renkhapsi baskın özelliktir ve yüksek enerjilere çıkıldıkça da asimtotik özgürlük baskın özelliktir. Ama bu iki durumu ayıran geçiş henüz anlaşılmamıştır.
Etimoloji
Kuark terimi 1929'da Murray Gell-Mann tarafından uydurulmuştur. Kuark kelimesinin temeli ise James Joyce'un Finnegans Wake isimli kitabındaki Muster Mark için üç kuark ifadesidir.
KRD'nin üç yükü renkyükü olarak adlandırılır ve insanların görebildiği üç renk olan kırmızı, mavi ve yeşil ile isimlendirilir. İnsanların gördüğü renklerle KRD'nin renkyükleri arasında önemli bir benzerlik yoktur.
Tarihsel gelişim
Kabarcık odası (bubble chamber) ve kıvılcım odasının (spark chamber) 1950'lerde icat edilmesi ile birlikte deneysel olarak parçacık fiziğinde birçok hadron olarak isimlendirilen parçacık bulunmuştur. Gözlemlenen parçacık sayısının çokluğu hadronların tamamının temel parçacık olamayacağı düşüncesini doğurmuştur. Öncelikle Eugene Wigner ve Werner Heisenberg tarafından parçacıklar yük ve izospin düşünülerek sınıflandırılmıştır. Sonra, 1953'te, acayiplik (strangeness) özelliğine göre Murray Gell-Mann ve Kazuhiko Nishijima tarafından sınıflandırılmıştır. Sezgisel algıyı arttırmak için hadronlar benzer özelliklerine ve kütlelerine göre sekiz katlı olarak 1961'de Gell-Mann ve Yuval Ne'eman tarafından sınıflandırılmıştır. Gell-Mann ve George Zweig Shoichi Skata'nın yaklaşımını düzelterek 1963'te bu sınıflandırmaların yapısının üç farklı çeşni ile tanımlanabilecek hadronlardan daha küçük olan kuarklarla açıklanabildiğini göstermişlerdir.
Kuarkların farklı bir kuantum sayısına daha sahip olabileceklerine dair ilk düşünce Boris Struminsky'nin üç acayip (strange) kuarktan oluşan 
Three identical quarks cannot form an antisymmetric S-state. In order to realize an antisymmetric orbital S-state, it is necessary for the quark to have an additional quantum number.
(Üç aynı kuark antisimmetrik S-durumunu oluşturamazlar. Bu antisimmetrik S-durumunun oluşturulabilmesi için kuarkların farklı bir kuantum sayısına sahip olması lazım.)
— B. V. Struminsky, Magnetic moments of barions in the quark model, JINR-Preprint P-1939, Dubna, Submitted on January 7, 1965
Nikolay Bogolgov doktora öğrencisi olan Boris Struminsky'ye bahsedilen araştırmayı yapmayı önermişti. 1965'te Nikolay Bogolyubov, Boris Struminsky ve Albert Tavchelidze kuarkların bahsedilen kuantum serbestlik dereceleri üzerine yeni bir önyayın yaptılar. Bu çalışma Tavchelidze tarafından diğer çalıma arkadaşlarının iznini almadan Mayıs 1965'te Trieste'de (İtalya) düzenlenen uluslararası bir konferansta sunulmuştur.
Serbest kuark araştırmaları sürekli olarak başarısızlıkla sonuçlandığı için ve o zamana kadar temel parçacık serbest bir şekilde gözlemlenebilir ve yalıtılabilir şeklinde tanımlandığından dolayı Gell-Mann sıklıkla kuarkların cebirsel yapılar tanımına da gerçek parçacıklar sınıfına da uygun olmadığını söylemiştir. Gell-Mann'ın söylediği "kuarklar hapsolmuştur fakat güçlü etkileşim de kuantum alanlar kuramı şeklinde tam olarak ifade edilmeyebilir" cümlesiyle de anlatılabilir. Kuarkların hadronlar içinde hapsolması onları o zamanın temel parçacık tanımına dahil edilememesi ve güçlü etkileşimin tam olarak cebirsel bir kuramla anlaşılamaması durumu Gell-Mann'a bunları söyletmiştir.
Richard Feynman yüksek enerji deneylerinin kuarkların gerçek parçacıklar olduğunu gösterdiğini söylemiştir ve kuarkları partonlar şeklinde isimlendirmiştir. (Kuarklar hadronların parçaları olduğu için bu şekilde isimlendirme yapmıştır.) Feynman'ın parçacık tanımına göre temel parçacıklar bir yolu takip edebilen parçacıklardır.
Feynman'ın ve Gell-Mann'ın yaklaşımları arasındaki fark kuramsal fizikçiler arasında derin bir ayrımla sonuçlanmıştır. Feynman kuarkların kuantum mekaniğindeki diğer parçacıklar gibi momentum ve konum dağılımına sahip olduğunu düşünmüştür ve (doğru bir şekilde) parton momentumunun yayılmasının kırınımsal saçılma ile açıklanabileceğine inanmıştır. Diğer taraftan Gell-Mann belirli kuark yüklerinin yerinin belirlenebileceğine inanmış ve kuarkların yerinin uzay zaman kırılmasından dolayı yerlerinin belirlenemeyeceği olasılığına da uzak kalmamıştır. Bu düşünce S-dizey kuramından daha aşırı bir yaklaşımdır.
James Bjorken noktasal parçacık şeklindeki partonların elektronların protonlarla yaptıkları esnek olmayan çarpışmalarında etkisini göstereceğini söylemiştir ve bu tartışmalı bir şekilde 1969'da SLAC deneylerinde doğrulanmıştır. Bu sonuç fizikçilerin güçlü etkileşim için S-dizeyi yaklaşımını bırakmalarıyla sonuçlanmıştır.
David Gross, David Politzer ve Frank Wilczek tarafından güçlü etkileşmede keşfi birçok yüksek enerji deneyinde kuantum alanlar kuramının tedirgileme kuramı (perturbasyon kuramı) tekniğini kullanarak çok hassas öngörüler yapmasına olanak sağlamıştır. Gluonlara dair delil 1979'da PETRA'daki gözlemlenmiştir. Bu deneyler gittikçe hassaslaşmıştır ve şu anki(2011) en hassas haline 'nin (perturbative QCD) doğrulanmasında yüzde birkaçlık oranla CERN'in LEP kısmında ulaşmıştır.
Asimtotik özgürlüğün diğer tarafında renkhapsi bulunmaktadır. Renkyükleri arasındaki kuvvet uzaklıkla düşmediği için kuarkların ve gluonların hadronlardan ayrıştırılamayacağına inanılmaktadır. Kuramın bu yönü örgü KRD hesaplamaları ile doğrulanmıştır. Ama bu doğrulama cebirsel olarak yapılamamıştır. Clay matematik enstitüsü tarafından duyurulan Milenyum ödüllü sorunlardan biri de bu doğrulamadır. Tedirgemeli olmayan (non-perturbative) KRD'nin diğer çalışılan konuları kuark-gluon plazmanın da dahil olduğu kuark maddesinin halleridir.
Kuram
Tanımlamalar
Parçacık fiziğindeki her alan kuramı gözlemlerden çıkarılmış olan doğanın bazı korunum yasaları (simetrileri) üzerine kurulmuştur. Bunlar iki sınıfa ayrılabilir:
- Yerel korunum yasaları; uzay-zamanın her bir noktasında diğer noktalardan bağımsız olarak korunan yasalardır. Bu türdeki korunum yasaları ayar kuramının temelidir ve kendine has ayar bozonlarının kullanılmasını gerektirir.
- Genel korunum yasaları; bu türdeki korunum yasalarının geçerliliğinin uzay-zamanın her noktasında aynı anda olabilmesi gereklidir. Kısaca A noktasındaki korunum başka bir B noktasında da aynı anda sağlanmalıdır.
KRD SU(3) ayar takımında bir ayar kuramıdır ve bu renkyükünün bir yerel korunum yasası oluşturmasıyla elde edilmiştir.
Güçlü etkileşim farklı kuark çeşnileri arasında ayrım gözetmediği için KRD sadece kütle farklarından dolayı korunmayan başka bir deyişle tam korunumu sağlanmayan bir korunum yasasına sahiptir. Enerjinin durumuna göre bazı kuark çeşnilerinin etkileşimlerde aldıkları rol daha fazladır ve bu fark KRD'de tamamıyla çeşniler arasında bahsedilen ve tamamıyla geçerli olmayan korunum yasasının oluşmasıyla sonuçlanır.
Bunlara ek olarak başka genel korunum yasaları da vardır. Bunları tanımlayabilmemiz için sağ-elli ve sol-elli parçacıklar arasında ayrım yapabilmemiz gerekmektedir. Bunu tanımlamak için de ayna örtüşmezliği (chirality) kullanılır. Eğer parçacığın spini hareket yönüne pozitif izdüşüm sağlıyorsa sol-elli, negatif izdüşüm sağlıyorsa da sağ-elli olarak isimlendirilir. Ayna örtüşmezliği ve parçacığın sağ veya sol-elli olma durumu tam olarak aynı şeye karşılık gelmez, ama yüksek enerjilerde yaklaşık olarak birbirlerine denktirler.
- Ayna örtüşmezliğini korunum yasası (chiral symmetry) sağ ve sol-elli parçacıkların birbirinden bağımsız olarak dönüşümlerini içerir.
- Yöney (vektör) korunum yasası (vector symmetry) aynı dönüşümlerin iki ayna örtüşmez duruma da uygulanmasıdır ve köşegen (diagonal) korunum yasası olarak da isimlendirilir.
- Eksensel (axial) korunum yasası sağ-elli parçacıklara sol-elli parçacıklara uygulanan dönüşümün tersinin uygulanması durumunda elde edilir.
Ek hatırlatmalar: çiftlenim (duality)
Daha önce bahsedildiği üzere asimtotik özgürlük yüksek enerjilerde (burada yüksek enerji aynı zamanda kısa mesafelere karşılık gelmektedir) parçacıklar arasında herhangi bir etkileşim olmamasıdır. Bu genelde alışılmış olan uzaklık arttıkça etkileşimin düşeceği düşüncesinin bir çiftlenimidir. 1971'de basit ayar değişmez kristal örgü (lattice) modelini geliştiren katı hal kuramcısı Franz Wegner, özgün modelin yüksek sıcaklıktaki yapısı çiftlenik modelin (dual model) düşük sıcaklıklardaki yapısına karşılık gelmektedir ve bu da açık olmayan bağdaşıklıkların asimtotik bozunumu olarak isimlendirilir. Buradaki yüksek sıcaklığın yapısı uzun mesafelerde bağdaşıklığın (correlation) güçlü kayboluşu ile düşük sıcaklığın yapısı ise neredeyse mükemmel düzenlemelerin kısa mesafelerdeki farklılıkları ile benzeştirilebilir. Burada Wegner modeli ile bir uyuşmazlık vardır ve sadece çiftlenik model bulunur. Bu da özgün modelde kuarkların dalganması gerekirken sadece bilinen çiftlenik modelde gluonların dalgalanması ile anlaşılabilir.
Gruplar ve korunum yasaları
Renkyükü grubu SU(3) yerel korunum yasalarından çıkmaktadır ve bunun ayar grubunun belirlenmesi ile KRD elde edilir. Elektrik yükünün sınıflandırılması ve yerel korunum yasalarının uygulanması U(1) grubunu verir ve bunun ayar grubunun belirlenmesi Kuantum elektrodevinimini (KED) verir, KED'de yer değiştirme özelliğine sahip bir gruptur. Eğer kütlesiz kuarklara göre Nf çeşnili KRD'nin uyarlanmış bir hali düşünülürse genel korunum yasasına sahip (ayna dönüşmez) çeşnili bir 
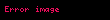
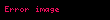

KRD'de iki farklı SU(3) (simetrisi) vardır. İlki kuarkların farklı renkyüklerine etki eder ve bu gluonların aracılık ettiği kesin bir ayar eşbakışımıdır (exact gauge symmetry). İkinci eşbakışım çeşni eşbakışımıdır ve SU(3) için üç tane çeşni düşünülür. Bu eşbakışım, çeşni SU(3), farklı kuark çeşnileri arasında dönüşümü sağlayan eşbakışımdır. Çeşni SU(3), KRD yokluğunun (QCD vacuum) yaklaşık bir eşbakışımdır ve temel bir eşbakışımdır. Bu eşbakışım, en hafif üç kuarkın kütlelerin küçüklüğünden kaynaklanır.
KRD boşluğunda kuarkların boşluk yoğuşumları gözlemlenir. Bunların kütleleri KRD ölçeğinden daha küçüktür. Bu yoğuşumlar yukarı kuarkı ve aşağı kuarkı içerir, acayip kuarkı da az bir oranda içerebilir ama diğer daha ağır olan kuarkları içermez. KRD boşluğu SU(2) dönüşümleri altında eşbakışımlıdır, yukarı ve aşağı kuarkın dönüşümleri durumu değiştirmez. Az bir oranda SU(3) eşbakışımı da gösterir, yukarı, aşağı ve acayip kuark dönüşümleri altında bazı drumlar için eşbakışım söz konusudur.
Yaklaşık çeşni eşbakışımları bağıl bozonlara sahiptir, rho ve omega gibi gözlemlenmiş parçacıklar, fakat bunlar sadece gluonlardır ve kütleleri vardır.
Lagrange işlevi
Kuarkların ve gluonların devinimi KRD Lagrange işlevi tarafından tarif edilir. Ayar değişmez KRD Lagrange işlevi:
burada 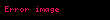
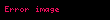
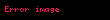
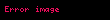
burada fabc SU(3) grubunun yapı sabitleridir. a, b veya c altimleri yukarı veya aşağı rahatlıkla değiştirilebilir, (+......+) gösterimine sahip olduklarından değişimleri kendilerine eşittir,fabc = fabc = fabc. Öte yandan μ veya ν altimlerinin yukarı veya aşağı hareketi (+---) gösterimine sahip olduklarından farklıdır ve ölçü gergisi (metric tensor) gereklidir..
Alanlar
Kuarklar, ölçüsü Kunatrum renk dinamiği olan renk yükünü taşıyan 1/2 fermion kütlesel örgülerdir. Kuarklar SU(3) ölçü grubunun temel temsilindeki Dirac alanlarla temsil edilir. Aynı zamanda elektrik yükü taşırlar ve zayıf isospin çiftlerinin bir kısmı olarak zayıf etkileşimlerine katılırlar. Her kuark için 1/3 olan baryon sayısını, aşırı yük ve çeşit kuatum sayılarından birini de içeren Global kuantum sayılarıı taşır.
SU(3)'ün bitişik temsilde yer aldıklarından, gluonlar aynı zamanda renk yüklerini taşıyan örgü bozonlardır. Elektrik yükleri yoktur, türleri yoktur ve zayıf etkileşimlere katılmazlar. Btün simetri gruplarının tekli temsillerinde yer alırlar.
Her kuarkın bir antikuarkı vardır. Her kuarkın yükü onu karşılayan zıt kuarkla aynıdır.
Dinamikler
Kuantum alan teorisinin kurallarına ve ilişkili Feynman diagramlarına göre, yukarıdaki teori üç basit etkileşimin ortaya çıkışına olanak sağlamıştır :kuark gluonu yayabilir veya absorbe edebilir, gluo bir gluonu yayabilir veya absorbe edebilir ve iki gluon doğrudan etkileşime girebilir. Bu durum, fotonların yükü olmadığından sadece tek bir etkileşime sahip olan kuantum renk dinamiği ile çelişir. Faddeev-Popov hayaletini de içeren diagramlar da değerlendirilir.
Alan Yasası ve Sınırlandırma
Yukarıda bahsedilen Lagrange ile detaylı hesaplamalar, kuark ve antikuarkın etkili potansiyel mezon, lastik bir bandın entropik elastikiyetine benzeyen uzak mesafelerdeki parçacık ve anti parçacık arasındaki etkileşimin bir çeşit sertliğini temsil eden 
Bu kuarkların hadronların içerisindeki sınırlandırılmasına yol açar, örneğin hadronların önceki toba modeline karşılık gelen tipik yarıçap Rc'li mezon ve nükleonlar gibi. Torba yarıçaplarının büyüklük sırası 1 fm (= 10−15 m). Dahası, yukarıda bahsedilen sertlik, nicelikli bir şekilde sıralı eşleme sabitlerinin kapalı döngü W çevresinde Wilson döngü ürününü PW nün beklenti değerinin alan kanunu tutumuna ilişkilidir. Örneğin,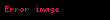
Yöntemler
Teori içeriğinin geniş analizi karmaşıktır. Kuantum renk dinamiğini çalışmak için birçok teknik geliştirilmiştir. Bazıları aşağıda özet bir şekilde anlatılmıştır.
Pertürbatif Kuantum Renk Dinamiği
Bu yaklaşım, pertubasyon teorisiniin yüksek enerji seviyelerinde doğru bir şekilde kullanılmasını sağlayan asomptik serbestliğe dayanır. Kapsam olarak sınırlı olsa da, bu yaklaşımla bugüne kadar kuatum renk dinamiğinde kesin sonuçlara varılmıştır.
Örgü Kuantum Renk Dinamiği
Kuantum renk dinamiğine pertübatif olmayan yaklaşımlar arasında, en köklü olanı örgü kuantum tekniğidir. Bu yaklaşım, devamlılık teorisinin analitik olarak zorlu yolunu, sadece bu amaç için geliştirilen QCDOC gibi sonradan super hesaplarda kullanmak üzere çok zor sayılı hesaplamalara azaltmak için uzay zamanı noktalarının ayrışık dizisini kullanır. Yavaş ve kaynak yoğunluklu bir yaklaşım olsa da, başka yöntemlerle ulaşılamaz olan teorinin kısımlarına, özellikle mezonda kuark ve antikuarklara arasındaki açık kuvvetlere, açıklama getirerek geniş bir uygulanması vardır. Yine de, sayısal işaret problemi, yüksek yoğunlukta ve düşük sıcaklıkta örgü metodunun kullanılmasını zorlaştırır. Örneğin nükleer madde veya nötron yıldızlarının içi gibi )
1/N Genişlemesi
Çok iyi bilinen bir yaklaşım şeması olan 1/N genişlemesi renk sayısının sonsuz olduğu öncülünden başlar ve bunun böyle olmadığını göstermek için bir dizi düzeltme yapar. Şu ana kadar, niceliksel tahmin yöntemi olmaktan çok niteliksel içgörü kaynağı olarak görülmüştür. Modern çeşitleri AdS/CFT yaklaşımını içerir.
Etkili Teoriler
Belli problemler için, belli sınırlarda niteliksel olarak doğru sonuçlar verebilen etkili teoriler yazılabilir. En iyi durumlarda, bunlar bazı Kuantum Renk Dinamiği Lagrangeside sistematik genişlemeler olarak elde edilebilir. Böyle etkili bir alan teorisi düşük enerjilerde Kuantum Renk Dinamiği etkili teorisini kiral perturbasyon teorisi ya da ChiPTdir. Daha net olarak, kuark kitlelerinin sıfıra eşit olduğu yerde tam bir simetri olan Kuantum Renk Dinamiğinin, spontane kiral simetri kırılmasında daha düşük enerji genişlemesidir, küçük kitlelere sahip olan u,d ve s kuarkı olmasa da, yine de iyi bir simetri yaklaşımıdır. Hafif olarak görüle Kuark sayısına bağlı olarak, SU(2) ChiPT veya SU(3) ChiPTsi kullanılır. Dİğer etkili teoriler ağır etkili kuark teorileri ve ince doğrudaş etkili teorileridir. Bu etkili teorilere ek olarak, Nambu-Jona-Lasinio modeli ve kiral modeli gibi modeller genel özellikleri tartışırken sıklıkla kullanılır.
Kuantum Renk Dinamiği Toplama Yasası
Operatör ürün genişlemesine dayanarak, değişik gözlemleri birbiriyle bağlayan ilişkiler dizisi elde edilebilir.
Nambu-Jona-Lasinio Modeli
Yakınlarda yapılan bir çalışmada, Kei-İchi Kondo düşük enerjili Kuantum Renk Dinamiği olarak türetmiştir, Polyakov–Nambu–Jona-Lasinio modelinin özellikle yerel olmayan şekli olduğundan, teori Nambu–Jona-Lasinio modeline bağlanmıştır. Daha sonra yerel şeklide, Polyakov döngü etkisinin olduğu Nambu–Jona-Lasinioda başka belli bir sınırlandırmayı tanımlamak içindir.
Nambu–Jona-Lasinio modeli kendi içinde birçok diğer şey arasında kullanılır çünkü Kuantum renk dinamiğinin kendisinde belli durumlara kadar var olan kiral simetri bozulmasının oldukça basit bir örneğidir. Bu modelde, yine de hiç sınırlama yoktur. Özellikle fiziksel vakumdaki izole edilmiş kuarkın enerjisi iyi tanımlanmış ve sonlu çıkar.
Deneysel Testler
Kuark çeşit kavramı, kuark modeli gelişiminde hadronların özelliklerini açıklarken duyulan gereklilikten ortaya sürülmüştür. Renk kavramı 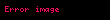
Kuarkların hadronların gerçek unsurları olduğuna ilk kanıt, SLAC'ta derin elastik olmayan saçılan deneylerde elde edilmiştir. Gluonlar için ilk kanıt PETRA'da 3 jet olayında gerçekleşmiştir.
Pertubatif Kuantum Renk Dinamiğinin varolduğuna birkaç iyi kanıt şunlardır :
- Kuantum Renk Dinamiği eşlemesinin çalışmasının birçok gözlemden çıkarılması
- Kutuplaştırılmış ve kutuplaştırılmamış derin elastik olmayan saçılmadaki ihlal ölçeklendirilmesi
- Çarpıştırıcılardaki vektör bozon üretimi
- Çarpıştırıcılardaki jet kesitleri
- LEP'de olay şekillendiren gözlemler
- Çarpıştırıcılardaki ağır kuark üretimi
Perturbatif olmayan Kuantum Renk Dinamiği testleri daha azdır, çünkü tahmin edebilmek zordur. Belki de en iyisi, ağır kuarkonyum spektrumlarının örgü hesaplamaları yoluyla Kuantum Renk Dinamiği eşlemesinin çalıştırılmasıdır. Ağır mezon kütlesi hakkında yeni bir iddia vardır. Diğer perturbatif olmayan testler şu anda en iyi yüzde beş seviyesindedir. Kütledeki devam eden çalışma ve hadronların yapı faktörleri ve zayıf matriks unsurları gelecek niceliksel testler için umut vadeden adaylardır. Tüm kuark madde ve kuark -gluon plazma, hala düzgün olarak işletilemeyen Kuantum Renk Dinamiği için bir test yatağıdır.
Kuantum Renk Dinamiğinin bir niteliksel tahmini de hala deneysel olarak gözlemlenemeyen glueballs adı verilen sadece gluonda yapılan kompozit parçacıklar olduğudu tahminidir. Kuantum Renk Dinamiği tarafından tahmin edilen özellikleri ile birlikte glueballun belli gözlemi teoriyi şiddetle kabul eder. Prensipte, eğer glueball gerçekten çıkartılırsa, bu Kuantum Renk Dinamiğini bitirmek için çok ciddii bir deney olurdu. Ama 2013 itibarıyla, parçacık hızlandırıcıları kendilerini üretebilmek için yeterli enerjiye sahip olsa da, bilim adamları tamamen hala glueballun varlığını kabul edemiyor veya inkâr edemiyor. Bu kuantum renk dinamiğinin tarihsel kısmında ele alınmıştır.
Katı Hal Fiziğine Çapraz İlişkiler
Katı hal fiziğine beklenmedik çapraz ilişkiler vardır. Örneğin, ölçü sabitliği kavramı, özellikle i =1,...,N, 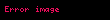

Burada εi ve εk miktarları, en basit ölçü dönüşümüne karşılık gelen 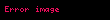

Ancak, burada Kuantum Renk Dinamiğinin gluonlara karşılık geldiği serbestliğin eşleşme dereceleri, sabit değerlere kesinleştirilmiştir. Bunun aksine, Kuantum renk dinamiğinde, dalgalanırlar ve serbest ölçü derecelerinin büyük sayısının içinde entropi önemli bir rol oynar.
Pozitif J0 için, Mattis devir gözlüğünün termodinamiği basit bir şekilde kılık değiştirmiş ferromagnete karşılık gelir. Çünkü bu sistemlerin engellenmesi yoktur. Bu terim, Mattis'in devir cam teorisinde basit bir ölçüdür. Niceliksel olarak kapalı döngüWboyunca döngü ürünü 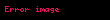
Döngü camının engelleme kavramı aslında Wilson'ın Kuantum renk dinamiği döngü miktarına benzer. Tek farklılık Kuantum Renk Dinamiğinin SU(3) matrislerini ele almasıdır ve birisinin dalgalanma miktarıyla ilgilenmesidir.
Engellemenin mükemmel eksikliği, döngü camı için olumsuz ve başka olmalıdır, bu döngü ürününün cezayi terimlerle Hamiltonian'a eklemesi gerekmesi demektir. Kuantum renk dinamiğinde Wilson döngüsü Lagrange için öncelikle gereklidir. Kuantum Renk Dinamiği ve düzensiz manyetik sistemler arasındaki ilişki Fradkin, Huberman ve Shenker'in ikilik kavramını vurgulayan çalışmasında ayrıca vurgulanmıştır.
Bir başka analoji, benzer şekilde bahsedilen, Wilson döngüsüne benzer olan, lastik bant entropi elastikliğinin oluşumu için önemli olan dolaşmış ağların göründüğü Polimer fiziğinde vardır. SU(3)'nün değişmeyen karakteri, böylece farklı döngü segmentlerini birleştiren önemsiz kimyasal bağlara karşılık gelir ve polimer analojide asomptik serbestlik kısa dalga limitidir. Örneğin 
Aynı zamanda Kuantum Renk dinamiğindeki sınırlama arasında bir yazışma vardır. Renk alanı sadece hadronların içinde sıfırdan farklıdır ve2. tip superiletkenlerin teori alanındaki genel manyetik alandaki tutumu şöyledir : Manyetizm, Abrikosov akış çizgisi örgüsünün içine sınırlandırılmıştır. Örneğin teorinin Londra nüfuz derinliği λ, kuantum kromodinamiğinin yarıçapı Rc nın sınırlanmasına benzerdir. Matematiksel olarak, bu yazışma Lagrange'nin rhs si üzerine ikinci terimle 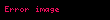
Kaynakça
- ^ J. Greensite (2011). An introduction to the confinement problem. Springer. .
- ^ H.D. Politzer (1973). "Reliable perturbative results for strong interactions". Physical Review Letters. 30 (26): 1346–1349. Bibcode:1973PhRvL..30.1346P. doi:10.1103/PhysRevLett.30.1346.
- ^ B. V. Struminsky, Magnetic moments of barions in the quark model. JINR-Preprint P-1939, Dubna, Russia. Submitted on January 7, 1965.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddedeki bilgilerin dogrulanabilmesi icin ek kaynaklar gerekli Lutfen guvenilir kaynaklar ekleyerek maddenin gelistirilmesine yardimci olun Kaynaksiz icerik itiraz konusu olabilir ve kaldirilabilir Kaynak ara Kuantum renk dinamigi haber gazete kitap akademik JSTOR Mart 2020 Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin Kuantum renk dinamigi veya kuantum kromodinamigi KRD veya KKD teorik fizikte kuantum kromodinamigi kuarklar ve gluonlar arasindaki guclu etkilesimin proton notron ve pion gibi kompozit hadronlari olusturan temel parcaciklarin teorisidir Ayni zamanda guclu etkilesim renkyuklu fermiyonlar olan kuarklarin SU 3 grubundaki takimindaki Yang Mills kurami ile de tanimlanabilir KRD degisme ozelligi olmayan a b b a displaystyle a times b neq b times a ayar kurami ile gosterilen ozel bir kuantum alanlar kuramidir Ayni zamanda KRD parcacik fiziginin standart modelinin onemli bir parcasidir Yillar boyunca oldukca buyuk bir miktarda KRD yi olumlayan deneysel veri toplanmistir KRD kendine has iki ozellige sahiptir Renkhapsi denilen birinci ozellik kuarklarin birbirinden ayrildikca onlari bir arada tutan kuvvetin yokolmamasidir Bu ozellikten dolayi iki kuarki birbirinden ayirmak sonsuz enerjiyi gerektirir Kuarklar hadronlarin icinde toplu bulunurlar ve yalniz basina gozlemlenmemistir Serbest kuark arastirmalarinin basarisizlikla sonuclanmasi KRD nin matametiksel analizi ile ispatlanmamasina ragmen renkhapsinin fizikciler tarafindan kabul edilen bir dusunce olmasina yol acmistir Diger taraftan renkhapsi olayi orgu KRD de lattice QCD gosterilebilmektedir Asimtotik ozgurluk denilin ikinci ozellik cok yuksek enerjili tepkimelerde kuarklarin ve gluonlarin cok zayif etkilesmesidir KRD nin bu tahmini 1970 lerde David Politzer Frank Wilczek ve David Gross tarafindan kesfedilmistir Bu calismalari bahsedilen biliminsanlarina 2004 Nobel fizik odulunu kazandirmistir Goreceli olarak dusuk enerjilerde renkhapsi baskin ozelliktir ve yuksek enerjilere cikildikca da asimtotik ozgurluk baskin ozelliktir Ama bu iki durumu ayiran gecis henuz anlasilmamistir EtimolojiKuark terimi 1929 da Murray Gell Mann tarafindan uydurulmustur Kuark kelimesinin temeli ise James Joyce un Finnegans Wake isimli kitabindaki Muster Mark icin uc kuark ifadesidir KRD nin uc yuku renkyuku olarak adlandirilir ve insanlarin gorebildigi uc renk olan kirmizi mavi ve yesil ile isimlendirilir Insanlarin gordugu renklerle KRD nin renkyukleri arasinda onemli bir benzerlik yoktur Tarihsel gelisimKabarcik odasi bubble chamber ve kivilcim odasinin spark chamber 1950 lerde icat edilmesi ile birlikte deneysel olarak parcacik fiziginde bircok hadron olarak isimlendirilen parcacik bulunmustur Gozlemlenen parcacik sayisinin coklugu hadronlarin tamaminin temel parcacik olamayacagi dusuncesini dogurmustur Oncelikle Eugene Wigner ve Werner Heisenberg tarafindan parcaciklar yuk ve izospin dusunulerek siniflandirilmistir Sonra 1953 te acayiplik strangeness ozelligine gore Murray Gell Mann ve Kazuhiko Nishijima tarafindan siniflandirilmistir Sezgisel algiyi arttirmak icin hadronlar benzer ozelliklerine ve kutlelerine gore sekiz katli olarak 1961 de Gell Mann ve Yuval Ne eman tarafindan siniflandirilmistir Gell Mann ve George Zweig Shoichi Skata nin yaklasimini duzelterek 1963 te bu siniflandirmalarin yapisinin uc farkli cesni ile tanimlanabilecek hadronlardan daha kucuk olan kuarklarla aciklanabildigini gostermislerdir Kuarklarin farkli bir kuantum sayisina daha sahip olabileceklerine dair ilk dusunce Boris Struminsky nin uc acayip strange kuarktan olusan W displaystyle Omega sss uzerine olan bir onyayininda kisa bir dipnot seklinde yazilmistir Bu parcacik uc acayip s kuarktan olusmustur ve spinleri ayni yondedir Ama bu durum kuantumun onemli ilkelerinden biri olan Pauli nin dislanma ilkesine terstir Bu dipnot su sekildedir Three identical quarks cannot form an antisymmetric S state In order to realize an antisymmetric orbital S state it is necessary for the quark to have an additional quantum number Uc ayni kuark antisimmetrik S durumunu olusturamazlar Bu antisimmetrik S durumunun olusturulabilmesi icin kuarklarin farkli bir kuantum sayisina sahip olmasi lazim B V Struminsky Magnetic moments of barions in the quark model JINR Preprint P 1939 Dubna Submitted on January 7 1965 Nikolay Bogolgov doktora ogrencisi olan Boris Struminsky ye bahsedilen arastirmayi yapmayi onermisti 1965 te Nikolay Bogolyubov Boris Struminsky ve Albert Tavchelidze kuarklarin bahsedilen kuantum serbestlik dereceleri uzerine yeni bir onyayin yaptilar Bu calisma Tavchelidze tarafindan diger calima arkadaslarinin iznini almadan Mayis 1965 te Trieste de Italya duzenlenen uluslararasi bir konferansta sunulmustur W displaystyle Omega ye benzer ilginc bir durum uc tane paralel spin yonelime sahip yukari up kuarktan olusan D displaystyle Delta baryonu uuu icin de gozlemlenmistir 1965 te Moo Young Han kendisinden bagimsiz calisan Yoichiro Nambu ve Oscar W Greenberg ile birlikte bu sorunu yaklasik olarak eszamanli bir sekilde kuarklarin diger kuantum mekaniksel parcaciklara gore fazladan bir kuantum sayisina sahip olduklarini soyleyerek cozmuslerdir Bu kuarklarin yeni kuantum sayisi SU 3 ayar takiminda renkyuku seklinde adlandirilan yeni bir serbestlik derecesine karsilik gelmektedir Han ve Nambu kuarklarin kendi aralarinda gluon denen ve sekizil yoney ayar bozonlari vector gauge boson araciligi ile etkilesebilecegini de soylemislerdir Serbest kuark arastirmalari surekli olarak basarisizlikla sonuclandigi icin ve o zamana kadar temel parcacik serbest bir sekilde gozlemlenebilir ve yalitilabilir seklinde tanimlandigindan dolayi Gell Mann siklikla kuarklarin cebirsel yapilar tanimina da gercek parcaciklar sinifina da uygun olmadigini soylemistir Gell Mann in soyledigi kuarklar hapsolmustur fakat guclu etkilesim de kuantum alanlar kurami seklinde tam olarak ifade edilmeyebilir cumlesiyle de anlatilabilir Kuarklarin hadronlar icinde hapsolmasi onlari o zamanin temel parcacik tanimina dahil edilememesi ve guclu etkilesimin tam olarak cebirsel bir kuramla anlasilamamasi durumu Gell Mann a bunlari soyletmistir Richard Feynman yuksek enerji deneylerinin kuarklarin gercek parcaciklar oldugunu gosterdigini soylemistir ve kuarklari partonlar seklinde isimlendirmistir Kuarklar hadronlarin parcalari oldugu icin bu sekilde isimlendirme yapmistir Feynman in parcacik tanimina gore temel parcaciklar bir yolu takip edebilen parcaciklardir Feynman in ve Gell Mann in yaklasimlari arasindaki fark kuramsal fizikciler arasinda derin bir ayrimla sonuclanmistir Feynman kuarklarin kuantum mekanigindeki diger parcaciklar gibi momentum ve konum dagilimina sahip oldugunu dusunmustur ve dogru bir sekilde parton momentumunun yayilmasinin kirinimsal sacilma ile aciklanabilecegine inanmistir Diger taraftan Gell Mann belirli kuark yuklerinin yerinin belirlenebilecegine inanmis ve kuarklarin yerinin uzay zaman kirilmasindan dolayi yerlerinin belirlenemeyecegi olasiligina da uzak kalmamistir Bu dusunce S dizey kuramindan daha asiri bir yaklasimdir James Bjorken noktasal parcacik seklindeki partonlarin elektronlarin protonlarla yaptiklari esnek olmayan carpismalarinda etkisini gosterecegini soylemistir ve bu tartismali bir sekilde 1969 da SLAC deneylerinde dogrulanmistir Bu sonuc fizikcilerin guclu etkilesim icin S dizeyi yaklasimini birakmalariyla sonuclanmistir David Gross David Politzer ve Frank Wilczek tarafindan guclu etkilesmede kesfi bircok yuksek enerji deneyinde kuantum alanlar kuraminin tedirgileme kurami perturbasyon kurami teknigini kullanarak cok hassas ongoruler yapmasina olanak saglamistir Gluonlara dair delil 1979 da PETRA daki gozlemlenmistir Bu deneyler gittikce hassaslasmistir ve su anki 2011 en hassas haline nin perturbative QCD dogrulanmasinda yuzde birkaclik oranla CERN in LEP kisminda ulasmistir Asimtotik ozgurlugun diger tarafinda renkhapsi bulunmaktadir Renkyukleri arasindaki kuvvet uzaklikla dusmedigi icin kuarklarin ve gluonlarin hadronlardan ayristirilamayacagina inanilmaktadir Kuramin bu yonu orgu KRD hesaplamalari ile dogrulanmistir Ama bu dogrulama cebirsel olarak yapilamamistir Clay matematik enstitusu tarafindan duyurulan Milenyum odullu sorunlardan biri de bu dogrulamadir Tedirgemeli olmayan non perturbative KRD nin diger calisilan konulari kuark gluon plazmanin da dahil oldugu kuark maddesinin halleridir KuramTanimlamalar Parcacik fizigindeki her alan kurami gozlemlerden cikarilmis olan doganin bazi korunum yasalari simetrileri uzerine kurulmustur Bunlar iki sinifa ayrilabilir Yerel korunum yasalari uzay zamanin her bir noktasinda diger noktalardan bagimsiz olarak korunan yasalardir Bu turdeki korunum yasalari ayar kuraminin temelidir ve kendine has ayar bozonlarinin kullanilmasini gerektirir Genel korunum yasalari bu turdeki korunum yasalarinin gecerliliginin uzay zamanin her noktasinda ayni anda olabilmesi gereklidir Kisaca A noktasindaki korunum baska bir B noktasinda da ayni anda saglanmalidir KRD SU 3 ayar takiminda bir ayar kuramidir ve bu renkyukunun bir yerel korunum yasasi olusturmasiyla elde edilmistir Guclu etkilesim farkli kuark cesnileri arasinda ayrim gozetmedigi icin KRD sadece kutle farklarindan dolayi korunmayan baska bir deyisle tam korunumu saglanmayan bir korunum yasasina sahiptir Enerjinin durumuna gore bazi kuark cesnilerinin etkilesimlerde aldiklari rol daha fazladir ve bu fark KRD de tamamiyla cesniler arasinda bahsedilen ve tamamiyla gecerli olmayan korunum yasasinin olusmasiyla sonuclanir Bunlara ek olarak baska genel korunum yasalari da vardir Bunlari tanimlayabilmemiz icin sag elli ve sol elli parcaciklar arasinda ayrim yapabilmemiz gerekmektedir Bunu tanimlamak icin de ayna ortusmezligi chirality kullanilir Eger parcacigin spini hareket yonune pozitif izdusum sagliyorsa sol elli negatif izdusum sagliyorsa da sag elli olarak isimlendirilir Ayna ortusmezligi ve parcacigin sag veya sol elli olma durumu tam olarak ayni seye karsilik gelmez ama yuksek enerjilerde yaklasik olarak birbirlerine denktirler Ayna ortusmezligini korunum yasasi chiral symmetry sag ve sol elli parcaciklarin birbirinden bagimsiz olarak donusumlerini icerir Yoney vektor korunum yasasi vector symmetry ayni donusumlerin iki ayna ortusmez duruma da uygulanmasidir ve kosegen diagonal korunum yasasi olarak da isimlendirilir Eksensel axial korunum yasasi sag elli parcaciklara sol elli parcaciklara uygulanan donusumun tersinin uygulanmasi durumunda elde edilir Ek hatirlatmalar ciftlenim duality Daha once bahsedildigi uzere asimtotik ozgurluk yuksek enerjilerde burada yuksek enerji ayni zamanda kisa mesafelere karsilik gelmektedir parcaciklar arasinda herhangi bir etkilesim olmamasidir Bu genelde alisilmis olan uzaklik arttikca etkilesimin dusecegi dusuncesinin bir ciftlenimidir 1971 de basit ayar degismez kristal orgu lattice modelini gelistiren kati hal kuramcisi Franz Wegner ozgun modelin yuksek sicakliktaki yapisi ciftlenik modelin dual model dusuk sicakliklardaki yapisina karsilik gelmektedir ve bu da acik olmayan bagdasikliklarin asimtotik bozunumu olarak isimlendirilir Buradaki yuksek sicakligin yapisi uzun mesafelerde bagdasikligin correlation guclu kaybolusu ile dusuk sicakligin yapisi ise neredeyse mukemmel duzenlemelerin kisa mesafelerdeki farkliliklari ile benzestirilebilir Burada Wegner modeli ile bir uyusmazlik vardir ve sadece ciftlenik model bulunur Bu da ozgun modelde kuarklarin dalganmasi gerekirken sadece bilinen ciftlenik modelde gluonlarin dalgalanmasi ile anlasilabilir Gruplar ve korunum yasalari Renkyuku grubu SU 3 yerel korunum yasalarindan cikmaktadir ve bunun ayar grubunun belirlenmesi ile KRD elde edilir Elektrik yukunun siniflandirilmasi ve yerel korunum yasalarinin uygulanmasi U 1 grubunu verir ve bunun ayar grubunun belirlenmesi Kuantum elektrodevinimini KED verir KED de yer degistirme ozelligine sahip bir gruptur Eger kutlesiz kuarklara gore Nf cesnili KRD nin uyarlanmis bir hali dusunulurse genel korunum yasasina sahip ayna donusmez cesnili bir SUL Nf SUR Nf UB 1 UA 1 displaystyle SU L N f times SU R N f times U B 1 times U A 1 grubu elde edilir Ayna ortusmezliginin korunmasi KRD nin temel boslugu tarafindan ayna ortusmez yogunlasmasiyla aniden yoneyli L R SUV Nf displaystyle SU V N f korunum grubuna kirilir Kuarklarin baryon sayisi UB 1 displaystyle U B 1 karsilik gelen yoney korunumu mutlak bir korunumdur Eksensel UA 1 displaystyle U A 1 korunumu kalsik fizikte mutlaktir fakat kuantumda korunmaz ve bu durum ayriklik olarak isimlendirilir Gluon alaninin olusturdugu dusunulen bu ayriklik ile ilgilidir KRD de iki farkli SU 3 simetrisi vardir Ilki kuarklarin farkli renkyuklerine etki eder ve bu gluonlarin aracilik ettigi kesin bir ayar esbakisimidir exact gauge symmetry Ikinci esbakisim cesni esbakisimidir ve SU 3 icin uc tane cesni dusunulur Bu esbakisim cesni SU 3 farkli kuark cesnileri arasinda donusumu saglayan esbakisimdir Cesni SU 3 KRD yoklugunun QCD vacuum yaklasik bir esbakisimdir ve temel bir esbakisimdir Bu esbakisim en hafif uc kuarkin kutlelerin kucuklugunden kaynaklanir KRD boslugunda kuarklarin bosluk yogusumlari gozlemlenir Bunlarin kutleleri KRD olceginden daha kucuktur Bu yogusumlar yukari kuarki ve asagi kuarki icerir acayip kuarki da az bir oranda icerebilir ama diger daha agir olan kuarklari icermez KRD boslugu SU 2 donusumleri altinda esbakisimlidir yukari ve asagi kuarkin donusumleri durumu degistirmez Az bir oranda SU 3 esbakisimi da gosterir yukari asagi ve acayip kuark donusumleri altinda bazi drumlar icin esbakisim soz konusudur Yaklasik cesni esbakisimlari bagil bozonlara sahiptir rho ve omega gibi gozlemlenmis parcaciklar fakat bunlar sadece gluonlardir ve kutleleri vardir Lagrange islevi Kuarklarin ve gluonlarin devinimi KRD Lagrange islevi tarafindan tarif edilir Ayar degismez KRD Lagrange islevi LQCD1 ps i igm Dm ij mdij psj 14GmnaGamn displaystyle mathcal L mathrm QCD 1 bar psi i left i gamma mu D mu ij m delta ij right psi j frac 1 4 G mu nu a G a mu nu dd burada i j displaystyle i j ldots altimleriyle indeks birlikte gosterilen psi x displaystyle psi i x kuark alanidir ve SU 3 ayar grubun temel gosteriminde uzay zamanda devinimli bir islevdir a b altimleriyle indeks birlikte gosterilen Gma x displaystyle G mu a x gluon alanina karsilik gelmektedir ve SU 3 ayar grubun bitistirilmis gosteriminde uzay zamanda devinimli bir islevdir gm Dirac dizeylerini gostermektedir ve Lorentz grubunun yoney gosterimlerini spinor gosterimlerine baglar Gmna displaystyle G mu nu a ayar degismez gluon alani kuvvet gergisidir tensor Bu Kuantum elektrodinamigindeki Fm n ye benzerdir ve asagidaki sekildedir Gmna mGna nGma gfabcGmbGnc displaystyle G mu nu a partial mu G nu a partial nu G mu a gf abc G mu b G nu c dd burada fabc SU 3 grubunun yapi sabitleridir a b veya c altimleri yukari veya asagi rahatlikla degistirilebilir gosterimine sahip olduklarindan degisimleri kendilerine esittir fabc fabc fa bc Ote yandan m veya n altimlerinin yukari veya asagi hareketi gosterimine sahip olduklarindan farklidir ve olcu gergisi metric tensor gereklidir Alanlar Kuarklar olcusu Kunatrum renk dinamigi olan renk yukunu tasiyan 1 2 fermion kutlesel orgulerdir Kuarklar SU 3 olcu grubunun temel temsilindeki Dirac alanlarla temsil edilir Ayni zamanda elektrik yuku tasirlar ve zayif isospin ciftlerinin bir kismi olarak zayif etkilesimlerine katilirlar Her kuark icin 1 3 olan baryon sayisini asiri yuk ve cesit kuatum sayilarindan birini de iceren Global kuantum sayilarii tasir SU 3 un bitisik temsilde yer aldiklarindan gluonlar ayni zamanda renk yuklerini tasiyan orgu bozonlardir Elektrik yukleri yoktur turleri yoktur ve zayif etkilesimlere katilmazlar Btun simetri gruplarinin tekli temsillerinde yer alirlar Her kuarkin bir antikuarki vardir Her kuarkin yuku onu karsilayan zit kuarkla aynidir Dinamikler Kuantum alan teorisinin kurallarina ve iliskili Feynman diagramlarina gore yukaridaki teori uc basit etkilesimin ortaya cikisina olanak saglamistir kuark gluonu yayabilir veya absorbe edebilir gluo bir gluonu yayabilir veya absorbe edebilir ve iki gluon dogrudan etkilesime girebilir Bu durum fotonlarin yuku olmadigindan sadece tek bir etkilesime sahip olan kuantum renk dinamigi ile celisir Faddeev Popov hayaletini de iceren diagramlar da degerlendirilir Alan Yasasi ve Sinirlandirma Yukarida bahsedilen Lagrange ile detayli hesaplamalar kuark ve antikuarkin etkili potansiyel mezon lastik bir bandin entropik elastikiyetine benzeyen uzak mesafelerdeki parcacik ve anti parcacik arasindaki etkilesimin bir cesit sertligini temsil eden r displaystyle propto r terimini icerdigini gosterir Bu kuarklarin hadronlarin icerisindeki sinirlandirilmasina yol acar ornegin hadronlarin onceki toba modeline karsilik gelen tipik yaricap Rc li mezon ve nukleonlar gibi Torba yaricaplarinin buyukluk sirasi 1 fm 10 15 m Dahasi yukarida bahsedilen sertlik nicelikli bir sekilde sirali esleme sabitlerinin kapali dongu W cevresinde Wilson dongu urununu PW nun beklenti degerinin alan kanunu tutumuna iliskilidir Ornegin PW displaystyle langle P W rangle dongu tarafindan kapatilan alana orantilidir Bu durum icin olcu grubununn degismeyen durumu temeldir YontemlerTeori iceriginin genis analizi karmasiktir Kuantum renk dinamigini calismak icin bircok teknik gelistirilmistir Bazilari asagida ozet bir sekilde anlatilmistir Perturbatif Kuantum Renk Dinamigi Bu yaklasim pertubasyon teorisiniin yuksek enerji seviyelerinde dogru bir sekilde kullanilmasini saglayan asomptik serbestlige dayanir Kapsam olarak sinirli olsa da bu yaklasimla bugune kadar kuatum renk dinamiginde kesin sonuclara varilmistir Orgu Kuantum Renk Dinamigi Kuantum renk dinamigine pertubatif olmayan yaklasimlar arasinda en koklu olani orgu kuantum teknigidir Bu yaklasim devamlilik teorisinin analitik olarak zorlu yolunu sadece bu amac icin gelistirilen QCDOC gibi sonradan super hesaplarda kullanmak uzere cok zor sayili hesaplamalara azaltmak icin uzay zamani noktalarinin ayrisik dizisini kullanir Yavas ve kaynak yogunluklu bir yaklasim olsa da baska yontemlerle ulasilamaz olan teorinin kisimlarina ozellikle mezonda kuark ve antikuarklara arasindaki acik kuvvetlere aciklama getirerek genis bir uygulanmasi vardir Yine de sayisal isaret problemi yuksek yogunlukta ve dusuk sicaklikta orgu metodunun kullanilmasini zorlastirir Ornegin nukleer madde veya notron yildizlarinin ici gibi 1 N Genislemesi Cok iyi bilinen bir yaklasim semasi olan 1 N genislemesi renk sayisinin sonsuz oldugu onculunden baslar ve bunun boyle olmadigini gostermek icin bir dizi duzeltme yapar Su ana kadar niceliksel tahmin yontemi olmaktan cok niteliksel icgoru kaynagi olarak gorulmustur Modern cesitleri AdS CFT yaklasimini icerir Etkili Teoriler Belli problemler icin belli sinirlarda niteliksel olarak dogru sonuclar verebilen etkili teoriler yazilabilir En iyi durumlarda bunlar bazi Kuantum Renk Dinamigi Lagrangeside sistematik genislemeler olarak elde edilebilir Boyle etkili bir alan teorisi dusuk enerjilerde Kuantum Renk Dinamigi etkili teorisini kiral perturbasyon teorisi ya da ChiPTdir Daha net olarak kuark kitlelerinin sifira esit oldugu yerde tam bir simetri olan Kuantum Renk Dinamiginin spontane kiral simetri kirilmasinda daha dusuk enerji genislemesidir kucuk kitlelere sahip olan u d ve s kuarki olmasa da yine de iyi bir simetri yaklasimidir Hafif olarak gorule Kuark sayisina bagli olarak SU 2 ChiPT veya SU 3 ChiPTsi kullanilir DIger etkili teoriler agir etkili kuark teorileri ve ince dogrudas etkili teorileridir Bu etkili teorilere ek olarak Nambu Jona Lasinio modeli ve kiral modeli gibi modeller genel ozellikleri tartisirken siklikla kullanilir Kuantum Renk Dinamigi Toplama Yasasi Operator urun genislemesine dayanarak degisik gozlemleri birbiriyle baglayan iliskiler dizisi elde edilebilir Nambu Jona Lasinio Modeli Yakinlarda yapilan bir calismada Kei Ichi Kondo dusuk enerjili Kuantum Renk Dinamigi olarak turetmistir Polyakov Nambu Jona Lasinio modelinin ozellikle yerel olmayan sekli oldugundan teori Nambu Jona Lasinio modeline baglanmistir Daha sonra yerel seklide Polyakov dongu etkisinin oldugu Nambu Jona Lasinioda baska belli bir sinirlandirmayi tanimlamak icindir Nambu Jona Lasinio modeli kendi icinde bircok diger sey arasinda kullanilir cunku Kuantum renk dinamiginin kendisinde belli durumlara kadar var olan kiral simetri bozulmasinin oldukca basit bir ornegidir Bu modelde yine de hic sinirlama yoktur Ozellikle fiziksel vakumdaki izole edilmis kuarkin enerjisi iyi tanimlanmis ve sonlu cikar Deneysel TestlerKuark cesit kavrami kuark modeli gelisiminde hadronlarin ozelliklerini aciklarken duyulan gereklilikten ortaya surulmustur Renk kavrami D displaystyle Delta puzzle dolayisiyla gerek duyulmustur Bu Kuantum Renk Dinamiginin tarihsel kisminda ele alinmistir Kuarklarin hadronlarin gercek unsurlari olduguna ilk kanit SLAC ta derin elastik olmayan sacilan deneylerde elde edilmistir Gluonlar icin ilk kanit PETRA da 3 jet olayinda gerceklesmistir Pertubatif Kuantum Renk Dinamiginin varolduguna birkac iyi kanit sunlardir Kuantum Renk Dinamigi eslemesinin calismasinin bircok gozlemden cikarilmasi Kutuplastirilmis ve kutuplastirilmamis derin elastik olmayan sacilmadaki ihlal olceklendirilmesi Carpistiricilardaki vektor bozon uretimi Carpistiricilardaki jet kesitleri LEP de olay sekillendiren gozlemler Carpistiricilardaki agir kuark uretimi Perturbatif olmayan Kuantum Renk Dinamigi testleri daha azdir cunku tahmin edebilmek zordur Belki de en iyisi agir kuarkonyum spektrumlarinin orgu hesaplamalari yoluyla Kuantum Renk Dinamigi eslemesinin calistirilmasidir Agir mezon kutlesi hakkinda yeni bir iddia vardir Diger perturbatif olmayan testler su anda en iyi yuzde bes seviyesindedir Kutledeki devam eden calisma ve hadronlarin yapi faktorleri ve zayif matriks unsurlari gelecek niceliksel testler icin umut vadeden adaylardir Tum kuark madde ve kuark gluon plazma hala duzgun olarak isletilemeyen Kuantum Renk Dinamigi icin bir test yatagidir Kuantum Renk Dinamiginin bir niteliksel tahmini de hala deneysel olarak gozlemlenemeyen glueballs adi verilen sadece gluonda yapilan kompozit parcaciklar oldugudu tahminidir Kuantum Renk Dinamigi tarafindan tahmin edilen ozellikleri ile birlikte glueballun belli gozlemi teoriyi siddetle kabul eder Prensipte eger glueball gercekten cikartilirsa bu Kuantum Renk Dinamigini bitirmek icin cok ciddii bir deney olurdu Ama 2013 itibariyla parcacik hizlandiricilari kendilerini uretebilmek icin yeterli enerjiye sahip olsa da bilim adamlari tamamen hala glueballun varligini kabul edemiyor veya inkar edemiyor Bu kuantum renk dinamiginin tarihsel kisminda ele alinmistir Kati Hal Fizigine Capraz IliskilerKati hal fizigine beklenmedik capraz iliskiler vardir Ornegin olcu sabitligi kavrami ozellikle i 1 N Ji k ϵiJ0ϵk displaystyle J i k epsilon i J 0 epsilon k icin duzenlenmis rastgele eslesmelerle iyi bilinen genellikle serbestligin devir derecesinde olan sistemlerden si 1 displaystyle s i pm 1 olan Mattis devir gozlugunun temelini olusturur Burada ei ve ek miktarlari en basit olcu donusumune karsilik gelen si si ϵiJi k ϵiJi kϵksk sk ϵk displaystyle s i to s i cdot epsilon i quad J i k to epsilon i J i k epsilon k quad s k to s k cdot epsilon k bagimsiz ve rastgele olarak 1 degerini alabilirler Bu demek oluyorki olculebilir miktarlarin termodinamik beklenti degerleri ornegin enerji H siJi ksk displaystyle mathcal H sum s i J i k s k degismezdir Ancak burada Kuantum Renk Dinamiginin gluonlara karsilik geldigi serbestligin eslesme dereceleri sabit degerlere kesinlestirilmistir Bunun aksine Kuantum renk dinamiginde dalgalanirlar ve serbest olcu derecelerinin buyuk sayisinin icinde entropi onemli bir rol oynar Pozitif J0 icin Mattis devir gozlugunun termodinamigi basit bir sekilde kilik degistirmis ferromagnete karsilik gelir Cunku bu sistemlerin engellenmesi yoktur Bu terim Mattis in devir cam teorisinde basit bir olcudur Niceliksel olarak kapali donguWboyunca dongu urunu PW Ji kJk l Jn mJm i displaystyle P W J i k J k l J n m J m i ile aynidir Yine de Mattis dongu cami icin gercek dongu camlariin aksine PW nin miktari asla negatif olmaz Dongu caminin engelleme kavrami aslinda Wilson in Kuantum renk dinamigi dongu miktarina benzer Tek farklilik Kuantum Renk Dinamiginin SU 3 matrislerini ele almasidir ve birisinin dalgalanma miktariyla ilgilenmesidir Engellemenin mukemmel eksikligi dongu cami icin olumsuz ve baska olmalidir bu dongu urununun cezayi terimlerle Hamiltonian a eklemesi gerekmesi demektir Kuantum renk dinamiginde Wilson dongusu Lagrange icin oncelikle gereklidir Kuantum Renk Dinamigi ve duzensiz manyetik sistemler arasindaki iliski Fradkin Huberman ve Shenker in ikilik kavramini vurgulayan calismasinda ayrica vurgulanmistir Bir baska analoji benzer sekilde bahsedilen Wilson dongusune benzer olan lastik bant entropi elastikliginin olusumu icin onemli olan dolasmis aglarin gorundugu Polimer fiziginde vardir SU 3 nun degismeyen karakteri boylece farkli dongu segmentlerini birlestiren onemsiz kimyasal baglara karsilik gelir ve polimer analojide asomptik serbestlik kisa dalga limitidir Ornegin 0 lw Rc displaystyle 0 leftarrow lambda w ll R c icin oldugu gibi Sistem kristalize oldugunda herhangi onemsiz korelasyon tamamen kaybolur Ayni zamanda Kuantum Renk dinamigindeki sinirlama arasinda bir yazisma vardir Renk alani sadece hadronlarin icinde sifirdan farklidir ve2 tip superiletkenlerin teori alanindaki genel manyetik alandaki tutumu soyledir Manyetizm Abrikosov akis cizgisi orgusunun icine sinirlandirilmistir Ornegin teorinin Londra nufuz derinligi l kuantum kromodinamiginin yaricapi Rc nin sinirlanmasina benzerdir Matematiksel olarak bu yazisma Lagrange nin rhs si uzerine ikinci terimle gGmaps igmTijapsj displaystyle propto gG mu a bar psi i gamma mu T ij a psi j desteklenir Kaynakca J Greensite 2011 An introduction to the confinement problem Springer ISBN 978 3 642 14381 6 H D Politzer 1973 Reliable perturbative results for strong interactions Physical Review Letters 30 26 1346 1349 Bibcode 1973PhRvL 30 1346P doi 10 1103 PhysRevLett 30 1346 B V Struminsky Magnetic moments of barions in the quark model JINR Preprint P 1939 Dubna Russia Submitted on January 7 1965
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans