Kuantum tüneli, parçacığın boyunca olan kuantum mekaniğini ifade eder. Bu, Güneş gibi yıldızlar dizisinde meydana gelen nükleer birleşmeler gibi birçok fiziksel olayda önemli bir rol oynar. , kuantum bilgisayarı ve taramalı tünelleme mikroskobu gibi modern araçlarda önemli uygulamaları vardır. Fiziksel olay olarak etkisi ve kabul görülürlüğü 20. yüzyılın başlarında ve ortalarına doğru geldiği tahmin ediliyor.
Tünelleme sıklıkla Heisenberg belirsizlik ilkesi ve maddenin dalga parçacık ikiliği kullanılarak açıklanır. Saf kuantum mekanik kavramlar olayın merkezindedir bu yüzden kuantum tüneli kuantum mekaniğinin yeni sonuçlarından biridir.
Tarih
Kuantum tüneli 1896 da Henri Becquerel tarafından keşfedilen radyoaktivite çalışmalarıyla geliştirilmiştir. Radyoaktivitenin ileriki çalışmaları 1903 yılında Nobel Fizik Ödülü'nü alan Marie Curie ve Pierre Curie tarafından incelenmiştir. Ernest Rutherford ve , daha sonra Friedrich Kohlrausch tarafından doğrulanmış olan doğası hakkında çalışmıştır. Yarı ömür fikri onların çalışmaları tarafından ortaya konulmuştur. , 1927'de çift kuyu potansiyelinin zemin durumunu incelediği zaman tünelin ilk farkına varandır. Matematikte ilk uygulaması 1928'de George Gamow, ve Edward Condon tarafından yapılan alfa bozunumu olmuştur. İki araştırmacı, tünelin matematiksel olasılığının direkt olarak ilişkili olduğu parçacığın yarı ömrü ve emilim enerjisinin arasındaki ilişkinin sürümünden ve nükleer potansiyeli için Schrödinger’in denklemini beklenmedik bir şekilde çözmüşlerdir.
Gamow tarafından verilen seminere katılımından sonra Max Born tünelin genelliliğinin farkına vardı. Born sadece nükleer fizikle kısıtlı olmadığını, birçok farklı sistem tarafından uygulanabilen, kuantum mekaniğinin genel bir sonucu olduğunun farkına vardı. Kısa bir süre sonra, iki grupta çekirdekteki parçacık durumlarını göz önüne aldı. Yarı iletkenler üzerindeki çalışmalar, transistörlerin geliştirilmesi ve diyotlar katılardaki elektron tünelinin varlığının kabulüne 1967 yılında yol açtı. Leo Esaki’nin çalışmaları, Ivar Giaever ve Brian Josephson’ın 1973 yılında Nobel Fizik Ödülü'nü alan süper iletken Cooper çiftlerinin tünelinin tahmin edilmesini sağladı.
Kavrama giriş


Kuantum tüneli kuantum boyutunda neler olduğunu çalışan kuantum mekaniği alanında başarısız olmaktadır. Bu süreç direkt olarak idrak edilemez fakat anlaşılması klasik mekaniğin yeterli kadar açıklanamadığı mikroskobik dünyada şekillenebilir. Olayı anlamak için potansiyel bariyerler arasında gezinmeye çalışan parçacıklar tepeden yuvarlanmaya çalışan bir topla karşılaştırılabilir. Bu senaryoda kuantum mekaniği ve klasik mekanik işleyiş bakımından birbirinden ayrılır. Klasik mekanik bariyerleri aşmak için yeterli enerjiye sahip olmayan parçacığın diğer tarafa ulaşamayacağını ön görür. Bu yüzden tepeyi aşmak için yeterli enerjisi olmayan top geri yuvarlanacaktır ya da duvarların arasından geçmek için yeterli enerjisi olmazsa geri sıçrama ya da bazı aykırı durumlarda kendini duvarın içine gömecektir. Kuantum mekaniğinde küçük bir ihtimalle de olsa bu parçacıklar- diğer tarafla tünel yapan- bariyerleri aşacaktır. Burada topu duvar veya yuvarlanılan tepeyi geçmek için ödünç alan olarak düşünebiliriz. Geri ödemesini elektronları ödünç aldığı halinden daha fazla enerjili bir şekilde yayarak yapacaktır. Kuantum mekaniğinde maddenin işleyişinden gelen bu farklılığın sebebi olarak dalga ve parçacıkların özelliklerini gösterilebilir. Bu ikilemin bir yorumunu parçacığın pozisyonunun ve momentumunun aynı anda bilenebileceğini de tanımlayan Heisenberg belirsizlik ilkesi içerir. Bu da çözüm sonsuza yaklaşırken sıfırın veya birin ihtimali ile sonucun olmayacağını söyler. Örneğin, bu konuma göre hesaplama 1 değerini alsın, diğeri, örneğin hızı sonsuz olabilir. Sonuç olarak diğer taraftaki parçacığın varlığının ihtimali sıfır olmayan bir değerdir ve bu tür parçacıklar benzer frekansla orantılı bir olasılıkla diğer tarafta gözükebilir.

 potansiyel bariyeri için Wigner fonksiyonu (atomik birim). Keskin çizgiler Hamiltonian seviyesi setini göstermektedir.
potansiyel bariyeri için Wigner fonksiyonu (atomik birim). Keskin çizgiler Hamiltonian seviyesi setini göstermektedir. .
.Tünelleme problemi
Parçacığın dalga fonksiyonu fiziksel sistemler hakkında bilinen her şeyi özetlemektedir. Buna göre kuantum mekaniğindeki problem sistemin dalga fonksiyonunun analizi etrafından yer bulmaktadır. Kuantum mekaniğinde Schrödinger denklemi gibi matematiksel formulasyonlar kullanılarak dalga fonksiyonları çözülebilir. Bu direkt olarak parçacığın pozisyonunun parçacığın her bir anındaki olasılığı olarak tanımlanan öz kütlesine bağlıdır. Büyük bariyerlerin sınırlarında, tünelleme olasılığı büyük ve geniş bariyerler için azalır.
Basit tünelleme bariyer modelleri için, örneğin dikdörtgen şeklindeki bariyerler, analitik sonuçları vardır. Problemler gerçek hayatta gerçek bir çözüme sahip değildirler bu yüzden bu tür problemlere yaklaşık sonuçlar verebilmek için yarı klasik metotlar geliştirilmektedir örneğin WKB yaklaşımı. İhtimaller Feynman’ın yol integral metodu ile seçmeli hassasiyetlerden sürülmektedir- hesaplamalı kaynaklar tarafından kısıtlandırılmış- bu tür hassasiyetler nadiren mühendislik uygulamasını gerektirir.
İlgili olaylar
Kuantum tünellemeyle aynı davranışlara sahip ve bu yüzden kolayca tünellemeyle tanımlanabilen birçok çeşitli olay vardır. Örnekler, klasik dalga parçacık iş birliğinin tünellenmesi, fani dalga kavramı(Maxwell denkleminin ışıkta uygulanması) ve bağımsız dala denkleminin dize dalgalar üzerinde uygulanması arasındadır. Fani dalga kavramı bu günlere kadar kuantum mekaniğinde tünelleme olarak adlandırıldı. Günümüzde ise farklı alanlarda kullanılmaktadır.
Bu modeller dikdörtgen bariyerlere benzer modellerle modellenmektedir. Bu tür durumlarda, aynı ve çok yakın sürede dala yayılması olan tek bir ulaştırma ortamı vardır. İkinci ortam ise dalgaların farklı yol izledikleri ortamdır. Bu ortam A ve ortam B’nin arasındaki ince farklılık olarak tanımlanabilir. Schrödinger’in denklemleri göz önünde bulundurularak yapılan dikdörtgen bariyerlerin analizleri A’ya giden dala çözümlerinin dalga denklemleri olarak sağlanabilir fakat gerçek çözüm B’deki üstel çözümüdür. Optikte, ortam A boşlukken ortam B camdır. Akustikte, ortam S sıvı veya gaz olabilir be ortam B katı olabilir. İki durumda da ortam A parçacığın toplam enerjisinin potansiyel enerjisinden büyük olduğu alandır ve ortam B potansiyel bariyerdir. Bunlar iki yönde de giren ve çıkış yapan dalgalara sahiptir. Birçok ortam ve bariyer olabilir ve bariyerler farklı olmak zorunda değillerdir, yaklaşımlar bu durumda kullanılabilir.
Uygulamaları
Tünelleme, 1,3 nm veya daha küçük incelikteki bariyerlerle meydana gelir. Fakat bu önemli önemli mikroskobik fiziksel olaylardır. Örneğin, tünelleme çok büyük ölçekli elektronik entegrasyonda bir akım kaynağının sızıntısıdır ve güç boşaltma, ısınma efektindeki örneğin, telefon teknolojisi ve yüksek hız gibi önemli sonuçları vardır. Bu bilgisayar çipinin nasıl küçük olabileceğinin en düşük sınırlı göstergesi olarak düşünülebilir.
Radyoaktif bozunma
Radyoaktif bozunma parçacıkların ve kararlı ürün oluşturmak için atomun kararsız çekirdeklerinden gelen enerjinin emilmesinin bir sürecidir. Bu olay parçacığın çekirdeğin tünellenmesiyle yapılır. (çekirdeğin içindeki elektron tünellemesi elektron yakalamasıdır.) Bu ilk yaklaşıma izin veren kuantum tünellemesinin ilk uygulamasıdır.
Anlık DNA mutasyonu
DNA’nın anlık mutasyonu, proton tünellemesi olarak tanımlanan kuantum mekaniğinde tek protonun yer değiştirmesinden sonra normal DNA nın kopyalanmasıyla meydana gelir. Hidrojen bağları DNA nın normal baz çiftlerine katılır. Potansiyel enerji bariyerleri tarafından ayrıştırılmış hidrojen bağları çift kuyu potansiyellerinde görülür.
Çift kuyu potansiyelinin proton dip kuyuda kalabilsin diye dip kuyu ile asimetrik olduğu bilinmektedir. Mutasyonun gerçekleştirilebilmesi için, protonun sığ potansiyel duvarlarından tünellenmesi gerekmektedir. Protonun düzenli pozisyonundan hareketi tatometrik geçiş olarak tanımlanır. Eğer DNA kopyalanması bu durumda yer alırsa DNA için baz eşleştirme kuralı mutasyona sebep olabilecek bir tehlike oluşturabilir. Per-Olov Lowdin, çift sarmalda(kuantum biyolojisi) anlık DNA mutasyon teorisini geliştiren ilk kişidir. Kuantum tünelleme-indükleme nin biyolojideki diğer örnekleri kanser ve yaşlanmaya neden olduğuna inanılmaktadır.
Soğuk emisyon
Elektronların soğuk emisyonu fizikte yarı iletken ve süper iletkenler ile ilgilidir. Elektronların düzensizce metal yüzeyinden akan gerilime doğru atladığı çünkü diğer bariyerlerden sıradan çarpışmalar süresince istatistiksel olarak daha çok enerjili oldukları termodinamik emisyon ile benzer şekildedir. Elektrik alan çok büyük olduğu zaman, tünelin atomik durumun dışında olarak elektronlar için yeterli olacak şekilde, akımın yaklaşık olarak elektrik alanla üstel biçimde belirtilebileceği şekilde geçmesine izin verir. Bu materyaller flash bellekler, vakum tüpleri ve elektron mikroskopları için önemlidirler.
Tünel kavşağı
Basit bir bariyer iki iletkenin ince bir yalıtkan ile ayrılmasından oluşturulabilir. Bunlar kuantum tünelinin çalışması için gerekli olan tünel kavşaklarıdır. Josephson kavşağı kuantum tünellemesinden fayda sağlar ve bazı yarı iletkenlerin süper iletkenliği Josephson kavşağı için oluşturulur. Güneş pili çoklu kavşağında da olduğu gibi bu manyetik alan ve hassas voltaj ölçümlerinde birçok uygulamaya sahiptir.

Tünel diyotu
Diyotlar elektrik akımının diğer yönlerden daha çok bir yöne gitmesini sağlayan elektrikli yarıiletken alettir. Bu alet amacına yönelik hizmet vermek için N tipi ve P tipi yarı iletken katmanlar arasındaki tükenme tabakasına dayanır. Bu ikisinin tükenme tabakasına ağır katkısı olduğu zaman tükenme tabaksı tünelleme için yeterince ince olabilir. Tünellemenin öneminden dolayı küçük bir sapma akıma uygulanır. Bunun maksimum enerjiye sahip olduğu yerde örneğin p ve n iletkenleri bağlar aynıdır. Gerilim arttıkça artık iletken bağlar sıralanamaz ve diyot tipik bir şekilde davranır.
Tünellenen akım hızlı şekilde aktığından dolayı, tünel diyotları gerilim aralığı artıp azalacak olan aralığa göre düzenlenir. Bu özellik bazı uygulamalarda kullanılır örneğin karakteristik tünelleme ihtimali gerilimin değişmesiyle değişir.
Rezonans tünelleme diyotu kuantum tünellemesini birçok benzer sonuçlara ulaşmak için de kullanılır. Diyot gerilimin ilerlemesi için fazla akımın bulunduğu yüksek enerjili iletkenlerin yan yana olduğu rezonans gerilimine de sahiptir. Bu en düşük enerji seviyesini gösteren kuantum potansiyel duvarını yaratır. Bu enerji elektronların enerjisinden daha yüksek olduğu zaman tünnelleme gerçekleşmez. İki gerilim enerjisinin hizalandığı anda elektronlar açık kablodaymış gibi akmaya başlar. Gerilim yükselirken tünelleme olanak dışı olmaya başlar ve ikinci enerji seviyesi fark edilebilir hale gelene kader diyot normal şekilde davranır.
Tünel-alan transistörü
Avrupa araştırma projesi kuantum tünellemesi ile kontrol edilen kanaların olduğu transistörün termal enjeksiyonlardan daha etkili bir alanı olduğunu gösterdi. Kanal gerilimini 1 volttan 0.2 volta ve güç tüketimini 100 kat daha azalttı. Eğer bu transistörler VLSI çipleri içinde büyütülürse performanslarını çok daha fazla geliştiriceklerdir.
Kuantum iletkenlikleri
Elektrik iletkenliğinin Drude modeli iletken metaldeki elektronların yapısı hakkında mükemmel tahminler yaparken, elektron çarpışmalarının doğasını anlamak için kuantum tünellemesi genişletilerek kullanılabilir. Serbest elektron paketleri bir dizi düzensiz dizilmiş bariyerle karşılaştığında %100 aktarma gerçekleşsin diye tüm bariyerler arasında bir müdahale olur. Teori şöyle söyler eğer dikdörtgen dizideki pozitif yüklü çekirdek metal boyunca tünnelencek serbest elektronlar yüksek derece de iletkenliğe izin verirler ve bu tür kirlilikler metali önemli derece de bozar.
Taramalı tünelleme mikroskobu
Taramalı tünelleme mikroskobu Gerd Binnig vr Heinrich Rohrer tarafından icat edilmiştir. Metal üzerindeki her bir atomu bireysel olarak gözlemleye izin verir. Uzaklık ile kuantum tünelleme arasındaki ilişkiden yararlanılarak kullanılır. Taramalı tünelleme mikroskobunun ucu iletken yüzeye çok yakın tutulduğu zaman, iğne ve yüzey arasındaki tünelleme elektron akımı ölçülerek bulunablir. Üzerine fazla miktarda gerilim uygulandığında ucunu aşabilen Piezoelektirk çubuk kullanılarak tünelleme akımını sabit bir düzeyde tutulabilir. Bu çubuklara uygulanabilen zamanla değişebilen gerilim kayıt edilebilir ve iletken yüzey fotoğraflanabilir. Taramalı tünelleme mikroskoplarının doğrulukları 0.001 nm veya %1 atomik yarıçaptadır.
Işıktan hızlı
Dönen sıfır parçacıkları için tünelleme anındaki seyahat ışık hızından fazla olacaktır. Görünüşe göre parçacığın ayrılmadan önce referans noktasına varacağı için nedensellik ilkesinin ihlali söz konusudur. Ancak dikkatle yapılan dalga paketlerinin aktarımının analizleri aslında görecelik ilkesinin ihlalinin olmadığını göstermektedir. 1988 de Francis E. Low sıfır zaman tünellemesini tekrar gözden geçirmiştir. Günümüzde yapılan fononlar, fotonlar ve elektronların deneysel tünellenmelerinin verileri Günter Nimtz tarafından yayınlanmıştır.
Kuantum tünellemesinin matematiksel yorumu
Aşağıdaki altbölümler kuantum tünellemesinin matematiksel formüllerini tartışmaktadır.
Schrödinger Denklemi
Tek boyutta zamandan bağımsız bir parçacık için Schrödinger denklemi şöyle yazılabilir
or
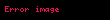
Bu denklemin çözümü faz sabiti –k veya k ile birlikte hareket eden dalgayı verir. Alternatif olarak eğer M(x) sabit ve pozitif ise, Schrödinger denklemi şu şekilde yazılır
Bu denklemin çözümü fani dalgalarda artan ya da azalan üstel yapıda olabilir. M(x) in pozisyon ile alakalı olduğu durumlarda, M(x) in pozitif veya negatif olmasına bağlı olarak aynı farklılıklar meydana gelir. Ardından M(x) in işareti ortamı belirler. Pozitif M(x) için ortam A tanımlanırken, negatif M(x) için ortam B tanımlanır. Bundan dolayı eğer pozitif M(x) in alanı iki negatif M(x)in alanı arasında sıkıştırılmışsa fani dalga kuramı oluşur ve bu da potansiyel bariyer yaratır.
Bu olay M(x) in x e bağlı çok karmaşık durumlarda olduğu matematikte, bazı özel durumlar hariç, fiziksel gerçekçilikte karşılık bulamamaktadır. Yarı klasik metotların fizik kitaplarında olduğu gibi tartışımı diğer bölümde verilecektir. Tamamı ile ve karmaşık matematiksel işlemler 1965 yılında Fröman tarafından ortaya çıkmıştır. Fikirleri fizik kitaplarında anonim değildir fakat düzeltmeleri nicel efektler taşır.
WKB yaklaşımı
Dalga fonksiyonu üstel bir fonksiyon olarak açıklanır.
, where

, A(x) B(x) gerçek değerli fonksiyonlar için.
İkinci denklemi birinci denklemin içine yerleştirerek ve hayali kısmın bölümünü kullanarak
.
Bu denklemi çözmek için her iki kısımda yarı klasik yaklaşımlar yapılarak 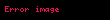

ve
,
En düşük mertebeden terimler ile aşağıdakiler takip etmekte,
ve
.
Bu noktada iki aşırı durum hesaba katılabilir. ‘’’Durum 1’’’ Eğer faz 
Klasik hareket içindir. Genişleme verimin bir sonraki mertebesi ile tekrar çözümü
‘’’durum 2’’’ Eğer genliğine kıyasla faz yavaş şekilde değişirse 
Tünellemeye karşılık gelir. Genişleme veriminin bir sonraki mertebesi ile tekrar çözümü
İki durumda da paydalardan görülmektedir ki iki yaklaşık çözümlerde klasik dönüm noktası E=V(x) e yakındır. Potansiyel tepeden uzakta parçacık serbest ve salınım yapan dalgaya benzer davranır, potansiyel tepenin altında, parçacık genlik içinde üstel değişikliklere gider. Bu limitlerde parçacığın davranışlarını hesaba katarak ve klasik dönüş noktalarını hesaba katarak genel bir çözüm yapılabilir. Başlangıç için klasik dönüş noktası 


Birinci dereceden terim tutulması doğrusallık sağlar:
.
Bu yaklaşım kullanılarak, 
.
Çözüm olarak Airy fonksiyon kullanılarak bu denklem çözülebilir.
Bu çözümleri tüm klasik dönüm noktaları için alarak sınırlı çözümlerle bağlantılı genel bir sonuç elde edilebilir. Klasik dönüm noktasının bir tarafında verilen 2 katsayı,diğer tarafında verilen 2 katsayı kullanılarak bunların birleştirilerek elde edilen sonucuyla karar verilebilir. Sonuç olarak, Airy fonksiyon çözümü sinüsün kosünüsün ve üstel fonksiyonun belirli sınırlar içinde asimptotu olur. 

ve
Katsayının bulunmasıyla genel çözüm bulunabilir. Böylece tek bariyer boyunca tünellenen parçacığın dağıtım katsayısı
,

.
Konuyla ilgili yayınlar
- N. Fröman and P.-O. Fröman (1965). JWKB Approximation: Contributions to the Theory. Amsterdam: North-Holland.
- Razavy, Mohsen (2003). Quantum Theory of Tunneling. World Scientific. ISBN .
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2.2 yayıncı=Prentice Hall bas.). ISBN .
- and Skinner, D. (2010). The Physics of Quantum Mechanics: An Introduction (3.3 yayıncı=Cappella Archive bas.). ISBN .
- (2002). Introductory Quantum Mechanics. Addison-Wesley. ISBN .
- Vilenkin, Alexander; Vilenkin, Alexander; Winitzki, Serge (2003). "Particle creation in a tunneling universe". Physical Review D. 68 (2). s. 023520. arXiv:gr-qc/0210034 $2. Bibcode:2003PhRvD..68b3520H. doi:10.1103/PhysRevD.68.023520.
Dış bağlantılar
- Animation, applications and research linked to tunnel effect and other quantum phenomena25 Mayıs 2012 tarihinde Wayback Machine sitesinde . (Université Paris Sud)
- Animated illustration of quantum tunnelling 9 Ocak 2015 tarihinde Wayback Machine sitesinde .
- Animated illustration of quantum tunnelling in a RTD device 20 Mart 2015 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Kuantum tuneli parcacigin boyunca olan kuantum mekanigini ifade eder Bu Gunes gibi yildizlar dizisinde meydana gelen nukleer birlesmeler gibi bircok fiziksel olayda onemli bir rol oynar kuantum bilgisayari ve taramali tunelleme mikroskobu gibi modern araclarda onemli uygulamalari vardir Fiziksel olay olarak etkisi ve kabul gorulurlugu 20 yuzyilin baslarinda ve ortalarina dogru geldigi tahmin ediliyor Tunelleme siklikla Heisenberg belirsizlik ilkesi ve maddenin dalga parcacik ikiligi kullanilarak aciklanir Saf kuantum mekanik kavramlar olayin merkezindedir bu yuzden kuantum tuneli kuantum mekaniginin yeni sonuclarindan biridir TarihKuantum tuneli 1896 da Henri Becquerel tarafindan kesfedilen radyoaktivite calismalariyla gelistirilmistir Radyoaktivitenin ileriki calismalari 1903 yilinda Nobel Fizik Odulu nu alan Marie Curie ve Pierre Curie tarafindan incelenmistir Ernest Rutherford ve daha sonra Friedrich Kohlrausch tarafindan dogrulanmis olan dogasi hakkinda calismistir Yari omur fikri onlarin calismalari tarafindan ortaya konulmustur 1927 de cift kuyu potansiyelinin zemin durumunu inceledigi zaman tunelin ilk farkina varandir Matematikte ilk uygulamasi 1928 de George Gamow ve Edward Condon tarafindan yapilan alfa bozunumu olmustur Iki arastirmaci tunelin matematiksel olasiliginin direkt olarak iliskili oldugu parcacigin yari omru ve emilim enerjisinin arasindaki iliskinin surumunden ve nukleer potansiyeli icin Schrodinger in denklemini beklenmedik bir sekilde cozmuslerdir Gamow tarafindan verilen seminere katilimindan sonra Max Born tunelin genelliliginin farkina vardi Born sadece nukleer fizikle kisitli olmadigini bircok farkli sistem tarafindan uygulanabilen kuantum mekaniginin genel bir sonucu oldugunun farkina vardi Kisa bir sure sonra iki grupta cekirdekteki parcacik durumlarini goz onune aldi Yari iletkenler uzerindeki calismalar transistorlerin gelistirilmesi ve diyotlar katilardaki elektron tunelinin varliginin kabulune 1967 yilinda yol acti Leo Esaki nin calismalari Ivar Giaever ve Brian Josephson in 1973 yilinda Nobel Fizik Odulu nu alan super iletken Cooper ciftlerinin tunelinin tahmin edilmesini sagladi Kavrama giris source source source source source source source track track Animasyon tunel efektini ve onun uygulamasini gostermektedirBariyer boyunca kuantum tuneli Tuneldeki parcaciklarin enerjileri esit fakat genlikleri giderek azalmakta Bariyer boyunca kuantum tuneli Orijinde x 0 yuksek ama sinirli potansiyel bariyer Onemli tunel efekti gorulmektedir Kuantum tuneli kuantum boyutunda neler oldugunu calisan kuantum mekanigi alaninda basarisiz olmaktadir Bu surec direkt olarak idrak edilemez fakat anlasilmasi klasik mekanigin yeterli kadar aciklanamadigi mikroskobik dunyada sekillenebilir Olayi anlamak icin potansiyel bariyerler arasinda gezinmeye calisan parcaciklar tepeden yuvarlanmaya calisan bir topla karsilastirilabilir Bu senaryoda kuantum mekanigi ve klasik mekanik isleyis bakimindan birbirinden ayrilir Klasik mekanik bariyerleri asmak icin yeterli enerjiye sahip olmayan parcacigin diger tarafa ulasamayacagini on gorur Bu yuzden tepeyi asmak icin yeterli enerjisi olmayan top geri yuvarlanacaktir ya da duvarlarin arasindan gecmek icin yeterli enerjisi olmazsa geri sicrama ya da bazi aykiri durumlarda kendini duvarin icine gomecektir Kuantum mekaniginde kucuk bir ihtimalle de olsa bu parcaciklar diger tarafla tunel yapan bariyerleri asacaktir Burada topu duvar veya yuvarlanilan tepeyi gecmek icin odunc alan olarak dusunebiliriz Geri odemesini elektronlari odunc aldigi halinden daha fazla enerjili bir sekilde yayarak yapacaktir Kuantum mekaniginde maddenin isleyisinden gelen bu farkliligin sebebi olarak dalga ve parcaciklarin ozelliklerini gosterilebilir Bu ikilemin bir yorumunu parcacigin pozisyonunun ve momentumunun ayni anda bilenebilecegini de tanimlayan Heisenberg belirsizlik ilkesi icerir Bu da cozum sonsuza yaklasirken sifirin veya birin ihtimali ile sonucun olmayacagini soyler Ornegin bu konuma gore hesaplama 1 degerini alsin digeri ornegin hizi sonsuz olabilir Sonuc olarak diger taraftaki parcacigin varliginin ihtimali sifir olmayan bir degerdir ve bu tur parcaciklar benzer frekansla orantili bir olasilikla diger tarafta gozukebilir Elektron dalgasi potansiyel bariyerle direkt orantilidir Sagdaki sonuk lambalar tunel elektronlarini gostermektedir source source source source source source Faz uzayi formulasyonunda kuantum mekanigi U x 8e 0 25x2 displaystyle U x 8e 0 25x 2 potansiyel bariyeri icin Wigner fonksiyonu atomik birim Keskin cizgiler Hamiltonian seviyesi setini gostermektedir H x p p2 2 U x displaystyle H x p p 2 2 U x Tunelleme problemiParcacigin dalga fonksiyonu fiziksel sistemler hakkinda bilinen her seyi ozetlemektedir Buna gore kuantum mekanigindeki problem sistemin dalga fonksiyonunun analizi etrafindan yer bulmaktadir Kuantum mekaniginde Schrodinger denklemi gibi matematiksel formulasyonlar kullanilarak dalga fonksiyonlari cozulebilir Bu direkt olarak parcacigin pozisyonunun parcacigin her bir anindaki olasiligi olarak tanimlanan oz kutlesine baglidir Buyuk bariyerlerin sinirlarinda tunelleme olasiligi buyuk ve genis bariyerler icin azalir Basit tunelleme bariyer modelleri icin ornegin dikdortgen seklindeki bariyerler analitik sonuclari vardir Problemler gercek hayatta gercek bir cozume sahip degildirler bu yuzden bu tur problemlere yaklasik sonuclar verebilmek icin yari klasik metotlar gelistirilmektedir ornegin WKB yaklasimi Ihtimaller Feynman in yol integral metodu ile secmeli hassasiyetlerden surulmektedir hesaplamali kaynaklar tarafindan kisitlandirilmis bu tur hassasiyetler nadiren muhendislik uygulamasini gerektirir Ilgili olaylarKuantum tunellemeyle ayni davranislara sahip ve bu yuzden kolayca tunellemeyle tanimlanabilen bircok cesitli olay vardir Ornekler klasik dalga parcacik is birliginin tunellenmesi fani dalga kavrami Maxwell denkleminin isikta uygulanmasi ve bagimsiz dala denkleminin dize dalgalar uzerinde uygulanmasi arasindadir Fani dalga kavrami bu gunlere kadar kuantum mekaniginde tunelleme olarak adlandirildi Gunumuzde ise farkli alanlarda kullanilmaktadir Bu modeller dikdortgen bariyerlere benzer modellerle modellenmektedir Bu tur durumlarda ayni ve cok yakin surede dala yayilmasi olan tek bir ulastirma ortami vardir Ikinci ortam ise dalgalarin farkli yol izledikleri ortamdir Bu ortam A ve ortam B nin arasindaki ince farklilik olarak tanimlanabilir Schrodinger in denklemleri goz onunde bulundurularak yapilan dikdortgen bariyerlerin analizleri A ya giden dala cozumlerinin dalga denklemleri olarak saglanabilir fakat gercek cozum B deki ustel cozumudur Optikte ortam A boslukken ortam B camdir Akustikte ortam S sivi veya gaz olabilir be ortam B kati olabilir Iki durumda da ortam A parcacigin toplam enerjisinin potansiyel enerjisinden buyuk oldugu alandir ve ortam B potansiyel bariyerdir Bunlar iki yonde de giren ve cikis yapan dalgalara sahiptir Bircok ortam ve bariyer olabilir ve bariyerler farkli olmak zorunda degillerdir yaklasimlar bu durumda kullanilabilir UygulamalariTunelleme 1 3 nm veya daha kucuk incelikteki bariyerlerle meydana gelir Fakat bu onemli onemli mikroskobik fiziksel olaylardir Ornegin tunelleme cok buyuk olcekli elektronik entegrasyonda bir akim kaynaginin sizintisidir ve guc bosaltma isinma efektindeki ornegin telefon teknolojisi ve yuksek hiz gibi onemli sonuclari vardir Bu bilgisayar cipinin nasil kucuk olabileceginin en dusuk sinirli gostergesi olarak dusunulebilir Radyoaktif bozunmaRadyoaktif bozunma parcaciklarin ve kararli urun olusturmak icin atomun kararsiz cekirdeklerinden gelen enerjinin emilmesinin bir surecidir Bu olay parcacigin cekirdegin tunellenmesiyle yapilir cekirdegin icindeki elektron tunellemesi elektron yakalamasidir Bu ilk yaklasima izin veren kuantum tunellemesinin ilk uygulamasidir Anlik DNA mutasyonuDNA nin anlik mutasyonu proton tunellemesi olarak tanimlanan kuantum mekaniginde tek protonun yer degistirmesinden sonra normal DNA nin kopyalanmasiyla meydana gelir Hidrojen baglari DNA nin normal baz ciftlerine katilir Potansiyel enerji bariyerleri tarafindan ayristirilmis hidrojen baglari cift kuyu potansiyellerinde gorulur Cift kuyu potansiyelinin proton dip kuyuda kalabilsin diye dip kuyu ile asimetrik oldugu bilinmektedir Mutasyonun gerceklestirilebilmesi icin protonun sig potansiyel duvarlarindan tunellenmesi gerekmektedir Protonun duzenli pozisyonundan hareketi tatometrik gecis olarak tanimlanir Eger DNA kopyalanmasi bu durumda yer alirsa DNA icin baz eslestirme kurali mutasyona sebep olabilecek bir tehlike olusturabilir Per Olov Lowdin cift sarmalda kuantum biyolojisi anlik DNA mutasyon teorisini gelistiren ilk kisidir Kuantum tunelleme indukleme nin biyolojideki diger ornekleri kanser ve yaslanmaya neden olduguna inanilmaktadir Soguk emisyonElektronlarin soguk emisyonu fizikte yari iletken ve super iletkenler ile ilgilidir Elektronlarin duzensizce metal yuzeyinden akan gerilime dogru atladigi cunku diger bariyerlerden siradan carpismalar suresince istatistiksel olarak daha cok enerjili olduklari termodinamik emisyon ile benzer sekildedir Elektrik alan cok buyuk oldugu zaman tunelin atomik durumun disinda olarak elektronlar icin yeterli olacak sekilde akimin yaklasik olarak elektrik alanla ustel bicimde belirtilebilecegi sekilde gecmesine izin verir Bu materyaller flash bellekler vakum tupleri ve elektron mikroskoplari icin onemlidirler Tunel kavsagiBasit bir bariyer iki iletkenin ince bir yalitkan ile ayrilmasindan olusturulabilir Bunlar kuantum tunelinin calismasi icin gerekli olan tunel kavsaklaridir Josephson kavsagi kuantum tunellemesinden fayda saglar ve bazi yari iletkenlerin super iletkenligi Josephson kavsagi icin olusturulur Gunes pili coklu kavsaginda da oldugu gibi bu manyetik alan ve hassas voltaj olcumlerinde bircok uygulamaya sahiptir Rezonans tunelleme cihazinin potansiyel bariyerler boyunca kuantum tunellemesi olayina bagli calisma mekanizmasi Tunel diyotuDiyotlar elektrik akiminin diger yonlerden daha cok bir yone gitmesini saglayan elektrikli yariiletken alettir Bu alet amacina yonelik hizmet vermek icin N tipi ve P tipi yari iletken katmanlar arasindaki tukenme tabakasina dayanir Bu ikisinin tukenme tabakasina agir katkisi oldugu zaman tukenme tabaksi tunelleme icin yeterince ince olabilir Tunellemenin oneminden dolayi kucuk bir sapma akima uygulanir Bunun maksimum enerjiye sahip oldugu yerde ornegin p ve n iletkenleri baglar aynidir Gerilim arttikca artik iletken baglar siralanamaz ve diyot tipik bir sekilde davranir Tunellenen akim hizli sekilde aktigindan dolayi tunel diyotlari gerilim araligi artip azalacak olan araliga gore duzenlenir Bu ozellik bazi uygulamalarda kullanilir ornegin karakteristik tunelleme ihtimali gerilimin degismesiyle degisir Rezonans tunelleme diyotu kuantum tunellemesini bircok benzer sonuclara ulasmak icin de kullanilir Diyot gerilimin ilerlemesi icin fazla akimin bulundugu yuksek enerjili iletkenlerin yan yana oldugu rezonans gerilimine de sahiptir Bu en dusuk enerji seviyesini gosteren kuantum potansiyel duvarini yaratir Bu enerji elektronlarin enerjisinden daha yuksek oldugu zaman tunnelleme gerceklesmez Iki gerilim enerjisinin hizalandigi anda elektronlar acik kablodaymis gibi akmaya baslar Gerilim yukselirken tunelleme olanak disi olmaya baslar ve ikinci enerji seviyesi fark edilebilir hale gelene kader diyot normal sekilde davranir Tunel alan transistoruAvrupa arastirma projesi kuantum tunellemesi ile kontrol edilen kanalarin oldugu transistorun termal enjeksiyonlardan daha etkili bir alani oldugunu gosterdi Kanal gerilimini 1 volttan 0 2 volta ve guc tuketimini 100 kat daha azaltti Eger bu transistorler VLSI cipleri icinde buyutulurse performanslarini cok daha fazla gelistiriceklerdir Kuantum iletkenlikleriElektrik iletkenliginin Drude modeli iletken metaldeki elektronlarin yapisi hakkinda mukemmel tahminler yaparken elektron carpismalarinin dogasini anlamak icin kuantum tunellemesi genisletilerek kullanilabilir Serbest elektron paketleri bir dizi duzensiz dizilmis bariyerle karsilastiginda 100 aktarma gerceklessin diye tum bariyerler arasinda bir mudahale olur Teori soyle soyler eger dikdortgen dizideki pozitif yuklu cekirdek metal boyunca tunnelencek serbest elektronlar yuksek derece de iletkenlige izin verirler ve bu tur kirlilikler metali onemli derece de bozar Taramali tunelleme mikroskobuTaramali tunelleme mikroskobu Gerd Binnig vr Heinrich Rohrer tarafindan icat edilmistir Metal uzerindeki her bir atomu bireysel olarak gozlemleye izin verir Uzaklik ile kuantum tunelleme arasindaki iliskiden yararlanilarak kullanilir Taramali tunelleme mikroskobunun ucu iletken yuzeye cok yakin tutuldugu zaman igne ve yuzey arasindaki tunelleme elektron akimi olculerek bulunablir Uzerine fazla miktarda gerilim uygulandiginda ucunu asabilen Piezoelektirk cubuk kullanilarak tunelleme akimini sabit bir duzeyde tutulabilir Bu cubuklara uygulanabilen zamanla degisebilen gerilim kayit edilebilir ve iletken yuzey fotograflanabilir Taramali tunelleme mikroskoplarinin dogruluklari 0 001 nm veya 1 atomik yaricaptadir Isiktan hizliDonen sifir parcaciklari icin tunelleme anindaki seyahat isik hizindan fazla olacaktir Gorunuse gore parcacigin ayrilmadan once referans noktasina varacagi icin nedensellik ilkesinin ihlali soz konusudur Ancak dikkatle yapilan dalga paketlerinin aktariminin analizleri aslinda gorecelik ilkesinin ihlalinin olmadigini gostermektedir 1988 de Francis E Low sifir zaman tunellemesini tekrar gozden gecirmistir Gunumuzde yapilan fononlar fotonlar ve elektronlarin deneysel tunellenmelerinin verileri Gunter Nimtz tarafindan yayinlanmistir Kuantum tunellemesinin matematiksel yorumuAsagidaki altbolumler kuantum tunellemesinin matematiksel formullerini tartismaktadir Schrodinger DenklemiTek boyutta zamandan bagimsiz bir parcacik icin Schrodinger denklemi soyle yazilabilir ℏ22md2dx2PS x V x PS x EPS x displaystyle frac hbar 2 2m frac d 2 dx 2 Psi x V x Psi x E Psi x ord2dx2PS x 2mℏ2 V x E PS x 2mℏ2M x PS x displaystyle frac d 2 dx 2 Psi x frac 2m hbar 2 left V x E right Psi x equiv frac 2m hbar 2 M x Psi x ℏ displaystyle hbar Planck sabitidir m parcacigin kutlesi x parcacigin hareketi yonundeki mesafesi PS Schrodinger dalga fonksiyonu V parcacigin potansiyel enerjisi uygun olan herhangi bir referans noktasina gore olculen E parcacigin x eksenindeki hareketiyle alakali enerjisi ve M x V x tarafindan tanimlanan fizikte henuz bi ismi olmayan bir niceldir M x in pozitif veya negatif degerli olmasina gore degisen Schrodinger in denklemi farkli her x degeri icin farkli bir deger alabilir Eger M x sabit ve negatif olursa Schrodinger denklemi su formda yazilir d2dx2PS x 2mℏ2M x PS x k2PS x wherek2 2mℏ2M displaystyle frac d 2 dx 2 Psi x frac 2m hbar 2 M x Psi x k 2 Psi x mathrm where k 2 frac 2m hbar 2 M Bu denklemin cozumu faz sabiti k veya k ile birlikte hareket eden dalgayi verir Alternatif olarak eger M x sabit ve pozitif ise Schrodinger denklemi su sekilde yazilir d2dx2PS x 2mℏ2M x PS x k2PS x wherek2 2mℏ2M displaystyle frac d 2 dx 2 Psi x frac 2m hbar 2 M x Psi x kappa 2 Psi x mathrm where kappa 2 frac 2m hbar 2 M Bu denklemin cozumu fani dalgalarda artan ya da azalan ustel yapida olabilir M x in pozisyon ile alakali oldugu durumlarda M x in pozitif veya negatif olmasina bagli olarak ayni farkliliklar meydana gelir Ardindan M x in isareti ortami belirler Pozitif M x icin ortam A tanimlanirken negatif M x icin ortam B tanimlanir Bundan dolayi eger pozitif M x in alani iki negatif M x in alani arasinda sikistirilmissa fani dalga kurami olusur ve bu da potansiyel bariyer yaratir Bu olay M x in x e bagli cok karmasik durumlarda oldugu matematikte bazi ozel durumlar haric fiziksel gercekcilikte karsilik bulamamaktadir Yari klasik metotlarin fizik kitaplarinda oldugu gibi tartisimi diger bolumde verilecektir Tamami ile ve karmasik matematiksel islemler 1965 yilinda Froman tarafindan ortaya cikmistir Fikirleri fizik kitaplarinda anonim degildir fakat duzeltmeleri nicel efektler tasir WKB yaklasimiDalga fonksiyonu ustel bir fonksiyon olarak aciklanir PS x eF x displaystyle Psi x e Phi x where F x F x 2 2mℏ2 V x E displaystyle Phi x Phi x 2 frac 2m hbar 2 left V x E right F x displaystyle Phi x gercek ve hayali olarak iki kisma ayrilmistir F x A x iB x displaystyle Phi x A x iB x A x B x gercek degerli fonksiyonlar icin Ikinci denklemi birinci denklemin icine yerlestirerek ve hayali kismin bolumunu kullanarak A x A x 2 B x 2 2mℏ2 V x E displaystyle A x A x 2 B x 2 frac 2m hbar 2 left V x E right Bu denklemi cozmek icin her iki kisimda yari klasik yaklasimlar yapilarak ℏ displaystyle hbar ustel serisinde genisletilmelidir Denklemden ustel serinin denklemin gercek kismini saglamasi icin en az ℏ 1 displaystyle hbar 1 birinci dercesiyle iyi bir klasik limit icin de Planck sabitinin olabildiginde tuksek bir derceyle baslatilmasi suna izin verir A x 1ℏ k 0 ℏkAk x displaystyle A x frac 1 hbar sum k 0 infty hbar k A k x ve B x 1ℏ k 0 ℏkBk x displaystyle B x frac 1 hbar sum k 0 infty hbar k B k x En dusuk mertebeden terimler ile asagidakiler takip etmekte A0 x 2 B0 x 2 2m V x E displaystyle A 0 x 2 B 0 x 2 2m left V x E right ve A0 x B0 x 0 displaystyle A 0 x B 0 x 0 Bu noktada iki asiri durum hesaba katilabilir Durum 1 Eger faz A0 x 0 displaystyle A 0 x 0 ya kiyasla genlik cok yavassa B0 x 2m E V x displaystyle B 0 x pm sqrt 2m left E V x right dd Klasik hareket icindir Genisleme verimin bir sonraki mertebesi ile tekrar cozumu PS x Cei dx2mℏ2 E V x 82mℏ2 E V x 4 displaystyle Psi x approx C frac e i int dx sqrt frac 2m hbar 2 left E V x right theta sqrt 4 frac 2m hbar 2 left E V x right dd durum 2 Eger genligine kiyasla faz yavas sekilde degisirse B0 x 0 displaystyle B 0 x 0 ve A0 x 2m V x E displaystyle A 0 x pm sqrt 2m left V x E right dd Tunellemeye karsilik gelir Genisleme veriminin bir sonraki mertebesi ile tekrar cozumu PS x C e dx2mℏ2 V x E C e dx2mℏ2 V x E 2mℏ2 V x E 4 displaystyle Psi x approx frac C e int dx sqrt frac 2m hbar 2 left V x E right C e int dx sqrt frac 2m hbar 2 left V x E right sqrt 4 frac 2m hbar 2 left V x E right dd Iki durumda da paydalardan gorulmektedir ki iki yaklasik cozumlerde klasik donum noktasi E V x e yakindir Potansiyel tepeden uzakta parcacik serbest ve salinim yapan dalgaya benzer davranir potansiyel tepenin altinda parcacik genlik icinde ustel degisikliklere gider Bu limitlerde parcacigin davranislarini hesaba katarak ve klasik donus noktalarini hesaba katarak genel bir cozum yapilabilir Baslangic icin klasik donus noktasi x1 displaystyle x 1 secilir 2mℏ2 V x E displaystyle frac 2m hbar 2 left V x E right serisinin icinde genisletilir x1 displaystyle x 1 2mℏ2 V x E v1 x x1 v2 x x1 2 displaystyle frac 2m hbar 2 left V x E right v 1 x x 1 v 2 x x 1 2 cdots Birinci dereceden terim tutulmasi dogrusallik saglar 2mℏ2 V x E v1 x x1 displaystyle frac 2m hbar 2 left V x E right v 1 x x 1 Bu yaklasim kullanilarak x1 displaystyle x 1 denklemi diferensiyel denklem olur d2dx2PS x v1 x x1 PS x displaystyle frac d 2 dx 2 Psi x v 1 x x 1 Psi x Cozum olarak Airy fonksiyon kullanilarak bu denklem cozulebilir PS x CAAi v13 x x1 CBBi v13 x x1 displaystyle Psi x C A Ai left sqrt 3 v 1 x x 1 right C B Bi left sqrt 3 v 1 x x 1 right Bu cozumleri tum klasik donum noktalari icin alarak sinirli cozumlerle baglantili genel bir sonuc elde edilebilir Klasik donum noktasinin bir tarafinda verilen 2 katsayi diger tarafinda verilen 2 katsayi kullanilarak bunlarin birlestirilerek elde edilen sonucuyla karar verilebilir Sonuc olarak Airy fonksiyon cozumu sinusun kosunusun ve ustel fonksiyonun belirli sinirlar icinde asimptotu olur C 8 displaystyle C theta ve C C displaystyle C C aralarindaki iliski C 12Ccos 8 p4 displaystyle C frac 1 2 C cos left theta frac pi 4 right ve C Csin 8 p4 displaystyle C C sin left theta frac pi 4 right Katsayinin bulunmasiyla genel cozum bulunabilir Boylece tek bariyer boyunca tunellenen parcacigin dagitim katsayisi T E e 2 x1x2dx2mℏ2 V x E displaystyle T E e 2 int x 1 x 2 mathrm d x sqrt frac 2m hbar 2 left V x E right x1 x2 displaystyle x 1 x 2 potansiyel bariyer icin 2 klasik donum noktasi Dikdortgen bariyer icin bu aciklama soyle ifadelenmistir T E e 22mℏ V0 E x2 x1 V 0 x2 x1 displaystyle T E e 2 sqrt frac 2m hbar V 0 E x 2 x 1 tilde V 0 x 2 x 1 Konuyla ilgili yayinlarN Froman and P O Froman 1965 JWKB Approximation Contributions to the Theory Amsterdam North Holland Razavy Mohsen 2003 Quantum Theory of Tunneling World Scientific ISBN 981 238 019 1 Griffiths David J 2004 Introduction to Quantum Mechanics 2 2 yayinci Prentice Hall bas ISBN 0 13 805326 X and Skinner D 2010 The Physics of Quantum Mechanics An Introduction 3 3 yayinci Cappella Archive bas ISBN 1 902918 51 7 2002 Introductory Quantum Mechanics Addison Wesley ISBN 0 8053 8714 5 Vilenkin Alexander Vilenkin Alexander Winitzki Serge 2003 Particle creation in a tunneling universe Physical Review D 68 2 s 023520 arXiv gr qc 0210034 2 Bibcode 2003PhRvD 68b3520H doi 10 1103 PhysRevD 68 023520 Dis baglantilarAnimation applications and research linked to tunnel effect and other quantum phenomena25 Mayis 2012 tarihinde Wayback Machine sitesinde Universite Paris Sud Animated illustration of quantum tunnelling 9 Ocak 2015 tarihinde Wayback Machine sitesinde Animated illustration of quantum tunnelling in a RTD device 20 Mart 2015 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State























