Bu maddenin veya maddenin bir bölĂŒmĂŒnĂŒn geliĆebilmesi için alakalı konuda uzman kiĆilere gereksinim duyulmaktadır. (Ocak 2012) |
Bu maddede bulunmasına karĆın yetersizliÄi nedeniyle bazı bilgilerin hangi kaynaktan alındıÄı belirsizdir. (Mart 2022) () |
Kuantum mekaniÄi veya kuantum fiziÄi, atom altı parçacıkları inceleyen bir temel fizik dalıdır. Nicem mekaniÄi veya dalga mekaniÄi adlarıyla da anılır. Kuantum mekaniÄi, molekĂŒllerin, atomların ve bunları meydana getiren elektron, proton, nötron, kuark, gluon gibi parçacıkların özelliklerini açıklamaya çalıĆır. ĂalıĆma alanı, parçacıkların birbirleriyle ve ıĆık, x ıĆını, gama ıĆını gibi elektromanyetik ıĆınımlarla olan etkileĆimlerini de kapsar.

Kuantum mekaniÄinin temelleri 20. yĂŒzyılın ilk yarısında Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie Werner Heisenberg, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Wolfgang Pauli gibi bilim insanlarınca atılmıĆtır. Belirsizlik ilkesi, antimadde, Planck sabiti, kara cisim ıĆınımı, dalga fonksiyonu, kuantum alan kuramı gibi kavram ve ilkeler bu alanda geliĆtirilmiĆ ve klasik fiziÄin sarsılmasına neden olmuĆtur.
Etimoloji
Kuantum, Latince 'quantus' (ne kadar, ne bĂŒyĂŒklĂŒkte) sözcĂŒÄĂŒnden gelir ve kuramın belirli fiziksel nicelikler için kullandıÄı kesikli birimlere gönderme yapar. Mekanik, Latince 'mechanicus' (makinelere ait veya yaratıcı) sözcĂŒÄĂŒnden gelir. TĂŒrkçede quantus (ne kadar, ne denli, kaç) sözcĂŒÄĂŒnĂŒn anlamından yola çıkarak nicem sözcĂŒÄĂŒyle karĆılanmıĆtır.
Tarihçe
Bu maddedeki ĂŒslubun, ansiklopedik bir yazıdan beklenen resmĂź ve ciddi ĂŒsluba uygun olmadıÄı dĂŒĆĂŒnĂŒlmektedir. |
Klasik mekanik, her ne kadar baĆarılı olsa da, 1800'lĂŒ yılların sonlarına doÄru kara cisim ıĆıması, tayf çizgileri, fotoelektrik etki gibi birtakım olayları açıklamada yetersiz kalmıĆtır. Klasik fizik, evreni bir "sĂŒreklilik" olarak modelliyordu; ancak Max Planck bazı deneysel gözlemleri açıklayabilmek adına, 1900'de enerjinin paketçiklerden oluĆtuÄunu; 5 yıl sonra da Albert Einstein ıĆıÄın aynı Ćekilde paketçiklerden oluĆtuÄunu, yani ıĆıÄın da, enerjinin de, sĂŒreksizlik gösterdiÄini buldular. Bilim insanları, her ne kadar bu sĂŒreksizlik varsayımlarını klasik mekanik kuramlarından tĂŒretmek için uÄraĆsa da, bu bir sonuç vermedi. Aynı yıllarda, Ernest Rutherford'un atomun iç yapısı ĂŒzerine yaptıÄı deneyler, bir gerçeÄi daha gĂŒn yĂŒzĂŒne çıkardı: Atom, aslında kĂŒĂ§ĂŒk bir çekirdeÄe sahipti.
Elektronun varlıÄı daha önce 1897 senesinde J. J. Thompson tarafından ispat edilmiĆti. Bu durumda, eÄer negatif yĂŒklĂŒ elektronlar pozitif çekirdeÄin etrafında dairesel hareket yapıyorlarsa, klasik fiziÄe göre, çok kısa bir zaman diliminde enerji kaybederek çekirdeÄe dĂŒĆmeleri beklenirdi. Bunun sebebini elektromanyetik teori Ćöyle açıklamaktadır: Ä°vmelenen yĂŒkler ıĆıma yapar, dairesel hareket de (ivmeli) bir hareket olduÄundan, elektron bu ıĆımayla enerji kaybeder ve çekirdeÄe dĂŒĆer; sonuçta, gĂŒneĆ sistemine benzeyen klasik model çöker.
Geçici bir çözĂŒm Niels Bohrâdan gelmiĆtir: "Elektronlar belli kuantizasyon kurallarınca, belli yörĂŒngelerde hareket ederler, enerjileri belli bir deÄere ulaĆmadıkça ıĆıma yapamazlar; bu sayede sistem dengede durabilir." Bu geçici çözĂŒm Hidrojen gibi kĂŒĂ§ĂŒk elementlerde iĆe yaramakta; fakat daha bĂŒyĂŒk kĂŒtleli elementlerde iĆe yaramamaktadır. Bohr atom modeli'nin deneyler ile uyumlu hale gelmesi için modelde birçok dĂŒzenleme yapılmıĆtır. Ancak, Bohr'un atom modeli 1920'lere gelindiÄinde artık iĆ görmemekte, deneylerde gözlenen tayf çizgilerinin yoÄunluÄunu yanlÄ±Ć vermekte, çok elektronlu atomlarda salınım ve emilim dalga boylarını tahmin etmede baĆarısız olmakta, atomik sistemlerin zamana baÄlı hareket denklemini verememekte ve birkaç konuda daha deneysel gerçeklere uymamaktaydı.
Kuantum mekaniÄinin önemli geliĆtiricilerinden biri de, Fransız fizikçi De Broglie'dir.Louis de Broglie; birçok elçi, bakan ve DĂŒk yetiĆtirmiĆ, aristokrat bir Fransız ailesinin çocuÄuydu. Tarih eÄitimi gördĂŒkten sonra fiziÄe geçmiĆ ve 1923'te verdiÄi doktora tezinde, ıĆıÄın hem dalga hem de parçacık karakteri olmasından esinlenerek, aslında bĂŒtĂŒn madde çeĆitlerinin aynı özelliÄi gösterebileceÄini önermiĆtir. Ortaya koyduÄu fikir, Bohr'un "gizemli" yörĂŒngelerini açıklamada baĆarılı oluyordu.
IĆıÄın giriĆim ve kırınım yaptıÄı, yani dalga özelliÄi gösterdiÄi, Thomas Young'ın yaptıÄı çift yarık deneyi ile gösterilmiĆti. Ancak tĂŒm madde parçacıklarının, su dalgaları ile aynı matematiksel özellikleri gösterebileceÄi beklenmiyordu.
Max Planck 1900 yılında kara cisim ıĆınımı problemini ( diye de anılır), çözmek için :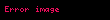
Buna göre, serbest bir parçacık, yönĂŒ k, konumu x, frekansı f ve zaman baÄlılıÄı t olan bir dalga ile ifade edilirse, 2*Ï*(k*x - f*t) , ve bu faz Lorentz dönĂŒĆĂŒmlerinde sabit kalacaksa, k vektörĂŒ ve f frekansı, x vektörĂŒ ve t zamanı gibi dönĂŒĆmelilerdi. DiÄer bir deyiĆle, p ve E gibi. Bunun mĂŒmkĂŒn olabilmesi için, k ve f, p ve E ile aynı baÄımlılıÄa sahip olmalılardı, bu yĂŒzden de onlarla doÄru orantılı olmalılardı.
Bu Ćekilde, fotonlar için E=h*f olduÄundan, madde için de,
varsayımlarını yapmak 'doÄal' gözĂŒkmĂŒĆtĂŒr.
Bu varsayıma ek olarak, de Broglie, herhangi bir kapalı yörĂŒngenin 1/|k| nın tam katı olması varsayımını da kullanarak, deneysel olarak gözlenen ve Arnold Sommerfeld ve Bohr tarafından "kuantize olma Ćartları" olarak anılan Ćartları, matematiksel olarak kolayca tĂŒretti. Bu tĂŒretme gayet gizemli bir Ćekilde doÄru sonuçlar verince (Davisson ve Germer, 1927 yılında Bell Laboratuvarlarında gerçekleĆtirdikleri deneyle, elektronların da aynı ıĆık gibi giriĆim yaptıÄını ortaya koydular. Deney 1924'te de Brogli tarafından önerilmiĆti) insanlar deneysel olarak baĆka Ćeyleri tahmin etmesini de beklediler.
Elbette yanıldılar Ă§ĂŒnkĂŒ bu Ćartlar serbest ıĆık parçaları için oluĆturulan varsayımların, çekirdeÄe baÄlı elektronlar için uyarlanmasıydı ve çok ileri götĂŒrĂŒlmemesi gerekiyordu.
Ama dalga mekaniÄi için doÄru çıkÄ±Ć noktası idi.
Enteresan bir Ćekilde, 1925-1926 yılları arasında Werner Heisenberg, Max Born, Wolfgang Pauli ve Pascual Jordan, matris mekaniÄi ile kuantum mekaniÄinin formal tanımını yaptılar. Ama formalizmlerinde dalga mekaniÄine yer vermediler. Benimsedikleri felsefe ise, tamamen pozitivist idi. Yani sadece deneysel olarak gözlenebilen deÄerleri göz önĂŒne alan bir yaklaĆım kullandılar.
1926 yılında Erwin Schrödinger bir dizi denklemle dalga mekaniÄini yeniden canlandırdı. Sonunda kendi dalga mekaniÄinden Heisenberg'in matriks mekaniÄini de tĂŒretip iki formalizmin matematiksel olarak denk olduÄunu da gösterdi (son makalelerinden birinde Schrödinger, relativistik bir dalga denklemi de sunar).
Dirac'a göre ise tarih biraz daha farklı iĆlemiĆtir. Ona göre, Schrödinger önce relativistik dalga denklemini geliĆtirdi, sonra bunu kullanarak hidrojenin spektrumunu hesapladı ve deneylere uymadıÄını gördĂŒ. Ancak bu denklemin, dĂŒĆĂŒk hızlarda geçerli olan versiyonu aslında çalıĆıyordu ve bildiÄimiz Schrodinger dalga denklemine ulaĆılıyordu.
Daha sonra relativistik dalga denklemi Oskar Klein ve Walter Gordon tarafından yayınladı ve hùlù Klein-Gordon denklemi olarak anılır.
Bu noktadan sonra Dirac; teoriyi özel görelilikle uyumlu hale getirmiĆ ve bazı deneylerin sonuçlarını teorik olarak ĂŒretmiĆtir. ĂrneÄin pozitron'un varlıÄını 1932 senesinde Carl David Anderson kanıtlamıĆtır ve nobel ile ödĂŒllendirilmiĆtir. Kuantum teorisi, daha sonra 1940'larda Sin-Itiro Tomonaga, Julian Schwinger ve Richard P. Feynman'ın kuantum elektrodinamiÄi konusunda önemli çalıĆmalarıyla geliĆimine devam etmiĆtir. 1950'li ve 60'lı yıllar ise Kuantum renk dinamiÄinin geliĆimine tanık olmuĆtur.
GeliĆmeler
- 1897: Pieter Zeeman, ıĆıÄın bir atom içindeki yĂŒklĂŒ parçacıkların hareketi sonucu yayımlandıÄını buldu; J.J. Thomson da, elektronu keĆfetti.
- 1900: Max Planck, kara cisim ıĆımasını kuantumlanmÄ±Ć enerji yayımı ile açıkladı, kuantum kuramı böylece doÄmuĆ oldu.
- 1905: Albert Einstein dalga özellikleri olan ıĆıÄın aynı zamanda, daha sonra foton diye adlandırılacak olan, belirli bĂŒyĂŒklĂŒkte enerji paketlerinden oluĆtuÄu dĂŒĆĂŒncesini ortaya attı.
- 1911-1913: Ernest Rutherford, atomun çekirdek modelini oluĆturdu. Bohr ise atomu bir gezegen sistemi gibi betimledi.
- 1923: Arthur Compton, X - ıĆınlarının elektronlarla etkileĆimlerinde minyatĂŒr bilardo topları gibi davrandıklarını gözlemledi. Böylece ıĆıÄın parçacık davranıĆı hakkında yeni kanıtlar ortaya koydu.
- 1923: Louis de Broglie, dalga-parçacık ikiliÄini genelleĆtirdi.
- 1924: Satyendra Nath Bose-Albert Einstein, kuantum parçacıklarını saymak için, diye adlandırılan yeni bir yöntem buldular.
Klasik mekanik, kuantum mekaniÄi ve kuantum mekaniÄinin matematiÄi
Klasik mekanik, nesnelerin konum ve momentumları bilgilerini kullanarak, çeĆitli kuvvet alanları altında nasıl hareket etmeleri gerektiÄini bulmaya çalıĆır. Kökleri çok eskiye dayansa da baĆlangıcının Newton'un Principia'sı olduÄunu kabul etmek yanlÄ±Ć olmaz. Daha sonra Euler, Lagrange, Jacobi, Hamilton, Poisson, Maxwell, Boltzman (Ä°statiksel mekanik ve klasik elektromanyetik teori de klasik mekaniÄe katılabilir) gibi birçok ad tarafından çok çeĆitli bakÄ±Ć açıları geliĆtirilmiĆ ve birçok alanda baĆarılı bir Ćekilde uygulanmıĆtır. Klasik mekaniÄin tamamlanmasının Einstein'ın görelilik kuramları ile gerçekleĆtiÄini söylemek yanlÄ±Ć olur. Klasik mekanik çok baĆarılı olmasına karĆın, 1800'lĂŒ yılların sonlarına doÄru, siyah cisim ıĆıması, tayf çizgileri, fotoelelektrik etki gibi birtakım olayları açıklamada yetersiz kalmıĆtır. Açıklamaların yanlıĆlıÄı bilim adamlarının yetersizliÄinden deÄil aksine klasik mekaniÄin yetersizliÄinden kaynaklanıyordu. Klasik mekanikteki sorunun ne olduÄunu anlatmak aĆırı teknik kaçacaktır, ancak en yalın halde klasik mekanik, evreni sĂŒrekli olarak modeller ve bu yaklaĆım kendi içinde tutarlı deÄildir. Bunu görmek için termodinamikteki eĆ-daÄılım prensibine ("Ä°ngilizce: equipartition theorem") bakmalıyız. Ăç konum (x, y, z) ve ĂŒĂ§ momentumla (px, py, pz) tanımlanan parçacıklar, sonsuz sayıda parametreyle tanımlanan alanlarla bir aradadır. EĆ-daÄılım kuramınca sistemin enerjisinin, denge durumunda, sistemin tĂŒm bileĆenlerine eĆit biçimde daÄılması gerekir. Alanlar sonsuz bileĆene sahip olduÄundan bĂŒtĂŒn enerji alanlara daÄılmalıdır. (Daha teknik bir ifade ile, denge durumundaki sistemde enerji, bĂŒtĂŒn özgĂŒrlĂŒk derecelerine eĆ olarak daÄılır, alanlar sonsuz özgĂŒrlĂŒk derecesine sahip olduÄu için bĂŒtĂŒn enerji alanlara akmalıdır.) Evren dengede varsayılırsa, deneysel olarak böyle bir gözlemin olmaması, klasik mekaniÄin "sĂŒreklilik" paradigmasında bir soruna iĆaret eder.
Kuantum kuramı ise olayı bambaĆka bir Ćekilde ele alır. Parçacıklar artık doÄrudan 3 konum ve 3 momentumla tanımlanmak yerine bir "dalga fonksiyonu" ile tanımlanırlar. Bu dalga fonksiyonu parçacıÄın bĂŒtĂŒn bilgisini içinde barındırır ve dalga fonksiyonuna uygun "sorular" sorularak gerekli bilgi alınır. ĂrneÄin konum bilgisi için dalga fonksiyonuna "Parçacık nerede?" sorusunu sorarsınız, o ise size parçacıÄın soruyu sorduÄunuz anda nerede olabileceÄini söyler. Buradaki kritik nokta olabilirliktir. Bu, dalga fonksiyonunun bir de "olasılık fonksiyonu" olarak anılmasına neden olmaktadır. Daha sonra, bu olasılıksal durumu bilinçli olup olmama durumuna baÄlayan Kopenhag Yorumu ortaya atılmıĆtır. (Matematik altyapısı yetersiz olanlar denklemleri görmezden gelebilirler.) Matematiksel olarak olayı Ćöyle tanımlayabiliriz:
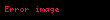
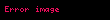
integrali bize x'in beklenen deÄerini verir. Yukarıda bahsedilen soru sorma iĆlemi tam olarak böyle yapılır. Benzer Ćekilde momentumun beklenen deÄeri için; 
Ćeklinde soruyu sorarız. 
Konum ve momentum dıĆında daha birçok gözlemlenebilir ile iĆlem yapılabilir. Ancak konum ve momentum operatörleri kullanılarak diÄer birçok operatörĂŒ elde etmek mĂŒmkĂŒndĂŒr. Ä°Ćin ilginç yanı bu operatörle elde etmek için klasik formĂŒller kullanılır. ĂrneÄin kinetik enerji klasik mekanikte;
Ćeklinde tanımlanırken kuantum fiziÄinde kinetik enerji operatörĂŒ yine aynı ifadeyle yazılır. Tek fark "p" artık bir sayı deÄil bir operatördĂŒr. Bu bize Ehrenfest teoremince saÄlanır ve bĂŒtĂŒn operatörleri klasik yasaları kullanarak tĂŒretebiliriz. Bu noktada "Peki, dalga fonksiyonu nedir?" sorusuna dönmeliyiz. Dalga fonksiyonu bize Schrödinger denklemi tarafından verilen, bir bakıma parçacıÄın kimlik kartıdır. Bir boyutta Schrödinger denklemi;
Ćeklinde yazılabilir. Ä°fade bir bakıma enerji denklemidir ve bahsi geçen "kimlik" kartını sistemin enerjisine göre verir. (Burada kimlikten kasıt, parçacıÄın elektron mu yoksa nötron mu olduÄu deÄil, momentumu, konumu, kinetik enerjisi gibi gözlemlenebilir olmalarıdır.) Bu denklem çözĂŒldĂŒÄĂŒnde parçacıÄımızın dalga fonksiyonunu elde etmiĆ oluruz. En basit atom olan hidrojen atomunun zamandan baÄımsız analitik olarak çözĂŒlmesi bile zordur, neyse ki belli formalizmlerle, daha karmaĆık sistemleri yaklaĆımlar yaparak çözmek mĂŒmkĂŒn oluyor.
Kuantum mekaniÄi temelinde bir olasılık teorisidir. Dalga fonksiyonu içinde sistemin bĂŒtĂŒn olası durumlarını barındırır. Siz soruyu sorduÄunuzda size en olası cevabı verir, ancak soru sorma iĆlemi dalga fonksiyonunu "daÄıtır" ve siz bir daha sorduÄunuz zaman artık baĆka bir cevap alırsınız. Bunun yanı sıra kuantum mekaniÄi yapısı ötĂŒrĂŒ belirsizlikler barındırır. Bu belirsizlikler bazı gözlemlenebilir olanı ne kadar iyi bilirseniz diÄer bazıları hakkında o kadar az Ćey bileceÄinizi söyler. ĂrneÄin konum ve momentum böyle bir çift oluĆturur. Birini ne kadar iyi bilirseniz diÄeri hakkında o kadar az bilginiz olur. Bu Heisenberg belirsizlik ilkesi olarak bilinir. Konum ve momentum için Heisenberg belirsizlik ilkesi Ćöyle gösterilir:
Bu ifade de 

Yukarıda ele alınan kuantum mekaniÄi, öklidyen bir uzayda çalıĆılmÄ±Ć kuantum mekaniÄidir, diÄer bir deyiĆle göreceli deÄildir. Einstein'ın özel görelilik kuramına uyan bir kuantum mekaniÄi tĂŒretmek mĂŒmkĂŒndĂŒr. Hatta ilk bakıĆta kolay bir uÄraĆtır. Kuantum fikrine ve özel göreliliÄe biraz aĆina olan biri bile çözĂŒme kolayca ulaĆır. Yukarıda deÄinilen Schrödinger denklemini daha sade bir formda Ćöyle ele alabiliriz:
Burada H olarak verilen Hamiltonian operatörĂŒdĂŒr. (Toplam enerji olarak dĂŒĆĂŒnĂŒlebilir.) Relativistik olmayan serbest parçacık (potansiyel enerji sıfır) için Hamiltonian:
olarak verilir. Relativistik serbest parçacık içinse Hamiltonian:
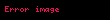
Ćeklinde yazılabilir. Ä°fade pek yabancı deÄil, deÄil mi? Hayır, olaya klĂąsik mekanik açısından bakarsanız, parçacıÄın durduÄunu kabul edersek, momentum sıfır olacak ve ĂŒnlĂŒ 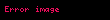

Karesi alınırsa
elde edilir. Bu denklem Klein-Gordon denklemi olarak bilinir. Ancak denklem birtakım teknik nedenden ötĂŒrĂŒ sorunludur. Daha geçerli relativistik çözĂŒm Dirac tarafından keĆfedilmiĆtir ve kendi adıyla anılan denklemle verilir. Ultramikroskobik boyutlarda (Planck UzunluÄu) uzayın kĂŒĂ§ĂŒk dalga boylarında bir kaos olduÄu dĂŒĆĂŒnĂŒlĂŒr. Evrenin milyarda birinin milyarda birinin milyonda biri boyutlarda gözleyecek olursanız evren bir kaos olarak görĂŒnĂŒr.
Kuantum mekaniÄi tarihi geliĆimi boyunca birçok sınavdan alnının akıyla çıkmayı baĆarmıĆtır. Olguları bĂŒyĂŒk bir doÄrulukla açıklaması, yeni olgulara ıĆık tutması bir teoriden beklenen özelliklerdir ve kuantum mekaniÄi bu iĆi gerçekten oldukça iyi baĆarmıĆtır. Kuantum fikirleri ĂŒzerine geliĆen kuantum elektrodinamiÄi (QED) ve kuantum renk dinamiÄi (QCD) bu gĂŒne kadarki hiçbir teorinin ulaĆamadıÄı hassasiyetlerde sonuçlar vermiĆlerdir. Ne var ki geçtiÄimiz yĂŒzyılın çok bĂŒyĂŒk iki teorik açılımı bir biriyle uyuĆmamaktadır. DoÄada bilinen 4 kuvvetten 3'ĂŒ, elektromanyetizma, zayıf ve gĂŒĂ§lĂŒ kuvvetler, kuantum kuramlarıyla ele alınabilirken kĂŒtleçekimin henĂŒz tutarlı bir kuantum kuramı bulunamamıĆtır. Her ne kadar sicim kuramları kuantum kĂŒtleçekime aday gibi görĂŒnse de çözĂŒlmesi gereken çok bĂŒyĂŒk sorunlar hĂąlen bulunmaktadır. GĂŒnĂŒmĂŒzde yaygın kanı kuantum ve kĂŒtleçekimin ĂŒstĂŒnde, doÄrusal olmayan daha genel bir kuramın yer aldıÄıdır.
Kuantum mekaniÄinin uygulamaları
Kimyasal ve fizik bilimlerinin temelleri Ću temel araĆtırma alanları ĂŒstĂŒne kuruludur:
- AkıĆkanlar MekaniÄi
- Elektromanyetik
- Ä°statistiksel Mekanik
- Kimyasal Kinetik
- KlĂąsik Mekanik
- Kuantum MekaniÄi
- Optik
- Termodinamik
DiÄer tĂŒm fizik ve kimya dalları, bu temel dĂŒzeneklerin uygulamalarıdır. O halde bunlara "saf", diÄerlerine "uygulamalı" fizik ve kimya gözĂŒ ile bakılabilir. Kuantum mekaniÄinin mikro sistemlere uygulanması ile Ću uygulamalı fizik ve kimya dalları tĂŒretilmiĆtir:
- Anorganik Kimya, Organik Kimya, Biyokimya: Bunlar da temel uygulama dalı olan Kuantum Kimyası'nın özel olarak -sırasıyla- anorganik, organik ve biyomolekĂŒllere olan uygulamasıdır.
- Katı Hal Kimyası (FiziÄi): Katı halin kuantum mekaniÄi
- Kuantum Kimyası: Atom ve molekĂŒllerin kuantum mekaniÄi (Fizik'te genelde Atom ve MolekĂŒl FiziÄi ismi tercih edilir)
- NĂŒkleer Kimya (Fizik): ĂekirdeÄin kuantum mekaniÄi
- Parçacık Kimyası (FiziÄi): Atomaltı parçacıkların kuantum mekaniÄi
- Plazma Kimyası (FiziÄi): Plazmanın kuantum mekaniÄi
- Sıvı Hal Kimyası (FiziÄi): Sıvı halin kuantum mekaniÄi
Fotokimya ve fotofizik, yĂŒzey kimyası vb. pek çok dal da kuantum mekaniÄinden uygulamalar içermektedir.
Kuantum mekaniÄi her ne kadar çok kĂŒĂ§ĂŒklerin dĂŒnyasını modelleyen bir kuram olsa da uygulama alanları gerek dolaysız gerek dolaylı yollarla çok geniĆtir. Kuantum mekaniÄi biyoloji, malzeme bilimi, elektronik gibi birçok alanın gĂŒnĂŒmĂŒzdeki anlamına kavuĆmasını saÄlamıĆtır.
Laser, maser, yarı iletkenler gibi gĂŒnĂŒmĂŒzĂŒn olmazsa olmazlarının icatları, kuantum mekaniÄi sayesinde mĂŒmkĂŒn olmuĆtur. Ayrıca elektron mikroskobu, atomik kuvvet mikroskobu, taramalı tĂŒnellemeli mikroskop gibi biyoloji ve nanoteknolojik uygulamaların olmazsa olmazları; PET-Scan (Positron Emmission Tomography), MRI (Magnetic Resonance Imaging), Tomografi gibi tıbbi görĂŒntĂŒleme cihazları yine kuantum mekaniÄinin bize gösterdiÄi belli doÄa olgularını kullanarak çalıĆırlar. Yine tıp, nanoteknoloji, elektronik gibi birçok alanda sayısız kullanımı olan fiberler kuantum mekaniÄinin doÄrudan uygulamasına örnektir. Modern kimya, kuantum fikirleri ĂŒzerine inĆa edilmiĆ ve çok karmaĆık molekĂŒllerin yapıları bu sayede anlaĆılmıĆtır.
Kuantum mekaniÄi felsefesi
Kuantum mekaniÄi bugĂŒne kadar girdiÄi tĂŒm sınavlardan baĆarıyla çıkmıĆtır. Peki, nasıl olur da bu denli baĆarılı bir teorinin eleĆtirel bir felsefesinden söz edilebilir? Dahası teorinin bazı felsefi sorular ortaya çıkardıÄını nasıl ileri sĂŒrebiliriz?
Kuantum mekaniÄi net ve saÄlam matematik temeller ĂŒzerine kurulmuĆtur. Sistemlerin doÄası bu matematikle modellenir. Ancak baĆlı baĆına bu modelleme kuantum mekaniÄinin temel kavramlarının çözĂŒmlenmesinde felsefecilere göre yetersizdir. Ărnek verecek olursak, 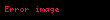
Fizikçiler arasında genel yaklaĆım, felsefe yapmak yerine deÄiĆik koĆullar altında Schrödinger denklemini çözmek ve teorik olarak bulunan sonuçları deneysel sonuçlar ile karĆılaĆtırmaktır. Ćimdiye kadar deneyler bu Ćekilde hep baĆarı ile açıklanabilmiĆtir, yani doÄa, kuantum mekaniÄinin tahminlerine göre hareket etmektedir. Burada ĂŒzerinde durulabilecek bir nokta, kuantum fiziÄinin, ĂŒzerinde deney yapılması imkansız kavramların felsefesini yapmaya gerek duymaması, bunun yerine sadece deney ve teorinin uyumuna bakmasıdır.
Kuantum mekaniÄi tamamlanmÄ±Ć bir teori midir?
Kuantum mekaniÄinin temelleri Heisenberg belirsizlik ilkesinin formĂŒle edildiÄi 1927 yılından bu zamana dek hiçbir deÄiĆikliÄe uÄramamıĆtır. Kuantum mekaniÄinin uzantısı olarak ortaya çıkan teorilerde ortaya çıkan kavramlar da, bildiÄimiz kadarıyla bu temel ilkelerde deÄiĆiklik yapılmasını gerektirmezler. Kuantum mekaniÄi doÄduÄu andan itibaren temel ilkelerin anlaĆılması bakımından bĂŒyĂŒk tartıĆmalara yol açmıĆtır. Bu tartıĆmalardan biri A. Einstein, B. Podolsky ve N. Rosen'in 1935 yılında "DoÄanın Kuantum Mekaniksel Tasviri TamamlanmÄ±Ć Kabul Edilebilir mi?" baĆlıÄıyla yayınladıkları ve yazarlarının adlarının baĆ harfleriyle "EPR Paradoksu" olarak adlandırılan makalesiyle baĆlamÄ±Ć olup, hĂąlen de önemini korumaktadır. EPR makalesi bir fizik teorisinin tamamlanmÄ±Ć kabul edilebilmesi için iki temel koĆulu yerine getirmesi gerektiÄini söyler. Bunlar;
- Teorinin doÄruluÄu
- Teorinin tamamlanmıĆlıÄı
EPR makalesine göre teorinin doÄru olarak nitelendirilebilmesi için teorinin deney sonuçlarıyla uyumluluÄu göz önĂŒne alınmalıdır. Bu bakımdan kuantum mekaniÄi deneylerle bĂŒyĂŒk bir uyum gösterdiÄi için doÄru kabul edilir. Teorinin baĆarısı için gerekli olan diÄer koĆul olan tamamlanmıĆlık için ise makalede Ću koĆul verilmiĆtir: "Bir fizik kuramında, her fiziksel gerçekliÄe karĆılık olan bir öge bulunmalıdır."
Makalede fiziksel gerçeklik Ću Ćekilde tanımlanmıĆtır: "Bir fiziksel niceliÄin deÄerini, dinamik sistemi herhangi bir biçimde bozmaksızın kesinlikle tahmin edebiliyorsak, o zaman, fiziksel gerçekliÄin, bu fiziksel niceliÄe karĆılık olan bir ögesi vardır."
Fiziksel niceliÄin kesin bir deÄerini, dinamik sistemi bozmadan teoride elde edebiliyorsak, o zaman, teoriden hesap ile elde edilen bu kesin deÄer fiziksel gerçekliÄin bir ögesine karĆılık gelecektir. Ancak fiziksel gerçekliÄin bĂŒtĂŒn ögelerinin fizik teorisinde karĆılıklarının bulunması gerektiÄine dair bir koĆul ileri sĂŒrĂŒlmemiĆtir. Bu nedenle, EPR'ye göre, doÄru olan teorinin aynı zamanda tamamlanmÄ±Ć olması gerekmez.
Fiziksel gerçeklik ölĂ§ĂŒtĂŒnĂŒn kuantum mekaniÄi çerçevesinde nasıl kullanıldıÄı makalede Ću örnekle açıklanmıĆtır. Elimizdeki parçacık 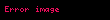
Ćeklinde gösterelim. Bu parçacıÄın momentumu ölĂ§ĂŒlmeden önce Ću önerme ileri sĂŒrĂŒlebilir: ParçacıÄın momentumunun ölĂ§ĂŒmden sonra 
olduÄunu kabul edelim. EÄer alınabilecek birden çok momentum deÄeri mevcutsa 
Kitap
Ders kitapları
- J. J. Sakurai, J. Napolitano, Modern Kuantum MekaniÄi, Palme Yayıncılık 2012 ().
- T. Dereli, Kuantum MekaniÄi I, ODTĂ Yayıncılık ().
- E. AygĂŒn, M. Zengin, Kuantum FiziÄi, Ankara Ăniversitesi Yayınları, 2. baskı, 1992.
- J. J. Sakurai, Advanced Quantum Mechanics, Addison-Wesley, 1967().
- E. RızaoÄlu, M. Yalçınkaya, Ă. GĂŒltekin, Alfa Yayınları, 2021 ().
FiziÄin diÄer alanları hakkında yazılan ilgili ders kitapları
- B. H. Bransden, C. J. Joachain, Atom ve MolekĂŒl FiziÄi, On Dokuz Mayıs Ăniversitesi Yayınları.
- T. N. Durlu, Katı Hal FiziÄine GiriĆ, Ankara Ăniversitesi Yayınları, 2. baskı, 1992.
- E. AygĂŒn, M. Zengin, Atom ve MolekĂŒl FiziÄi, Ankara Ăniversitesi Yayınları, 1992.
- D. Halliday, R. Resnick, FiziÄin Temelleri 2, Palme Yayıncılık.
- A. Beiser, ĂaÄdaĆ FiziÄin Kavramları, Dicle Ăniversitesi Yayınları, 2. baskı,1989.
- C. Ănem, Fizikte Matematik Metotlar, Birsen Yayıncılık, 3. baskı.
Kaynakça
- Ăzel
- ^ Ăaykara, Emine (1964); Oktay SinanoÄlu Kitabı / TĂŒrk AynĆtaynı, TĂŒrkiye Ä°Ć Bankası KĂŒltĂŒr Yayınları, s. 178. ISBN, 9754582947
- ^ Nihat TaĆpınar, Dalga mekaniÄi: stokes 3. mertebe dalga teorisi ve tabloları. Dokuz EylĂŒl Ăniversitesi, (1987) - 291 sayfa.
- ^ a b "Quantum mechanics." 11 Temmuz 2014 tarihinde Wayback Machine sitesinde . Britannica.com. 10 AÄustos 2014.
- ^ "quantum." 12 AÄustos 2014 tarihinde Wayback Machine sitesinde . Online Etymology Dictionary. 10 AÄustos 2014.
- ^ "mechanics." Oxford Dictionary of English 2e, Oxford University Press, 2003.
- ^ "Otomatik Ăizgi Tanımı Programı" (PDF). T. C. Ä°stanbul Ăniversitesi Fen Bilimleri EnstitĂŒsĂŒ. 27 Mart 2021 tarihinde kaynaÄından (PDF). EriĆim tarihi: 20 Ćubat 2021.
- ^ a b (PDF). 11 Ocak 2020 tarihinde kaynaÄından (PDF) arĆivlendi.
- ^ . Britannica. 19 Haziran 2015 tarihinde kaynaÄından arĆivlendi.
- ^ J.J. Thompson And The Discovery Of The Electron, E. A. Davis,Isabel Falconer
- ^ (PDF). Dr. A. KĂŒrĆad Poyraz. F. Ă. Tıp FakĂŒltesi Radyoloji A. D. 28 EylĂŒl 2020 tarihinde kaynaÄından (PDF) arĆivlendi.
- ^ "Elektro Manyetik Teori" (PDF). O. Ăakır (AU). XII. Ulusal Parçacık Hızlandırıcıları ve Dedektörleri Yaz Okulu, HTE GölbaĆı, 2-7 Temmuz 2018. 27 Mart 2021 tarihinde kaynaÄından (PDF). EriĆim tarihi: 20 Ćubat 2021.
- ^ "Elektro Manyetik Alan Teorisi" (PDF). Yardımcı Doktor Doçent Aslan Ănal'ın not defteri. Yardımcı Doktor Doçent Aslan Ănal. 27 Mart 2021 tarihinde kaynaÄından (PDF). EriĆim tarihi: 20 Ćubat 2021.
- ^ a b c . Niels Bohr'un biyografisi. Britannica. 7 Temmuz 2015 tarihinde kaynaÄından arĆivlendi.
- ^ "KUANTUM AYAR ALAN TEORÄ°LERÄ°NÄ°N KUANTÄ°ZASYONU VE STANDART MODEL" (PDF). PROF. DR. MĂGE BOZ EVÄ°NAY?. Hacettepe Ăniversitesi. 2015. 27 Mart 2021 tarihinde kaynaÄından (PDF). EriĆim tarihi: 20 Ćubat 2021.
- ^ a b ""Bohr'un Atom modellerinin yetersizlikleri"". Psiko-fizik. 7 Mayıs 2021 tarihinde kaynaÄından . EriĆim tarihi: 20 Ćubat 2021.
- ^ . Britannica. 7 Temmuz 2015 tarihinde kaynaÄından arĆivlendi.
- ^ a b c . Louis de Broglie'nin Biyografisi çalıĆması. Britannica. 7 Temmuz 2015 tarihinde kaynaÄından arĆivlendi.
- ^ Elizabeth H. Oakes, Encyclopedia of World Scientists Facts on File Science Library, (2007) s.19. ISBN 13:9780816061587
- Genel
- Kuantum FiziÄi (1/2)27 EylĂŒl 2007 tarihinde Wayback Machine sitesinde .
- Kuantum FiziÄi (2/2)27 EylĂŒl 2007 tarihinde Wayback Machine sitesinde .
Ayrıca bakınız
DÄ±Ć baÄlantılar
- CERN26 Temmuz 2007 tarihinde Wayback Machine sitesinde .
- Kuantum Teorisi ve Atomaltı Parçacıklar 9 Mayıs 2018 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kĂŒtĂŒphane, kĂŒtĂŒbhane, ara, ara bul, bul, herĆey, ne arasanız burada,hikayeler, makale, kitaplar, öÄren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, tĂŒrk, tĂŒrkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ĂŒcretsiz, ĂŒcretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, mĂŒzik, Ćarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddenin veya maddenin bir bolumunun gelisebilmesi icin alakali konuda uzman kisilere gereksinim duyulmaktadir Ayrintilar icin lutfen tartisma sayfasini inceleyin veya yeni bir tartisma baslatin Konu hakkinda uzman birini bulmaya yardimci olarak ya da maddeye gerekli bilgileri ekleyerek Vikipedi ye katkida bulunabilirsiniz Ocak 2012 Bu maddede kaynak listesi bulunmasina karsin metin ici kaynaklarin yetersizligi nedeniyle bazi bilgilerin hangi kaynaktan alindigi belirsizdir Lutfen kaynaklari uygun bicimde metin icine yerlestirerek maddenin gelistirilmesine yardimci olun Mart 2022 Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin Kuantum mekanigi veya kuantum fizigi atom alti parcaciklari inceleyen bir temel fizik dalidir Nicem mekanigi veya dalga mekanigi adlariyla da anilir Kuantum mekanigi molekullerin atomlarin ve bunlari meydana getiren elektron proton notron kuark gluon gibi parcaciklarin ozelliklerini aciklamaya calisir Calisma alani parcaciklarin birbirleriyle ve isik x isini gama isini gibi elektromanyetik isinimlarla olan etkilesimlerini de kapsar Belirli enerji seviyelerinde asagiya dogru artarak n 1 2 3 ve acisal momentum lardaki saga dogru artarak s p d bir hidrojen atomu elektronunun dalga fonksiyonlari Daha parlak olan bolgeler elektronun pozisyonu icin daha yuksek olasilik genligine isaret ediyor Kuantum mekaniginin temelleri 20 yuzyilin ilk yarisinda Max Planck Albert Einstein Niels Bohr Louis de Broglie Werner Heisenberg Erwin Schrodinger Max Born John von Neumann Paul Dirac Wolfgang Pauli gibi bilim insanlarinca atilmistir Belirsizlik ilkesi antimadde Planck sabiti kara cisim isinimi dalga fonksiyonu kuantum alan kurami gibi kavram ve ilkeler bu alanda gelistirilmis ve klasik fizigin sarsilmasina neden olmustur EtimolojiKuantum Latince quantus ne kadar ne buyuklukte sozcugunden gelir ve kuramin belirli fiziksel nicelikler icin kullandigi kesikli birimlere gonderme yapar Mekanik Latince mechanicus makinelere ait veya yaratici sozcugunden gelir Turkcede quantus ne kadar ne denli kac sozcugunun anlamindan yola cikarak nicem sozcuguyle karsilanmistir TarihceBu maddedeki uslubun ansiklopedik bir yazidan beklenen resmi ve ciddi usluba uygun olmadigi dusunulmektedir Maddeyi gelistirerek ya da konuyla ilgili tartismaya katilarak Vikipedi ye katkida bulunabilirsiniz Klasik mekanik her ne kadar basarili olsa da 1800 lu yillarin sonlarina dogru kara cisim isimasi tayf cizgileri fotoelektrik etki gibi birtakim olaylari aciklamada yetersiz kalmistir Klasik fizik evreni bir sureklilik olarak modelliyordu ancak Max Planck bazi deneysel gozlemleri aciklayabilmek adina 1900 de enerjinin paketciklerden olustugunu 5 yil sonra da Albert Einstein isigin ayni sekilde paketciklerden olustugunu yani isigin da enerjinin de sureksizlik gosterdigini buldular Bilim insanlari her ne kadar bu sureksizlik varsayimlarini klasik mekanik kuramlarindan turetmek icin ugrassa da bu bir sonuc vermedi Ayni yillarda Ernest Rutherford un atomun ic yapisi uzerine yaptigi deneyler bir gercegi daha gun yuzune cikardi Atom aslinda kucuk bir cekirdege sahipti Elektronun varligi daha once 1897 senesinde J J Thompson tarafindan ispat edilmisti Bu durumda eger negatif yuklu elektronlar pozitif cekirdegin etrafinda dairesel hareket yapiyorlarsa klasik fizige gore cok kisa bir zaman diliminde enerji kaybederek cekirdege dusmeleri beklenirdi Bunun sebebini elektromanyetik teori soyle aciklamaktadir Ivmelenen yukler isima yapar dairesel hareket de ivmeli bir hareket oldugundan elektron bu isimayla enerji kaybeder ve cekirdege duser sonucta gunes sistemine benzeyen klasik model coker Gecici bir cozum Niels Bohr dan gelmistir Elektronlar belli kuantizasyon kurallarinca belli yorungelerde hareket ederler enerjileri belli bir degere ulasmadikca isima yapamazlar bu sayede sistem dengede durabilir Bu gecici cozum Hidrojen gibi kucuk elementlerde ise yaramakta fakat daha buyuk kutleli elementlerde ise yaramamaktadir Bohr atom modeli nin deneyler ile uyumlu hale gelmesi icin modelde bircok duzenleme yapilmistir Ancak Bohr un atom modeli 1920 lere gelindiginde artik is gormemekte deneylerde gozlenen tayf cizgilerinin yogunlugunu yanlis vermekte cok elektronlu atomlarda salinim ve emilim dalga boylarini tahmin etmede basarisiz olmakta atomik sistemlerin zamana bagli hareket denklemini verememekte ve birkac konuda daha deneysel gerceklere uymamaktaydi Kuantum mekaniginin onemli gelistiricilerinden biri de Fransiz fizikci De Broglie dir Louis de Broglie bircok elci bakan ve Duk yetistirmis aristokrat bir Fransiz ailesinin cocuguydu Tarih egitimi gordukten sonra fizige gecmis ve 1923 te verdigi doktora tezinde isigin hem dalga hem de parcacik karakteri olmasindan esinlenerek aslinda butun madde cesitlerinin ayni ozelligi gosterebilecegini onermistir Ortaya koydugu fikir Bohr un gizemli yorungelerini aciklamada basarili oluyordu Isigin girisim ve kirinim yaptigi yani dalga ozelligi gosterdigi Thomas Young in yaptigi cift yarik deneyi ile gosterilmisti Ancak tum madde parcaciklarinin su dalgalari ile ayni matematiksel ozellikleri gosterebilecegi beklenmiyordu Max Planck 1900 yilinda kara cisim isinimi problemini diye de anilir cozmek icin E hf displaystyle E hf denklemini kullanmisti Bu denklem foton kavraminin baslangici oldu cunku f frekansindaki elektron salinimindan olusan isigin klasik mekanikle uyusmayan bir sekilde h f nun sadece tam sayi katlarinda kesikli enerjiler E tasiyabilecegini varsaymisti h gunumuzde Planck sabiti adiyla anilir Fotonlar dalga ozelligi gosteriyorsa madde de bu dualiteyi ikiligi gosterebilir analojisi cok kuvvetli bir fikir idi Bunun yaninda onemli bir ipucu da Einstein in birkac yil once ozel gorelilik ispatinda kullandigi Lorentz Donusumleri idi Buna gore serbest bir parcacik yonu k konumu x frekansi f ve zaman bagliligi t olan bir dalga ile ifade edilirse 2 p k x f t ve bu faz Lorentz donusumlerinde sabit kalacaksa k vektoru ve f frekansi x vektoru ve t zamani gibi donusmelilerdi Diger bir deyisle p ve E gibi Bunun mumkun olabilmesi icin k ve f p ve E ile ayni bagimliliga sahip olmalilardi bu yuzden de onlarla dogru orantili olmalilardi Bu sekilde fotonlar icin E h f oldugundan madde icin de E hf ve k p h displaystyle E hf ve k p h varsayimlarini yapmak dogal gozukmustur Bu varsayima ek olarak de Broglie herhangi bir kapali yorungenin 1 k nin tam kati olmasi varsayimini da kullanarak deneysel olarak gozlenen ve Arnold Sommerfeld ve Bohr tarafindan kuantize olma sartlari olarak anilan sartlari matematiksel olarak kolayca turetti Bu turetme gayet gizemli bir sekilde dogru sonuclar verince Davisson ve Germer 1927 yilinda Bell Laboratuvarlarinda gerceklestirdikleri deneyle elektronlarin da ayni isik gibi girisim yaptigini ortaya koydular Deney 1924 te de Brogli tarafindan onerilmisti insanlar deneysel olarak baska seyleri tahmin etmesini de beklediler Elbette yanildilar cunku bu sartlar serbest isik parcalari icin olusturulan varsayimlarin cekirdege bagli elektronlar icin uyarlanmasiydi ve cok ileri goturulmemesi gerekiyordu Ama dalga mekanigi icin dogru cikis noktasi idi Enteresan bir sekilde 1925 1926 yillari arasinda Werner Heisenberg Max Born Wolfgang Pauli ve Pascual Jordan matris mekanigi ile kuantum mekaniginin formal tanimini yaptilar Ama formalizmlerinde dalga mekanigine yer vermediler Benimsedikleri felsefe ise tamamen pozitivist idi Yani sadece deneysel olarak gozlenebilen degerleri goz onune alan bir yaklasim kullandilar 1926 yilinda Erwin Schrodinger bir dizi denklemle dalga mekanigini yeniden canlandirdi Sonunda kendi dalga mekaniginden Heisenberg in matriks mekanigini de turetip iki formalizmin matematiksel olarak denk oldugunu da gosterdi son makalelerinden birinde Schrodinger relativistik bir dalga denklemi de sunar Dirac a gore ise tarih biraz daha farkli islemistir Ona gore Schrodinger once relativistik dalga denklemini gelistirdi sonra bunu kullanarak hidrojenin spektrumunu hesapladi ve deneylere uymadigini gordu Ancak bu denklemin dusuk hizlarda gecerli olan versiyonu aslinda calisiyordu ve bildigimiz Schrodinger dalga denklemine ulasiliyordu Daha sonra relativistik dalga denklemi Oskar Klein ve Walter Gordon tarafindan yayinladi ve hala Klein Gordon denklemi olarak anilir Bu noktadan sonra Dirac teoriyi ozel gorelilikle uyumlu hale getirmis ve bazi deneylerin sonuclarini teorik olarak uretmistir Ornegin pozitron un varligini 1932 senesinde Carl David Anderson kanitlamistir ve nobel ile odullendirilmistir Kuantum teorisi daha sonra 1940 larda Sin Itiro Tomonaga Julian Schwinger ve Richard P Feynman in kuantum elektrodinamigi konusunda onemli calismalariyla gelisimine devam etmistir 1950 li ve 60 li yillar ise Kuantum renk dinamiginin gelisimine tanik olmustur Gelismeler 1897 Pieter Zeeman isigin bir atom icindeki yuklu parcaciklarin hareketi sonucu yayimlandigini buldu J J Thomson da elektronu kesfetti 1900 Max Planck kara cisim isimasini kuantumlanmis enerji yayimi ile acikladi kuantum kurami boylece dogmus oldu 1905 Albert Einstein dalga ozellikleri olan isigin ayni zamanda daha sonra foton diye adlandirilacak olan belirli buyuklukte enerji paketlerinden olustugu dusuncesini ortaya atti 1911 1913 Ernest Rutherford atomun cekirdek modelini olusturdu Bohr ise atomu bir gezegen sistemi gibi betimledi 1923 Arthur Compton X isinlarinin elektronlarla etkilesimlerinde minyatur bilardo toplari gibi davrandiklarini gozlemledi Boylece isigin parcacik davranisi hakkinda yeni kanitlar ortaya koydu 1923 Louis de Broglie dalga parcacik ikiligini genellestirdi 1924 Satyendra Nath Bose Albert Einstein kuantum parcaciklarini saymak icin diye adlandirilan yeni bir yontem buldular Klasik mekanik kuantum mekanigi ve kuantum mekaniginin matematigiKlasik mekanik nesnelerin konum ve momentumlari bilgilerini kullanarak cesitli kuvvet alanlari altinda nasil hareket etmeleri gerektigini bulmaya calisir Kokleri cok eskiye dayansa da baslangicinin Newton un Principia si oldugunu kabul etmek yanlis olmaz Daha sonra Euler Lagrange Jacobi Hamilton Poisson Maxwell Boltzman Istatiksel mekanik ve klasik elektromanyetik teori de klasik mekanige katilabilir gibi bircok ad tarafindan cok cesitli bakis acilari gelistirilmis ve bircok alanda basarili bir sekilde uygulanmistir Klasik mekanigin tamamlanmasinin Einstein in gorelilik kuramlari ile gerceklestigini soylemek yanlis olur Klasik mekanik cok basarili olmasina karsin 1800 lu yillarin sonlarina dogru siyah cisim isimasi tayf cizgileri fotoelelektrik etki gibi birtakim olaylari aciklamada yetersiz kalmistir Aciklamalarin yanlisligi bilim adamlarinin yetersizliginden degil aksine klasik mekanigin yetersizliginden kaynaklaniyordu Klasik mekanikteki sorunun ne oldugunu anlatmak asiri teknik kacacaktir ancak en yalin halde klasik mekanik evreni surekli olarak modeller ve bu yaklasim kendi icinde tutarli degildir Bunu gormek icin termodinamikteki es dagilim prensibine Ingilizce equipartition theorem bakmaliyiz Uc konum x y z ve uc momentumla px py pz tanimlanan parcaciklar sonsuz sayida parametreyle tanimlanan alanlarla bir aradadir Es dagilim kuraminca sistemin enerjisinin denge durumunda sistemin tum bilesenlerine esit bicimde dagilmasi gerekir Alanlar sonsuz bilesene sahip oldugundan butun enerji alanlara dagilmalidir Daha teknik bir ifade ile denge durumundaki sistemde enerji butun ozgurluk derecelerine es olarak dagilir alanlar sonsuz ozgurluk derecesine sahip oldugu icin butun enerji alanlara akmalidir Evren dengede varsayilirsa deneysel olarak boyle bir gozlemin olmamasi klasik mekanigin sureklilik paradigmasinda bir soruna isaret eder Kuantum kurami ise olayi bambaska bir sekilde ele alir Parcaciklar artik dogrudan 3 konum ve 3 momentumla tanimlanmak yerine bir dalga fonksiyonu ile tanimlanirlar Bu dalga fonksiyonu parcacigin butun bilgisini icinde barindirir ve dalga fonksiyonuna uygun sorular sorularak gerekli bilgi alinir Ornegin konum bilgisi icin dalga fonksiyonuna Parcacik nerede sorusunu sorarsiniz o ise size parcacigin soruyu sordugunuz anda nerede olabilecegini soyler Buradaki kritik nokta olabilirliktir Bu dalga fonksiyonunun bir de olasilik fonksiyonu olarak anilmasina neden olmaktadir Daha sonra bu olasiliksal durumu bilincli olup olmama durumuna baglayan Kopenhag Yorumu ortaya atilmistir Matematik altyapisi yetersiz olanlar denklemleri gormezden gelebilirler Matematiksel olarak olayi soyle tanimlayabiliriz PS x t displaystyle Psi x t parcacigi tanimlayan dalga fonksiyonumuz olsun x PS x t xPS x t dx displaystyle langle x rangle int Psi x t x Psi x t dx integrali bize x in beklenen degerini verir Yukarida bahsedilen soru sorma islemi tam olarak boyle yapilir Benzer sekilde momentumun beklenen degeri icin p PS x t âiddxPS x t dx displaystyle langle p rangle int Psi x t frac hbar i frac d dx Psi x t dx seklinde soruyu sorariz PS x t displaystyle Psi x t dalga fonksiyonumuzun karmasik eslenigidir Karmasik eslenik ve dalga fonksiyonu arasinda kalan ifadeler gozlemlenebilirlerimizin yani konum ve momentumun konum uzayindaki operatorleridir Operatorler sorunun ta kendisidir Konum ve momentum disinda daha bircok gozlemlenebilir ile islem yapilabilir Ancak konum ve momentum operatorleri kullanilarak diger bircok operatoru elde etmek mumkundur Isin ilginc yani bu operatorle elde etmek icin klasik formuller kullanilir Ornegin kinetik enerji klasik mekanikte T p22m displaystyle T frac p 2 2m seklinde tanimlanirken kuantum fiziginde kinetik enerji operatoru yine ayni ifadeyle yazilir Tek fark p artik bir sayi degil bir operatordur Bu bize Ehrenfest teoremince saglanir ve butun operatorleri klasik yasalari kullanarak turetebiliriz Bu noktada Peki dalga fonksiyonu nedir sorusuna donmeliyiz Dalga fonksiyonu bize Schrodinger denklemi tarafindan verilen bir bakima parcacigin kimlik kartidir Bir boyutta Schrodinger denklemi iâddtPS â22md2dx2PS V x t PS displaystyle i hbar frac d dt Psi frac hbar 2 2m frac d 2 dx 2 Psi V x t Psi seklinde yazilabilir Ifade bir bakima enerji denklemidir ve bahsi gecen kimlik kartini sistemin enerjisine gore verir Burada kimlikten kasit parcacigin elektron mu yoksa notron mu oldugu degil momentumu konumu kinetik enerjisi gibi gozlemlenebilir olmalaridir Bu denklem cozuldugunde parcacigimizin dalga fonksiyonunu elde etmis oluruz En basit atom olan hidrojen atomunun zamandan bagimsiz analitik olarak cozulmesi bile zordur neyse ki belli formalizmlerle daha karmasik sistemleri yaklasimlar yaparak cozmek mumkun oluyor Kuantum mekanigi temelinde bir olasilik teorisidir Dalga fonksiyonu icinde sistemin butun olasi durumlarini barindirir Siz soruyu sordugunuzda size en olasi cevabi verir ancak soru sorma islemi dalga fonksiyonunu dagitir ve siz bir daha sordugunuz zaman artik baska bir cevap alirsiniz Bunun yani sira kuantum mekanigi yapisi oturu belirsizlikler barindirir Bu belirsizlikler bazi gozlemlenebilir olani ne kadar iyi bilirseniz diger bazilari hakkinda o kadar az sey bileceginizi soyler Ornegin konum ve momentum boyle bir cift olusturur Birini ne kadar iyi bilirseniz digeri hakkinda o kadar az bilginiz olur Bu Heisenberg belirsizlik ilkesi olarak bilinir Konum ve momentum icin Heisenberg belirsizlik ilkesi soyle gosterilir sxsp â2 displaystyle sigma x sigma p geqslant frac hbar 2 Bu ifade de sx displaystyle sigma x ve sp displaystyle sigma p ile verilenler sirasiyla konum ve momentumdaki belirsizliklerdir Yukarida ele alinan kuantum mekanigi oklidyen bir uzayda calisilmis kuantum mekanigidir diger bir deyisle goreceli degildir Einstein in ozel gorelilik kuramina uyan bir kuantum mekanigi turetmek mumkundur Hatta ilk bakista kolay bir ugrastir Kuantum fikrine ve ozel gorelilige biraz asina olan biri bile cozume kolayca ulasir Yukarida deginilen Schrodinger denklemini daha sade bir formda soyle ele alabiliriz iâ tPS HPS displaystyle i hbar frac partial partial t Psi H Psi Burada H olarak verilen Hamiltonian operatorudur Toplam enerji olarak dusunulebilir Relativistik olmayan serbest parcacik potansiyel enerji sifir icin Hamiltonian H p22m displaystyle H frac p 2 2m olarak verilir Relativistik serbest parcacik icinse Hamiltonian H m2c4 p2c2 displaystyle H sqrt m 2 c 4 p 2 c 2 seklinde yazilabilir Ifade pek yabanci degil degil mi Hayir olaya klasik mekanik acisindan bakarsaniz parcacigin durdugunu kabul edersek momentum sifir olacak ve unlu E mc2 displaystyle E mc 2 yi elde etmis olacaksiniz Simdi relativistik Hamiltonianla Schrodinger denklemini yeniden yazalim iâ 2c2 m2c4ps iâ tps displaystyle sqrt i hbar mathbf nabla 2 c 2 m 2 c 4 psi i hbar frac partial partial t psi Karesi alinirsa 2ps 1c2 2 t2ps m2c2â2ps displaystyle mathbf nabla 2 psi frac 1 c 2 frac partial 2 partial t 2 psi frac m 2 c 2 hbar 2 psi elde edilir Bu denklem Klein Gordon denklemi olarak bilinir Ancak denklem birtakim teknik nedenden oturu sorunludur Daha gecerli relativistik cozum Dirac tarafindan kesfedilmistir ve kendi adiyla anilan denklemle verilir Ultramikroskobik boyutlarda Planck Uzunlugu uzayin kucuk dalga boylarinda bir kaos oldugu dusunulur Evrenin milyarda birinin milyarda birinin milyonda biri boyutlarda gozleyecek olursaniz evren bir kaos olarak gorunur Kuantum mekanigi tarihi gelisimi boyunca bircok sinavdan alninin akiyla cikmayi basarmistir Olgulari buyuk bir dogrulukla aciklamasi yeni olgulara isik tutmasi bir teoriden beklenen ozelliklerdir ve kuantum mekanigi bu isi gercekten oldukca iyi basarmistir Kuantum fikirleri uzerine gelisen kuantum elektrodinamigi QED ve kuantum renk dinamigi QCD bu gune kadarki hicbir teorinin ulasamadigi hassasiyetlerde sonuclar vermislerdir Ne var ki gectigimiz yuzyilin cok buyuk iki teorik acilimi bir biriyle uyusmamaktadir Dogada bilinen 4 kuvvetten 3 u elektromanyetizma zayif ve guclu kuvvetler kuantum kuramlariyla ele alinabilirken kutlecekimin henuz tutarli bir kuantum kurami bulunamamistir Her ne kadar sicim kuramlari kuantum kutlecekime aday gibi gorunse de cozulmesi gereken cok buyuk sorunlar halen bulunmaktadir Gunumuzde yaygin kani kuantum ve kutlecekimin ustunde dogrusal olmayan daha genel bir kuramin yer aldigidir Kuantum mekaniginin uygulamalariKimyasal ve fizik bilimlerinin temelleri su temel arastirma alanlari ustune kuruludur Akiskanlar Mekanigi Elektromanyetik Istatistiksel Mekanik Kimyasal Kinetik Klasik Mekanik Kuantum Mekanigi Optik Termodinamik Diger tum fizik ve kimya dallari bu temel duzeneklerin uygulamalaridir O halde bunlara saf digerlerine uygulamali fizik ve kimya gozu ile bakilabilir Kuantum mekaniginin mikro sistemlere uygulanmasi ile su uygulamali fizik ve kimya dallari turetilmistir Anorganik Kimya Organik Kimya Biyokimya Bunlar da temel uygulama dali olan Kuantum Kimyasi nin ozel olarak sirasiyla anorganik organik ve biyomolekullere olan uygulamasidir Kati Hal Kimyasi Fizigi Kati halin kuantum mekanigi Kuantum Kimyasi Atom ve molekullerin kuantum mekanigi Fizik te genelde Atom ve Molekul Fizigi ismi tercih edilir Nukleer Kimya Fizik Cekirdegin kuantum mekanigi Parcacik Kimyasi Fizigi Atomalti parcaciklarin kuantum mekanigi Plazma Kimyasi Fizigi Plazmanin kuantum mekanigi Sivi Hal Kimyasi Fizigi Sivi halin kuantum mekanigi Fotokimya ve fotofizik yuzey kimyasi vb pek cok dal da kuantum mekaniginden uygulamalar icermektedir Kuantum mekanigi her ne kadar cok kucuklerin dunyasini modelleyen bir kuram olsa da uygulama alanlari gerek dolaysiz gerek dolayli yollarla cok genistir Kuantum mekanigi biyoloji malzeme bilimi elektronik gibi bircok alanin gunumuzdeki anlamina kavusmasini saglamistir Laser maser yari iletkenler gibi gunumuzun olmazsa olmazlarinin icatlari kuantum mekanigi sayesinde mumkun olmustur Ayrica elektron mikroskobu atomik kuvvet mikroskobu taramali tunellemeli mikroskop gibi biyoloji ve nanoteknolojik uygulamalarin olmazsa olmazlari PET Scan Positron Emmission Tomography MRI Magnetic Resonance Imaging Tomografi gibi tibbi goruntuleme cihazlari yine kuantum mekaniginin bize gosterdigi belli doga olgularini kullanarak calisirlar Yine tip nanoteknoloji elektronik gibi bircok alanda sayisiz kullanimi olan fiberler kuantum mekaniginin dogrudan uygulamasina ornektir Modern kimya kuantum fikirleri uzerine insa edilmis ve cok karmasik molekullerin yapilari bu sayede anlasilmistir Kuantum mekanigi felsefesiKuantum mekanigi bugune kadar girdigi tum sinavlardan basariyla cikmistir Peki nasil olur da bu denli basarili bir teorinin elestirel bir felsefesinden soz edilebilir Dahasi teorinin bazi felsefi sorular ortaya cikardigini nasil ileri surebiliriz Kuantum mekanigi net ve saglam matematik temeller uzerine kurulmustur Sistemlerin dogasi bu matematikle modellenir Ancak basli basina bu modelleme kuantum mekaniginin temel kavramlarinin cozumlenmesinde felsefecilere gore yetersizdir Ornek verecek olursak PS x t displaystyle Psi x t bir dalga fonksiyonudur Bu dalga fonksiyonunun mutlak karesinin olasilik genligi oldugu ise bir yorumdur Istatistiki bir dagilimi temsil eden olasilik genliginin altta yatan fiziksel gerceklik ile baglantisini sorgularsak ve bunu genel bir cerceveye oturtmak istersek o zaman kuantum mekanigi felsefesi yapmis oluruz Fizikciler arasinda genel yaklasim felsefe yapmak yerine degisik kosullar altinda Schrodinger denklemini cozmek ve teorik olarak bulunan sonuclari deneysel sonuclar ile karsilastirmaktir Simdiye kadar deneyler bu sekilde hep basari ile aciklanabilmistir yani doga kuantum mekaniginin tahminlerine gore hareket etmektedir Burada uzerinde durulabilecek bir nokta kuantum fiziginin uzerinde deney yapilmasi imkansiz kavramlarin felsefesini yapmaya gerek duymamasi bunun yerine sadece deney ve teorinin uyumuna bakmasidir Kuantum mekanigi tamamlanmis bir teori midir Kuantum mekaniginin temelleri Heisenberg belirsizlik ilkesinin formule edildigi 1927 yilindan bu zamana dek hicbir degisiklige ugramamistir Kuantum mekaniginin uzantisi olarak ortaya cikan teorilerde ortaya cikan kavramlar da bildigimiz kadariyla bu temel ilkelerde degisiklik yapilmasini gerektirmezler Kuantum mekanigi dogdugu andan itibaren temel ilkelerin anlasilmasi bakimindan buyuk tartismalara yol acmistir Bu tartismalardan biri A Einstein B Podolsky ve N Rosen in 1935 yilinda Doganin Kuantum Mekaniksel Tasviri Tamamlanmis Kabul Edilebilir mi basligiyla yayinladiklari ve yazarlarinin adlarinin bas harfleriyle EPR Paradoksu olarak adlandirilan makalesiyle baslamis olup halen de onemini korumaktadir EPR makalesi bir fizik teorisinin tamamlanmis kabul edilebilmesi icin iki temel kosulu yerine getirmesi gerektigini soyler Bunlar Teorinin dogrulugu Teorinin tamamlanmisligi EPR makalesine gore teorinin dogru olarak nitelendirilebilmesi icin teorinin deney sonuclariyla uyumlulugu goz onune alinmalidir Bu bakimdan kuantum mekanigi deneylerle buyuk bir uyum gosterdigi icin dogru kabul edilir Teorinin basarisi icin gerekli olan diger kosul olan tamamlanmislik icin ise makalede su kosul verilmistir Bir fizik kuraminda her fiziksel gerceklige karsilik olan bir oge bulunmalidir Makalede fiziksel gerceklik su sekilde tanimlanmistir Bir fiziksel niceligin degerini dinamik sistemi herhangi bir bicimde bozmaksizin kesinlikle tahmin edebiliyorsak o zaman fiziksel gercekligin bu fiziksel nicelige karsilik olan bir ogesi vardir Fiziksel niceligin kesin bir degerini dinamik sistemi bozmadan teoride elde edebiliyorsak o zaman teoriden hesap ile elde edilen bu kesin deger fiziksel gercekligin bir ogesine karsilik gelecektir Ancak fiziksel gercekligin butun ogelerinin fizik teorisinde karsiliklarinin bulunmasi gerektigine dair bir kosul ileri surulmemistir Bu nedenle EPR ye gore dogru olan teorinin ayni zamanda tamamlanmis olmasi gerekmez Fiziksel gerceklik olcutunun kuantum mekanigi cercevesinde nasil kullanildigi makalede su ornekle aciklanmistir Elimizdeki parcacik F p displaystyle Phi p fonksiyonu ile gosterilsin Fonksiyonu F p jajÏj p displaystyle Phi p sum j a j phi j p seklinde gosterelim Bu parcacigin momentumu olculmeden once su onerme ileri surulebilir Parcacigin momentumunun olcumden sonra pi displaystyle p i degerini alma olasiligi ai 2 displaystyle a i 2 dir Ayrica j aj 2 1 displaystyle sum j a j 2 1 oldugunu kabul edelim Eger alinabilecek birden cok momentum degeri mevcutsa ai 2 displaystyle a i 2 1 e esit degildir Bu sebepten oturu fiziksel gerceklik olcutu bu durumda kullanilamaz KitapDers kitaplari J J Sakurai J Napolitano Modern Kuantum Mekanigi Palme Yayincilik 2012 ISBN 9780805382914 T Dereli Kuantum Mekanigi I ODTU Yayincilik ISBN 9789757064091 E Aygun M Zengin Kuantum Fizigi Ankara Universitesi Yayinlari 2 baski 1992 J J Sakurai Advanced Quantum Mechanics Addison Wesley 1967 ISBN 9780201067101 E Rizaoglu M Yalcinkaya O Gultekin Alfa Yayinlari 2021 ISBN 9786254492068 Fizigin diger alanlari hakkinda yazilan ilgili ders kitaplari B H Bransden C J Joachain Atom ve Molekul Fizigi On Dokuz Mayis Universitesi Yayinlari T N Durlu Kati Hal Fizigine Giris Ankara Universitesi Yayinlari 2 baski 1992 E Aygun M Zengin Atom ve Molekul Fizigi Ankara Universitesi Yayinlari 1992 D Halliday R Resnick Fizigin Temelleri 2 Palme Yayincilik A Beiser Cagdas Fizigin Kavramlari Dicle Universitesi Yayinlari 2 baski 1989 C Onem Fizikte Matematik Metotlar Birsen Yayincilik 3 baski KaynakcaOzel Caykara Emine 1964 Oktay Sinanoglu Kitabi Turk Aynstayni Turkiye Is Bankasi Kultur Yayinlari s 178 ISBN 9754582947 Nihat Taspinar Dalga mekanigi stokes 3 mertebe dalga teorisi ve tablolari Dokuz Eylul Universitesi 1987 291 sayfa a b Quantum mechanics 11 Temmuz 2014 tarihinde Wayback Machine sitesinde Britannica com 10 Agustos 2014 quantum 12 Agustos 2014 tarihinde Wayback Machine sitesinde Online Etymology Dictionary 10 Agustos 2014 mechanics Oxford Dictionary of English 2e Oxford University Press 2003 Otomatik Cizgi Tanimi Programi PDF T C Istanbul Universitesi Fen Bilimleri Enstitusu 27 Mart 2021 tarihinde kaynagindan PDF Erisim tarihi 20 Subat 2021 a b PDF 11 Ocak 2020 tarihinde kaynagindan PDF arsivlendi Britannica 19 Haziran 2015 tarihinde kaynagindan arsivlendi J J Thompson And The Discovery Of The Electron E A Davis Isabel Falconer PDF Dr A Kursad Poyraz F U Tip Fakultesi Radyoloji A D 28 Eylul 2020 tarihinde kaynagindan PDF arsivlendi Elektro Manyetik Teori PDF O Cakir AU XII Ulusal Parcacik Hizlandiricilari ve Dedektorleri Yaz Okulu HTE Golbasi 2 7 Temmuz 2018 27 Mart 2021 tarihinde kaynagindan PDF Erisim tarihi 20 Subat 2021 Elektro Manyetik Alan Teorisi PDF Yardimci Doktor Docent Aslan Unal in not defteri Yardimci Doktor Docent Aslan Unal 27 Mart 2021 tarihinde kaynagindan PDF Erisim tarihi 20 Subat 2021 a b c Niels Bohr un biyografisi Britannica 7 Temmuz 2015 tarihinde kaynagindan arsivlendi KUANTUM AYAR ALAN TEORILERININ KUANTIZASYONU VE STANDART MODEL PDF PROF DR MUGE BOZ EVINAY Hacettepe Universitesi 2015 27 Mart 2021 tarihinde kaynagindan PDF Erisim tarihi 20 Subat 2021 a b Bohr un Atom modellerinin yetersizlikleri Psiko fizik 7 Mayis 2021 tarihinde kaynagindan Erisim tarihi 20 Subat 2021 Britannica 7 Temmuz 2015 tarihinde kaynagindan arsivlendi a b c Louis de Broglie nin Biyografisi calismasi Britannica 7 Temmuz 2015 tarihinde kaynagindan arsivlendi Elizabeth H Oakes Encyclopedia of World Scientists Facts on File Science Library 2007 s 19 ISBN 13 9780816061587 GenelKuantum Fizigi 1 2 27 Eylul 2007 tarihinde Wayback Machine sitesinde Kuantum Fizigi 2 2 27 Eylul 2007 tarihinde Wayback Machine sitesinde Ayrica bakinizCogul dunyalar yorumu Kopenhag yorumu Pilot dalga kurami Von Neumann yorumuDis baglantilarCERN26 Temmuz 2007 tarihinde Wayback Machine sitesinde Kuantum Teorisi ve Atomalti Parcaciklar 9 Mayis 2018 tarihinde Wayback Machine sitesinde
 AzÉrbaycanca
AzÉrbaycanca ĐДлаŃŃŃĐșŃ
ĐДлаŃŃŃĐșŃ Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana æ„æŹèȘ
æ„æŹèȘ ÒĐ°Đ·Đ°Ò
ÒĐ°Đ·Đ°Ò Lietuvos
Lietuvos Nederlands
Nederlands PortuguĂȘs
PortuguĂȘs Đ ŃŃŃĐșĐžĐč
Đ ŃŃŃĐșĐžĐč à·à·à¶à·à¶œ
à·à·à¶à·à¶œ àčàžàžàčàžàžą
àčàžàžàčàžàžą TĂŒrkçe
TĂŒrkçe ĐŁĐșŃĐ°ŃĐœŃŃĐșĐ°
ĐŁĐșŃĐ°ŃĐœŃŃĐșĐ° äžćäșș
äžćäșș United State
United State Afrikaans
Afrikaans