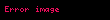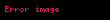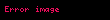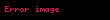Matematiksel analizde Legendre fonksiyonları, aşağıdaki Legendre diferansiyel denkleminin çözümleridir.
- ;
Bu adi diferansiyel denklem daha çok fizikte ve diğer teknik alanlarda kullanılır. Özellikle küresel koordinat sisteminde, kısmi diferansiyel denklem ile ilgili Laplace denklemi çözerken ortaya çıkar.
Özyineli tanımlama
Aşağıdaki genişletilmiş Taylor serisidir;
(Denklem I)
(Denklem I)'in ilk iki terimini ele alalım:
Bu ilk iki terim Legendre polinomudur. Diğer birkaç Legendre polinomları şunlardır:
| n |  |
| 0 |  |
| 1 |  |
| 2 |  |
| 3 |  |
| 4 |  |
| 5 |  |
| 6 |  |
| 7 |  |
| 8 |  |
| 9 |  |
| 10 |  |

Çözümü
Legendre fonksiyonu, [-1,1] aralığında tanımlı, ±1 noktalarında kaldırılabilir tekilliğe sahip bir denklemdir. Kapalı formu şu şekilde gösterilir.
Burada L, Legendre operatörüdür.
Denklem Frobenius yöntemi ile, p=0 alınarak çözülürse.
ifadeleri denklemde yerlerine koyularak,
Bu eşitlikten çıkan karakteristik denklem ise:
olur. Genellenirse
Bu şekilde geriye dönerek tekrarlanarak çözüm bulunur. Çözümün sonlu olabilmesi için
şartı sağlanması gerektiğinden, karakteristik denklem yardımıyla elde edilen çözümün sonlu olması ancak
şeklinde serinin kesilmesi ile olur. Bu şekilde oluşan polinomlara Legendre polinomları denir ve dolayısıyla bu polinomlar Legendre diferansiyel denkleminin çözümüdür.
Legendre polinomlarının ek özellikleri
Legendre polinomları simetrik veya antisimetriktir, Şöyle ki
diferansiyel denklem ve diklik özellikleri yardımıyla ölçeklemenin bağımsızlığı,"standardlaştırılmış" (bazen "normalizasyon" denir, ama unutmamalıki güncel norm birim değildir) böylece ölçekleme ile Legendre polinomları'nın tanımı
ve son noktada türev ile veriliyor
yukardaki soruda,Bonnet’in yineleme formülünde üç özyineleme ilişkisi terimi,bilinen Legendre polinomları ile uyumludur
ve
Legendre polinomlarının integrasyonu için kullanışlıdır;
yukardakinden şu görülebilir
veya eşdeğeri
burada 
Bonnet’in yineleme formülünden açık gösterim bir endüksiyon ile
elde edilir.'nden Legendre polinomları için okunan
Legendre polinomlarının bir toplamı 

bir Legendre polinomları küresel harmonikler ile kullanılan açılımı kullanılabilir
burada sırasıyla birim vektörler r ve r' küresel koordinatlar 

Asimptotiklik 
ve birimden büyük eklentiler için
burada 

Legendre polinomlarının kayması
Kayan Legendre polinomları 


kayan Legendre polinomu için bir
açık bağıntı ile veriliyor
kayan Legendre polinomları için analoğu
ilk birkaç kayan Legendre polinomlarıdır:
| n |  |
| 0 | 1 |
| 1 |  |
| 2 |  |
| 3 |  |
| 4 |  |
Legendre fonksiyonları
Polinom çözümleri yanında, Legendre denkleminin polinomal-olmayan çözümlerinin sonsuz seriler ile gösterimi var. Bu ikinci türün Legendre fonksiyonlarıdır,
Diferansiyel denklem
genel çözümü var
,
burada A ve B sabitlerdir.
Kesirli derecenin Legendre fonksiyonları
Kesirli dereceli Legendre fonksiyonları ve ile tanımlanan kesirli türevlerin başlangıç noktasından ve tam sayı-olmayan faktöriyeller ( ile tanımlanır) içinde aşağıdadır. Sonuç fonksiyonlar Legendre diferansiyel denklem aracılığıyla (−1,1) yeterli sürekliliktedir,ama son noktasında bundan böyle düzenlidir. P0n ile Kesirli dereceli Legendre fonksiyonu Pn uyumludur.
Ayrıca bakınız
Notlar
- ^ George B. Arfken, Hans J. Weber, Mathematical Methods for Physicists, Elsevier Academic Press, 2005, pg. 753.
Kaynakça
- Bayin, S.S. (2006), Mathematical Methods in Science and Engineering, Wiley, Chapter 2.
- Belousov, S. L. (1962), Tables of normalized associated Legendre polynomials, Mathematical tables, 18, Pergamon Press.
- ; Hilbert, David (1953), Methods of Mathematical Physics, Volume 1, New York: Interscience Publischer, Inc.
- Refaat El Attar (2009), Legendre Polynomials and Functions, CreateSpace, ISBN
Dış bağlantılar
- A quick informal derivation of the Legendre polynomial in the context of the quantum mechanics of hydrogen19 Haziran 2010 tarihinde Wayback Machine sitesinde .
- Hazewinkel, Michiel, (Ed.) (2001), "Legendre polynomials", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN
- Wolfram MathWorld entry on Legendre polynomials6 Mart 2010 tarihinde Wayback Machine sitesinde .
- Dr James B. Calvert's article on Legendre polynomials from his personal collection of mathematics27 Nisan 2006 tarihinde Wayback Machine sitesinde .
- Legendre Polynomials from Hyperphysics 6 Ekim 2014 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematiksel analizde Legendre fonksiyonlari asagidaki Legendre diferansiyel denkleminin cozumleridir L ddx 1 x2 ddx l l 1 y displaystyle L d over dx 1 x 2 d over dx l l 1 y l 0 Z displaystyle l in 0 mathbb Z Bu adi diferansiyel denklem daha cok fizikte ve diger teknik alanlarda kullanilir Ozellikle kuresel koordinat sisteminde kismi diferansiyel denklem ile ilgili Laplace denklemi cozerken ortaya cikar Ozyineli tanimlamaAsagidaki genisletilmis Taylor serisidir 11 2xt t2 n 0 Pn x tn displaystyle frac 1 sqrt 1 2xt t 2 sum n 0 infty P n x t n qquad Denklem I Denklem I in ilk iki terimini ele alalim P0 x 1 P1 x x displaystyle P 0 x 1 quad P 1 x x Bu ilk iki terim Legendre polinomudur Diger birkac Legendre polinomlari sunlardir n Pn x displaystyle P n x 0 1 displaystyle 1 1 x displaystyle x 2 12 3x2 1 displaystyle begin matrix frac 1 2 end matrix 3x 2 1 3 12 5x3 3x displaystyle begin matrix frac 1 2 end matrix 5x 3 3x 4 18 35x4 30x2 3 displaystyle begin matrix frac 1 8 end matrix 35x 4 30x 2 3 5 18 63x5 70x3 15x displaystyle begin matrix frac 1 8 end matrix 63x 5 70x 3 15x 6 116 231x6 315x4 105x2 5 displaystyle begin matrix frac 1 16 end matrix 231x 6 315x 4 105x 2 5 7 116 429x7 693x5 315x3 35x displaystyle begin matrix frac 1 16 end matrix 429x 7 693x 5 315x 3 35x 8 1128 6435x8 12012x6 6930x4 1260x2 35 displaystyle begin matrix frac 1 128 end matrix 6435x 8 12012x 6 6930x 4 1260x 2 35 9 1128 12155x9 25740x7 18018x5 4620x3 315x displaystyle begin matrix frac 1 128 end matrix 12155x 9 25740x 7 18018x 5 4620x 3 315x 10 1256 46189x10 109395x8 90090x6 30030x4 3465x2 63 displaystyle begin matrix frac 1 256 end matrix 46189x 10 109395x 8 90090x 6 30030x 4 3465x 2 63 CozumuLegendre fonksiyonu 1 1 araliginda tanimli 1 noktalarinda kaldirilabilir tekillige sahip bir denklemdir Kapali formu su sekilde gosterilir Ly 0 displaystyle Ly 0 Burada L Legendre operatorudur Denklem Frobenius yontemi ile p 0 alinarak cozulurse y n 0 anxn displaystyle y sum n 0 infty a n x n y n 0 nanxn 1 displaystyle y sum n 0 infty na n x n 1 y n 0 n n 1 anxn 2 displaystyle y sum n 0 infty n n 1 a n x n 2 ifadeleri denklemde yerlerine koyularak Ly displaystyle Ly 1 x2 y 2xy l l 1 y displaystyle big 1 x 2 y 2xy l l 1 y 1 x2 n 0 n n 1 anxn 2 2x n 0 nanxn 1 l l 1 n 0 anxn displaystyle 1 x 2 sum n 0 infty n n 1 a n x n 2 2x sum n 0 infty na n x n 1 l l 1 sum n 0 infty a n x n n 0 n n 1 2n l l 1 anxn n 0 n n 1 anxn 2 displaystyle sum n 0 infty left n n 1 2n l l 1 right a n x n sum n 0 infty n n 1 a n x n 2 n 0 l2 n2 l n anxn n 2 n 2 n 1 an 2xn displaystyle sum n 0 infty left l 2 n 2 l n right a n x n sum n 2 infty n 2 n 1 a n 2 x n n 0 l n 1 l n an n 2 n 1 an 2 xn displaystyle sum n 0 infty left l n 1 l n a n n 2 n 1 a n 2 right x n 0 displaystyle 0 Bu esitlikten cikan karakteristik denklem ise a2 l l 1 2a0 displaystyle a 2 l l 1 over 2 a 0 olur Genellenirse an 2 l n 1 l n n 2 n 1 an displaystyle a n 2 l n 1 l n over n 2 n 1 a n Bu sekilde geriye donerek tekrarlanarak cozum bulunur Cozumun sonlu olabilmesi icin limn an 2xn 2anxn lt 1 displaystyle lim n to infty left a n 2 x n 2 over a n x n right lt 1 sarti saglanmasi gerektiginden karakteristik denklem yardimiyla elde edilen cozumun sonlu olmasi ancak n l veya n l 1 displaystyle n l mbox veya n l 1 seklinde serinin kesilmesi ile olur Bu sekilde olusan polinomlara Legendre polinomlari denir ve dolayisiyla bu polinomlar Legendre diferansiyel denkleminin cozumudur Legendre polinomlarinin ek ozellikleriLegendre polinomlari simetrik veya antisimetriktir Soyle ki Pn x 1 nPn x displaystyle P n x 1 n P n x diferansiyel denklem ve diklik ozellikleri yardimiyla olceklemenin bagimsizligi standardlastirilmis bazen normalizasyon denir ama unutmamaliki guncel norm birim degildir boylece olcekleme ile Legendre polinomlari nin tanimi Pn 1 1 displaystyle P n 1 1 ve son noktada turev ile veriliyor Pn 1 n n 1 2 displaystyle P n 1 frac n n 1 2 yukardaki soruda Bonnet in yineleme formulunde uc ozyineleme iliskisi terimi bilinen Legendre polinomlari ile uyumludur n 1 Pn 1 x 2n 1 xPn x nPn 1 x displaystyle n 1 P n 1 x 2n 1 xP n x nP n 1 x ve x2 1nddxPn x xPn x Pn 1 x displaystyle x 2 1 over n d over dx P n x xP n x P n 1 x Legendre polinomlarinin integrasyonu icin kullanislidir 2n 1 Pn x ddx Pn 1 x Pn 1 x displaystyle 2n 1 P n x d over dx left P n 1 x P n 1 x right yukardakinden su gorulebilir ddxPn 1 x 2n 1 Pn x 2 n 2 1 Pn 2 x 2 n 4 1 Pn 4 x displaystyle d over dx P n 1 x 2n 1 P n x 2 n 2 1 P n 2 x 2 n 4 1 P n 4 x ldots veya esdegeri ddxPn 1 x 2Pn x Pn x 2 2Pn 2 x Pn 2 x 2 displaystyle d over dx P n 1 x 2P n x over P n x 2 2P n 2 x over P n 2 x 2 ldots burada Pn x displaystyle P n x 1 x 1 araligindaki normdur Pn x 11 Pn x 2dx 22n 1 displaystyle P n x sqrt int 1 1 P n x 2 dx sqrt frac 2 2n 1 Bonnet in yineleme formulunden acik gosterim bir enduksiyon ile Pn x k 0n 1 k nk 2 1 x2 n k 1 x2 k displaystyle P n x sum k 0 n 1 k begin pmatrix n k end pmatrix 2 left frac 1 x 2 right n k left frac 1 x 2 right k elde edilir nden Legendre polinomlari icin okunan j 0nPj x 0 x 1 displaystyle sum j 0 n P j x geq 0 qquad x geq 1 Legendre polinomlarinin bir toplami 1 y 1 displaystyle 1 leq y leq 1 icin ve 1 x 1 displaystyle 1 leq x leq 1 icin Dirac delta fonksiyonuya iliskilidir d y x 12 ℓ 0 2ℓ 1 Pℓ y Pℓ x displaystyle delta y x frac 1 2 sum ell 0 infty 2 ell 1 P ell y P ell x bir Legendre polinomlari kuresel harmonikler ile kullanilan acilimi kullanilabilir Pℓ r r 4p2ℓ 1 m ℓℓYℓm 8 ϕ Yℓm 8 ϕ displaystyle P ell r cdot r frac 4 pi 2 ell 1 sum m ell ell Y ell m theta phi Y ell m theta phi burada sirasiyla birim vektorler r ve r kuresel koordinatlar 8 ϕ displaystyle theta phi ve 8 ϕ displaystyle theta phi var Asimptotiklik ℓ displaystyle ell rightarrow infty birimden yoksun eklentiler icin Pℓ cos 8 J0 ℓ8 O ℓ 1 22pℓsin 8cos ℓ 12 8 p4 O ℓ 1 displaystyle P ell cos theta J 0 ell theta mathcal O ell 1 frac 2 sqrt 2 pi ell sin theta cos left left ell frac 1 2 right theta frac pi 4 right mathcal O ell 1 ve birimden buyuk eklentiler icin Pℓ 11 e2 I0 ℓe O ℓ 1 12pℓe 1 e ℓ 1 2 1 e ℓ 2 O ℓ 1 displaystyle P ell left frac 1 sqrt 1 e 2 right I 0 ell e mathcal O ell 1 frac 1 sqrt 2 pi ell e frac 1 e ell 1 2 1 e ell 2 mathcal O ell 1 burada J0 displaystyle J 0 ve I0 displaystyle I 0 Bessel fonksiyonlaridir Legendre polinomlarinin kaymasiKayan Legendre polinomlari Pn x Pn 2x 1 displaystyle tilde P n x P n 2x 1 olarak tanimlanir Burada kayan fonksiyon x 2x 1 displaystyle x mapsto 2x 1 aslinda bu bir dur boylece secilen bu 0 1 araligindan 1 1 araligina vurgusu yapilan Pn x displaystyle tilde P n x polinomlari 0 1 arasinda bulunur 01Pm x Pn x dx 12n 1dmn displaystyle int 0 1 tilde P m x tilde P n x dx 1 over 2n 1 delta mn kayan Legendre polinomu icin bir Pn x 1 n k 0n nk n kk x k displaystyle tilde P n x 1 n sum k 0 n n choose k n k choose k x k acik baginti ile veriliyor kayan Legendre polinomlari icin analogu Pn x 1n dndxn x2 x n displaystyle tilde P n x frac 1 n d n over dx n left x 2 x n right ilk birkac kayan Legendre polinomlaridir n Pn x displaystyle tilde P n x 0 11 2x 1 displaystyle 2x 1 2 6x2 6x 1 displaystyle 6x 2 6x 1 3 20x3 30x2 12x 1 displaystyle 20x 3 30x 2 12x 1 4 70x4 140x3 90x2 20x 1 displaystyle 70x 4 140x 3 90x 2 20x 1 Legendre fonksiyonlariPolinom cozumleri yaninda Legendre denkleminin polinomal olmayan cozumlerinin sonsuz seriler ile gosterimi var Bu ikinci turun Legendre fonksiyonlaridir Qn x displaystyle Q n x ile ifade edilir Qn x n 1 3 2n 1 x n 1 n 1 n 2 2 n 3 x n 3 n 1 n 2 n 3 n 4 2 4 2n 3 2n 5 x n 5 displaystyle Q n x frac n 1 3 cdots 2n 1 left x n 1 frac n 1 n 2 2 n 3 x n 3 frac n 1 n 2 n 3 n 4 2 4 2n 3 2n 5 x n 5 cdots right Diferansiyel denklem ddx 1 x2 ddxf x n n 1 f x 0 displaystyle d over dx left 1 x 2 d over dx f x right n n 1 f x 0 genel cozumu var f x APn x BQn x displaystyle f x AP n x BQ n x burada A ve B sabitlerdir Kesirli derecenin Legendre fonksiyonlariKesirli dereceli Legendre fonksiyonlari ve ile tanimlanan kesirli turevlerin baslangic noktasindan ve tam sayi olmayan faktoriyeller ile tanimlanir icinde asagidadir Sonuc fonksiyonlar Legendre diferansiyel denklem araciligiyla 1 1 yeterli surekliliktedir ama son noktasinda bundan boyle duzenlidir P0 n ile Kesirli dereceli Legendre fonksiyonu Pn uyumludur Ayrica bakinizMatematiksel fonksiyonlarin listesi Turan esitsizligiNotlar George B Arfken Hans J Weber Mathematical Methods for Physicists Elsevier Academic Press 2005 pg 753 KaynakcaBayin S S 2006 Mathematical Methods in Science and Engineering Wiley Chapter 2 Belousov S L 1962 Tables of normalized associated Legendre polynomials Mathematical tables 18 Pergamon Press Hilbert David 1953 Methods of Mathematical Physics Volume 1 New York Interscience Publischer Inc Refaat El Attar 2009 Legendre Polynomials and Functions CreateSpace ISBN 978 1 4414 9012 4 Dis baglantilarA quick informal derivation of the Legendre polynomial in the context of the quantum mechanics of hydrogen19 Haziran 2010 tarihinde Wayback Machine sitesinde Hazewinkel Michiel Ed 2001 Legendre polynomials Encyclopaedia of Mathematics Kluwer Academic Publishers ISBN 978 1556080104 Wolfram MathWorld entry on Legendre polynomials6 Mart 2010 tarihinde Wayback Machine sitesinde Dr James B Calvert s article on Legendre polynomials from his personal collection of mathematics27 Nisan 2006 tarihinde Wayback Machine sitesinde Legendre Polynomials from Hyperphysics 6 Ekim 2014 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State