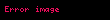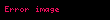Olasılık kuramı ve istatistik bilim kollarında, logistik dağılım bir sürekli olasılık dağılımdır. Logistik dağılımın bir ve bu fonksiyon ve konularında da rol oynar.
Olasılık yoğunluk fonksiyonu | |
Yığmalı dağılım fonksiyonu | |
| Parametreler | (reel) (reel) |
|---|---|
| Olasılık yoğunluk fonksiyonu (OYF) | |
| Birikimli dağılım fonksiyonu (YDF) | |
| Ortalama | |
| Medyan | |
| Mod | |
| Varyans | |
| Çarpıklık | |
| Fazladan basıklık | |
| Entropi | |
| Moment üreten fonksiyon (mf) | for , beta fonksiyonu |
| Karakteristik fonksiyon | for |
Şekil bakımından çan şeklinde olan normal dağılıma çok benzer; fakat kuyrukları daha ağır olduğu için daha basık bir şekil gösterir.
Tanımlama
Yığmalı dağılım fonksiyonu
Logistik dağılım ismini yığmalı dağılım fonksiyonuna atıfla alır çünkü bu fonksiyon matematiksel logistik fonksiyonlar ailesinin bir üyesidir:
Olasılık yoğunluk fonksiyonu
Logistik dağılım için olasılık yoğunluk fonksiyonu (OYF) şu formülle ifade edilir:
OYF bir hiperbolik sekant fonksiyonunun karesi şeklinde olduğu görülür.
Kuantil fonksiyonu
Logistik fonksiyon için ters yığmalı dağılım fonksiyonu fonksiyonunun bir genelleştirilmesi suretiyle 
Alternatif şekilde parametreleme
Logistik dağılım için bir alternatif parametreleme 
Uygulamalar
Milletlerarası satranç federasyonu FIDE ve bunun üyesi olan birçok milli satranç federasyonu satranç oyuncularının sınıflandırılması için kullanılan formüllerde logistik dağılım kullanmaya başlamışlardır.
İlişkili dağılımlar
Eğer X bir logistik fonksiyona göre dağılım gösteriyorsa log(X) bir şeklindedir ve log(X - a) bir gösterir.
Kaynakça
Balakrishnan, N. (1992). Handbook of the Logistic Distribution. Marcel Dekker, New York. .
Johnson,, N.L. (1995). Continuous Univariate Distributions Vol.2. Marcel Dekker, New York. .
İçsel kaynaklar
- İngilizce Vikipedia Logistic distribution maddesi
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Olasilik kurami ve istatistik bilim kollarinda logistik dagilim bir surekli olasilik dagilimdir Logistik dagilimin bir ve bu fonksiyon ve konularinda da rol oynar Logistik Olasilik yogunluk fonksiyonuYigmali dagilim fonksiyonuParametreler m displaystyle mu reel s gt 0 displaystyle s gt 0 reel x displaystyle x in infty infty Olasilik yogunluk fonksiyonu OYF e x m ss 1 e x m s 2 displaystyle frac e x mu s s left 1 e x mu s right 2 Birikimli dagilim fonksiyonu YDF 11 e x m s displaystyle frac 1 1 e x mu s Ortalama m displaystyle mu Medyan m displaystyle mu Mod m displaystyle mu Varyans p23s2 displaystyle frac pi 2 3 s 2 Carpiklik 0 displaystyle 0 Fazladan basiklik 6 5 displaystyle 6 5 Entropi ln s 2 displaystyle ln s 2 Moment ureten fonksiyon mf emtB 1 st 1 st displaystyle e mu t mathrm B 1 s t 1 s t for st lt 1 displaystyle s t lt 1 beta fonksiyonuKarakteristik fonksiyon eimtB 1 ist 1 ist displaystyle e i mu t mathrm B 1 ist 1 ist for ist lt 1 displaystyle ist lt 1 Sekil bakimindan can seklinde olan normal dagilima cok benzer fakat kuyruklari daha agir oldugu icin daha basik bir sekil gosterir TanimlamaYigmali dagilim fonksiyonu Logistik dagilim ismini yigmali dagilim fonksiyonuna atifla alir cunku bu fonksiyon matematiksel logistik fonksiyonlar ailesinin bir uyesidir F x m s 11 e x m s displaystyle F x mu s frac 1 1 e x mu s 12 12tanh x m2s displaystyle frac 1 2 frac 1 2 operatorname tanh left frac x mu 2 s right dd Olasilik yogunluk fonksiyonu Logistik dagilim icin olasilik yogunluk fonksiyonu OYF su formulle ifade edilir f x m s e x m ss 1 e x m s 2 displaystyle f x mu s frac e x mu s s left 1 e x mu s right 2 14ssech2 x m2s displaystyle frac 1 4 s operatorname sech 2 left frac x mu 2 s right dd OYF bir hiperbolik sekant fonksiyonunun karesi seklinde oldugu gorulur Kuantil fonksiyonu Logistik fonksiyon icin ters yigmali dagilim fonksiyonu fonksiyonunun bir genellestirilmesi suretiyle F 1 displaystyle F 1 olarak elde edilir ve bu da soyle tanimlanir F 1 p m s m sln p1 p displaystyle F 1 p mu s mu s ln left frac p 1 p right Alternatif sekilde parametrelemeLogistik dagilim icin bir alternatif parametreleme s2 p2s2 3 displaystyle sigma 2 pi 2 s 2 3 esitligi kullanarak terimlerin degistirilmesi suretiyle elde edilebilir Boylece logistik dagilim icin yogunluk fonskiyonu soyle degisik sekilde ifade edilebilir g x m s f x m s3 p ps43sech2 p23x ms displaystyle g x mu sigma f x mu sigma sqrt 3 pi frac pi sigma 4 sqrt 3 operatorname sech 2 left frac pi 2 sqrt 3 frac x mu sigma right UygulamalarMilletlerarasi satranc federasyonu FIDE ve bunun uyesi olan bircok milli satranc federasyonu satranc oyuncularinin siniflandirilmasi icin kullanilan formullerde logistik dagilim kullanmaya baslamislardir Iliskili dagilimlarEger X bir logistik fonksiyona gore dagilim gosteriyorsa log X bir seklindedir ve log X a bir gosterir KaynakcaBalakrishnan N 1992 Handbook of the Logistic Distribution Marcel Dekker New York ISBN 0 8247 8587 8 Johnson N L 1995 Continuous Univariate Distributions Vol 2 Marcel Dekker New York ISBN 0 471 58494 0 Icsel kaynaklarIngilizce Vikipedia Logistic distribution maddesi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State