polinom kod, bir türüdür.
Tanım
Sabit bir 



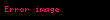

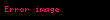

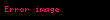
Örnek
GF(2) alanında 



veya açıkça şöyle yazılır:
Bu ifadenin ikili sayı sistemindeki eşdeğeri şöyledir:
Burada her polinom kodun, gerçekte bir doğrusal kod olduğuna dikkat edin. Yani kod sözcüğünün doğrusal kombinasyonları yine kod sözcüğüdür. Böyle bir durumda alan GF(2) olur. Doğrusal kombinasyonlar ikili sayı sisteminde XOR ile elde edilir. Örneğin; 00111 XOR 10010 = 10101.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
polinom kod bir turudur TanimSabit bir GF q displaystyle GF q sonlu alanindaki ogelere sembol denir Polinom kod elde edilmesindeki amac an 1 a0 displaystyle a n 1 ldots a 0 sembollerinden olusan bir n displaystyle n dizisinin polinomu soyledir an 1xn 1 a1x a0 displaystyle a n 1 x n 1 cdots a 1 x a 0 m n displaystyle m leq n sabit tam sayilar ve g x displaystyle g x m displaystyle m dereceden sabit polinom olsun Buna uretec polinom denir g x displaystyle g x ile uretilen polinom kod sozcukleri n displaystyle n den daha kucuk dereceli polinom olan ve g x displaystyle g x tarafindan kalansiz bolunebilir koddur OrnekGF 2 alaninda GF 2 0 1 displaystyle GF 2 0 1 n 5 displaystyle n 5 m 2 displaystyle m 2 ve uretec polinomu g x x2 x 1 displaystyle g x x 2 x 1 olsun Bu kod asagidaki kod sozcuklerinden olusur 0 g x 1 g x x g x x 1 g x displaystyle 0 cdot g x quad 1 cdot g x quad x cdot g x quad x 1 cdot g x x2 g x x2 1 g x x2 x g x x2 x 1 g x displaystyle x 2 cdot g x quad x 2 1 cdot g x quad x 2 x cdot g x quad x 2 x 1 cdot g x veya acikca soyle yazilir 0 x2 x 1 x3 x2 x x3 1 displaystyle 0 quad x 2 x 1 quad x 3 x 2 x quad x 3 1 x4 x3 x2 x4 x3 x 1 x4 x x4 x2 1 displaystyle x 4 x 3 x 2 quad x 4 x 3 x 1 quad x 4 x quad x 4 x 2 1 Bu ifadenin ikili sayi sistemindeki esdegeri soyledir 00000 00111 01110 01001 displaystyle 00000 quad 00111 quad 01110 quad 01001 11100 11011 10010 10101 displaystyle 11100 quad 11011 quad 10010 quad 10101 Burada her polinom kodun gercekte bir dogrusal kod olduguna dikkat edin Yani kod sozcugunun dogrusal kombinasyonlari yine kod sozcugudur Boyle bir durumda alan GF 2 olur Dogrusal kombinasyonlar ikili sayi sisteminde XOR ile elde edilir Ornegin 00111 XOR 10010 10101
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans






