Direnç - kapasitör devresi (RC devresi) veya RC filtresi direnç ve kapsitörlerden oluşan ve gerilim veya tarafından beslenen bir elektrik devresidir.
Başlangıç
Üç temel, doğrusal (lineer) analog devre elemanı vardır: direnç (R), kapasitör (C) ve bobin (L). Bunların dört önemli kombinasyonu vardır: RC devresi, , ve RLC devresi olarak bilinirler. Bu devreler, analog elektroniğin en önemli devrelerini oluşturur. Özellikle, (pasif filtrelerde) çokça kullanılır. Burada RC devresinin hem hem de diyagramları gösteriliyor.
Karmaşık empedans
Bir kapasitörün kapasitansı C (farad) ise ZC (ohm)
dir.
s açısal frekans gösterir ve genellikle bir karmaşık sayıdır,
Burada
- j sanal (imajiner) birimi gösterir:
gerçek (reel) kısım ve
sanal kısım, yani sinüzoidal olan açısal frekans (radyan/saniye)tır.
Seri devre

Devrede kapasitör üzerindeki gerilim:
ve direnç üzerindeki gerilim:
dir.
Transfer fonksiyonları
Kapasitörün transfer fonksiyonu
ve aynı şekilde direncin transfer fonfsiyonu
dir.
Kutuplar ve sıfırlar
Her iki transfer fonksiyonunda da tek kutup vardır.
.
Ek olarak, direnç için orijinde sıfır vardır.
Kazanç ve faz açısı
Kazanç iki etkene bağlıdır: Biri
diğeri ise
dir
ve faz açıları:
ve
.
Bu ifadeler birlikte kullanılabilir ve genellikle çıkışı temsil eder:
.
Akım
Seri devrelerde akım her yerde aynıdır:
İmpuls cevabı
Her gerilim için transfer fonksiyonunun karşılığı olan ters Laplace dönüşümüdür. Bu devre bir darbenin veya cevabının bir giriş gerilimine bağlı olduğunu gösterir.
Kapasitörün gerilimi için impuls cevabı
Burada u(t) ve
Aynı şekilde direnç geriliminin impuls cevabı
Burada da δ(t) Dirac delta fonksiyonudur.
Frekans uzayı faktörleri

olur.
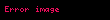
olur.
.
Yukarıdaki denklemin çözümünden şu sonuç elde edilir:
veya
Bu da filtrenin orijinal gücün yarısına düşeceği frekansıdır.
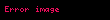
.

Zaman uzayı faktörleri
Zaman uzayını en doğru şekilde elde etmek için Laplace dönüşümünü ifade eden yukarıdaki 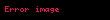
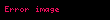
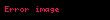
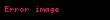

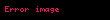
ve
.


açılımları ve ters Laplace dönüşümüü:
.
Bu eşitlikler kapasitör ve direnç üzerindeki gerilimleri sırasıyla hesaplamak içindir. Kapasitörün sırasındaki eşitlikler; sırasındaki eşitliklerin tam tersidir. Bu eşitlikler şarj ve akım ilişkisi C=Q/V ve V=IR (Ohm Kanununa bakın) kullanılarak tekrar yazılabilir.
Bu eşitlikler seri RC devrelerinde bir olduğunu gösteriyor, genellikle 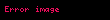


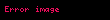
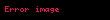
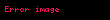
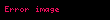
Değişim oranı her 
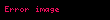
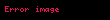
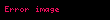
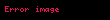

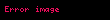


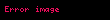

Ayrıca çözümü ile elde edilebilen bu sonuçlar devreyi tanımlayabilir:
ve
.
İlk denklem bir kullanılarak ve ikincisi takiben kolayca çözülür; çözümler böylece Laplace dönüşümleri yoluyla tam aynısı olarak elde edilir.
İntegral işlemi
yüksek frekanstada kapasitör karşısında çıkış düşünülür yani.
.
Bunun anlamı bu kapasitörün dolmasına zaman yetersizdir ve böylece bu voltaj çok küçüktür. Böylece direnç karşısında voltaj yaklaşık giriş voltajına eşittir. 
ama unutmadan frekans durumu şu şekilde tanımlanır
böylece
bu sadece Ohm kanunu'dur
Şimdi,
böylece
,
bu kapasitörün karşısında bir 'dür
Türev işlemi
düşük frekansta çıkış karşısında düşünüldüğünde; yani,
.
Bunun anlamı bu kapasitör voltajı kadar yukarı şarja zaman var ve voltaj kaynağına neredeyse eşittir. 
,
böylece
Şimdi,
bu bir karşısında dirençtir.
Daha kesin integrasyon ve giriş üzerinde uygun olarak dirençleri ve kapasitörler yerleştirerek ve döngü geribeslemesi sağlanabilir.
Paralel devre

Paralel RC devresi genellikle seri devreden daha az ilgi görür. Çünkü çıkış gerilimi 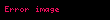
Karmaşık empedans:
ve
.
Bu kapasitör akımının 90° olduğunu gösteriyor.direnç(ve kaynak) akımı ile fazın çıkışı. Karşıt olarak, diferansiyel denklemler kullanılarak yönetiliyor:
ve
.
Bir basamak giriş için (bu etkili bir 0 Hz veya işaretidir), girişin türevi 
Bakınız
Dış bağlantılar
- RC Filter Calculator14 Temmuz 2011 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Direnc kapasitor devresi RC devresi veya RC filtresi direnc ve kapsitorlerden olusan ve gerilim veya tarafindan beslenen bir elektrik devresidir BaslangicUc temel dogrusal lineer analog devre elemani vardir direnc R kapasitor C ve bobin L Bunlarin dort onemli kombinasyonu vardir RC devresi ve RLC devresi olarak bilinirler Bu devreler analog elektronigin en onemli devrelerini olusturur Ozellikle pasif filtrelerde cokca kullanilir Burada RC devresinin hem hem de diyagramlari gosteriliyor Karmasik empedansBir kapasitorun kapasitansi C farad ise ZC ohm ZC 1sC displaystyle Z C frac 1 sC dir s acisal frekans gosterir ve genellikle bir karmasik sayidir s s jw displaystyle s sigma j omega Burada j sanal imajiner birimi gosterir j2 1 displaystyle j 2 1 s displaystyle sigma gercek reel kisim ve w displaystyle omega sanal kisim yani sinuzoidal olan acisal frekans radyan saniye tir Seri devreRC devresi Devrede kapasitor uzerindeki gerilim VC s 1 CsR 1 CsVin s 11 RCsVin s displaystyle V C s frac 1 Cs R 1 Cs V in s frac 1 1 RCs V in s ve direnc uzerindeki gerilim VR s RR 1 CsVin s RCs1 RCsVin s displaystyle V R s frac R R 1 Cs V in s frac RCs 1 RCs V in s dir Transfer fonksiyonlari Kapasitorun transfer fonksiyonu HC s VC s Vin s 11 RCs displaystyle H C s V C s over V in s 1 over 1 RCs ve ayni sekilde direncin transfer fonfsiyonu HR s VR s Vin s RCs1 RCs displaystyle H R s V R s over V in s RCs over 1 RCs dir Kutuplar ve sifirlar Her iki transfer fonksiyonunda da tek kutup vardir s 1RC displaystyle s 1 over RC Ek olarak direnc icin orijinde sifir vardir Kazanc ve faz acisi Kazanc iki etkene baglidir Biri GC HC jw VC jw Vin jw 11 wRC 2 displaystyle G C H C j omega left frac V C j omega V in j omega right frac 1 sqrt 1 left omega RC right 2 digeri ise GR HR jw VR jw Vin jw wRC1 wRC 2 displaystyle G R H R j omega left frac V R j omega V in j omega right frac omega RC sqrt 1 left omega RC right 2 dir ve faz acilari ϕC HC jw tan 1 wRC displaystyle phi C angle H C j omega tan 1 left omega RC right ve ϕR HR jw tan 1 1wRC displaystyle phi R angle H R j omega tan 1 left frac 1 omega RC right Bu ifadeler birlikte kullanilabilir ve genellikle cikisi temsil eder VC GCVinejϕC displaystyle V C G C V in e j phi C VR GRVinejϕR displaystyle V R G R V in e j phi R Akim Seri devrelerde akim her yerde aynidir I s Vin s R 1 Cs Cs1 RCsVin s displaystyle I s frac V in s R 1 Cs Cs over 1 RCs V in s Impuls cevabi Her gerilim icin transfer fonksiyonunun karsiligi olan ters Laplace donusumudur Bu devre bir darbenin veya cevabinin bir giris gerilimine bagli oldugunu gosterir Kapasitorun gerilimi icin impuls cevabi hC t 1RCe t RCu t 1te t tu t displaystyle h C t 1 over RC e t RC u t 1 over tau e t tau u t Burada u t ve t RC displaystyle tau RC zaman sabitidir Ayni sekilde direnc geriliminin impuls cevabi hR t d t 1RCe t RCu t d t 1te t tu t displaystyle h R t delta t 1 over RC e t RC u t delta t 1 over tau e t tau u t Burada da d t Dirac delta fonksiyonudur Frekans uzayi faktorleri w displaystyle omega to infty a yaklastikca GC 0 displaystyle G C to 0 GR 1 displaystyle G R to 1 olur w 0 displaystyle omega to 0 a yaklastikca GC 1 displaystyle G C to 1 GR 0 displaystyle G R to 0 olur GC GR 12 displaystyle G C G R frac 1 sqrt 2 Yukaridaki denklemin cozumunden su sonuc elde edilir wc 1RC rad s displaystyle omega c frac 1 RC mathrm rad s veya fc 12pRC Hz displaystyle f c frac 1 2 pi RC mathrm Hz Bu da filtrenin orijinal gucun yarisina dusecegi frekansidir w 0 displaystyle omega to 0 a yaklastikca ϕC 0 displaystyle phi C to 0 ϕR 90 p 2c displaystyle phi R to 90 circ pi 2 c w displaystyle omega to infty a yaklastikca ϕC 90 p 2c displaystyle phi C to 90 circ pi 2 c ϕR 0 displaystyle phi R to 0 Zaman uzayi faktorleri Zaman uzayini en dogru sekilde elde etmek icin Laplace donusumunu ifade eden yukaridaki VC displaystyle V C ve VR displaystyle V R yapilari kullanilir Bu etkin donusumler jw s displaystyle j omega s e donusturulur yaklasimi yapilir orn Once Vin 0 displaystyle V in 0 yapilarak t 0 displaystyle t 0 bulunur sonra Vin V displaystyle V in V yapilir Vin s V1s displaystyle V in s V frac 1 s VC s V11 sRC1s displaystyle V C s V frac 1 1 sRC frac 1 s ve VR s VsRC1 sRC1s displaystyle V R s V frac sRC 1 sRC frac 1 s Kapasitor geriliminin adim cevabi Direnc geriliminin adim cavabi acilimlari ve ters Laplace donusumuu VC t V 1 e t RC displaystyle V C t V left 1 e t RC right VR t Ve t RC displaystyle V R t Ve t RC Bu esitlikler kapasitor ve direnc uzerindeki gerilimleri sirasiyla hesaplamak icindir Kapasitorun sirasindaki esitlikler sirasindaki esitliklerin tam tersidir Bu esitlikler sarj ve akim iliskisi C Q V ve V IR Ohm Kanununa bakin kullanilarak tekrar yazilabilir Bu esitlikler seri RC devrelerinde bir oldugunu gosteriyor genellikle t RC displaystyle tau RC ifadesi voltaj karsisinda bilesenleri ya C karsisinda ya yukselir veya R karsisinda bu son degerin 1 e displaystyle 1 e ye birlikte duser Boylece t displaystyle tau zamaninda V 1 1 e displaystyle V 1 1 e VC displaystyle V C ye ve V 1 e displaystyle V 1 e VR displaystyle V R ye ulasabilir Degisim orani her t displaystyle tau bir fraksiyonel 1 1e displaystyle left 1 frac 1 e right dir Boylece t Nt displaystyle t N tau dan t N 1 t displaystyle t N 1 tau ye icinde giden voltaj bu seviyeden yolun yaklasik 63 2 si tasinacak t Nt displaystyle t N tau de yonunde bu sonuc degerdir Boylece C t displaystyle tau sonrasinda yaklasik 63 2 ye dolacak ve yaklasik 5t displaystyle 5 tau sonrasinda aslinda tam dolacak 99 3 Eger voltaj kaynagi bir kisa devre ile yerdegistirirse C 0 yonunde V displaystyle V den t ile C karsisinda voltaj C tam yuku ile ustel sekilde damlar C t displaystyle tau sonrasinda yaklasik 36 8 ye dusmus ve aslinda 5t displaystyle 5 tau sonrasinda aslinda tamamen bosalmis 0 7 olacak Unutmadan I displaystyle I akimi Ohm Kanunu yoluyla R karsisinda voltaj olarak akim davranisi icinde bunu yapar Ayrica cozumu ile elde edilebilen bu sonuclar devreyi tanimlayabilir Vin VCR CdVCdt displaystyle frac V in V C R C frac dV C dt ve VR Vin VC displaystyle V R V in V C Ilk denklem bir kullanilarak ve ikincisi takiben kolayca cozulur cozumler boylece Laplace donusumleri yoluyla tam aynisi olarak elde edilir Integral islemi yuksek frekanstada kapasitor karsisinda cikis dusunulur yani w 1RC displaystyle omega gg frac 1 RC Bunun anlami bu kapasitorun dolmasina zaman yetersizdir ve boylece bu voltaj cok kucuktur Boylece direnc karsisinda voltaj yaklasik giris voltajina esittir I displaystyle I icin yukarida verilen baginti dusunuldugunde suna bakalim I VinR 1 jwC displaystyle I frac V in R 1 j omega C ama unutmadan frekans durumu su sekilde tanimlanir wC 1R displaystyle omega C gg frac 1 R boylece I VinR displaystyle I approx frac V in R bu sadece Ohm kanunu dur Simdi VC 1C 0tIdt displaystyle V C frac 1 C int 0 t Idt boylece VC 1RC 0tVindt displaystyle V C approx frac 1 RC int 0 t V in dt bu kapasitorun karsisindabir dur Turev islemi dusuk frekansta cikis karsisinda dusunuldugunde yani w 1RC displaystyle omega ll frac 1 RC Bunun anlami bu kapasitor voltaji kadar yukari sarja zaman var ve voltaj kaynagina neredeyse esittir I displaystyle I icin yine baginti dusunuldugunde o zaman R 1wC displaystyle R ll frac 1 omega C boylece I Vin1 jwC displaystyle I approx frac V in 1 j omega C Vin IjwC VC displaystyle V in approx frac I j omega C approx V C Simdi VR IR CdVCdtR displaystyle V R IR C frac dV C dt R VR RCdVindt displaystyle V R approx RC frac dV in dt bu bir karsisinda direnctir Daha kesin integrasyon ve giris uzerinde uygun olarak direncleri ve kapasitorler yerlestirerek ve dongu geribeslemesi saglanabilir Paralel devreRC devresi Paralel RC devresi genellikle seri devreden daha az ilgi gorur Cunku cikis gerilimi Vout displaystyle V out giris gerilimi olan Vin displaystyle V in e esittir Sonuc olarak bu devre bir tarafindan beslenen bir filtre degildir Karmasik empedans IR VinR displaystyle I R frac V in R ve IC jwCVin displaystyle I C j omega CV in Bu kapasitor akiminin 90 oldugunu gosteriyor direnc ve kaynak akimi ile fazin cikisi Karsit olarak diferansiyel denklemler kullanilarak yonetiliyor IR VinR displaystyle I R frac V in R ve IC CdVindt displaystyle I C C frac dV in dt Bir basamak giris icin bu etkili bir 0 Hz veya isaretidir girisin turevi t 0 displaystyle t 0 da bir Boylece kapasitor cok hizli tam yuke ulasir ve bir olur boylece bir kapasitorun DC davranisi iyi bilinir BakinizDis baglantilarRC Filter Calculator14 Temmuz 2011 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State