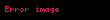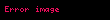Sıra teorisi, kullanma sırasının sezgisel kavramını inceleyen bir matematik dalıdır. "Bu, şundan daha küçüktür" veya "bu, şundan daha öncedir" gibi durumları inceler.
Örneksel yaklaşım
Bir küme ve o küme üzerinde aşağıda tarif edilecek olan ikili bir bağıntıyı içeren aksiyomatik sistemlere denir. Bilinen sıralama 
- X kümesinin her a elemanı için R(a,a) bağıntısı sağlanmalıdır. (
şeklinde düşünülebilir, yansıma özelliği olarak bilinir.)
- X kümesinin herhangi iki a ve b elemanı için R(a, b) ve R(b,a) bağıntıları sağlanıyorsa,
olmalıdır. (hem
hem de
sağlanıyorsa a=b dir diye düşünülebilir, antisimetrik olma özelliği olarak bilinir.)
- X kümesinin herhangi üç a, b ve c elemanı için hem R(a, b) hem de R(b,c) bağıntıları sağlanıyorsa, o zaman R(a,c) bağıntısı da sağlanmalıdır. (hem
hem de
ise
de olmalıdır diye de düşünülebilir, geçişkenlik özelliği olarak bilinir)
Sıralamalara örnekler
(Doğal sayılar, 



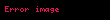
Sıralama çeşitleri
- Eğer elimizdeki sıralama nesnesi, yukardaki aksiyomlara ek başka varsayımlar sağlamıyorsa elimizdeki sıralamaya "kısmi sıralama" denir. Yani her sıralama bir kısmi sıralamadır.
- Eğer yukardaki aksiyomlara ek olarak X ten seçeceğimiz herhangi iki elemanı karşılaştırabiliyorsak (yani R(a, b) ve R(b,a) bağıntılarından biri mutlaka doğru olmak zorundaysa) o zaman elimizdeki sıralamaya doğrusal sıralama denir. Yukardaki örneklerden (Doğal Sayılar,
), (Rasyonel Sayılar,
) ve (Reel Sayılar,
) aynı zamanda doğrusal sıralamalara da örneklerken, (Kümeler Uzayı,
bağıntısı), doğrusal olmayan kısmi bir sıralamadır. Nedeni herhangi iki kümeyi
bağıntısına göre karşılaştırmanın mümkün olmamasıdır. Yani biri diğerini içermeyen iki kümenin varlığıdır.
- Son olarak, doğrusal sıralama şartlarını sağlayan (X, R) sıralamalarından, "X in her alt kümesinin bir en küçük eleman içermesi şartı"nı sağlayanlara iyi-sıralama denir. Yukarıdaki örneklerden reel sayılar ve doğal sayılar iyi-sıralama iken, rasyonel sayılar iyi sıralama değildir. Örnek olarak "karekök ikiden büyük rasyonel sayılar" kümesinin en küçük bir elemanı olmaması verilebilir.
Sıralamaların önemi
- Her sıralama nesnesi bir topolojik uzay yapısına sahiptir. Bu yapının açık kümelerinin temeli "öyle x elemanları ki
" şeklinde ifade edilebilen kümelerden oluşur, a veya b az önceki formülde gözükmüyor da olabilirler.
- , sayesinde kısmi sıralamalar matematiğin pek çok alanında uygulama bulmuşlardır. Mesela halka'larda maksimal varlığı Zorn'un Lemması ve ideallarin
bağıntısına göre kısmi bir sıralama oluşturduğu gerçeği kullanılarak ispatlanır.
- Reel sayılar kümesinin rasyonel sayılar kümesini kullanılarak oluşturulmasının bir temeli de Alman matematikçi Richard Dedekind tarafından verilmiştir. Dedekind'in yöntemi rasyonel sayılar kümesinin bir iyi-sıralama haline getirilmesine dayanır. Diğer yöntem ise "bütünleme"dir.
- İyi sıralamar matematikte nispeten nadir gözlenen, çok güçlü özellikler içeren objelerdir. Bu ilke ve kümeler teorisi arasındaki ilişki hakkında bilgi için ayrica İyi-sıralılık ilkesi Makalesi'ne bakabilirsiniz.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Sira teorisi kullanma sirasinin sezgisel kavramini inceleyen bir matematik dalidir Bu sundan daha kucuktur veya bu sundan daha oncedir gibi durumlari inceler Orneksel yaklasimBir kume ve o kume uzerinde asagida tarif edilecek olan ikili bir bagintiyi iceren aksiyomatik sistemlere denir Bilinen siralama displaystyle leq bagintisinin soyutlanmasiyla elde edilirler Kumemize X bagintimiza R adini verecek olursak asagidaki aksiyomlarin saglandigini varsayariz X kumesinin her a elemani icin R a a bagintisi saglanmalidir a a displaystyle a leq a seklinde dusunulebilir yansima ozelligi olarak bilinir X kumesinin herhangi iki a ve b elemani icin R a b ve R b a bagintilari saglaniyorsa a b displaystyle a b olmalidir hem a b displaystyle a leq b hem de b a displaystyle b leq a saglaniyorsa a b dir diye dusunulebilir antisimetrik olma ozelligi olarak bilinir X kumesinin herhangi uc a b ve c elemani icin hem R a b hem de R b c bagintilari saglaniyorsa o zaman R a c bagintisi da saglanmalidir hem a b displaystyle a leq b hem de b c displaystyle b leq c ise a c displaystyle a leq c de olmalidir diye de dusunulebilir geciskenlik ozelligi olarak bilinir Siralamalara ornekler Dogal sayilar displaystyle leq bagintisi Rasyonel sayilar displaystyle leq bagintisi Reel sayilar displaystyle leq bagintisi Kumeler Uzayi displaystyle subset bagintisi displaystyle Teknik olarak bir kume degildir Ancak bu sorun yaratmaz Siralama cesitleriEger elimizdeki siralama nesnesi yukardaki aksiyomlara ek baska varsayimlar saglamiyorsa elimizdeki siralamaya kismi siralama denir Yani her siralama bir kismi siralamadir Eger yukardaki aksiyomlara ek olarak X ten sececegimiz herhangi iki elemani karsilastirabiliyorsak yani R a b ve R b a bagintilarindan biri mutlaka dogru olmak zorundaysa o zaman elimizdeki siralamaya dogrusal siralama denir Yukardaki orneklerden Dogal Sayilar displaystyle leq Rasyonel Sayilar displaystyle leq ve Reel Sayilar displaystyle leq ayni zamanda dogrusal siralamalara da orneklerken Kumeler Uzayi displaystyle subset bagintisi dogrusal olmayan kismi bir siralamadir Nedeni herhangi iki kumeyi displaystyle subset bagintisina gore karsilastirmanin mumkun olmamasidir Yani biri digerini icermeyen iki kumenin varligidir Son olarak dogrusal siralama sartlarini saglayan X R siralamalarindan X in her alt kumesinin bir en kucuk eleman icermesi sarti ni saglayanlara iyi siralama denir Yukaridaki orneklerden reel sayilar ve dogal sayilar iyi siralama iken rasyonel sayilar iyi siralama degildir Ornek olarak karekok ikiden buyuk rasyonel sayilar kumesinin en kucuk bir elemani olmamasi verilebilir Siralamalarin onemiHer siralama nesnesi bir topolojik uzay yapisina sahiptir Bu yapinin acik kumelerinin temeli oyle x elemanlari ki a x b displaystyle a leq x leq b seklinde ifade edilebilen kumelerden olusur a veya b az onceki formulde gozukmuyor da olabilirler sayesinde kismi siralamalar matematigin pek cok alaninda uygulama bulmuslardir Mesela halka larda maksimal varligi Zorn un Lemmasi ve ideallarin displaystyle subset bagintisina gore kismi bir siralama olusturdugu gercegi kullanilarak ispatlanir Reel sayilar kumesinin rasyonel sayilar kumesini kullanilarak olusturulmasinin bir temeli de Alman matematikci Richard Dedekind tarafindan verilmistir Dedekind in yontemi rasyonel sayilar kumesinin bir iyi siralama haline getirilmesine dayanir Diger yontem ise butunleme dir Iyi siralamar matematikte nispeten nadir gozlenen cok guclu ozellikler iceren objelerdir Bu ilke ve kumeler teorisi arasindaki iliski hakkinda bilgi icin ayrica Iyi siralilik ilkesi Makalesi ne bakabilirsiniz
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans