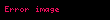Azərbaycanca
Беларускі
Dansk
Deutsch
Española
Français
Indonesia
Italiana
日本語
Қазақ
Lietuvos
Nederlands
Português
Русский
සිංහල
แบบไทย
Türkçe
Українська
中國人
United State
Afrikaans
Taşınım olayı (veya taşınım fenomeni), mühendislik, fizik ve kimyada gözlemlenen ve üzerine araştırma gerçekleştirilen sistemlerin, kütle, enerji, yük, momentum ve açısal momentum değişimiyle ilgilenen çalışmalardır. Sürekli ortamlar mekaniği ve termodinamik gibi pek çok farklı alandan yararlanırken, ele aldığı konular üzerindeki ortaklıklara önemli düzeyde vurgu yapmaktadır.
Kütle, momentum ve ısı aktarımı olayları oldukça benzer bir matematiksel temele sahiptirler. Taşınım olayı çalışmalarında, doğrudan diğerlerinden türetilen alanların analizinde oldukça kullanışlı ve derinlikli matematiksel bağlantılar kurmakta bu benzer temellerden faydalanılır.
Üç alt ana dal olan kütle, ısı ve momentum aktarımının temel analizi, genellikle incelenen büyüklüklerin toplamının, sistem ve çevresi tarafından korunması gerektiği ilkesine dayanmaktadır. Bu nedenle taşınıma sebep olan her olay, katkılarının toplamının sıfıra eşit olacağı bilgisiyle ayrı ayrı ele alınırlar. Bu ilke, ilgili pek çok büyüklüğün hesaplanmasında kullanışlıdır. Örneğin sabit bir hacim boyunca akan bir akışkanın belirlenmesi, akışkanlar mekaniğinde sıkça rastlanan bir taşınım analizidir.
Taşınım olayı mühendislik disiplinlerinin her yerinde bulunmaktadır. Taşınım analizinin en yaygın örnekleri proses, kimya ve makine mühendisliği ile biyomühendislik alanlarında görülür ancak akışkanlar mekaniği, ısı aktarımı ve kütle aktarımı ile uzaktan veya yakından ilintili tüm disiplinlerin müfredatında temel bir unsurdur. Taşınım olayı günümüzde en az termodinamik, mekanik ve elektromanyetizma kadar mühendislik disiplininin bir parçası olarak kabul edilmektedir.
Taşınım olayları evrendeki tüm fiziksel değişim etkenlerini kapsamaktadır. Dahası, evreni oluşturan ve dünya üzerindeki tüm yaşamın başarısından sorumlu temel yapı taşlarından biri olarak kabul edilmektedir. Ancak burada verilen bilgilerin kapsamı, taşınım olaylarının yapay mühendislik sistemleri ile ilişkisiyle sınırlıdır.
Genel bakış
Fizikte taşınım olaylarının hepsi, çoğunlukla akışkanlarda gözlemlenen, moleküllerin sürekli ve rastgele hareketlerinden kaynaklanan istatistiksel doğanın . Taşınım olaylarının tüm unsurları, ve olmak üzere iki temel kavrama dayalıdır: Taşınım olaylarının içeriğinde bulunan korunum yasaları, söz konusu büyüklüğün nasıl korunacağını tanımlayan halinde formüle edilir. Temel eşitlikler ise söz konusu büyüklüğün çeşitli etkenlere taşınım yoluyla nasıl tepki verdiğini tanımlar. Buna önemli örnekler arasında Fourier'in Isı İletim Kanunu ve Navier-Stokes denklemleri vardır. Fourier kanunu, ısı akısının sıcaklık gradyanına verdiği tepkiyi tanımlarken, Navier-Stokes eşitlikleri de akışkan akısı ve akışkana uygulanan kuvvetler arasındaki ilişkiyi açıklar. Bu eşitlikler aynı zamanda taşınım olayları ve termodinamik arasındaki derin bağlantıyı, yani taşınım olaylarının neden geri dönüşümsüz olduğunu açıklayan bağlantıyı ortaya koymaktadır. Bu fiziksel olayların neredeyse tamamı minimum enerji prensibine uygun olarak en düşük enerjili hâle geçmeye çalışan sistemleri kapsar. Sistemler bu hâle yaklaştıkça sürücü güçlerin sistemde artık yer almadığı ve taşınımda kesintinin olmadığı gerçek termodinamik dengeye ulaşma eğilimi gösterirler. Bu türde bir dengenin çeşitli yönleri doğrudan ısı aktarımına bağlıdır. Kütle ve momentum aktarımının sistemi kimyasal ve mekanik dengeye doğru hareket ettirmesine benzer olarak ısı aktarımı da sistemin çevresiyle ısıl dengeye ulaşmaya çalışmasıdır.
Isı iletimi (enerji aktarımı), akışkan akışı (momentum aktarımı), (kütle aktarımı), radyasyon ve yarı iletkenlerde elektrik yükü aktarımı taşınım süreçlerine birer örnektir.
Taşınım olaylarının geniş bir uygulama alanı vardır. Örneğin katı hâl fiziğinde elektronların, deliklerin ve fononların hareketi ve etkileşimleri "taşınım olayları" altında incelenir. Bir diğer örnek de biyomedikal mühendislikte ilgilenilen termoregülasyon, perfüzyon ve gibi taşınım olaylarıdır. Kimya mühendisliğinde taşınım olayları reaktör tasarımında, membran analizlerinde, moleküler veya difüzif taşınım mekanizmalarının analizinde ve metalurjide kullanılır.
Kütle, enerji ve momentum aktarımı dış kaynaklar sebebiyle etkilenebilir:
- Bir kokunun yayılma hızı, rüzgâr hızı, sıcaklık ve ortamın nemliliği gibi pek çok etkene bağlı olarak değişebilir. Örneğin çok güçlü esen bir rüzgâr bir kokuyu hafif bir esintiye göre çok daha uzaklara hızlı bir şekilde taşıyabilir.
- Isı iletebilen bir katının soğuma hızı, bir ısı kaynağının varlığına bağlı olarak değişir.
- Bir yağmur damlasına etkiyen yerçekimi kuvveti, damlayı çevreleyen havanın uyguladığı direnci veya sürüklenmeyi etkisizleştirir.
Olaylar arasındaki ortaklıklar
Taşınım olayları çalışmalarındaki önemli bir ilke de olaylar arasındaki benzerliklerdir.
Difüzyon
Aşağıdaki örneklerde de gösterildiği üzere, hepsi de difüzyon yoluyla taşınabilen kütle, enerji ve momentum aktarımı denklemleri arasında önemli benzerlikler vardır:
- Kütle: Kokuların havada yayılması kütle difüzyonuna bir örnektir.
- Enerji: Katı bir malzemede ısı iletimi, ısı difüzyonuna bir örnektir.
- Momentum: Bir yağmur damlasının atmosfer boyunca düşerken uğradığı sürüklenme, bir örneğidir (yağmur damlasının momentumu viskoz gerilmeler sebebiyle onu çevreleyen havaya geçer ve damla yavaşlar).
Akışkan momentumu için Newton yasası, (Fourier'in ısı kanunu) ve moleküler taşınım denklemleri birbirine oldukça benzerdir. Üç farklı taşınım olayını birbirleriyle karşılaştırmak için bir taşınım katsayısından diğerine dönüşüm gerçekleştirilebilir.
| Taşınan büyüklük | Fiziksel olay | Eşitlik |
|---|---|---|
| Momentum | Viskozite (Newton tipi akışkan) |  |
| Enerji | Isı iletimi ((Fourier kanunu)) |  |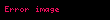
| Kütle | () |  |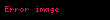
(Eşitliklerin tanımları aşağıda verilmiştir)
Literatürde türbülent taşınım için bu üç taşınım olayı arasında benzerlikler geliştirilerek birinin diğerinden tahmin edilebilmesini sağlamak için büyük çaba sarf edilmiştir. , türbülent difüzivitelerin eşit olduğunu ve moleküler kütle (D AB) ile momentum (μ/ρ) difüzivitelerinin türbülent difüzyonla karşılaştırıldığında ihmal edilebilir olduğunu varsayar. Sistemde sıvılar ve sürükleme birlikte veya ayrı ayrı mevcut ise, bu benzerlik geçerli değildir. Prandtl'ın ve von Karman'ınkiler gibi diğer benzerlikler de genellikle yetersiz bağıntılar vermektedir.
En başarılı ve en çok kullanılan benzerlik . Bu benzerlik gazlar ve sıvıların hem laminer hem türbülanslı akış rejimlerinde elde edilmiş deneysel veriler üzerine kuruludur. Deneysel verilere dayanmasına rağmen, düz bir plaka üzerindeki laminer akıştan elde edilmiş kesin çözümün doğrulanması için de kullanılabilir. Tüm bu veriler kütle aktarımını tahmin etmek için kullanılır.
Onsager ters bağıntıları
Sıcaklık, madde yoğunluğu ve basınç cinsinden tanımlanan akışkan sistemlerinde sıcaklık farklarının, sistemin sıcak kısmından soğuk kısımlarına ısı akışına yol açtığı bilinmektedir. Benzer şekilde, basınçtaki farklılıklar, maddenin yüksek basınçtan düşük basınçlı bölgelere ("ters bağıntı") akışına yol açacaktır. Sıcaklık ve basıncın değişebilir olduğu sistemlerde dikkat çekici olan şey, sabit basınçtayken sıcaklığın değişmesinin madde akışına (konveksiyonda olduğu gibi) ve sabit sıcaklıktayken basınç değişiminin ısı akışına neden olabileceği gözlemidir. Birim basınç farkı başına gerçekleşen ısı akışı ile birim sıcaklık farkı başına gerçekleşen madde akışı şaşırtıcı biçimde aynı olabilirdi.
Lars Onsager mikroskobik dinamiğin zaman tersinirliğinin bir sonucu olarak istatistiksel mekaniği kullanarak bu eşitliğin gerekli olduğunu göstermiştir. Onsager tarafından geliştirilen teori verilen örneklerden çok daha geneldir ve aynı anda ikiden fazla termodinamik kuvveti işleme tabi tutabilir.
Momentum aktarımı
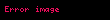ifadesi ile gösterilir.Momentum aktarımında, üzerinde çalışma yapılan akışkan, maddenin sürekli bir dağılımı olarak kabul edilir. Momentum aktarımı ya da akışkanlar mekaniği, akışkanlar statiği (hareketsiz akışkanlar) ve akışkanlar dinamiği (hareket halindeki akışkanlar) olmak üzere iki dala ayrılır. Bir akışkan katı bir yüzeye paralel x yönünde akarken, momentumu x yönünde ve konsantrasyonu υxρ olur. Moleküllerin rastgele difüzyonundan dolayı x yönünde dik olan y yönünde bir molekül değişimi vardır. Bu nedenle x yönüne akıştaki momentum, y yönü boyunca hızlı hareket eden katmandan yavaş hareket eden katmana doğru aktarılır. Yani momentum x yönü boyunca sabitken, y yönünde, yani akışkanın katmanları boyunca değişir. Buna dayalı olarak momentum aktarım denklemi olan Newton'un Viskozite Kanunu aşağıdaki gibi yazılır:
Burada τxy, x yönünde akan akışkanın y yönü boyunca oluşan kayma gerilmesidir. Momentum akısı olarak da adlandırılır. ν kinematik viskozitedir ve μ/ρ olarak da ifade edilir. y taşınım veya difüzyonun gerçekleştiği mesafedir. ρ yoğunluk ve μ da dinamik viskozitedir. Newton Yasası, momentum akısı ile hız gradyanı arasındaki en basit ilişkidir.
Kütle aktarımı
Bir sistemde derişim bir noktadan başka bir noktaya değişiyorsa, kütlenin sistemdeki derişim farkını en aza indirecek şekilde taşınımına doğal bir eğilim bulunmaktadır. Bir sistemdeki kütle aktarımı Birinci Fick Kanunu ile belirlenir:
"Yüksek derişimden düşük derişime gerçekleşen difüzyonun akısı, ortamdaki maddenin derişim gradyanı ve difüzivitesi ile orantılıdır."
Kütle aktarımı farklı itici güçler yoluyla gerçekleşebilir. Bunlardan bazıları:
- Kütle, bir basınç gradyanının etkisiyle aktarılabilir (basınç difüzyonu).
- Bazı dış kuvvetlerin etkisiyle zorlanmış difüzyon oluşabilir.
- Sıcaklık gradyanlarından ötürü difüzyon gerçekleşebilir (termal difüzyon).
- farklardan dolayı difüzyon gerçekleşebilir.
A ve B'den oluşan bir karışımda A'nın difüzyonu, aşağıda verilen Fick'in Difüzyon Kanunu ile belirlenir:
Burada DAB difüzyon katsayısı, x difüzyon yönü, JAx A maddesinin x yönü boyunca molar difüzyon hızı, Ca ise A'nın derişimidir.
Enerji aktarımı
Mühendislikteki tüm süreçlerde enerji aktarımı bulunmaktadır. Buna örnek olarak proses akımlarının ısıtılması ve soğutulması, hâl değişimleri, distilasyon ve benzeri işlemler verilebilir. Temel ilke, bir statik sistem için aşağıdaki gibi ifade edilmiş olan termodinamiğin ilk kanunudur:
Bir sistem boyunca net enerji akışı (q), ısı iletim katsayısı (k) ve sıcaklığın mekâna göre değişim hızının (dT/dx) çarpımına eşittir. Isı iletim katsayısı ve enerji akışının birimlerine bağlı olarak bu denkleme kesit yüzey alanı da (A) eklenebilir.
Türbülanslı akış, karmaşık geometriler veya işlem yapılması zor sınır koşulları içeren diğer sistemler için başka bir denklemin kullanımı daha kolay olacaktır. Bu denklem ısı taşınım (konveksiyon) denklemidir:
Burada A yüzey alanı, 
ısı aktarımına sebep olan sıcaklık farkı, Q birim zamanda aktarılan ısı miktarı ve h de ısı iletim katsayısıdır.
Isı aktarımında iki tür taşınım (konveksiyon) gerçekleşebilir:
- (veya zorlanmış konveksiyon): hem laminer hem de türbülanslı akışta gerçekleşebilir. Dairesel borularda laminer akışın gerçekleştiği durumlarda, Nusselt sayısı, Reynolds sayısı ve Prandtl sayısı gibi çeşitli boyutsuz sayılar kullanılmaktadır. Yaygın olarak kullanılan denklem aşağıdaki gibidir:
- (veya konveksiyon) Grashof ve Prandtl sayılarının bir fonksiyonudur. Doğal konveksiyon ile ısı transferinin karmaşıklığı, deneysel verilerden türetilen ampirik ilişkilerin kullanılmasını gerekli kılmaktadır.
Isı aktarımı, , nükleer reaktörler, kimyasal reaktörler ve ısı değiştiriciler gibi endüstriyel ekipmanlarda analiz edilmektedir.
Uygulamalar
Kirlilik
Taşınım süreçlerinin araştırılması, kirleticilerin çevreye salınımı ve yayılımının anlaşılabilmesi için önemlidir. Doğru bir modelleme kirlilik azaltma stratejilerinin belirlenmesine özellikle yardımcı olabilir. Kentsel akıştan kaynaklı su yüzeyi kirliliğinin kontrolü ve ABD'deki araçların fren balatalarının bakır içeriğini azaltmayı amaçlayan politikalar gibi nice çalışma, taşınım olayları uygulamalarına birer örnek olarak verilebilir.
Ayrıca bakınız
Kaynakça
- ^ Truskey, George; Yuan F; Katz D. (2009). Transport Phenomena in Biological Systems (Second ed.) (İngilizce). s. 888. ISBN .
- ^ Transport phenomena fundamentals (Chemical Industries Series). CRC Press. Nisan 2001. ss. 1, 2, 3. ISBN . 7 Eylül 2014 tarihinde kaynağından . Erişim tarihi: 20 Haziran 2020.
- ^ Plawsky, Joel., "Transport Phenomena Fundamentals." Marcel Dekker Inc.,2009
- ^ Alonso & Finn. "Physics." Addison Wesley,1992. Chapter 18
- ^ Deen, William M. "Analysis of Transport Phenomena." Oxford University Press. 1998
- ^ J. M. Ziman, Electrons and Phonons: The Theory of Transport Phenomena in Solids (Oxford Classic Texts in the Physical Sciences)
- ^ Griswold, S. S. (1962). Air Pollution Control Field Operations Manual: A Guide for Inspection and Enforcement (İngilizce). U.S. Department of Health, Education and Welfare. ss. 203-204. 22 Haziran 2020 tarihinde kaynağından . Erişim tarihi: 20 Haziran 2020.
- ^ Welty, James R.; Wicks, Charles E.; Wilson, Robert Elliott (1976). Fundamentals of momentum, heat, and mass transfer (2 bas.). Wiley. 3 Ağustos 2020 tarihinde kaynağından . Erişim tarihi: 20 Haziran 2020.
- ^ "Thomas, William J. "Introduction to Transport Phenomena." Prentice Hall: Upper Saddle River, NJ, 2000.
- ^ Transport Phenomena (1 bas.). Nirali Prakashan. 2006. s. 15–3. ISBN . 19 Ağustos 2020 tarihinde kaynağından . Erişim tarihi: 20 Haziran 2020., Chapter 15, p. 15-3 19 Ağustos 2020 tarihinde Wayback Machine sitesinde .
- ^ Onsager (15 Şubat 1931). "Reciprocal Relations in Irreversible Processes. I." Physical Review. American Physical Society (APS). 37 (4): 405-426.
- ^ a b "Griskey, Richard G. "Transport Phenomena and Unit Operations." Wiley & Sons: Hoboken, 2006. 228-248.
- ^ Müller (20 Mart 2020). "The pollution conveyed by urban runoff: A review of sources". Science of the Total Environment (İngilizce). 709: 136125. 21 Haziran 2020 tarihinde kaynağından . Erişim tarihi: 20 Haziran 2020.
- ^ "Copper-Free Brake Initiative". US EPA (İngilizce). 10 Kasım 2015. 29 Aralık 2015 tarihinde kaynağından . Erişim tarihi: 1 Nisan 2020.
Dış bağlantılar
- Teaching Archives of the Materials Digital Library Pathway'de bulunan Taşınım Olayları Arşivi8 Ekim 2017 tarihinde Wayback Machine sitesinde .
- . 25 Aralık 2003 tarihinde kaynağından arşivlendi.
- . 25 Aralık 2003 tarihinde kaynağından arşivlendi.
- . 25 Aralık 2003 tarihinde kaynağından arşivlendi.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Tasinim olayi veya tasinim fenomeni muhendislik fizik ve kimyada gozlemlenen ve uzerine arastirma gerceklestirilen sistemlerin kutle enerji yuk momentum ve acisal momentum degisimiyle ilgilenen calismalardir Surekli ortamlar mekanigi ve termodinamik gibi pek cok farkli alandan yararlanirken ele aldigi konular uzerindeki ortakliklara onemli duzeyde vurgu yapmaktadir Kutle momentum ve isi aktarimi olaylari oldukca benzer bir matematiksel temele sahiptirler Tasinim olayi calismalarinda dogrudan digerlerinden turetilen alanlarin analizinde oldukca kullanisli ve derinlikli matematiksel baglantilar kurmakta bu benzer temellerden faydalanilir Uc alt ana dal olan kutle isi ve momentum aktariminin temel analizi genellikle incelenen buyukluklerin toplaminin sistem ve cevresi tarafindan korunmasi gerektigi ilkesine dayanmaktadir Bu nedenle tasinima sebep olan her olay katkilarinin toplaminin sifira esit olacagi bilgisiyle ayri ayri ele alinirlar Bu ilke ilgili pek cok buyuklugun hesaplanmasinda kullanislidir Ornegin sabit bir hacim boyunca akan bir akiskanin belirlenmesi akiskanlar mekaniginde sikca rastlanan bir tasinim analizidir Tasinim olayi muhendislik disiplinlerinin her yerinde bulunmaktadir Tasinim analizinin en yaygin ornekleri proses kimya ve makine muhendisligi ile biyomuhendislik alanlarinda gorulur ancak akiskanlar mekanigi isi aktarimi ve kutle aktarimi ile uzaktan veya yakindan ilintili tum disiplinlerin mufredatinda temel bir unsurdur Tasinim olayi gunumuzde en az termodinamik mekanik ve elektromanyetizma kadar muhendislik disiplininin bir parcasi olarak kabul edilmektedir Tasinim olaylari evrendeki tum fiziksel degisim etkenlerini kapsamaktadir Dahasi evreni olusturan ve dunya uzerindeki tum yasamin basarisindan sorumlu temel yapi taslarindan biri olarak kabul edilmektedir Ancak burada verilen bilgilerin kapsami tasinim olaylarinin yapay muhendislik sistemleri ile iliskisiyle sinirlidir Genel bakisFizikte tasinim olaylarinin hepsi cogunlukla akiskanlarda gozlemlenen molekullerin surekli ve rastgele hareketlerinden kaynaklanan istatistiksel doganin Tasinim olaylarinin tum unsurlari ve olmak uzere iki temel kavrama dayalidir Tasinim olaylarinin iceriginde bulunan korunum yasalari soz konusu buyuklugun nasil korunacagini tanimlayan halinde formule edilir Temel esitlikler ise soz konusu buyuklugun cesitli etkenlere tasinim yoluyla nasil tepki verdigini tanimlar Buna onemli ornekler arasinda Fourier in Isi Iletim Kanunu ve Navier Stokes denklemleri vardir Fourier kanunu isi akisinin sicaklik gradyanina verdigi tepkiyi tanimlarken Navier Stokes esitlikleri de akiskan akisi ve akiskana uygulanan kuvvetler arasindaki iliskiyi aciklar Bu esitlikler ayni zamanda tasinim olaylari ve termodinamik arasindaki derin baglantiyi yani tasinim olaylarinin neden geri donusumsuz oldugunu aciklayan baglantiyi ortaya koymaktadir Bu fiziksel olaylarin neredeyse tamami minimum enerji prensibine uygun olarak en dusuk enerjili hale gecmeye calisan sistemleri kapsar Sistemler bu hale yaklastikca surucu guclerin sistemde artik yer almadigi ve tasinimda kesintinin olmadigi gercek termodinamik dengeye ulasma egilimi gosterirler Bu turde bir dengenin cesitli yonleri dogrudan isi aktarimina baglidir Kutle ve momentum aktariminin sistemi kimyasal ve mekanik dengeye dogru hareket ettirmesine benzer olarak isi aktarimi da sistemin cevresiyle isil dengeye ulasmaya calismasidir Isi iletimi enerji aktarimi akiskan akisi momentum aktarimi kutle aktarimi radyasyon ve yari iletkenlerde elektrik yuku aktarimi tasinim sureclerine birer ornektir Tasinim olaylarinin genis bir uygulama alani vardir Ornegin kati hal fiziginde elektronlarin deliklerin ve fononlarin hareketi ve etkilesimleri tasinim olaylari altinda incelenir Bir diger ornek de biyomedikal muhendislikte ilgilenilen termoregulasyon perfuzyon ve gibi tasinim olaylaridir Kimya muhendisliginde tasinim olaylari reaktor tasariminda membran analizlerinde molekuler veya difuzif tasinim mekanizmalarinin analizinde ve metalurjide kullanilir Kutle enerji ve momentum aktarimi dis kaynaklar sebebiyle etkilenebilir Bir kokunun yayilma hizi ruzgar hizi sicaklik ve ortamin nemliligi gibi pek cok etkene bagli olarak degisebilir Ornegin cok guclu esen bir ruzgar bir kokuyu hafif bir esintiye gore cok daha uzaklara hizli bir sekilde tasiyabilir Isi iletebilen bir katinin soguma hizi bir isi kaynaginin varligina bagli olarak degisir Bir yagmur damlasina etkiyen yercekimi kuvveti damlayi cevreleyen havanin uyguladigi direnci veya suruklenmeyi etkisizlestirir Olaylar arasindaki ortakliklarTasinim olaylari calismalarindaki onemli bir ilke de olaylar arasindaki benzerliklerdir Difuzyon Asagidaki orneklerde de gosterildigi uzere hepsi de difuzyon yoluyla tasinabilen kutle enerji ve momentum aktarimi denklemleri arasinda onemli benzerlikler vardir Kutle Kokularin havada yayilmasi kutle difuzyonuna bir ornektir Enerji Kati bir malzemede isi iletimi isi difuzyonuna bir ornektir Momentum Bir yagmur damlasinin atmosfer boyunca duserken ugradigi suruklenme bir ornegidir yagmur damlasinin momentumu viskoz gerilmeler sebebiyle onu cevreleyen havaya gecer ve damla yavaslar Akiskan momentumu icin Newton yasasi Fourier in isi kanunu ve molekuler tasinim denklemleri birbirine oldukca benzerdir Uc farkli tasinim olayini birbirleriyle karsilastirmak icin bir tasinim katsayisindan digerine donusum gerceklestirilebilir Difuzyon olayinin karsilastirmasi Tasinan buyukluk Fiziksel olay EsitlikMomentum Viskozite Newton tipi akiskan t n ry x displaystyle tau nu frac partial rho upsilon partial x Enerji Isi iletimi Fourier kanunu q kAdTdx displaystyle q kA frac dT dx Kutle J D C x displaystyle J D frac partial C partial x Esitliklerin tanimlari asagida verilmistir Literaturde turbulent tasinim icin bu uc tasinim olayi arasinda benzerlikler gelistirilerek birinin digerinden tahmin edilebilmesini saglamak icin buyuk caba sarf edilmistir turbulent difuzivitelerin esit oldugunu ve molekuler kutle D AB ile momentum m r difuzivitelerinin turbulent difuzyonla karsilastirildiginda ihmal edilebilir oldugunu varsayar Sistemde sivilar ve surukleme birlikte veya ayri ayri mevcut ise bu benzerlik gecerli degildir Prandtl in ve von Karman inkiler gibi diger benzerlikler de genellikle yetersiz bagintilar vermektedir En basarili ve en cok kullanilan benzerlik Bu benzerlik gazlar ve sivilarin hem laminer hem turbulansli akis rejimlerinde elde edilmis deneysel veriler uzerine kuruludur Deneysel verilere dayanmasina ragmen duz bir plaka uzerindeki laminer akistan elde edilmis kesin cozumun dogrulanmasi icin de kullanilabilir Tum bu veriler kutle aktarimini tahmin etmek icin kullanilir Onsager ters bagintilari Sicaklik madde yogunlugu ve basinc cinsinden tanimlanan akiskan sistemlerinde sicaklik farklarinin sistemin sicak kismindan soguk kisimlarina isi akisina yol actigi bilinmektedir Benzer sekilde basinctaki farkliliklar maddenin yuksek basinctan dusuk basincli bolgelere ters baginti akisina yol acacaktir Sicaklik ve basincin degisebilir oldugu sistemlerde dikkat cekici olan sey sabit basinctayken sicakligin degismesinin madde akisina konveksiyonda oldugu gibi ve sabit sicakliktayken basinc degisiminin isi akisina neden olabilecegi gozlemidir Birim basinc farki basina gerceklesen isi akisi ile birim sicaklik farki basina gerceklesen madde akisi sasirtici bicimde ayni olabilirdi Lars Onsager mikroskobik dinamigin zaman tersinirliginin bir sonucu olarak istatistiksel mekanigi kullanarak bu esitligin gerekli oldugunu gostermistir Onsager tarafindan gelistirilen teori verilen orneklerden cok daha geneldir ve ayni anda ikiden fazla termodinamik kuvveti isleme tabi tutabilir Momentum aktarimiBir akiskanin x yonu boyunca u hizinda laminer akisi Kayma gerilmesi ve hiz gradyani sekilde goruldugu gibidir Akis yonu x olsa da hizin degisim gosterdigi yon y dir Dolayisiyla degisim y yonune bagli u y displaystyle partial u partial y ifadesi ile gosterilir Momentum aktariminda uzerinde calisma yapilan akiskan maddenin surekli bir dagilimi olarak kabul edilir Momentum aktarimi ya da akiskanlar mekanigi akiskanlar statigi hareketsiz akiskanlar ve akiskanlar dinamigi hareket halindeki akiskanlar olmak uzere iki dala ayrilir Bir akiskan kati bir yuzeye paralel x yonunde akarken momentumu x yonunde ve konsantrasyonu yxr olur Molekullerin rastgele difuzyonundan dolayi x yonunde dik olan y yonunde bir molekul degisimi vardir Bu nedenle x yonune akistaki momentum y yonu boyunca hizli hareket eden katmandan yavas hareket eden katmana dogru aktarilir Yani momentum x yonu boyunca sabitken y yonunde yani akiskanin katmanlari boyunca degisir Buna dayali olarak momentum aktarim denklemi olan Newton un Viskozite Kanunu asagidaki gibi yazilir tyx n ryx y displaystyle tau yx nu frac partial rho upsilon x partial y Burada txy x yonunde akan akiskanin y yonu boyunca olusan kayma gerilmesidir Momentum akisi olarak da adlandirilir n kinematik viskozitedir ve m r olarak da ifade edilir y tasinim veya difuzyonun gerceklestigi mesafedir r yogunluk ve m da dinamik viskozitedir Newton Yasasi momentum akisi ile hiz gradyani arasindaki en basit iliskidir Kutle aktarimiBir siseye hapsolmus gaz yesil renkli sisenin kapagi acildiginda derisimin az oldugu ortama hareket edecektir Bir sistemde derisim bir noktadan baska bir noktaya degisiyorsa kutlenin sistemdeki derisim farkini en aza indirecek sekilde tasinimina dogal bir egilim bulunmaktadir Bir sistemdeki kutle aktarimi Birinci Fick Kanunu ile belirlenir Yuksek derisimden dusuk derisime gerceklesen difuzyonun akisi ortamdaki maddenin derisim gradyani ve difuzivitesi ile orantilidir Kutle aktarimi farkli itici gucler yoluyla gerceklesebilir Bunlardan bazilari Kutle bir basinc gradyaninin etkisiyle aktarilabilir basinc difuzyonu Bazi dis kuvvetlerin etkisiyle zorlanmis difuzyon olusabilir Sicaklik gradyanlarindan oturu difuzyon gerceklesebilir termal difuzyon farklardan dolayi difuzyon gerceklesebilir A ve B den olusan bir karisimda A nin difuzyonu asagida verilen Fick in Difuzyon Kanunu ile belirlenir JAx DAB Ca x displaystyle J Ax D AB frac partial Ca partial x Burada DAB difuzyon katsayisi x difuzyon yonu JAx A maddesinin x yonu boyunca molar difuzyon hizi Ca ise A nin derisimidir Enerji aktarimiBirbirine temas eden iki ortamda isi sicakligi yuksek Th olan ortamdan soguk Tc olan ortama dogal olarak iletilir Buna isi iletimi adi verilir Buna ek olarak isi konveksiyon isi tasinimi ve radyasyon isinim yollari ile de yayilabilir Muhendislikteki tum sureclerde enerji aktarimi bulunmaktadir Buna ornek olarak proses akimlarinin isitilmasi ve sogutulmasi hal degisimleri distilasyon ve benzeri islemler verilebilir Temel ilke bir statik sistem icin asagidaki gibi ifade edilmis olan termodinamigin ilk kanunudur q kdTdx displaystyle q k frac dT dx Bir sistem boyunca net enerji akisi q isi iletim katsayisi k ve sicakligin mekana gore degisim hizinin dT dx carpimina esittir Isi iletim katsayisi ve enerji akisinin birimlerine bagli olarak bu denkleme kesit yuzey alani da A eklenebilir Turbulansli akis karmasik geometriler veya islem yapilmasi zor sinir kosullari iceren diger sistemler icin baska bir denklemin kullanimi daha kolay olacaktir Bu denklem isi tasinim konveksiyon denklemidir Q h A DT displaystyle Q h cdot A cdot Delta T Burada A yuzey alani DT displaystyle Delta T isi aktarimina sebep olan sicaklik farki Q birim zamanda aktarilan isi miktari ve h de isi iletim katsayisidir Isi aktariminda iki tur tasinim konveksiyon gerceklesebilir veya zorlanmis konveksiyon hem laminer hem de turbulansli akista gerceklesebilir Dairesel borularda laminer akisin gerceklestigi durumlarda Nusselt sayisi Reynolds sayisi ve Prandtl sayisi gibi cesitli boyutsuz sayilar kullanilmaktadir Yaygin olarak kullanilan denklem asagidaki gibidir Nua haDk displaystyle Nu a frac h a D k veya konveksiyon Grashof ve Prandtl sayilarinin bir fonksiyonudur Dogal konveksiyon ile isi transferinin karmasikligi deneysel verilerden turetilen ampirik iliskilerin kullanilmasini gerekli kilmaktadir Isi aktarimi nukleer reaktorler kimyasal reaktorler ve isi degistiriciler gibi endustriyel ekipmanlarda analiz edilmektedir UygulamalarKirlilik Tasinim sureclerinin arastirilmasi kirleticilerin cevreye salinimi ve yayiliminin anlasilabilmesi icin onemlidir Dogru bir modelleme kirlilik azaltma stratejilerinin belirlenmesine ozellikle yardimci olabilir Kentsel akistan kaynakli su yuzeyi kirliliginin kontrolu ve ABD deki araclarin fren balatalarinin bakir icerigini azaltmayi amaclayan politikalar gibi nice calisma tasinim olaylari uygulamalarina birer ornek olarak verilebilir Ayrica bakinizSureklilik denklemi Aksiyon potansiyeli Biyolojik isi transferiKaynakca Truskey George Yuan F Katz D 2009 Transport Phenomena in Biological Systems Second ed Ingilizce s 888 ISBN 978 0131569881 Transport phenomena fundamentals Chemical Industries Series CRC Press Nisan 2001 ss 1 2 3 ISBN 978 0 8247 0500 8 7 Eylul 2014 tarihinde kaynagindan Erisim tarihi 20 Haziran 2020 Plawsky Joel Transport Phenomena Fundamentals Marcel Dekker Inc 2009 Alonso amp Finn Physics Addison Wesley 1992 Chapter 18 Deen William M Analysis of Transport Phenomena Oxford University Press 1998 J M Ziman Electrons and Phonons The Theory of Transport Phenomena in Solids Oxford Classic Texts in the Physical Sciences Griswold S S 1962 Air Pollution Control Field Operations Manual A Guide for Inspection and Enforcement Ingilizce U S Department of Health Education and Welfare ss 203 204 22 Haziran 2020 tarihinde kaynagindan Erisim tarihi 20 Haziran 2020 Welty James R Wicks Charles E Wilson Robert Elliott 1976 Fundamentals of momentum heat and mass transfer 2 bas Wiley 3 Agustos 2020 tarihinde kaynagindan Erisim tarihi 20 Haziran 2020 Thomas William J Introduction to Transport Phenomena Prentice Hall Upper Saddle River NJ 2000 Transport Phenomena 1 bas Nirali Prakashan 2006 s 15 3 ISBN 81 85790 86 8 19 Agustos 2020 tarihinde kaynagindan Erisim tarihi 20 Haziran 2020 Chapter 15 p 15 3 19 Agustos 2020 tarihinde Wayback Machine sitesinde Onsager 15 Subat 1931 Reciprocal Relations in Irreversible Processes I Physical Review American Physical Society APS 37 4 405 426 a b Griskey Richard G Transport Phenomena and Unit Operations Wiley amp Sons Hoboken 2006 228 248 Muller 20 Mart 2020 The pollution conveyed by urban runoff A review of sources Science of the Total Environment Ingilizce 709 136125 21 Haziran 2020 tarihinde kaynagindan Erisim tarihi 20 Haziran 2020 Copper Free Brake Initiative US EPA Ingilizce 10 Kasim 2015 29 Aralik 2015 tarihinde kaynagindan Erisim tarihi 1 Nisan 2020 Dis baglantilarTeaching Archives of the Materials Digital Library Pathway de bulunan Tasinim Olaylari Arsivi8 Ekim 2017 tarihinde Wayback Machine sitesinde 25 Aralik 2003 tarihinde kaynagindan arsivlendi 25 Aralik 2003 tarihinde kaynagindan arsivlendi 25 Aralik 2003 tarihinde kaynagindan arsivlendi