Termodinamik; ısı, iş, sıcaklık ve enerji arasındaki ilişki ile ilgilenen bilim dalıdır. Basit bir ifadeyle termodinamik, enerjinin bir yerden başka bir yere ve bir biçimden başka bir biçime transferi ile ilgilenir. Bu süreçteki anahtar kavram, ısının, belirli bir mekanik işe denk gelen bir enerji biçimi olmasıdır.

Termodinamik kavramı Yunanca Yunanca: thermos (ısı) ve Yunanca: dynamic (enerji) kelimelerinden türetilmiştir. Bazı Türkçe kaynaklarda ısıl devingi olarak da geçer. Enerji, ısı, iş, entropi ve ekserji gibi fiziksel kavramlarla ilgilenir. Termodinamik yasalarının istatistiksel mekanikten türetilebileceği gösterilmiştir.[]

Termodinamik her ne kadar sistemlerin madde ve/veya enerji alış-verişiyle ilgilense de, bu işlemlerin hızıyla ilgilenmez. Bundan dolayı aslında termodinamik denilirken, denge termodinamiği kastedilir. Bu yüzden termodinamiğin ana kavramlarından biri "quasi-statik" (yarı-durağan) adı verilen, idealize edilmiş "sonsuz yavaşlıkta" olaylardır. Zamana bağlı termodinamik olaylarla, denge halinde olmayan termodinamik ilgilenir.
Termodinamik yasaları çok genel bir geçerliliğe sahiptirler ve karşılıklı etkileşimlerin ayrıntılarına veya incelenen sistemin özelliklerine bağlı olarak değişmezler. Yani bir sistemin sadece madde veya enerji giriş-çıkışı bilinse dahi bu sisteme uygulanabilirler.
Termodinamik değişkenler
Bu değişkenler genellikle sistemin ya kendisini ya da çevre koşullarını tarif etmek için kullanılır. En çok kullanılanlar ve simgeleri şunlardır:
- Mekanik değişkenler:
- İstatistiksel değişkenler:
Mekanik değişkenler, temel klasik veya parçacık fiziği tanımlarıyla tarif edilebilirken, istatistiksel değişkenler sadece istatistiksel mekanik tanımlarıyla anlaşılabilir.
Termodinamiğin çoğu uygulamasında, bir ya da daha çok değişken sabit tutulurken diğer değişkenlerin bunlara göre nasıl değiştiği incelenir ve bu da sistemin matematiksel olarak (n sabit tutulmayan değişkenlerin sayısı olmak üzere) n boyutlu bir uzay olarak tarif edilebileceği anlamına gelir. İstatistiksel mekaniği fizik yasalarıyla birleştirerek, bu değişkenleri birbirleri cinsinden ifade edecek "durum denklemleri" yazılabilir. Bunların en basit ve en önemli olanlarından biri ise ideal gaz yasasıdır.
Bu denklemde R 'dir. Ayrıca istatistiksel mekanik terimleriyle bu denklem şöyle yazılır:
Bu denklemde de k Boltzmann sabiti'dir.
Termodinamik potansiyeller
Termodinamik değişkenler vasıtasıyla dört tane termodinamik tanımlanabilir:
| Sistemin iç enerjisi |  |  |
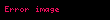 | 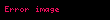 | |
| Gibbs serbest enerjisi | 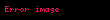 | 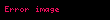 |
| Entalpi | 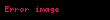 | 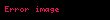 |
Entalpi, özel bir fonksiyondur. Basınç sabit olduğu zaman bize ısıyı verir. Bu dört potansiyelin diferansiyel denklemlerini ve zincirleme türev kuralını kullanarak bu dört potansiyel, değişkenler ve birbirleri cinsinden yazılabilir:
Termodinamik kanunları
Sıfırıncı kanun
İki sistem birbirleri ile etkileşim halinde oldukları halde, durumları değişmeden kalıyorsa bu iki sistem birbirleri ile dengededir denilir. Eğer iki sistem etkileşime açık oldukları halde, aralarında mekanik etkileşimle olan enerji transferi (iş) dışında net enerji transferi (ısı geçişi) yoksa, bu iki sistem birbirleri ile ısıl dengededirler. Sıfırıncı yasa şöyle der:
Eğer A ve B sistemleri birbirleri ile ısıl dengede ise, A sistemi ile ısıl dengede olan bir C sistemi, B sistemi ile de ısıl denge durumundadır.
Bu denge durumu, sıcaklık olarak tanımlanır. Yani her sıcaklık derecesi, farklı bir denge durumunu temsil eder. Bu durum:
TA=TB=TC şeklinde formülize edilir.
1931 yılında Ralph H. Fowler tarafından tanımlanan bu yasa, temel bir fizik ilkesi olarak karşımıza çıktığından, doğal olarak 1. ve 2. yasalardan önce gelmek zorunluluğu doğmuş ve sıfırıncı yasa adını almıştır.
Bu yasanın uygulanışına örnek olarak termometreler verilebilir. Termometre "üçüncü sistem" olarak kullanılır ve bir sıcaklık ölçeği oluşturulmasına imkân verir.
Birinci kanun
Termodinamiğin birinci yasası "enerjinin korunumu" olarak da bilinir. Bu yasaya göre:
Bir sistemin iç enerjisindeki değişim miktarı, o sisteme ilave edilen ısı miktarı ile sistemin çevresine uyguladığı iş arasındaki farka eşittir.
Bu durum şöyle gösterilir:
- U2 – U1 = Q – W
Enerji yoktan var edilemez ve yok edilemez sadece bir şekilden diğerine dönüşür. Bir sistemin herhangi bir çevrimi için çevrim sırasında ısı alışverişi ile iş alışverişi aynı birim sisteminde birbirlerine eşit farklı birim sistemlerinde ise birbirlerine orantılı olmak zorundadır. Bu ifadelerin yapılan deneylerle doğruluğu gözlenmiştir fakat ispat edilememektedir. Bütün bu ifadeler matematiksel olarak çok daha kolay ifade edilebilir.
Aşağıdaki formüllerde
- Q = çevrim boyunca net ısı alışverişini
- W = çevrim boyunca net iş alışverişini
göstermektedir. Çevrim de şu şekilde gösterilmiştir:

Şimdi bu şekilde sistemin herhangi iki hali görünüyor yani 1 ve 2 nolu noktalar. Hal değişimleri ise A, B, C çizgileriyle sağlansın. Ok yönleri de hal değişimlerinin olacağı yönler. Şimdi hal değişimleri 1A2 ve 1B2 ise 2C1 ilk hale dönülen durumdur. Şimdi çevrimleri kurgulayalım elimizde 1A2C1 ve 1B2C1 çevrimleri var:
- 1A∫2.δ.Q + 2C∫1.δ.Q = 1A∫2.δ.W + 2C∫1.δ.W (1A2C1 çevrimi) (a denklemi)
- 1B∫2.δ.Q + 2C∫1.δ.Q = 1B∫2.δ.W + 2C∫1.δ.W (1B2C1 çevrimi) (b denklemi)
1A2C1 ve 1B2C1 çevrimleri birbirlerine eşittir. Termodinamiğin 1. kanunu uygulandığında a ve b denklemleri ortaya çıkar b denklemi a denkleminden çıkarırsak c denklemi bulunur.
- 1A∫2 (δQ - δW) = 1B∫2(δQ - δW) (c denklemi)
1A2 ve 1B2 aynı haller arasında herhangi iki hal değişimi olduğundan δQ – δW ifadesinin 1-2 noktası arasındaki bütün hal değişimleri için bağımsız olduğu söylenebilir. Bunların farkı nokta fonksiyonudur ve tam diferansiyeldir. Bu sisteme has bir özellik olup sistemin enerjisidir ve E ile gösterilir (E=δQ-δW) sonsuz küçük hal değişimi için bu formülün integrali alınırsa;
- Q1-2 : Sistemin hal değişimindeki ısı alışverişi
- W1-2 : Sistemin hal değişimindeki iş alışverişi
- E1 : Sistemin ilk haldeki enerjisi ve
- E2 : Sistemin son haldeki enerjisi
olmak üzere;
- Q1-2 – W1-2 = E2 – E1
formülü çıkar. Termodinamikte enerji, maddenin yapısına bağlı iç enerji ve koordinat eksenlerine bağlı olan kinetik enerji (EK) ve potansiyel enerji (EP) olarak ayrılabilir;
- E = U + EK + EP
Sistemin herhangi bir hal değişimindeki enerjisi de;
- Q1-2 – W1-2 = E2 – E1 = (U2 – U1) + (1/2) m (V22 – V12) + m g (h2 – h1)
- U: iç enerji
- m: kütle
- V: hız
- g: yerçekimi ivmesi
- h: yükseklik
İkinci kanun
Termodinamiğin ikinci yasası şu şekildedir:
Isı, soğuk bir bölgeden sıcak bir bölgeye kendiliğinden akamaz; başka bir deyişle, belirli bir sıcaklık derecesindeki ısı, tamamen işe dönüşemez.
Bunun bir sonucu olarak, kapalı bir sistemin entropisi zaman içerisinde en yüksek değerine ulaşır. Yani, tüm kapalı sistemler bir denge hâline ulaşmaya meyleder ve bu denge hâlinde entropi en yüksek düzeyde iken iş yapabilecek enerji miktarı sıfırdır. Bu ileri-geri asimetrik süreç fizikte "" denen kavramın yaratılmasına neden olmuştur.
Bir ısı kaynağından ısı çekip buna eşit miktarda iş yapan ve başka hiçbir sonucu olmayan bir döngü elde etmek imkânsızdır. (Kelvin-Planck Bildirisi)
Verim asla 1'den büyük olamaz. Dolayısıyla tek kaynaktan ısı alarak çalışan bir makine yapmak olası değildir.[]
Soğuk bir cisimden sıcak bir cisme ısı akışı dışında bir etkisi olmayan bir işlem elde etmek imkânsızdır. (Clausius Bildirisi)
Termal olarak izole edilmiş büyük bir sistemin entropisi hiçbir zaman azalmaz (bkz: Maxwell'in Cini). Ancak mikroskopik bir sistem, yasanın dediğinin tersine entropi dalgalanmaları yaşayabilir (bkz: ). Aslında, dalgalanma teoreminin zamana göre tersinebilir dinamik ve nedensellik ilkesinden çıkan matematiksel kanıtı ikinci yasanın bir kanıtını oluşturur. Mantıksal bakımdan ikinci yasa bu şekilde aslında fiziğin bir yasasından ziyade göreli olarak büyük sistemler ve uzun zamanlar için geçerli bir teoremi haline gelir. Ludwig Boltzmann tarafından tanımlanmıştır. Sisteme dışarıdan enerji verilmediği sürece düzenin düzensizliğe düzensizliğin de kaosa dönüşeceğini anlatır. Kırık bir bardağın durup dururken veya kırarken harcanan enerjiden daha azı kullanılarak eski haline döndürülemeyeceği örneği verilir klasik olarak. Yine aynı şekilde devrilen bir kitabı düzeltmek için devirirken harcanan enerjiden fazlasını kullanmak gerekir, potansiyel enerjinin bir kısmı ısıya dönüşmüştür ve geri getirilemez. Aynı zamanda Evren'deki düzensizlik eğilimini de anlatır. Düzensizlik eğilimini anlatırken entropi kelimesini kullanır. Yunanca, en = İngilizcedeki 'in' gibidir, önüne geldiği kelimeye -de, -da eki verir ve tropos = yol kelimesinin çoğulu olan 'tropoi' (tropi diye telaffuz edilir) kelimesinden. Yani; "yolda").
- Düzensizlik ya değişmez ya da artar. Örnek olarak difüzyon verilebilir. Ayrı duran maddeler bir arada olandan daha düzenlidir ve kendiliğinden karışmış sıcak ve soğuk sudan oluşmuş ılık suyun, bir daha sıcak ve soğuk diye ayrılması imkânsızdır.
- Eskime, yaşlanma, yıllanma gibi eylemlerin nedenidir.
- En düzensiz enerji ısıdır ve bir gün gelecek bütün enerji ısı olacaktır ve bu da Evren'in sonu demektir.
- İleri sürülecek teoriler termodinamiğin 2. kanunuyla çelişmemelidir.
- Entropi iş yapma yeteneği olmayan enerji olarak da tanımlanır. İki cam balona farklı sıcaklıklarda gaz, cam balonlar arasına da bir pervane konacak olursa ilk başta pervanenin döndüğünü görülecektir. Fakat sonra entropi arttığı için pervanenin dönmesi duracaktır.
- Spor yapmak için bir parkta 100 metrelik bir koşu yapıldığını, 100 metrenin sonunda yorulup koşamayacak hale gelindiğini ve bir yere oturulduğu düşünülecek olursa koşarken harcanmış olan ve bir daha kazanılamayacak olan enerjiye entropi denir.
- Sistemin düzensizliği arttıkça artan herhangi bir fonksiyon rahatça entropi fonsiyonu olabilir. Örneğin bir bardak suyumuz olduğunu ve bunun içine bir damla mürekkep damlatıp gözlediğimizi düşünelim ve içeride neler olduğunu hayal etmeye çalışalım. Mürekkep molekülleri başlangıçta kısa bir süre bir arada bekleştikten sonra su içine dağılmaya başlayacaklardır. Çünkü kendilerine çarpan su molekülleri tarafından değişik yönlere itileceklerdir (su ve mürekkep maddelerinin kimyasal bağlarının birbirlerini itmeye elverişli olmalarından dolayı). Şimdi de olağanüstü bir bilgisayarın, sistemin bütün mümkün durumlarını sayabildiğini düşünelim. Sistemin bir durumu denildiğinde anlamamız gereken şey bir molekülün belirli bir koordinata ve belirli bir hıza; bir başka molekülun bir başka belirli koordinata ve hıza sahip olduğu konfigürasyondur. Bardaktaki mürekkep örneğinde bu tür durumların sayısının çok fazla olduğu açıktır. Zîrâ bunların çok büyük bir kısmı mürekkebin moleküllerinin bardak içinde oraya buraya rastgele dağıldığı, düzensiz, yani yüksek entropili durumlara karşılık gelirler. Bizim algıladığımız düzeyde bunların hepsi homojen durumlardır. Çünkü karışıma baktığımızda o molekülün burada, bir başkasının şurada olmasına aldırmadan, mürekkebin homojen olarak dağıldığını söyleyebiliriz. Yani olağanüstü sayıda farklı mikroskopik durum tek bir makroskobik duruma, yani homojen duruma karşılık gelir.
- Aslında sistemler bozulmamakta, enerji değişimi bazında en kararlı hali almaya çalışmaktadırlar. Hayatın anlamı da budur, yaşam entropi yollarından biridir, şekerin çaya çok daha çabuk karışmasını sağlayan kaşık işlevindedir.
- Kapalı bir sistemde entropi her zaman artar. Kapalı sistem kısmı çok önemlidir. Sisteme enerji vermek suretiyle entropisi azaltılabilir. Dünya, kapalı bir sistem değildir. Güneş'ten sürekli olarak enerji akmaktadır ve düzeni bu sağlar.
- "Parçacık sayısı sonsuza giderken olması en muhtemel olan şey olur": Havaya bir miktar bozuk para atılsa hepsinin tura gelme ihtimali yalnızca birdir. Biri dışında hepsinin tura gelme ihtimali daha çoktur. Yarısının yazı, yarısının tura gelme ihtimali daha da çoktur. İşte bu sonuncusu maksimum entropiye sahip olan sistemdir. Sonuç olarak entropinin artması, sistemin muhtemel olmayan durumdan daha çok muhtemel olan duruma doğru gitmesi demektir. İçinde bulunulan odadaki moleküllerin hepsinin odanın sağ köşesindeki bir noktaya toplanması mümkünse de bu koşulu sağlayan yalnızca bir konfigürasyon vardır. Oysa atomların odanın her yerine eşit dağıldığı daha çok konfigürasyon vardır.
Üçüncü kanun
Üçüncü yasa şu şekildedir:
Sıcaklık mutlak sıfıra yaklaştıkça, en durağan hâlindeki bir elementin kusursuz bir kristalinin entropisi de sıfıra yaklaşır.
Bu durum, istatistiksel bir bakış açısıyla, bir sistemdeki düzenin veya rastgeleliğin seviyesini belirleyen mutlak bir entropi ölçeği oluşturulmasına imkân verir.
Bu yasa neden bir maddeyi mutlak sıfıra kadar soğutmanın imkânsız olduğunu izah eder;[] zîrâ sıcaklık mutlak sıfıra yaklaştıkça hareketlilik miktarı da sıfıra yaklaşır.
Sıcaklık mutlak sıfıra yaklaştıkça, bir sistemin entropisi bir sabite yaklaşır. Bu sayının sıfır değil de bir sabit olmasının sebebi, bütün hareketler durmasına ve buna bağlı olan belirsizliklerin yok olmasına rağmen kristal olmayan maddelerin moleküler dizilimlerinin farklı olmasından kaynaklanan bir belirsizliğin hâlâ mevcut olmasıdır. Ayrıca üçüncü yasa sayesinde maddelerin mutlak sıfırdaki entropileri referans alınmak üzere kimyasal tepkimelerin incelenmesinde çok yararlı olan mutlak entropi tanımlanabilir.
Alıntılar
"Bu evde termodinamik kurallarına uyarız!" (Lisa enerjisi zamanla artan bir devridaim makinası yaptıktan sonra) – Homer Simpson
"Termodinamik komik bir konudur. İlk defa öğrendiğinizde, ne olduğunu anlamazsınız bile. İkinci defa üzerinden geçtiğinizde, bir-iki nokta hariç anladığınızı düşünürsünüz. Üçüncü defa baktığınızda ise, anlamadığınızı bilirsiniz, ama o zamana kadar konuya alıştığınız için bu sizi o kadar rahatsız etmez." – Arnold Sommerfeld
"Dökülen sütün arkasından ağlamayın, Evren'in bütün kuvvetleri sütü dökmeyi aklına koymuştu bir kez." -
| Wikimedia Commons'ta Termodinamik ile ilgili ortam dosyaları bulunmaktadır. |
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Termodinamik isi is sicaklik ve enerji arasindaki iliski ile ilgilenen bilim dalidir Basit bir ifadeyle termodinamik enerjinin bir yerden baska bir yere ve bir bicimden baska bir bicime transferi ile ilgilenir Bu surecteki anahtar kavram isinin belirli bir mekanik ise denk gelen bir enerji bicimi olmasidir Basitlestirilmis uc genlesme motorlu animasyon Yuksek basincli buhar kirmizi kazandan girer ve motordan gecerek kondansatore dusuk basincli buhar mavi olarak varir Termodinamik kavrami Yunanca Yunanca thermos isi ve Yunanca dynamic enerji kelimelerinden turetilmistir Bazi Turkce kaynaklarda isil devingi olarak da gecer Enerji isi is entropi ve ekserji gibi fiziksel kavramlarla ilgilenir Termodinamik yasalarinin istatistiksel mekanikten turetilebilecegi gosterilmistir kaynak belirtilmeli Sadi Carnot 1796 1832 termodinamik biliminin kurucusu olarak kabul edilir Termodinamik her ne kadar sistemlerin madde ve veya enerji alis verisiyle ilgilense de bu islemlerin hiziyla ilgilenmez Bundan dolayi aslinda termodinamik denilirken denge termodinamigi kastedilir Bu yuzden termodinamigin ana kavramlarindan biri quasi statik yari duragan adi verilen idealize edilmis sonsuz yavaslikta olaylardir Zamana bagli termodinamik olaylarla denge halinde olmayan termodinamik ilgilenir Termodinamik yasalari cok genel bir gecerlilige sahiptirler ve karsilikli etkilesimlerin ayrintilarina veya incelenen sistemin ozelliklerine bagli olarak degismezler Yani bir sistemin sadece madde veya enerji giris cikisi bilinse dahi bu sisteme uygulanabilirler Termodinamik degiskenlerBu degiskenler genellikle sistemin ya kendisini ya da cevre kosullarini tarif etmek icin kullanilir En cok kullanilanlar ve simgeleri sunlardir Mekanik degiskenler Basinc P Hacim V Istatistiksel degiskenler Sicaklik T Entropi duzensizlik S Mekanik degiskenler temel klasik veya parcacik fizigi tanimlariyla tarif edilebilirken istatistiksel degiskenler sadece istatistiksel mekanik tanimlariyla anlasilabilir Termodinamigin cogu uygulamasinda bir ya da daha cok degisken sabit tutulurken diger degiskenlerin bunlara gore nasil degistigi incelenir ve bu da sistemin matematiksel olarak n sabit tutulmayan degiskenlerin sayisi olmak uzere n boyutlu bir uzay olarak tarif edilebilecegi anlamina gelir Istatistiksel mekanigi fizik yasalariyla birlestirerek bu degiskenleri birbirleri cinsinden ifade edecek durum denklemleri yazilabilir Bunlarin en basit ve en onemli olanlarindan biri ise ideal gaz yasasidir P V n R T displaystyle P cdot V n cdot R cdot T Bu denklemde R dir Ayrica istatistiksel mekanik terimleriyle bu denklem soyle yazilir P V N k T displaystyle P cdot V N cdot k cdot T Bu denklemde de k Boltzmann sabiti dir Termodinamik potansiyellerTermodinamik degiskenler vasitasiyla dort tane termodinamik tanimlanabilir Sistemin ic enerjisi E displaystyle E dE T dS P dV displaystyle dE T cdot dS P cdot dV A displaystyle A dA S dT P dV displaystyle dA S cdot dT P cdot dV Gibbs serbest enerjisi G displaystyle G dG S dT V dP displaystyle dG S cdot dT V cdot dP Entalpi H displaystyle H dH T dS V dP displaystyle dH T cdot dS V cdot dP Entalpi ozel bir fonksiyondur Basinc sabit oldugu zaman bize isiyi verir Bu dort potansiyelin diferansiyel denklemlerini ve zincirleme turev kuralini kullanarak bu dort potansiyel degiskenler ve birbirleri cinsinden yazilabilir E H P V A T S displaystyle E H P cdot V A T cdot S A E T S G P V displaystyle A E T cdot S G P cdot V G A P V H T S displaystyle G A P cdot V H T cdot S H G T S E P V displaystyle H G T cdot S E P cdot V Termodinamik kanunlariSifirinci kanun Iki sistem birbirleri ile etkilesim halinde olduklari halde durumlari degismeden kaliyorsa bu iki sistem birbirleri ile dengededir denilir Eger iki sistem etkilesime acik olduklari halde aralarinda mekanik etkilesimle olan enerji transferi is disinda net enerji transferi isi gecisi yoksa bu iki sistem birbirleri ile isil dengededirler Sifirinci yasa soyle der Eger A ve B sistemleri birbirleri ile isil dengede ise A sistemi ile isil dengede olan bir C sistemi B sistemi ile de isil denge durumundadir Bu denge durumu sicaklik olarak tanimlanir Yani her sicaklik derecesi farkli bir denge durumunu temsil eder Bu durum TA TB TC seklinde formulize edilir 1931 yilinda Ralph H Fowler tarafindan tanimlanan bu yasa temel bir fizik ilkesi olarak karsimiza ciktigindan dogal olarak 1 ve 2 yasalardan once gelmek zorunlulugu dogmus ve sifirinci yasa adini almistir Bu yasanin uygulanisina ornek olarak termometreler verilebilir Termometre ucuncu sistem olarak kullanilir ve bir sicaklik olcegi olusturulmasina imkan verir Birinci kanun Termodinamigin birinci yasasi enerjinin korunumu olarak da bilinir Bu yasaya gore Bir sistemin ic enerjisindeki degisim miktari o sisteme ilave edilen isi miktari ile sistemin cevresine uyguladigi is arasindaki farka esittir Bu durum soyle gosterilir U2 U1 Q W Enerji yoktan var edilemez ve yok edilemez sadece bir sekilden digerine donusur Bir sistemin herhangi bir cevrimi icin cevrim sirasinda isi alisverisi ile is alisverisi ayni birim sisteminde birbirlerine esit farkli birim sistemlerinde ise birbirlerine orantili olmak zorundadir Bu ifadelerin yapilan deneylerle dogrulugu gozlenmistir fakat ispat edilememektedir Butun bu ifadeler matematiksel olarak cok daha kolay ifade edilebilir Asagidaki formullerde Q cevrim boyunca net isi alisverisini W cevrim boyunca net is alisverisini gostermektedir Cevrim de su sekilde gosterilmistir Simdi bu sekilde sistemin herhangi iki hali gorunuyor yani 1 ve 2 nolu noktalar Hal degisimleri ise A B C cizgileriyle saglansin Ok yonleri de hal degisimlerinin olacagi yonler Simdi hal degisimleri 1A2 ve 1B2 ise 2C1 ilk hale donulen durumdur Simdi cevrimleri kurgulayalim elimizde 1A2C1 ve 1B2C1 cevrimleri var 1A 2 d Q 2C 1 d Q 1A 2 d W 2C 1 d W 1A2C1 cevrimi a denklemi 1B 2 d Q 2C 1 d Q 1B 2 d W 2C 1 d W 1B2C1 cevrimi b denklemi 1A2C1 ve 1B2C1 cevrimleri birbirlerine esittir Termodinamigin 1 kanunu uygulandiginda a ve b denklemleri ortaya cikar b denklemi a denkleminden cikarirsak c denklemi bulunur 1A 2 dQ dW 1B 2 dQ dW c denklemi 1A2 ve 1B2 ayni haller arasinda herhangi iki hal degisimi oldugundan dQ dW ifadesinin 1 2 noktasi arasindaki butun hal degisimleri icin bagimsiz oldugu soylenebilir Bunlarin farki nokta fonksiyonudur ve tam diferansiyeldir Bu sisteme has bir ozellik olup sistemin enerjisidir ve E ile gosterilir E dQ dW sonsuz kucuk hal degisimi icin bu formulun integrali alinirsa Q1 2 Sistemin hal degisimindeki isi alisverisi W1 2 Sistemin hal degisimindeki is alisverisi E1 Sistemin ilk haldeki enerjisi ve E2 Sistemin son haldeki enerjisi olmak uzere Q1 2 W1 2 E2 E1 formulu cikar Termodinamikte enerji maddenin yapisina bagli ic enerji ve koordinat eksenlerine bagli olan kinetik enerji EK ve potansiyel enerji EP olarak ayrilabilir E U EK EP Sistemin herhangi bir hal degisimindeki enerjisi de Q1 2 W1 2 E2 E1 U2 U1 1 2 m V22 V12 m g h2 h1 U ic enerji m kutle V hiz g yercekimi ivmesi h yukseklikIkinci kanun Termodinamigin ikinci yasasi su sekildedir Isi soguk bir bolgeden sicak bir bolgeye kendiliginden akamaz baska bir deyisle belirli bir sicaklik derecesindeki isi tamamen ise donusemez Bunun bir sonucu olarak kapali bir sistemin entropisi zaman icerisinde en yuksek degerine ulasir Yani tum kapali sistemler bir denge haline ulasmaya meyleder ve bu denge halinde entropi en yuksek duzeyde iken is yapabilecek enerji miktari sifirdir Bu ileri geri asimetrik surec fizikte denen kavramin yaratilmasina neden olmustur Bir isi kaynagindan isi cekip buna esit miktarda is yapan ve baska hicbir sonucu olmayan bir dongu elde etmek imkansizdir Kelvin Planck Bildirisi Verim asla 1 den buyuk olamaz Dolayisiyla tek kaynaktan isi alarak calisan bir makine yapmak olasi degildir kaynak belirtilmeli Soguk bir cisimden sicak bir cisme isi akisi disinda bir etkisi olmayan bir islem elde etmek imkansizdir Clausius Bildirisi Termal olarak izole edilmis buyuk bir sistemin entropisi hicbir zaman azalmaz bkz Maxwell in Cini Ancak mikroskopik bir sistem yasanin dediginin tersine entropi dalgalanmalari yasayabilir bkz Aslinda dalgalanma teoreminin zamana gore tersinebilir dinamik ve nedensellik ilkesinden cikan matematiksel kaniti ikinci yasanin bir kanitini olusturur Mantiksal bakimdan ikinci yasa bu sekilde aslinda fizigin bir yasasindan ziyade goreli olarak buyuk sistemler ve uzun zamanlar icin gecerli bir teoremi haline gelir Ludwig Boltzmann tarafindan tanimlanmistir Sisteme disaridan enerji verilmedigi surece duzenin duzensizlige duzensizligin de kaosa donusecegini anlatir Kirik bir bardagin durup dururken veya kirarken harcanan enerjiden daha azi kullanilarak eski haline dondurulemeyecegi ornegi verilir klasik olarak Yine ayni sekilde devrilen bir kitabi duzeltmek icin devirirken harcanan enerjiden fazlasini kullanmak gerekir potansiyel enerjinin bir kismi isiya donusmustur ve geri getirilemez Ayni zamanda Evren deki duzensizlik egilimini de anlatir Duzensizlik egilimini anlatirken entropi kelimesini kullanir Yunanca en Ingilizcedeki in gibidir onune geldigi kelimeye de da eki verir ve tropos yol kelimesinin cogulu olan tropoi tropi diye telaffuz edilir kelimesinden Yani yolda Duzensizlik ya degismez ya da artar Ornek olarak difuzyon verilebilir Ayri duran maddeler bir arada olandan daha duzenlidir ve kendiliginden karismis sicak ve soguk sudan olusmus ilik suyun bir daha sicak ve soguk diye ayrilmasi imkansizdir Eskime yaslanma yillanma gibi eylemlerin nedenidir En duzensiz enerji isidir ve bir gun gelecek butun enerji isi olacaktir ve bu da Evren in sonu demektir Ileri surulecek teoriler termodinamigin 2 kanunuyla celismemelidir Entropi is yapma yetenegi olmayan enerji olarak da tanimlanir Iki cam balona farkli sicakliklarda gaz cam balonlar arasina da bir pervane konacak olursa ilk basta pervanenin dondugunu gorulecektir Fakat sonra entropi arttigi icin pervanenin donmesi duracaktir Spor yapmak icin bir parkta 100 metrelik bir kosu yapildigini 100 metrenin sonunda yorulup kosamayacak hale gelindigini ve bir yere oturuldugu dusunulecek olursa kosarken harcanmis olan ve bir daha kazanilamayacak olan enerjiye entropi denir Sistemin duzensizligi arttikca artan herhangi bir fonksiyon rahatca entropi fonsiyonu olabilir Ornegin bir bardak suyumuz oldugunu ve bunun icine bir damla murekkep damlatip gozledigimizi dusunelim ve iceride neler oldugunu hayal etmeye calisalim Murekkep molekulleri baslangicta kisa bir sure bir arada beklestikten sonra su icine dagilmaya baslayacaklardir Cunku kendilerine carpan su molekulleri tarafindan degisik yonlere itileceklerdir su ve murekkep maddelerinin kimyasal baglarinin birbirlerini itmeye elverisli olmalarindan dolayi Simdi de olaganustu bir bilgisayarin sistemin butun mumkun durumlarini sayabildigini dusunelim Sistemin bir durumu denildiginde anlamamiz gereken sey bir molekulun belirli bir koordinata ve belirli bir hiza bir baska molekulun bir baska belirli koordinata ve hiza sahip oldugu konfigurasyondur Bardaktaki murekkep orneginde bu tur durumlarin sayisinin cok fazla oldugu aciktir Zira bunlarin cok buyuk bir kismi murekkebin molekullerinin bardak icinde oraya buraya rastgele dagildigi duzensiz yani yuksek entropili durumlara karsilik gelirler Bizim algiladigimiz duzeyde bunlarin hepsi homojen durumlardir Cunku karisima baktigimizda o molekulun burada bir baskasinin surada olmasina aldirmadan murekkebin homojen olarak dagildigini soyleyebiliriz Yani olaganustu sayida farkli mikroskopik durum tek bir makroskobik duruma yani homojen duruma karsilik gelir Aslinda sistemler bozulmamakta enerji degisimi bazinda en kararli hali almaya calismaktadirlar Hayatin anlami da budur yasam entropi yollarindan biridir sekerin caya cok daha cabuk karismasini saglayan kasik islevindedir Kapali bir sistemde entropi her zaman artar Kapali sistem kismi cok onemlidir Sisteme enerji vermek suretiyle entropisi azaltilabilir Dunya kapali bir sistem degildir Gunes ten surekli olarak enerji akmaktadir ve duzeni bu saglar Parcacik sayisi sonsuza giderken olmasi en muhtemel olan sey olur Havaya bir miktar bozuk para atilsa hepsinin tura gelme ihtimali yalnizca birdir Biri disinda hepsinin tura gelme ihtimali daha coktur Yarisinin yazi yarisinin tura gelme ihtimali daha da coktur Iste bu sonuncusu maksimum entropiye sahip olan sistemdir Sonuc olarak entropinin artmasi sistemin muhtemel olmayan durumdan daha cok muhtemel olan duruma dogru gitmesi demektir Icinde bulunulan odadaki molekullerin hepsinin odanin sag kosesindeki bir noktaya toplanmasi mumkunse de bu kosulu saglayan yalnizca bir konfigurasyon vardir Oysa atomlarin odanin her yerine esit dagildigi daha cok konfigurasyon vardir Ucuncu kanun Ucuncu yasa su sekildedir Sicaklik mutlak sifira yaklastikca en duragan halindeki bir elementin kusursuz bir kristalinin entropisi de sifira yaklasir Bu durum istatistiksel bir bakis acisiyla bir sistemdeki duzenin veya rastgeleligin seviyesini belirleyen mutlak bir entropi olcegi olusturulmasina imkan verir Bu yasa neden bir maddeyi mutlak sifira kadar sogutmanin imkansiz oldugunu izah eder kaynak belirtilmeli zira sicaklik mutlak sifira yaklastikca hareketlilik miktari da sifira yaklasir Sicaklik mutlak sifira yaklastikca bir sistemin entropisi bir sabite yaklasir Bu sayinin sifir degil de bir sabit olmasinin sebebi butun hareketler durmasina ve buna bagli olan belirsizliklerin yok olmasina ragmen kristal olmayan maddelerin molekuler dizilimlerinin farkli olmasindan kaynaklanan bir belirsizligin hala mevcut olmasidir Ayrica ucuncu yasa sayesinde maddelerin mutlak sifirdaki entropileri referans alinmak uzere kimyasal tepkimelerin incelenmesinde cok yararli olan mutlak entropi tanimlanabilir Alintilar Bu evde termodinamik kurallarina uyariz Lisa enerjisi zamanla artan bir devridaim makinasi yaptiktan sonra Homer Simpson Termodinamik komik bir konudur Ilk defa ogrendiginizde ne oldugunu anlamazsiniz bile Ikinci defa uzerinden gectiginizde bir iki nokta haric anladiginizi dusunursunuz Ucuncu defa baktiginizda ise anlamadiginizi bilirsiniz ama o zamana kadar konuya alistiginiz icin bu sizi o kadar rahatsiz etmez Arnold Sommerfeld Dokulen sutun arkasindan aglamayin Evren in butun kuvvetleri sutu dokmeyi aklina koymustu bir kez Wikimedia Commons ta Termodinamik ile ilgili ortam dosyalari bulunmaktadir Kaynakca Thermodynamics HTML Ingilizce Britannica 29 Nisan 2015 tarihinde kaynagindan Erisim tarihi 5 Mart 2015 a b c d e f Kaynak hatasi Gecersiz lt ref gt etiketi Britannica isimli refler icin metin saglanmadi Bkz Kaynak gosterme
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans