Topolojik Uzaylar

Topolojik uzaylar, matematiğin Topoloji dalının başlıca uğraş konularıdır. Bir X kümesi ve bu kümenin alt kümelerinin bir kısmını içeren ve aşağıdaki varsayımları sağlayan S kümesinden oluşurlar:

1) ${\displaystyle \emptyset }$ ve X kümeleri S'nin elemanıdır;

2) S'nin elemanları arasından seçilecek herhangi bir ${\displaystyle U_{\alpha }}$ koleksiyonu için, ${\displaystyle \bigcup _{\alpha }U_{\alpha }}$ kümesi de S'nin bir elemanıdır,

3) S'nin elemanları arasından seçtiğimiz ${\displaystyle U_{1},...,U_{n}}$ kümelerinin olan ${\displaystyle \bigcap _{i=1}^{n}U_{i}}$ kümesi de S'nin elemanıdır.

Burada ikinci şartta bahsettiğimiz koleksiyonun sonsuz sayıda eleman içerebileceğine ancak üçüncü şarttaki altkümelerin sayısının sonlu olduğuna dikkat etmek gereklidir.

Geleneksel olarak X'in altkümelerinden S'nin elemanı olanlara açık kümeler denir. Buna karşılık C kümesi X'in bir altkümesiyse ve de ${\displaystyle X\setminus C}$ fark kümesi açık bir kümeyse, o zaman C'ye de kapalı bir küme denir. Bu tanıma göre X ve ${\displaystyle \emptyset }$ kümeleri aynı zamanda hem açık hem kapalıdırlar.

Verilen bir (X,S) topolojik uzayında X'in altkümelerinden oluşan öyle bir Y kümesi olsun ki X'te açık her küme Y'nin elemanlarının bir birleşimi olarak yazılabilsin. Bu durumda Y kümesine (X,S) uzayının temeli denir.

Örnekler

1) Verilen herhangi bir X kümesi için, S, X'in tüm alt kümelerinin kümesi olsun (yani her bir altküme açık olsun). Böyle oluşturulmuş topolojiye denir.

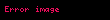
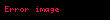
2) Reel Sayılar üzerinde (a,b) şeklindeki (a ${\displaystyle -\infty }$ ve b ${\displaystyle \infty }$ olabilir) doğru parçalarının yarattığı topoloji. 'nın geometrik özelliklerini anlamakta kullanılan doğal topolojidir.

3) Uzunluk uzayları, metrik uzaylar, iç çarpım uzayları ve Banach uzayları topolojik uzaylardır.

Açık Kümeler Kullanılarak Tanımı

X herhangi bir küme, T ise X kümesinin altkümelerinin bir kısmından oluşan bir küme olsun. Eğer T aşağıdaki koşulları sağlıyorsa T'ye X'in üzerinde bir topoloji denir:

1. Boşküme ve X, T'nin elemanları olmalıdır.
2. T'nin herhangi sayıda elemanının (X'in altkümesi olarak) birleşimi yine T'nin elemanı olmalıdır.
3. T'nin sonlu sayıda elemanının kesişimi yine T'nin elemanı olmalıdır.

Bu koşulların sağlanması durumunda T ile donatılmış X kümesine bir topolojik uzay denir.

Örnekler

1. X = {1, 2, 3, 4} ve yularıdaki aksiyomları sağlamak adına Xin yalnız 2 altkümesini içeren koleksiyon τ = {{}, {1, 2, 3, 4}}, X üzerinde bir topolojidir.
2. X = {1, 2, 3, 4} ve X'in altı altkümesinden meydana gelen koleksiyon τ = {{}, {2}, {1, 2}, {2, 3}, {1, 2, 3}, {1, 2, 3, 4}}, X için bir başka topolojidir. (aşikar (indiskrit) topoloji)
3. X = {1, 2, 3, 4} ve koleksiyon τ = P(X) (X'in kuvvet kümesi) verilmiş olsun. (X, τ) bir topolojik uzay temsil eder. Bu durumda τ'ye ayrık topoloji denir.
4. X = Z, (Z : tam sayılar kümesi) ve τ koleksiyonu, Z'nin elemanları ile oluşturulabilecek sonlu sayıdaki tüm altkümeler ve Z'nin kendisinden oluşmak üzere, τ koleksiyonu bir topoloji değildir, çünkü (örneğin) 0'ı içermeyen tüm sonlu altkümelerin birleşimi sonsuzdur, fakat hâlâ Z'nin tüm elemanlarını içermez, bu yüzden τ'nin elemanı değildir.

Ayrıca bakınız

Topoloji Kompakt Uzay Manifold Cebirsel topoloji Diferansiyel topoloji Uzay (matematik)