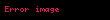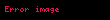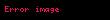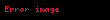Z dönüşümü, matematikte ve sinyal işlemede bir dönüşüm. Zaman tanım kümesinde gerçel ve sanal bileşenleri olan herhangi bir ayrık işareti, frekans tanım kümesindeki biçimine dönüştürür.
Tanım
Dönüşüm şu şekildedir:
Yukarıdaki bağıntıda, n'ler tam sayı ve küçük z'ler karmaşık sayıdır.
Bu ikinci bağıntıya göre ise A, z'nin genliği, φ de fazı ya da argümanı olarak tanımlanır. Faz, radyan'la ölçülür.
Fourier dönüşümü ile ilişkisi
Ayrık zamanlı Fourier dönüşümü (DTFT)'in genelleştirilmesi olan z-dönüşümünün Fourier dönüşümü ile yakından ilgisi vardır. 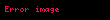
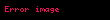
ROC, z Dönüşümünün en önemli kavramıdır. ROC (region of convergence-yakınsama bölgesi) bir sinyalin z-dönüşümünün sonsuz olmayan bir sayıya yakınsadığı değerlerinin z-düzlemi üzerinde gösterildiği alandır. ROC sistem hakkında birçok bilgi almamızı sağlar. Çizimi ise aşağıdaki özelliklere bakılarak yapılır.
ROC bir halka ya da bir disktir ve merkezi orjindedir. H(z)'de z yerine 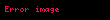
x[n] sınırlı dizi ise ROC bütün z-düzlemidir. Belki 0'ı ya da sonsuzu içermeyebilir.
Nedensel sistemlerde, x[n] sağa yaslıdır ve ROC en dıştaki kutbun dışına doğru olur. Nedensel olmayan sistemlerde, x[n] sola yaslı ve ROC en içteki kutbun içine doğru olur. x[n] hem nedensel hem de anti-nedensel terimler içeriyorsa, ROC en dıştaki kutuptan içeri en içteki kutuptan dışarı doğru olan bir halkadır.
Sistemin hem nedensel hem de kararlı olması durumunda, bütün kutuplar birim çemberin içinde olmalıdır. Çünkü eğer bir kutup bile birim çemberin dışında olsa, nedensel sistem özelliğinden dolayı ROC en sağdaki kutbun dışına doğru olur ve birim çemberi içeremez, bu durumda sistemin kararlılık kriteri de karşılanamaz.
ROC olmak zorundadır.
Bazı Z-dönüşümü çiftleri
Aşağıdaki tabloda bazı sistemlerin z dönüşümleri verilmiştir.
Dirac delta fonksiyonu ve Heaviside birim basamak fonksiyonu aşağıdaki gibi tanımlanır:
Sinyal, 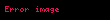 | Z-dönüşümü,  | ROC | |
|---|---|---|---|
| 1 |  |  | 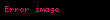 |
| 2 | 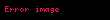 | 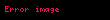 |  |
| 3 |  | 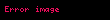 |  |
| 4 | 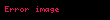 |  |  |
| 5 | 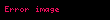 | 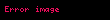 | 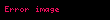 |
| 6 | 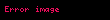 | 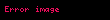 |  |
| 7 | 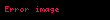 | 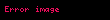 | 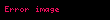 |
| 8 |  | 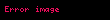 |  |
| 9 | 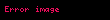 | 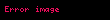 | 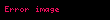 |
| 10 | 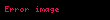 | 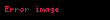 |  |
| 11 | 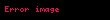 | 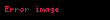 | 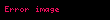 |
| 12 | 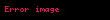 | 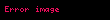 | 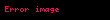 |
| 13 | 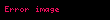 | 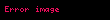 | 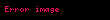 |
| 14 | 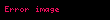 | 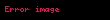 | 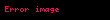 |
| 15 |  | 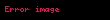 | 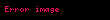 |
| 16 |  |  | 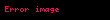 |
| 17 |  |  | 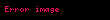 |
| 18 |  | 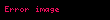 |  |
| 19 | 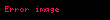 |  |  |
| 20 | 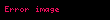 | 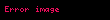 | 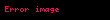 |
| 21 |  | 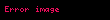 | 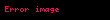 |
Özellikler
| zaman bölgesi | Z- bölgesi | İspat | ROC | |
|---|---|---|---|---|
| Notasyon | 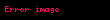 |  | ROC:  | |
| Doğrusallık |  |  |  | En azından ROC1 ve ROC2 bölgelerinin kesişimi |
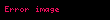
|  | R^{1/k} | ||
| Zamanda kayma | 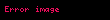 | 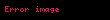 | 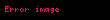 | ROC, eğer  ise dışında ise dışında  ve eğer ve eğer  ise ise  dışında dışında |
| Scaling in the z-domain | 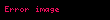 | 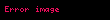 | 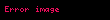 |  |
| Time reversal |  | 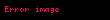 | 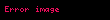 |  |
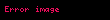 |  | 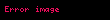 | ROC | |
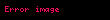 |  | ROC | ||
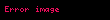 | 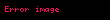 | ROC | ||
| Türev |  |  |  | ROC |
 | 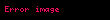 |  | en azından ROC1 ve ROC2 keşisim kümesi | |
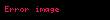 | 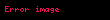 | en azından X1(z)'e ait ROC ve X2( )'e ait ROC'un keşisimi. )'e ait ROC'un keşisimi. | ||
| First Difference |  | 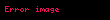 | En azından X1(z) ve 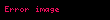 keşisimi keşisimi | |
| Accumulation | 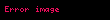 | 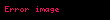 |  | |
| Çarpma |  |  | - | |
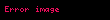 | 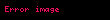 |
, Eğer
nedensel ise.
, Sadece kutuplar
birim çemberin içindeyse.
Ayrıca bakınız
Kaynakça
- ^ "Arşivlenmiş kopya". 5 Ağustos 2011 tarihinde kaynağından . Erişim tarihi: 3 Eylül 2011.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Z donusumu matematikte ve sinyal islemede bir donusum Zaman tanim kumesinde gercel ve sanal bilesenleri olan herhangi bir ayrik isareti frekans tanim kumesindeki bicimine donusturur TanimDonusum su sekildedir X z Z x n n x n z n displaystyle X z mathcal Z x n sum n infty infty x n z n Yukaridaki bagintida n ler tam sayi ve kucuk z ler karmasik sayidir z Aejf A cos f jsin f displaystyle z Ae j varphi A cos varphi j sin varphi Bu ikinci bagintiya gore ise A z nin genligi f de fazi ya da argumani olarak tanimlanir Faz radyan la olculur Fourier donusumu ile iliskisiAyrik zamanli Fourier donusumu DTFT in genellestirilmesi olan z donusumunun Fourier donusumu ile yakindan ilgisi vardir z ejw displaystyle z e j omega gibi dusunulurse DTFT elde edilmektedir Bunun sebebi soyle aciklanmaktadir z bir kompleks sayidir ve kutupsal formda Aejf displaystyle Ae j varphi olarak gosterilmektedir Eger A 1 ise z donusumu Fourier donusumu olmaktadir ama yaricap 1 den farkli ise o zaman z donusumu olarak kalmaktadir ROC z Donusumunun en onemli kavramidir ROC region of convergence yakinsama bolgesi bir sinyalin z donusumunun sonsuz olmayan bir sayiya yakinsadigi degerlerinin z duzlemi uzerinde gosterildigi alandir ROC sistem hakkinda bircok bilgi almamizi saglar Cizimi ise asagidaki ozelliklere bakilarak yapilir ROC bir halka ya da bir disktir ve merkezi orjindedir H z de z yerine z ejw displaystyle z e j omega koyulunca Fourier donusumune yakinsayabilmesi icin ROC un birim cemberi icermesi gerekir Bu ayni zamanda sistemin kararlilik kriteridir ROC kutup iceremez x n sinirli dizi ise ROC butun z duzlemidir Belki 0 i ya da sonsuzu icermeyebilir Nedensel sistemlerde x n saga yaslidir ve ROC en distaki kutbun disina dogru olur Nedensel olmayan sistemlerde x n sola yasli ve ROC en icteki kutbun icine dogru olur x n hem nedensel hem de anti nedensel terimler iceriyorsa ROC en distaki kutuptan iceri en icteki kutuptan disari dogru olan bir halkadir Sistemin hem nedensel hem de kararli olmasi durumunda butun kutuplar birim cemberin icinde olmalidir Cunku eger bir kutup bile birim cemberin disinda olsa nedensel sistem ozelliginden dolayi ROC en sagdaki kutbun disina dogru olur ve birim cemberi iceremez bu durumda sistemin kararlilik kriteri de karsilanamaz ROC olmak zorundadir Bazi Z donusumu ciftleriAsagidaki tabloda bazi sistemlerin z donusumleri verilmistir Dirac delta fonksiyonu ve Heaviside birim basamak fonksiyonu asagidaki gibi tanimlanir u n 1 n 00 n lt 0 displaystyle u n begin cases 1 amp n geq 0 0 amp n lt 0 end cases d n 1 n 00 n 0 displaystyle delta n begin cases 1 amp n 0 0 amp n neq 0 end cases Sinyal x n displaystyle x n Z donusumu X z displaystyle X z ROC1 d n displaystyle delta n 1 displaystyle 1 all z displaystyle mbox all z 2 d n n0 displaystyle delta n n 0 z n0 displaystyle z n 0 z 0 displaystyle z neq 0 3 u n displaystyle u n 11 z 1 displaystyle frac 1 1 z 1 z gt 1 displaystyle z gt 1 4 e anu n displaystyle e alpha n u n 11 e az 1 displaystyle 1 over 1 e alpha z 1 z gt e a displaystyle z gt e alpha 5 u n 1 displaystyle u n 1 11 z 1 displaystyle frac 1 1 z 1 z lt 1 displaystyle z lt 1 6 nu n displaystyle nu n z 1 1 z 1 2 displaystyle frac z 1 1 z 1 2 z gt 1 displaystyle z gt 1 7 nu n 1 displaystyle nu n 1 z 1 1 z 1 2 displaystyle frac z 1 1 z 1 2 z lt 1 displaystyle z lt 1 8 n2u n displaystyle n 2 u n z 1 1 z 1 1 z 1 3 displaystyle frac z 1 1 z 1 1 z 1 3 z gt 1 displaystyle z gt 1 9 n2u n 1 displaystyle n 2 u n 1 z 1 1 z 1 1 z 1 3 displaystyle frac z 1 1 z 1 1 z 1 3 z lt 1 displaystyle z lt 1 10 n3u n displaystyle n 3 u n z 1 1 4z 1 z 2 1 z 1 4 displaystyle frac z 1 1 4z 1 z 2 1 z 1 4 z gt 1 displaystyle z gt 1 11 n3u n 1 displaystyle n 3 u n 1 z 1 1 4z 1 z 2 1 z 1 4 displaystyle frac z 1 1 4z 1 z 2 1 z 1 4 z lt 1 displaystyle z lt 1 12 anu n displaystyle a n u n 11 az 1 displaystyle frac 1 1 az 1 z gt a displaystyle z gt a 13 anu n 1 displaystyle a n u n 1 11 az 1 displaystyle frac 1 1 az 1 z lt a displaystyle z lt a 14 nanu n displaystyle na n u n az 1 1 az 1 2 displaystyle frac az 1 1 az 1 2 z gt a displaystyle z gt a 15 nanu n 1 displaystyle na n u n 1 az 1 1 az 1 2 displaystyle frac az 1 1 az 1 2 z lt a displaystyle z lt a 16 n2anu n displaystyle n 2 a n u n az 1 1 az 1 1 az 1 3 displaystyle frac az 1 1 az 1 1 az 1 3 z gt a displaystyle z gt a 17 n2anu n 1 displaystyle n 2 a n u n 1 az 1 1 az 1 1 az 1 3 displaystyle frac az 1 1 az 1 1 az 1 3 z lt a displaystyle z lt a 18 cos w0n u n displaystyle cos omega 0 n u n 1 z 1cos w0 1 2z 1cos w0 z 2 displaystyle frac 1 z 1 cos omega 0 1 2z 1 cos omega 0 z 2 z gt 1 displaystyle z gt 1 19 sin w0n u n displaystyle sin omega 0 n u n z 1sin w0 1 2z 1cos w0 z 2 displaystyle frac z 1 sin omega 0 1 2z 1 cos omega 0 z 2 z gt 1 displaystyle z gt 1 20 ancos w0n u n displaystyle a n cos omega 0 n u n 1 az 1cos w0 1 2az 1cos w0 a2z 2 displaystyle frac 1 az 1 cos omega 0 1 2az 1 cos omega 0 a 2 z 2 z gt a displaystyle z gt a 21 ansin w0n u n displaystyle a n sin omega 0 n u n az 1sin w0 1 2az 1cos w0 a2z 2 displaystyle frac az 1 sin omega 0 1 2az 1 cos omega 0 a 2 z 2 z gt a displaystyle z gt a OzelliklerZ donusumunun ozellikleri zaman bolgesi Z bolgesi Ispat ROCNotasyon x n Z 1 X z displaystyle x n mathcal Z 1 X z X z Z x n displaystyle X z mathcal Z x n ROC r2 lt z lt r1 displaystyle r 2 lt z lt r 1 Dogrusallik a1x1 n a2x2 n displaystyle a 1 x 1 n a 2 x 2 n a1X1 z a2X2 z displaystyle a 1 X 1 z a 2 X 2 z X z n a1x1 n a2x2 n z n a1 n x1 n z n a2 n x2 n z n a1X1 z a2X2 z displaystyle begin array lcl X z amp amp sum n infty infty a 1 x 1 n a 2 x 2 n z n amp amp a 1 sum n infty infty x 1 n z n a 2 sum n infty infty x 2 n z n amp amp a 1 X 1 z a 2 X 2 z end array En azindan ROC1 ve ROC2 bolgelerinin kesisimix k n x r n rk0 n rk displaystyle x k n begin cases x r amp n rk 0 amp n not rk end cases r displaystyle r tam sayi X zk displaystyle X z k R 1 k Zamanda kayma x n k displaystyle x n k z kX z displaystyle z k X z Z x n k n 0 x n k z n let j n k j k x j z j k j k x j z jz k z k j k x j z j z k j 0 x j z j since x b 0 if b lt 0 z kX z displaystyle begin array lcl Z x n k amp amp sum n 0 infty x n k z n text let j n k amp amp sum j k infty x j z j k amp amp sum j k infty x j z j z k amp amp z k sum j k infty x j z j amp amp z k sum j 0 infty x j z j text since x beta 0 text if beta lt 0 amp amp z k X z end array ROC eger k gt 0 displaystyle k gt 0 ise disinda z 0 displaystyle z 0 ve eger k lt 0 displaystyle k lt 0 ise z displaystyle z infty disindaScaling in the z domain anx n displaystyle a n x n X a 1z displaystyle X a 1 z Z anx n n anx n z n n x n a 1z n X a 1z displaystyle begin array lcl Z a n x n amp amp sum n infty infty a n x n z n amp amp sum n infty infty x n a 1 z n amp amp X a 1 z end array a r2 lt z lt a r1 displaystyle a r 2 lt z lt a r 1 Time reversal x n displaystyle x n X z 1 displaystyle X z 1 Z x n n x n z n m x m zm m x m z 1 m X z 1 displaystyle begin array lcl mathcal Z x n amp amp sum n infty infty x n z n amp amp sum m infty infty x m z m amp amp sum m infty infty x m z 1 m amp amp X z 1 end array 1r1 lt z lt 1r2 displaystyle frac 1 r 1 lt z lt frac 1 r 2 x n displaystyle x n X z displaystyle X z Z x n n x n z n n x n z n n x n z n X z displaystyle begin array lcl Z x n amp amp sum n infty infty x n z n amp amp sum n infty infty x n z n amp amp sum n infty infty x n z n amp amp X z end array ROCRe x n displaystyle operatorname Re x n 12 X z X z displaystyle frac 1 2 left X z X z right ROCIm x n displaystyle operatorname Im x n 12j X z X z displaystyle frac 1 2j left X z X z right ROCTurev nx n displaystyle nx n zdX z dz displaystyle z frac dX z dz Z nx n n nx n z n z n nx n z n 1 z n x n nz n 1 z n x n ddz z n zdX z dz displaystyle begin array lcl Z nx n amp amp sum n infty infty nx n z n amp amp z sum n infty infty nx n z n 1 amp amp z sum n infty infty x n nz n 1 amp amp z sum n infty infty x n frac d dz z n amp amp z frac dX z dz end array ROCx1 n x2 n displaystyle x 1 n x 2 n X1 z X2 z displaystyle X 1 z X 2 z Z x1 n x2 n Z l x1 l x2 n l n l x1 l x2 n l z n l x1 l n x2 n l z n l x1 l z l n x2 n z n X1 z X2 z displaystyle begin array lcl mathcal Z x 1 n x 2 n amp amp mathcal Z sum l infty infty x 1 l x 2 n l amp amp sum n infty infty sum l infty infty x 1 l x 2 n l z n amp amp sum l infty infty x 1 l sum n infty infty x 2 n l z n amp amp sum l infty infty x 1 l z l sum n infty infty x 2 n z n amp amp X 1 z X 2 z end array en azindan ROC1 ve ROC2 kesisim kumesirx1 x2 l x1 l x2 l displaystyle r x 1 x 2 l x 1 l x 2 l Rx1 x2 z X1 z X2 z 1 displaystyle R x 1 x 2 z X 1 z X 2 z 1 en azindan X1 z e ait ROC ve X2 z 1 displaystyle z 1 e ait ROC un kesisimi First Difference x n x n 1 displaystyle x n x n 1 1 z 1 X z displaystyle 1 z 1 X z displaystyle En azindan X1 z ve z gt 0 displaystyle z gt 0 kesisimiAccumulation k nx k displaystyle sum k infty n x k 11 z 1X z displaystyle frac 1 1 z 1 X z n k nx k z n n x n x n 1 x n 2 x z n X z 1 z 1 z 2 z 3 X z j 0 z j X z 11 z 1 displaystyle begin array lcl sum n infty infty sum k infty n x k cdot z n sum n infty infty x n x n 1 x n 2 cdots x infty z n X z 1 z 1 z 2 z 3 cdots X z sum j 0 infty z j X z frac 1 1 z 1 end array Carpma x1 n x2 n displaystyle x 1 n x 2 n 1j2p CX1 v X2 zv v 1dv displaystyle frac 1 j2 pi oint C X 1 v X 2 frac z v v 1 mathrm d v n x1 n x2 n displaystyle sum n infty infty x 1 n x 2 n 1j2p CX1 v X2 1v v 1dv displaystyle frac 1 j2 pi oint C X 1 v X 2 frac 1 v v 1 mathrm d v x 0 limz X z displaystyle x 0 lim z rightarrow infty X z Eger x n displaystyle x n nedensel ise dd Son deger teoremix limz 1 z 1 X z displaystyle x infty lim z rightarrow 1 z 1 X z Sadece kutuplar z 1 X z displaystyle z 1 X z birim cemberin icindeyse dd Ayrica bakinizMatematiksel fonksiyonlarin listesi Fourier donusumu Laplace donusumu Hankel donusumuKaynakca Arsivlenmis kopya 5 Agustos 2011 tarihinde kaynagindan Erisim tarihi 3 Eylul 2011
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans