Kuantum harmonik salınıcı, klasik harmonik salınıcın benzeşiğidir. Rastgele seçilmiş potansiyeli denge noktası civarında harmonik potansiyele yakınsanabildiğinden nicem mekanğindeki en önemli model sistemlerden biridir. Dahası, nicem mekaniğinde kesin analitik çözümü olan çok az sistemden biridir.
Tek boyutlu harmonik salınıcı


Hamilton İşlevi ve Enerji Özdurumu
Parçacığın Hamilton işlevi (bir sistemin enerjisini momentumu ve konumuna bağlı olarak ifade etmeye yarayan işlev):
m parçacığın kütlesi, ω açısal frekansı, 
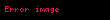
Hamilton işlevindeki ilk ifade parçacığın olası hareket (kinetik) enerjisidir ve ikinci terim sırasıyla potansiyel enerji durumunu ifade eder. Zamandan bağımsız Schrödinger eşitliği;
Yine de E zamandan bağımsız olan enerji düzeyini ve gerçek bir sayıyı ifade eder öz değeri olarak adlandırılabilir ve çözüm |ψ⟩ özdurumdaki enerji düzeyini gösterir.Öz değerinin eşitliği koordinat kökeninde dalga işlevi, ⟨x|ψ⟩ = ψ(x), bulmak için spektral yöntem kullanılarak türetilebilir. Görülür ki, çözümleri aynı kümedendir. Bu yöntem, miktarları;
Hn işlevleri Hermit polinomlarını ifade eder;
. .
Enerji düzeylerinin eşitliği ise;
. ’dir.
Bu enerji spekturumu üç nedenden dikkat edilmeye değerdir. Öncelikle enerjiler nicelenir, yani sadece ayrık enerji değerleri mümkündür (tam sayı ve yarısının toplamı ile ħω’ın çarpımı); bu nicem sistemlerinde, parçacık sınırlandığındaki sistemlerin genel özelliğidir. İkinci olarak, bu ayrık enerji düzeylerinde eşit olarak boşluk bırakılır, Bohr atom modelinin aksine ya da kutudaki parçacık gibi. Üçüncü olarak, ulaşılabilen en düşük enerji (n = 0 durumu, zemin durumu) potansiyel enerjiden büyüktür ancak hw/2’den küçüktür bu duruma sıfır noktası enerjisi denir. Heisenberg’ün belirsizlik ilkesine göre sıfır noktası enerjisi yüzünden, salınıcının zemin noktasındaki konumu ve momentumu klasik salınıcıda olduğu gibi düzgün değildir, ama dağılım çeşitliliği azdır. Sıfır noktası enerjisinin nicem alan kuramı ve nicem kütleçekimi içinde oldukça büyük önemi vardır. Zemin durumu olası özkütlesinin sıfır noktasında yoğunlaşması dikkate alınması gereken bir durumdur. Bu parçacığın beklendiği gibi düşük bir enerji ile zamanının çoğunu potansiyel kuyusunun dibinde geçirdiği anlamına gelir. Enerjinin artması ile birlikte, olası özkütle enerjinin potansiyel enerji ile uyuştuğu klasik dönüm noktalarında yoğunlaşır. Bu klasik harmonik salınıcı ile tutarlıdır, bunun için parçacık zamanının çoğunu en yavaş olduğu dönüm noktalarında harcar. Bu yüzden karşılanım ilkesi doğrudur.
Yaradış-yokediş işlemcileri yöntemi

Bu spektral yöntem, tekdüze bir yöntem olarak değerlendirilebilir.Paul Dirac tarafından geliştirilen yaradış-yokediş işlemci yöntemi türev denklemini çözmemize gerek kalmadan enerjinin öz değerini bulmamızı sağlar. Dahası, nicem alan kuramındaki birçok karışık problem için genellenebilir.Bu başlangıçtan sonra, işlemcileri a olarak ve a’nın bitiştirilmişi (adjoint), (a†) olarak tanımlıyoruz,
Bu (
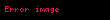
Operator a Hermit işlevi değildir, çünkü kendisi ve bitiştirilmişi eşit değildir. Yine de enerji öz durumu |n⟩, bu yaradış-yokediş işlemcileri tarafından işletildiğinde, şunu verir;
.
Bu a nicemi silerken ’(a†)ın nicem salınıcı için nicemde bir enerjisi olduğunun ispatıdır, bu yüzden, yaradış-yokediş işlemcileri olarak anılırlar. Yukarıdaki ilişkilere göre, sayı işlemcisini de tanımlayabiliriz,N:
.
Bu çeviriciler kolaylıkla kuralsal öndelenim (komütasyon) ilişkilerini elde etmemizi sağlar.,
Hamilton işlemcileri şöyle gösterilebilir;
Yani, enerjinin öz durumu aynı zamanda N’nin öz durumudur. Öndelenim (Komütasyon) özellikleri ;
Ve benzer olarak dir.
Bu şu anlama gelir; a |n⟩’e göre değişir, çarpımsal bir sabit, |n–1⟩, üretmek için ve (a†) |n⟩’e göre değişir, |n+1⟩, sabitini üretmek için değişir. Bu yüzden, a düşürücü işlemci ve (a†) yükseltici işlemcisi olarak da adlandırılır. Bu iki işlemciye yaradış-yokediş işlemcileri de denir. Nicem alan kuramında yaradış-yokediş işlemcileri olarak da adlandırılırlar çünkü enerjinin miktarına göre parçacık yaratıp yok ederler. Daha az enerjiyle başka bir öz durumu yaratmak için düşürücü işlemciyi kullanırız. Bu uygulamayı düşürücü işlemci de takip ederek, E = −∞) ‘a kadar enerji üretebilirmiş gibi gösterebiliriz . Ancak,
En küçük öz sayısı 0’dır ve
..
Bu durumda, düşürücü işlemcinin sonraki uygulamaları öz durumu enerjilerine ek olarak 0’ı üretecektir.
Son olarak, |0⟩ yükseltici işlemciyi ve uygun standartlaştırma faktörlerini çarparak sonsuz sayıda öz durumu enerji setleri üretiriz.
,
örneğin
,
Enerji spektrumu ile uyumludur. Rastgele öz durumu |0⟩ ile şu şekilde ifade edilir,
.
İspat:
|0>’ın Zemin durumu a |0⟩ = 0 olarak gösterilir,
Ve bu yüzden
önceki bölümdeki gibi.
Doğal uzunluk ve enerji ölçekleri
Nicem harmonik salınıcı, uzunluk ve enerji için problem kolaylaştıracak doğal ölçeklere sahiptir. Boyutsuzlaştırmayla bulunabilir. Sonuç bize eğer enerjisini ħω ile mesafeyi √ħ/(mω) ile ölçersek Schrödinger’in denklemi şöyle olur;
Enerji öz değerleri ve işlevleri olurken
Hn(x) Hermit polinomları demektir. Karışıklıktan kaçınmak için, bu makalede “doğal birmler”`i benimsememeliyiz. Ancak bu birimler çoğunlukla hesaplamalarda karışıklığı atlandığından kolay gelir.
Faz-uzayı çözümleri
Nicem mekaniğinin faz-uzayı denklemleştirilmesinde, nicem harmonik salınıcı için olasılık dağılımında birkaç farklı temsili çözümler yazılabilir. En yaygın kullanılanı ise Wigner işlevidir.
Çözümü şöyledir;
Bu örnek bize gösterir ki Wigner-Weyl dönüşümü sayesinde Hermit ve Laguerre polinomları birbiri ile ilişkilidir.
N-boyutlu harmonik salınıcı
Tek boyutlu harmonik salınıcı N-boyutluya kolaylıkla genellenebilir, N=1,2,3,…olabilir. Bir boyutta, parçacığın konumu tek koordinat x ile belirlenebilir. N boyutta ise, bu N koordinat ile yer değişir, x1, ..., xN. Buna göre her konumun momentumunu olduğunu düşünürsek, momentum p1, ..., pN şeklinde gösterilebilir. Bu iki işlemci arasındaki kuralsal değiştirme ilişkisi şöyledir;
.
Sistemin Hamilton işlevi,
.
Bu Hamilton işlevi formunun açıkça gösterdiği gibi, N-boyutlu harmonik salınıcı N tane bağımsız, aynı kütle ve yay sabitine sabit salınıcı ile tamamıyla aynı şeydir. Bu durumda, nicelikler, x1, ..., xN, N tane parçacığın yerini belirtirler. Bu 
Yaradış-yokediş işlemci yönteminde, N tane yaradış-yokediş işlemci serisi belirlenir,
.
Tek-boyutlu duruma göre benzer işlem uygulanırsa, burada da ai ve a†i alçaltan ve yükselten işlemciler diyebiliriz. Hamilton işlevi,
Hamilton işlevi, dinamik eşbakışım(simetri) grubunun altındaki U(N) (boyutların bölünmez grubu) sabit niceliktir, şöyle tanımlanır,
burada 
Sistemlerin enerji düzeyleri
.
Tek-boyutlu durumdaki gibi enerji nicemlenir. Taban durum enerjisi tek boyutlu durum enerjisinin N katıdır, bu benzerliği beklendiği gibi N tane bağımsız tek-boyutlu salınıcı için kullanırız. Bunun dışında bir fark daha vardır tek-boyutlu durumda, tüm enerji düzeyleri farklı bir nicem değeri ifade eder. N-boyutta, zemin durumu hariç, enerji düzeyleri bozulur, bu yüzden bazı durumlarda aynı enerji olur. Çakışıklık (degeneracy) diğer işlemlere oranla kolayca hesaplanabilir. Örnek olarak, 3-boyutlu bir durumu varsayalım: n = n1 + n2 + n3 olarak tanımlayalım. Tüm durumlar aynı n ile eşit enerjiye sahip olur. Bilinen n için, belirli bir n1 seçilir, n2 + n3 = n − n1 ‘dir. n − n1 + 1‘in olası grupları {n2, n3}’dir. n2 0’dan n − e kadar değerler alır ve tüm n2 değerli için n3 ayarlanır. Çakışıklığın (degeneracy) derecesi şöyle hesaplanır.
Genel N ve n için denklem şudur; [gn :
Verilen özel durum N = 3, tamamen bu eşitliği takip edilerek bulunur. Ancak bu sadece fark edilebilir parçacıklar için doğrudur ya da N-boyuttaki bir parçacık için doğrudur. N tane bozon için geçerli durumdaki çakışıklık çizelgesi tam sayıları kullanarak yazıldığında N’den küçük ya da N’e eşittir.
Bu durum N nicemini 

Örnek: 3D izotropik harmonik salınıcı
Küresel eşbakışımlı üç boyutlu harmonik salınıcı Scrödinger eşitliği değerlerin ayrılığı ile açıkça çözülebilir.Bu işlem, hidrojen-benzeri atom probleminin benzeşiğidir ve küresel eşbakışımlı potansiyeli ile,


birimboylandırım sabitidir.
Laguerre polinomu olarak genellenebilirler. k negatif olmayan bir tam sayıdır.
küresel harmonik işlevi.
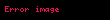

Enerji genelde tek bir nicem sayısıyla ifade edilir.
Çünkü k tüm 


‘dir.
n’in çift ya da tek olmasına göre toplam 0 ya da 1’den başlar. Bu sonuç üsteki boyut denklemine göre ve SU(3)’ün eşbakışımlı temsili ile ilgili çakışıklık grubudur.
Harmonik salınıcı kafesi: fononlar
Harmonik salınıcı görüşünü birçok parçacığın kafesi olarak genişletebiliriz. Tek boyutlu nicem mekanik harmonik zincirinde N tane özdeş atom ele alınır. Bu kafesin en basit nicem mekaniksel modelidir ve bundan nasıl fononların yayıldığını görürüz. Bu model için gelişecek olan biçim iki ve üç boyutlu olarak genellenebilir. Bundan önceki bölümde, denge konumlarına göre ölçüm yaparak kütlelerin konumları olan 


m, her atomun ayrı kütlesi (hepsinin eşit olduğunu var sayılır) ve i. atom için ve en yakın komşuları için (nn) 



Genel olarak
Potansiyel enerji şöyle gösterilebilir;
Hamilton işlevi dalgayöneyli olarak şöyle yazılabilir;
Konum değerleri arasındaki bağlantı dikkate alınacak bir dönüşüme uğramıştır; Eğer Qlar ve Πler hermitian(değiller) olsalar, dönüşmüş Hamilton işlevi N eşlememiş harmonik salınıcıya eşit olur. Kolaylık için, sınır durumunu periyoduk olarak belirleriz, atomun (N+1). Eşitliği ilk atoma eşittir. Fiziksel olarak, bu zincirin sonuna eklenir. Sonuç veren nicelik
Üst düzey bağ n en az (minimum) dalga boyundan gelir, yukarıda tartışıldığı gibi kafes boşluğu, a,`nın ik katıdır. Harmonik salınıcının öz değeri ya da 
Eğer sıfır noktası enerjisini yoksayarsak düzeyler şöyle sıralanır: ħω, 2ħω, 3ħω, ...
- ħω, 2ħω, 3ħω, ...
ħω’ ħωnin gerçek enerji değeri, sonraki enerji düzeyinin harmonik salınıcı kafesine tedarik edilmelidir. Elektromanyetik alan sayısal olarak belirlendiğinde foton durumunun kıyasında titreşim enerjisinin nicemine fonon denir. Tüm nicem sistemleri dalgamsı ya da parçacığımsı özellik gösterirler. Fononun parçacığımsı özellikleri ikinci nicelemede en iyi anlaşılır ve işlemci teknikleri sonra tanımlanır.
Uygulamaları
- Çift atomlu molekülün titreşimi iki cisimli nicem harmonik salınıcına örnektir. Açısal tekrarsıklığı şöyle bulunur,
- :
indirgenmiş kütledir ve = m1m2/(m1+m²) olarak iki atomun kütlesi ile ilişkilidir.
- Hooke’un atomu basit bir helyum atom modelidir nicem harmonik salınıcında da kullanılır.
- Üstte tartışılan model fononlar,
- Kütle ve yükün değişmeyen manyetik alanda olması açısal momentumlu tek boyutlu nicem harmonik salınıcına ya da iki boyutlu nicem harmonik salınıcına bir örnektir.
Kaynakça
İngilizce vikipedi
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Kuantum harmonik salinici klasik harmonik salinicin benzesigidir Rastgele secilmis potansiyeli denge noktasi civarinda harmonik potansiyele yakinsanabildiginden nicem mekangindeki en onemli model sistemlerden biridir Dahasi nicem mekaniginde kesin analitik cozumu olan cok az sistemden biridir Tek boyutlu harmonik salinici Ilk sekiz bagli ozdurumlar icin dalga fonksiyonu gosterimleri n 0 dan 7 ye dir Yatay eksen x konumunu gosterir Not grafikler normalize degildir ve bazi fonksiyonlarin isaretleri metinde verilenlerden farklidir Karsilayan olasilik yogunlugu Hamilton Islevi ve Enerji OzdurumuParcacigin Hamilton islevi bir sistemin enerjisini momentumu ve konumuna bagli olarak ifade etmeye yarayan islev H p 22m 12mw2x 2 displaystyle hat H frac hat p 2 2m frac 1 2 m omega 2 hat x 2 m parcacigin kutlesi w acisal frekansi x x displaystyle hat x x konum islemcisi ve p displaystyle hat p momentum islemcisidir Momentum islemcisi ise su denklemle bulunur p iℏ x displaystyle hat p i hbar partial over partial x Hamilton islevindeki ilk ifade parcacigin olasi hareket kinetik enerjisidir ve ikinci terim sirasiyla potansiyel enerji durumunu ifade eder Zamandan bagimsiz Schrodinger esitligi H ps E ps displaystyle hat H left psi right rangle E left psi right rangle Yine de E zamandan bagimsiz olan enerji duzeyini ve gercek bir sayiyi ifade eder oz degeri olarak adlandirilabilir ve cozum ps ozdurumdaki enerji duzeyini gosterir Oz degerinin esitligi koordinat kokeninde dalga islevi x ps ps x bulmak icin spektral yontem kullanilarak turetilebilir Gorulur ki cozumleri ayni kumedendir Bu yontem miktarlari psn x 12nn mwpℏ 1 4 e mwx22ℏ Hn mwℏx n 0 1 2 displaystyle psi n x frac 1 sqrt 2 n n cdot left frac m omega pi hbar right 1 4 cdot e frac m omega x 2 2 hbar cdot H n left sqrt frac m omega hbar x right qquad n 0 1 2 ldots Hn islevleri Hermit polinomlarini ifade eder Hn x 1 nex2dndxn e x2 displaystyle H n x 1 n e x 2 frac d n dx n left e x 2 right Enerji duzeylerinin esitligi ise En ℏw n 12 displaystyle E n hbar omega left n 1 over 2 right dir Bu enerji spekturumu uc nedenden dikkat edilmeye degerdir Oncelikle enerjiler nicelenir yani sadece ayrik enerji degerleri mumkundur tam sayi ve yarisinin toplami ile ħw in carpimi bu nicem sistemlerinde parcacik sinirlandigindaki sistemlerin genel ozelligidir Ikinci olarak bu ayrik enerji duzeylerinde esit olarak bosluk birakilir Bohr atom modelinin aksine ya da kutudaki parcacik gibi Ucuncu olarak ulasilabilen en dusuk enerji n 0 durumu zemin durumu potansiyel enerjiden buyuktur ancak hw 2 den kucuktur bu duruma sifir noktasi enerjisi denir Heisenberg un belirsizlik ilkesine gore sifir noktasi enerjisi yuzunden salinicinin zemin noktasindaki konumu ve momentumu klasik salinicida oldugu gibi duzgun degildir ama dagilim cesitliligi azdir Sifir noktasi enerjisinin nicem alan kurami ve nicem kutlecekimi icinde oldukca buyuk onemi vardir Zemin durumu olasi ozkutlesinin sifir noktasinda yogunlasmasi dikkate alinmasi gereken bir durumdur Bu parcacigin beklendigi gibi dusuk bir enerji ile zamaninin cogunu potansiyel kuyusunun dibinde gecirdigi anlamina gelir Enerjinin artmasi ile birlikte olasi ozkutle enerjinin potansiyel enerji ile uyustugu klasik donum noktalarinda yogunlasir Bu klasik harmonik salinici ile tutarlidir bunun icin parcacik zamaninin cogunu en yavas oldugu donum noktalarinda harcar Bu yuzden karsilanim ilkesi dogrudur Yaradis yokedis islemcileri yontemiAltta zemin durumda n 0 ile baslayan ve uste dogru enerjisi giderek artan bagli ozdurumlar icin olasilik yogunluklari psn x 2 Yatay eksen x i gosterir ve parlak renkler daha yuksek olasilik yogunluklarini temsil eder Bu spektral yontem tekduze bir yontem olarak degerlendirilebilir Paul Dirac tarafindan gelistirilen yaradis yokedis islemci yontemi turev denklemini cozmemize gerek kalmadan enerjinin oz degerini bulmamizi saglar Dahasi nicem alan kuramindaki bircok karisik problem icin genellenebilir Bu baslangictan sonra islemcileri a olarak ve a nin bitistirilmisi adjoint a olarak tanimliyoruz a mw2ℏ x imwp a mw2ℏ x imwp displaystyle begin aligned a amp sqrt m omega over 2 hbar left hat x i over m omega hat p right a dagger amp sqrt m omega over 2 hbar left hat x i over m omega hat p right end aligned Bu x displaystyle hat x ve p displaystyle hat p kullanmamizi saglar x ℏ2mw a a displaystyle hat x sqrt frac hbar 2m omega a a dagger p imwℏ2 a a displaystyle hat p i sqrt frac m omega hbar 2 a dagger a Operator a Hermit islevi degildir cunku kendisi ve bitistirilmisi esit degildir Yine de enerji oz durumu n bu yaradis yokedis islemcileri tarafindan isletildiginde sunu verir a n n 1 n 1 displaystyle a dagger n rangle sqrt n 1 n 1 rangle a n n n 1 displaystyle a n rangle sqrt n n 1 rangle Bu a nicemi silerken a in nicem salinici icin nicemde bir enerjisi oldugunun ispatidir bu yuzden yaradis yokedis islemcileri olarak anilirlar Yukaridaki iliskilere gore sayi islemcisini de tanimlayabiliriz N N a a displaystyle N a dagger a N n n n displaystyle N left n right rangle n left n right rangle Bu ceviriciler kolaylikla kuralsal ondelenim komutasyon iliskilerini elde etmemizi saglar a a 1 N a a N a a displaystyle a a dagger 1 qquad N a dagger a dagger qquad N a a Hamilton islemcileri soyle gosterilebilir H N 12 ℏw displaystyle H left N frac 1 2 right hbar omega Yani enerjinin oz durumu ayni zamanda N nin oz durumudur Ondelenim Komutasyon ozellikleri Na n a N N a n a N a n n 1 a n displaystyle begin aligned Na dagger n rangle amp left a dagger N N a dagger right n rangle amp left a dagger N a dagger right n rangle amp n 1 a dagger n rangle end aligned Ve benzer olarak dir Na n n 1 a n displaystyle Na n rangle n 1 a n rangle Bu su anlama gelir a n e gore degisir carpimsal bir sabit n 1 uretmek icin ve a n e gore degisir n 1 sabitini uretmek icin degisir Bu yuzden a dusurucu islemci ve a yukseltici islemcisi olarak da adlandirilir Bu iki islemciye yaradis yokedis islemcileri de denir Nicem alan kuraminda yaradis yokedis islemcileri olarak da adlandirilirlar cunku enerjinin miktarina gore parcacik yaratip yok ederler Daha az enerjiyle baska bir oz durumu yaratmak icin dusurucu islemciyi kullaniriz Bu uygulamayi dusurucu islemci de takip ederek E a kadar enerji uretebilirmis gibi gosterebiliriz Ancak n n N n n a a n a n a n 0 displaystyle n langle n N n rangle langle n a dagger a n rangle left a n rangle right dagger a n rangle geqslant 0 En kucuk oz sayisi 0 dir ve a 0 0 displaystyle a left 0 right rangle 0 Bu durumda dusurucu islemcinin sonraki uygulamalari oz durumu enerjilerine ek olarak 0 i uretecektir H 0 ℏw2 0 displaystyle H left 0 right rangle frac hbar omega 2 left 0 right rangle Son olarak 0 yukseltici islemciyi ve uygun standartlastirma faktorlerini carparak sonsuz sayida oz durumu enerji setleri uretiriz 0 1 2 n displaystyle left left 0 right rangle left 1 right rangle left 2 right rangle left n right rangle right ornegin H n ℏw n 12 n displaystyle H left n right rangle hbar omega left n frac 1 2 right left n right rangle Enerji spektrumu ile uyumludur Rastgele oz durumu 0 ile su sekilde ifade edilir n a nn 0 displaystyle n rangle frac left a dagger right n sqrt n 0 rangle Ispat n aa n n a a a a n n N 1 n n 1 a n n 1 n 1 n a n n 1 a 2n n 1 n 2 a nn 0 displaystyle begin aligned langle n aa dagger n rangle amp langle n left a a dagger a dagger a right n rangle langle n left N 1 right n rangle n 1 Rightarrow a dagger n rangle amp sqrt n 1 n 1 rangle Rightarrow n rangle amp frac a dagger sqrt n n 1 rangle frac left a dagger right 2 sqrt n n 1 n 2 rangle cdots frac left a dagger right n sqrt n 0 rangle end aligned 0 gt in Zemin durumu a 0 0 olarak gosterilir x a 0 0 x ℏmwddx x 0 0 x 0 mwpℏ 14exp mw2ℏx2 ps0 displaystyle begin aligned amp left langle x left a right 0 right rangle 0 Longrightarrow amp left x frac hbar m omega frac d dx right left langle x 0 right rangle 0 Longrightarrow amp left langle x 0 right rangle left frac m omega pi hbar right frac 1 4 exp left frac m omega 2 hbar x 2 right psi 0 end aligned Ve bu yuzden x a 0 ps1 displaystyle langle x a dagger 0 rangle psi 1 onceki bolumdeki gibi Dogal uzunluk ve enerji olcekleriNicem harmonik salinici uzunluk ve enerji icin problem kolaylastiracak dogal olceklere sahiptir Boyutsuzlastirmayla bulunabilir Sonuc bize eger enerjisini ħw ile mesafeyi ħ mw ile olcersek Schrodinger in denklemi soyle olur H 12d2dx2 12x2 displaystyle H 1 over 2 d 2 over dx 2 1 over 2 x 2 Enerji oz degerleri ve islevleri olurken psn x x n 12nn p 1 4exp x2 2 Hn x displaystyle psi n x equiv left langle x n right rangle 1 over sqrt 2 n n pi 1 4 hbox exp x 2 2 H n x En n 12 displaystyle E n n tfrac 1 2 Hn x Hermit polinomlari demektir Karisikliktan kacinmak icin bu makalede dogal birmler i benimsememeliyiz Ancak bu birimler cogunlukla hesaplamalarda karisikligi atlandigindan kolay gelir Faz uzayi cozumleriNicem mekaniginin faz uzayi denklemlestirilmesinde nicem harmonik salinici icin olasilik dagiliminda birkac farkli temsili cozumler yazilabilir En yaygin kullanilani ise Wigner islevidir Cozumu soyledir Fn u 1 npℏLn 4uℏw e 2u ℏw displaystyle F n u frac 1 n pi hbar L n left 4 frac u hbar omega right e 2u hbar omega u 12mw2x2 p22m displaystyle u frac 1 2 m omega 2 x 2 frac p 2 2m Bu ornek bize gosterir ki Wigner Weyl donusumu sayesinde Hermit ve Laguerre polinomlari birbiri ile iliskilidir N boyutlu harmonik saliniciTek boyutlu harmonik salinici N boyutluya kolaylikla genellenebilir N 1 2 3 olabilir Bir boyutta parcacigin konumu tek koordinat x ile belirlenebilir N boyutta ise bu N koordinat ile yer degisir x1 xN Buna gore her konumun momentumunu oldugunu dusunursek momentum p1 pN seklinde gosterilebilir Bu iki islemci arasindaki kuralsal degistirme iliskisi soyledir xi pj iℏdi j xi xj 0 pi pj 0 displaystyle begin matrix left x i p j right amp amp i hbar delta i j left x i x j right amp amp 0 left p i p j right amp amp 0 end matrix Sistemin Hamilton islevi H i 1N pi22m 12mw2xi2 displaystyle H sum i 1 N left p i 2 over 2m 1 over 2 m omega 2 x i 2 right Bu Hamilton islevi formunun acikca gosterdigi gibi N boyutlu harmonik salinici N tane bagimsiz ayni kutle ve yay sabitine sabit salinici ile tamamiyla ayni seydir Bu durumda nicelikler x1 xN N tane parcacigin yerini belirtirler Bu r2 displaystyle r 2 potansiyelinin potansiyel enerjinin koordinatlara gore ayrilmasini saglayan uygun bir ozelligidir Gozlemler bu cozumu dogrular niteliktedir Belirli nicem sayilari seti icin n N boyutlu salinicinin enerji oz islevleri 1 boyutlu oz islevi gibi ifade edilir x ps n i 1N xi psni displaystyle langle mathbf x psi n rangle prod i 1 N langle x i psi n i rangle Yaradis yokedis islemci yonteminde N tane yaradis yokedis islemci serisi belirlenir ai mw2ℏ xi imwpi ai mw2ℏ xi imwpi displaystyle begin matrix a i amp amp sqrt m omega over 2 hbar left x i i over m omega p i right a i dagger amp amp sqrt m omega over 2 hbar left x i i over m omega p i right end matrix Tek boyutlu duruma gore benzer islem uygulanirsa burada da ai ve a i alcaltan ve yukselten islemciler diyebiliriz Hamilton islevi H ℏw i 1N ai ai 12 displaystyle H hbar omega sum i 1 N left a i dagger a i frac 1 2 right Hamilton islevi dinamik esbakisim simetri grubunun altindaki U N boyutlarin bolunmez grubu sabit niceliktir soyle tanimlanir Uai U j 1Naj Ujifor allU U N displaystyle U a i dagger U dagger sum j 1 N a j dagger U ji quad hbox for all quad U in U N burada Uji displaystyle U ji U N in dizey temsil elementidir Sistemlerin enerji duzeyleri E ℏw n1 nN N2 displaystyle E hbar omega left n 1 cdots n N N over 2 right ni 0 1 2 the energy level in dimension i displaystyle n i 0 1 2 dots quad hbox the energy level in dimension i Tek boyutlu durumdaki gibi enerji nicemlenir Taban durum enerjisi tek boyutlu durum enerjisinin N katidir bu benzerligi beklendigi gibi N tane bagimsiz tek boyutlu salinici icin kullaniriz Bunun disinda bir fark daha vardir tek boyutlu durumda tum enerji duzeyleri farkli bir nicem degeri ifade eder N boyutta zemin durumu haric enerji duzeyleri bozulur bu yuzden bazi durumlarda ayni enerji olur Cakisiklik degeneracy diger islemlere oranla kolayca hesaplanabilir Ornek olarak 3 boyutlu bir durumu varsayalim n n1 n2 n3 olarak tanimlayalim Tum durumlar ayni n ile esit enerjiye sahip olur Bilinen n icin belirli bir n1 secilir n2 n3 n n1 dir n n1 1 in olasi gruplari n2 n3 dir n2 0 dan n e kadar degerler alir ve tum n2 degerli icin n3 ayarlanir Cakisikligin degeneracy derecesi soyle hesaplanir gn n1 0nn n1 1 n 1 n 2 2 displaystyle g n sum n 1 0 n n n 1 1 frac n 1 n 2 2 Genel N ve n icin denklem sudur gn gn N n 1n displaystyle g n binom N n 1 n bolunmez grubun temsili indirgenemez esbakisimli simetrik n inci kuvvetidir Verilen ozel durum N 3 tamamen bu esitligi takip edilerek bulunur Ancak bu sadece fark edilebilir parcaciklar icin dogrudur ya da N boyuttaki bir parcacik icin dogrudur N tane bozon icin gecerli durumdaki cakisiklik cizelgesi tam sayilari kullanarak yazildiginda N den kucuk ya da N e esittir gn p N n displaystyle g n p N n Bu durum N nicemini k 0 knk n displaystyle sum k 0 infty kn k n ve k 0 nk N displaystyle sum k 0 infty n k N sinirlayinca ortaya cikar Ornek 3D izotropik harmonik saliniciKuresel esbakisimli uc boyutlu harmonik salinici Scrodinger esitligi degerlerin ayriligi ile acikca cozulebilir Bu islem hidrojen benzeri atom probleminin benzesigidir ve kuresel esbakisimli potansiyeli ile V r 12mw2r2 displaystyle V r 1 over 2 mu omega 2 r 2 m displaystyle mu problemin kutlesidir Cunku m manyetik nicem sayisi olarak kullanilacak bu yuzden kutle m displaystyle mu ile ifade edilecek Cozum okunur psklm r 8 ϕ Nklrle nr2Lk l 12 2nr2 Ylm 8 ϕ displaystyle psi klm r theta phi N kl r l e nu r 2 L k l 1 over 2 2 nu r 2 Y lm theta phi Nkl 2n3p2k 2l 3k nl 2k 2l 1 displaystyle N kl sqrt sqrt frac 2 nu 3 pi frac 2 k 2l 3 k nu l 2k 2l 1 birimboylandirim sabitidir n mw2ℏ displaystyle nu equiv mu omega over 2 hbar Lk l 12 2nr2 displaystyle L k l 1 over 2 2 nu r 2 Laguerre polinomu olarak genellenebilirler k negatif olmayan bir tam sayidir Ylm 8 ϕ displaystyle Y lm theta phi kuresel harmonik islevi ℏ displaystyle hbar indirgenmis Planck sabiti ℏ h2p displaystyle hbar equiv frac h 2 pi Enerjinin ozdegeri E ℏw 2k l 32 displaystyle E hbar omega left 2k l frac 3 2 right Enerji genelde tek bir nicem sayisiyla ifade edilir n 2k l displaystyle n equiv 2k l Cunku k tum l 0 2 n 2 n displaystyle l 0 2 n 2 n ve l 1 3 n 2 n displaystyle l 1 3 n 2 n degerleri icin negatif olmayan bir tam sayidir Manyetik nicem sayisi m l m l displaystyle l leq m leq l e uyan bir tam sayidir tum n ve l degerleri icin bu yuzden n in bozulma duzeyi l n 2 n 2l 1 n 1 n 2 2 displaystyle sum l ldots n 2 n 2l 1 n 1 n 2 over 2 dir n in cift ya da tek olmasina gore toplam 0 ya da 1 den baslar Bu sonuc usteki boyut denklemine gore ve SU 3 un esbakisimli temsili ile ilgili cakisiklik grubudur Harmonik salinici kafesi fononlarHarmonik salinici gorusunu bircok parcacigin kafesi olarak genisletebiliriz Tek boyutlu nicem mekanik harmonik zincirinde N tane ozdes atom ele alinir Bu kafesin en basit nicem mekaniksel modelidir ve bundan nasil fononlarin yayildigini goruruz Bu model icin gelisecek olan bicim iki ve uc boyutlu olarak genellenebilir Bundan onceki bolumde denge konumlarina gore olcum yaparak kutlelerin konumlari olan x1 x2 displaystyle x 1 x 2 yi bulduk i e xi 0 displaystyle x i 0 eger parcacik denge konumundaysa Iki ya da daha fazla boyutta xi displaystyle x i ler yoneyli degerlerdir Sistemin Hamilton islevi H i 1Npi22m 12mw2 ij nn xi xj 2 displaystyle mathbf H sum i 1 N p i 2 over 2m 1 over 2 m omega 2 sum ij nn x i x j 2 m her atomun ayri kutlesi hepsinin esit oldugunu var sayilir ve i atom icin ve en yakin komsulari icin nn xi displaystyle x i ve pi displaystyle p i konum ve momentum islemcileridir Ancak beklendigi gibi kafeste dalgalar parcacik gibi davrandigi gorunebilir Dalgalarin hareketlerinde dalgayoneyi normal modlari kullanilarak parcaciklarin koordinat degerleri yerine Fourier uzayi ozel olarak islenir Normal modlarin sayilari parcaciklarla aynidir ancak Fourier uzayi sistemin tekrarsikligi icin oldukca kullanislidir N in normal koordinatlar seti Qk displaystyle Q k xs in ayrik Fourier donusumleri olarak tanimlanir ve N eslenik momentumlari P ps nin Fourier donusumleri olarak tanimlanir Qk 1N leikalxl displaystyle Q k 1 over sqrt N sum l e ikal x l Pk 1N le ikalpl displaystyle Pi k 1 over sqrt N sum l e ikal p l kn displaystyle k n fononun dalga numarasidir yani 2 p nin dalga boyuna bolunmesidir Nicelikli degerlerdir cunku atom sayisi sonludur Bu secim istenilen degistirme iliskilerinin gercek bosluk ya da dalgayoneyi uzayini alikoyar xl pm iℏdl m Qk Pk 1N l meikale ik am xl pm iℏN meiam k k iℏdk k Qk Qk Pk Pk 0 displaystyle begin aligned left x l p m right amp i hbar delta l m left Q k Pi k right amp 1 over N sum l m e ikal e ik am x l p m amp i hbar over N sum m e iam left k k right i hbar delta k k left Q k Q k right amp left Pi k Pi k right 0 end aligned Genel olarak lxlxl m 1N kk QkQk leial k k eiamk kQkQ keiamk lpl2 kPkP k displaystyle begin aligned sum l x l x l m amp 1 over N sum kk Q k Q k sum l e ial left k k right e iamk sum k Q k Q k e iamk sum l p l 2 amp sum k Pi k Pi k end aligned Potansiyel enerji soyle gosterilebilir 12mw2 j xj xj 1 2 12w2 kQkQ k 2 eika e ika 12 kwk2QkQ k displaystyle 1 over 2 m omega 2 sum j x j x j 1 2 1 over 2 omega 2 sum k Q k Q k 2 e ika e ika 1 over 2 sum k omega k 2 Q k Q k wk 2w2 1 cos ka displaystyle omega k sqrt 2 omega 2 1 cos ka Hamilton islevi dalgayoneyli olarak soyle yazilabilir H 12m k PkP k m2wk2QkQ k displaystyle mathbf H 1 over 2m sum k left Pi k Pi k m 2 omega k 2 Q k Q k right Konum degerleri arasindaki baglanti dikkate alinacak bir donusume ugramistir Eger Qlar ve Pler hermitian degiller olsalar donusmus Hamilton islevi N eslememis harmonik saliniciya esit olur Kolaylik icin sinir durumunu periyoduk olarak belirleriz atomun N 1 Esitligi ilk atoma esittir Fiziksel olarak bu zincirin sonuna eklenir Sonuc veren nicelik k kn 2npNafor n 0 1 2 N2 displaystyle k k n 2n pi over Na quad hbox for n 0 pm 1 pm 2 pm N over 2 Ust duzey bag n en az minimum dalga boyundan gelir yukarida tartisildigi gibi kafes boslugu a nin ik katidir Harmonik salinicinin oz degeri ya da wk displaystyle omega k icin enerji duzeyi En 12 n ℏwkn 0 1 2 3 displaystyle E n left 1 over 2 n right hbar omega k quad quad quad n 0 1 2 3 dd Eger sifir noktasi enerjisini yoksayarsak duzeyler soyle siralanir ħw 2ħw 3ħw ħw 2ħw 3ħw dd ħw ħw nin gercek enerji degeri sonraki enerji duzeyinin harmonik salinici kafesine tedarik edilmelidir Elektromanyetik alan sayisal olarak belirlendiginde foton durumunun kiyasinda titresim enerjisinin nicemine fonon denir Tum nicem sistemleri dalgamsi ya da parcacigimsi ozellik gosterirler Fononun parcacigimsi ozellikleri ikinci nicelemede en iyi anlasilir ve islemci teknikleri sonra tanimlanir UygulamalariCift atomlu molekulun titresimi iki cisimli nicem harmonik salinicina ornektir Acisal tekrarsikligi soyle bulunur w km displaystyle omega sqrt frac k mu m displaystyle mu indirgenmis kutledir ve m1m2 m1 m olarak iki atomun kutlesi ile iliskilidir Hooke un atomu basit bir helyum atom modelidir nicem harmonik salinicinda da kullanilir Ustte tartisilan model fononlar Kutle ve yukun degismeyen manyetik alanda olmasi acisal momentumlu tek boyutlu nicem harmonik salinicina ya da iki boyutlu nicem harmonik salinicina bir ornektir KaynakcaIngilizce vikipedi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans




























































