Zaman serisi, istatistik, sinyal işleme, ekonometri ve veri noktalarının sıklığını ifade eder ve düzenli zaman aralıklarında, ardışık zaman alanlarında tipik olarak ölçülür. Zaman serisine örnek olarak, İMKB endeksinin günlük kapanış değeri veya Türkiye'deki Kızılırmak nehrinin yıllık akış hacmi (debisi) verilebilir. Zaman serisi analizi, anlamlı istatistikleri ve verinin diğer istatistiklerini almak için birkaç yöntemi vardır. Zaman serisi tahmini önceden bilinen olayları baz alarak gelecek olayları tahmin etmenin kavramsal modelidir. Ekonometride zaman serisi tahminine bir örnek, önceki başarımlarına (performanslarına) bakarak bir hisse senedinin açılış fiyatını öngörmektir.

Zaman serisi analizinin yöntemleri iki sınıfa ayrılabilir: frekans domeni (frekans uzayı) ve yöntemleri. Önceden tayf analizini (spektrum analizi) içerirken son zamanlarda analizini de kapsar.
Analiz
Farklı amaçlara uygun olan zaman serisinde kullanılabilen veri analizinin birkaç türü vardır.
Genel araştırma
- Veri serisinin grafiksel araştırması.
- Seri bağımlılığı incelemek için otokorelasyon analizi.
- ilişkili olması gerekmeyen döngüsel davranışı incelemek için . Örneğin, güneş yerinin 11 yıllık döngüsel değişkenleri. Diğer yaygın kullanılan örnekler: gökyüzü ile ilgili olaylar, hava durumları, sinirsel hareket, mal fiyatları ve ekonomik hareketler.
Açıklama
- Bileşenlerdeki farklılık, yönelimi, mevsimselliği, yavaş ve hızlı değişimi, döngüsel düzensizliği ifade eder.
- temel özellikleri.
Modeller
Zaman serisi verisinin modelleri birçok biçimde olabilir ve farklı stokastik işlemleri temsil eder. Bir işlem seviyesinde model değişimleri, elverişli önemin üç genel sınıfları özbağlanımlı modeller (AR), tümleşik (I) modeller ve ortalama hareket (MA) modelleridir. Bu üç model önceki veri noktalarında lineerliğe bağlıdır.
Formül
Zaman seri analizinde kullanılan formüllerden biri şudur:
- X = {X1, X2, ...}
Bu, zaman serisini ifade eden temel formüldür. Burada X doğal sayılar dizinidir. Diğer yaygın kullanılan formül de şudur:
- Y = {Yt: t ∈ T}.
Modeller
Özbağlanımlı modelin genel ifadesi AR(p) olarak bilinen şudur:
Burada εt terimi rastgelelik kaynağıdır ve olarak adlandırılır. Aşağıdaki karakteristikleri gösterdiği varsayılır:
1. 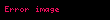
2. 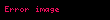
3. 
Bu varsayımlar ile işlem, ikinci dereceden fazla zamanla belirtilir ve katsayıdaki şart koşulu, ikinci derece sabiti olur.
Eğer gürültü normal dağılıma sahipse, normal beyaz gürültü olarak adlandırılır (burada Normal-WN olarak gösterilir):
Bundan dolayı AR işlemi, katsayıdaki şart koşuluna karşı tamamen sabit olabilir.
Ayrıca bakınız
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Zaman serisi istatistik sinyal isleme ekonometri ve veri noktalarinin sikligini ifade eder ve duzenli zaman araliklarinda ardisik zaman alanlarinda tipik olarak olculur Zaman serisine ornek olarak IMKB endeksinin gunluk kapanis degeri veya Turkiye deki Kizilirmak nehrinin yillik akis hacmi debisi verilebilir Zaman serisi analizi anlamli istatistikleri ve verinin diger istatistiklerini almak icin birkac yontemi vardir Zaman serisi tahmini onceden bilinen olaylari baz alarak gelecek olaylari tahmin etmenin kavramsal modelidir Ekonometride zaman serisi tahminine bir ornek onceki basarimlarina performanslarina bakarak bir hisse senedinin acilis fiyatini ongormektir Zaman serisi en uygun ve farkli duzlestirmelere sahip rastgele veri artis egilimi Zaman serisi analizinin yontemleri iki sinifa ayrilabilir frekans domeni frekans uzayi ve yontemleri Onceden tayf analizini spektrum analizi icerirken son zamanlarda analizini de kapsar AnalizFarkli amaclara uygun olan zaman serisinde kullanilabilen veri analizinin birkac turu vardir Genel arastirma Veri serisinin grafiksel arastirmasi Seri bagimliligi incelemek icin otokorelasyon analizi iliskili olmasi gerekmeyen dongusel davranisi incelemek icin Ornegin gunes yerinin 11 yillik dongusel degiskenleri Diger yaygin kullanilan ornekler gokyuzu ile ilgili olaylar hava durumlari sinirsel hareket mal fiyatlari ve ekonomik hareketler Aciklama Bilesenlerdeki farklilik yonelimi mevsimselligi yavas ve hizli degisimi dongusel duzensizligi ifade eder temel ozellikleri ModellerZaman serisi verisinin modelleri bircok bicimde olabilir ve farkli stokastik islemleri temsil eder Bir islem seviyesinde model degisimleri elverisli onemin uc genel siniflari ozbaglanimli modeller AR tumlesik I modeller ve ortalama hareket MA modelleridir Bu uc model onceki veri noktalarinda lineerlige baglidir Formul Zaman seri analizinde kullanilan formullerden biri sudur X X1 X2 Bu zaman serisini ifade eden temel formuldur Burada X dogal sayilar dizinidir Diger yaygin kullanilan formul de sudur Y Yt t T Modeller Ozbaglanimli modelin genel ifadesi AR p olarak bilinen sudur Yt a0 a1Yt 1 a2Yt 2 apYt p et displaystyle Y t alpha 0 alpha 1 Y t 1 alpha 2 Y t 2 cdots alpha p Y t p varepsilon t Burada et terimi rastgelelik kaynagidir ve olarak adlandirilir Asagidaki karakteristikleri gosterdigi varsayilir 1 E et 0 displaystyle E varepsilon t 0 2 E et2 s2 displaystyle E varepsilon t 2 sigma 2 3 E etes 0 t s displaystyle E varepsilon t varepsilon s 0 quad forall t not s Bu varsayimlar ile islem ikinci dereceden fazla zamanla belirtilir ve katsayidaki sart kosulu ikinci derece sabiti olur Eger gurultu normal dagilima sahipse normal beyaz gurultu olarak adlandirilir burada Normal WN olarak gosterilir et t T Normal WN displaystyle varepsilon t t in T mbox Normal WN Bundan dolayi AR islemi katsayidaki sart kosuluna karsi tamamen sabit olabilir Ayrica bakinizOtokorelasyonKaynakca
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans