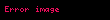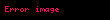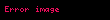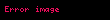Matematiğin bir dalı olan karmaşık analizde, Augustin Louis Cauchy'nin ismine atfedilen Cauchy integral teoremi, karmaşık düzlemdeki holomorf fonksiyonların çizgi integralleri hakkında önemli bir teoremdir. Esasen, teoremin ifade ettiği şudur: İki ayrı yol aynı iki noktayı birbirine bağlıyorsa ve bir fonksiyon bu iki ayrı yolun arasındaki iç bölgede holomorfsa, o zaman fonksiyonun bu iki yol integrali birbirine eşittir.
Teorem, kapalı yollar için ise şu şekilde ifade edilir. U, C 'nin basit bağlantılı açık bir altkümesi olsun. f : U → C holomorf bir fonksiyon olsun ve γ, U içinde başlangıç noktası bitiş noktasıyla aynı olan bir yol olsun. O zaman
eşitliği vardır.
tarafından gösterildiği gibi, Cauch integral teoremi, U içinde her yerde f 'nin karmaşık türevi olan f '(z) varsa, kanıtlanabilir. Bu önemlidir çünkü bu fonksiyonlar için o zaman Cauchy integral formülü de kanıtlanabilir ve bundan aslında bu fonksiyonların özelliği çıkar.
U 'nun basit bağlantılı olması koşulu U 'da "delik" olmaması anlamına gelir veya homotopi kavramlarıyla tartışılacak olursa, U 'nun temel grubunun bariz olması demektir. Örneğin, açık diski bunlardan biridir. Bu şart teoremde çok önemlidir. Birim çemberi dolaşan
düşünüldüğünde,
yol integrali sıfır olmayacaktır. Cauchy integral teoremi, f(z) = 1/z fonksiyonu z = 0 noktasında tanımlı olmadığı (ve tabi holomorf olmadığı) için artık burada geçerli değildir.
Teoremin önemli sonuçlarından birisi basit bağlantılı bölgelerdeki holomorf fonksiyonların yol integrallerinin hesabın temel teoremindekine benzer bir şekilde hesaplanabilmesidir: U, C 'nin basit bağlantılı açık bir kümesi olsun. f : U → C holomorf bir fonksiyon olsun ve γ, başlangıç noktası a, bitiş noktası b olan bir olsun. F, f 'nin ise, o zaman
eşitliği vardır.
Cauchy integral teoremi üstte verilen halinden biraz daha güçlü halde de geçerlidir. U 'nun sınırı doğrultulabilir bir yolun (mesela γ) görüntüsü olsun ve ayrıca U basit bağlantılı açık bir C altkümesi olsun. f, U üzerinde holomorf olan bir fonksiyonsa ve U 'nun kapanışında sürekliyse, o zaman
eşitliği vardır.
Cauchy integral teoremi ayrıca Cauchy integral formülü 'nün ve rezidü (kalıntı) teoreminin kanıtlanmasını da sağlar.
KANIT
Cauchy integral teoremi Vektör Analizi'nde ki Green Teoremi ile kanıtlanabilir. Sebebi karmaşık değerli fonksiyonların vektörel fonksiyon gibi davranmasıdır. Kanıt için Cauchy-Riemann denklemlerini kullanmamız gerekir. kontürü saat yönünün tersi şeklinde bir döngü halinde olsun ve U kümesi basit bağlantılı ve kümesinin alt kümesi olsun. fonksiyonu U gibi bir basit bağlantılı fonksiyonun tümüne holomorf olsun.
ve fonksiyonun değişkeninin diferansiyeli dir.
Bu durumda
olacaktır.
Green Teoremine dayanarak
Cauchy-Riemann denklemleriyle teorem kanıtlanacaktır.
ve
= 0
Ve sonunda
Ayrıca bakınız
Dış bağlantılar
- http://mathworld.wolfram.com/CauchyIntegralTheorem.html 12 Temmuz 2008 tarihinde Wayback Machine sitesinde . MathWorld'deki ilgili sayfa.
- Cauchy-Goursat Teoremi Modülü, John H. Mathews tarafından 15 Temmuz 2008 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir dali olan karmasik analizde Augustin Louis Cauchy nin ismine atfedilen Cauchy integral teoremi karmasik duzlemdeki holomorf fonksiyonlarin cizgi integralleri hakkinda onemli bir teoremdir Esasen teoremin ifade ettigi sudur Iki ayri yol ayni iki noktayi birbirine bagliyorsa ve bir fonksiyon bu iki ayri yolun arasindaki ic bolgede holomorfsa o zaman fonksiyonun bu iki yol integrali birbirine esittir Teorem kapali yollar icin ise su sekilde ifade edilir U C nin basit baglantili acik bir altkumesi olsun f U C holomorf bir fonksiyon olsun ve g U icinde baslangic noktasi bitis noktasiyla ayni olan bir yol olsun O zaman gf z dz 0 displaystyle oint gamma f z dz 0 esitligi vardir tarafindan gosterildigi gibi Cauch integral teoremi U icinde her yerde f nin karmasik turevi olan f z varsa kanitlanabilir Bu onemlidir cunku bu fonksiyonlar icin o zaman Cauchy integral formulu de kanitlanabilir ve bundan aslinda bu fonksiyonlarin ozelligi cikar U nun basit baglantili olmasi kosulu U da delik olmamasi anlamina gelir veya homotopi kavramlariyla tartisilacak olursa U nun temel grubunun bariz olmasi demektir Ornegin U z z z0 lt r displaystyle U z z z 0 lt r acik diski bunlardan biridir Bu sart teoremde cok onemlidir Birim cemberi dolasan g t eitt 0 2p displaystyle gamma t e it quad t in left 0 2 pi right dusunuldugunde g1zdz 02pieiteitdt 02pidt 2pi displaystyle oint gamma frac 1 z dz int 0 2 pi ie it over e it dt int 0 2 pi i dt 2 pi i yol integrali sifir olmayacaktir Cauchy integral teoremi f z 1 z fonksiyonu z 0 noktasinda tanimli olmadigi ve tabi holomorf olmadigi icin artik burada gecerli degildir Teoremin onemli sonuclarindan birisi basit baglantili bolgelerdeki holomorf fonksiyonlarin yol integrallerinin hesabin temel teoremindekine benzer bir sekilde hesaplanabilmesidir U C nin basit baglantili acik bir kumesi olsun f U C holomorf bir fonksiyon olsun ve g baslangic noktasi a bitis noktasi b olan bir olsun F f nin ise o zaman gf z dz F b F a displaystyle int gamma f z dz F b F a esitligi vardir Cauchy integral teoremi ustte verilen halinden biraz daha guclu halde de gecerlidir U nun siniri dogrultulabilir bir yolun mesela g goruntusu olsun ve ayrica U basit baglantili acik bir C altkumesi olsun f U uzerinde holomorf olan bir fonksiyonsa ve U nun kapanisinda surekliyse o zaman gf z dz 0 displaystyle oint gamma f z dz 0 esitligi vardir Cauchy integral teoremi ayrica Cauchy integral formulu nun ve rezidu kalinti teoreminin kanitlanmasini da saglar KANIT Cauchy integral teoremi Vektor Analizi nde ki Green Teoremi ile kanitlanabilir Sebebi karmasik degerli fonksiyonlarin vektorel fonksiyon gibi davranmasidir Kanit icin Cauchy Riemann denklemlerini kullanmamiz gerekir g displaystyle gamma konturu saat yonunun tersi seklinde bir dongu halinde olsun ve U kumesi basit baglantili ve C displaystyle mathbb C kumesinin alt kumesi olsun f z displaystyle f z fonksiyonu U gibi bir basit baglantili fonksiyonun tumune holomorf olsun f z u x y i v x y displaystyle f z u x y i v x y ve fonksiyonun degiskeninin diferansiyeli dz dx i dy displaystyle dz dx i dy dir Bu durumda gf z dz displaystyle oint gamma f z dz g u iv dx idy g u dx v dy i g v dx u dy displaystyle oint gamma u iv dx idy oint gamma u dx v dy i oint gamma v dx u dy olacaktir Green Teoremine dayanarak g u dx v dy D v x u y dx dy displaystyle oint gamma u dx v dy iint limits D partial v over partial x partial u over partial y dx dy g v dx u dy D u x v y dx dy displaystyle oint gamma v dx u dy iint limits D partial u over partial x partial v over partial y dx dy Cauchy Riemann denklemleriyle teorem kanitlanacaktir u x v y displaystyle partial u over partial x partial v over partial y ve v x u y displaystyle partial v over partial x partial u over partial y D v x u y dx dy displaystyle iint limits D partial v over partial x partial u over partial y dx dy D u y u y dx dy 0 displaystyle iint limits D partial u over partial y partial u over partial y dx dy 0 D u x v y dx dy displaystyle iint limits D partial u over partial x partial v over partial y dx dy D u x u x dx dy displaystyle iint limits D partial u over partial x partial u over partial x dx dy 0 Ve sonunda gf z dz 0 displaystyle oint gamma f z dz 0 Ayrica bakinizCauchy Riemann denklemleri Cauchy integral formulu Morera teoremi Kalinti karmasik analiz Dis baglantilarhttp mathworld wolfram com CauchyIntegralTheorem html 12 Temmuz 2008 tarihinde Wayback Machine sitesinde MathWorld deki ilgili sayfa Cauchy Goursat Teoremi Modulu John H Mathews tarafindan 15 Temmuz 2008 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State


![{\displaystyle \gamma (t)=e^{it}\quad t\in \left[0,2\pi \right]}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4eU1UVXpORFUwWWpkbE5EQTFNRGhpWXpnMVlqTm1aalExTldFNFl6ZGhOak16TnpWbVlXSTQuc3Zn.svg)