Diofantos

Diofantos (Grekçe: Διόφαντος ὁ Ἀλεξανδρεύς, romanize: Diofantos ho Aleksandreus; y. MS 200 ile 214 arasında doğdu; 84 yaş civarında, muhtemelen MS 284 ile 298 arasında öldü.) cebirin babası olarak tanımlanan, cebir denklemleri ve sayılar teorisi üzerine Arithmetika adlı eserin yazarı olan Yunan matematikçi.Değişkenleri sadece tam sayılar olan ve kendi adını taşıyan Diofantos denklemiyle de bilinir.

Diofantos
Doğum	MS 200-214
Ölüm	MS 284-298
Milliyet	Yunan
Kariyeri
Dalı	Matematik

İskenderiyeli bir matematikçiydi ve çoğu artık kaybolmuş olan Arithmetica adı verilen bir kitap dizisinin yazarı idi. Metinleri cebirsel denklemleri çözmekle ilgilidir. Claude Gaspard Bachet de Méziriac'ın Diofantos'un Arithmetica baskısını okurken Pierre de Fermat, Diofantos tarafından ele alınan belirli bir denklemin çözümü olmadığı sonucuna vardı ve ayrıntıya girmeden kenar boşluğunda "bu önermenin gerçekten harika bir kanıtını" bulduğunu kaydetti. Bu anekdot, Fermat'nın Son Teoremi olarak anılır ve sayı teorisinde muazzam ilerlemelere yol açarak Diofantos denklemlerinin ("Diofantos geometrisi") ve Diofantos yaklaşımlarının incelenmesi, matematiksel araştırmanın önemli alanları olmaya devam ediyor. Diofantos, yaklaşık bir eşitliği ifade etmek için παρισότης (parisotes) terimini icat etti. Bu terim Latincede adaequalitas olarak çevrildi ve Pierre de Fermat tarafından fonksiyonlar için maksimumlar ve eğrilere teğet doğrular bulmak için geliştirilen yeterlilik tekniği haline geldi. Diofantos, kesirleri sayı olarak tanıyan ilk Yunan matematikçiydi; böylece katsayılar ve çözümler için pozitif rasyonel sayılara izin verdi. Modern kullanımda, Diofantos denklemleri genellikle tam sayı çözümleri aranan tam sayı katsayılı cebirsel denklemlerdir.

Yaşamı

Diofantos'un hayatı hakkında maalesef oldukça az bilgi mevcuttur. Hangi dönemde yaşadığıyla ilgili yapılan çıkarımlar ancak 500 yıllık bir döneme indirgenebilmiştir. Kendisinin Poligon sayılarla ilgili çalışmasında, MÖ 2. yüzyılda yaşamış olan İskenderiyeli Hipsikles'ten bahsetmiş olmasının yanı sıra, MS 4. yüzyılda yaşamış olan İskenderiyeli Theon'un da Diofantos'tan alıntı yapmış olması, Diofantos'un MÖ 2. yüzyılla MS 4. yüzyıl arasında bir dönemde yaşamış olduğunu düşündürmüştür. Diofantos'un kaç yaşında öldüğüyle ilgili bilgiye ise, MS 5. yüzyılda yaşamış olan Metodorus'un, çeşitli matematik bilmecelerini derlediği, Yunan Antolojisi adlı eserinden ulaşıyoruz. Bu eserde Diofantos'un öldüğü yaş ile ilgili bilmece şöyledir:

• Diofantos hayatının 1/6'nda ergenliğe erişmiştir.
• Hayatının 1/12'sini tamamladığında sakal bırakmaya başlamıştır.
• Hayatının 1/7'sini tamamladığında evlenmiştir.
• 5 yıl sonra bir oğlu olmuştur.
• Oğlu, Diofantos'un hayatının yarısı kadar yaşamıştır.
• Oğlunun ölümünden 4 yıl sonra da Diofantos ölmüştür.

Eğer D Diofantos'un öldüğü yaşı belirtirse, bu bilmecenden aşağıdaki denklem türetilir:

${\displaystyle D=(1/6+1/7+1/12)D+5+(1/2)D+4}$.

Bu denklemin çözümü de Diofantos'un 84 yaşında öldüğü sonucunu verir.

Bilimsel katkıları

Diofantos her ne kadar cebirin yaratıcısı olarak tanımlansa da Diofantos'un yaşadığı dönemdeki Yunan Matematikçiler, Antik Mısır cebirinden haberdardılar. Tek bilinmeyenli cebir problemleri ve çözümleri MÖ 1650 yılında yazılmış olan Rhind Papirüsü'nde de geçmektedir. Dolayısıyla Diofantos'un en önemli katkısı, kendisinden önce gelen matematikçilerin çalışmalarını bir arada toplayıp, bunların uygulama alanlarını genişletmesidir. Ayrıca bir diğer katkısı da matematiksel gösterimleri sadece semboller yardımıyla yapmış olmasıdır.

Arithmetika

1621 yılında basılan Arithmetica'nın kapağı, Yunancadan Latinceye çeviri

Arithmetika, Diofantos'un 13 cilten oluşan ve sadece 6 cildinin günümüze ulaşabildiği, yazarın opus magnum’udur. 19. yüzyılda yaşamış olan Matematik tarihçisi 'in tanımlamasına göre, "Arithmetika 5 farklı kategoride 130 problemi içerir." Hankel ayrıca bu problemleri çözümlenişlerine göre iki gruba ayırır:

1) Tek çözümü olanlar (Determinate)

2) Genel çözümü olanlar (Indeterminate).

1. cilt tek çözümlü cebir problemlerini içerirken, 2, 3, 4 ve 5. ciltler genel çözümlü cebir problemlerini içerir. 6. cilt ise dik üçgenle ilgili aritmetik problemleri içerir. Diofantos Arithmetika'daki problemleri analitik bir şekilde, değişkenleri ve bilinmeyenleri semboller yardımıyla ifade etmiştir.

Diofantos'un ölümünden sonra Arithmetika ve diğer çalışmaları batı dünyasında (Avrupa'nın Karanlık Çağ'a girmesinden dolayı) unutulmuştur. Arithmetika'nın büyük bölümünün bugüne ulaşabilmesinin sebebi, Arap alimlerin bu eser üzerinde tafsilatlı bir şekilde çalışmasıdır.

Arithmetika'nın Latinceye ilk çevirisi tarafından 1570 yılında yapılmış fakat basılmamıştır. Bununla birlikte Bombelli, Diophontos'un çalışmasının bir kısmını kendi cebir çalışmasında kullanmıştır. Arithmetika'nın en bilinen Latince çevirisi ise tarafından 1621 yılında yapılmıştır. Arithmetika'nın 1621 baskısı, Fermat'ın meşhur Son Teorem'ini yazmasından sonra daha da bir önem kazanmıştır.

Diofantos denklemi

Diofantos denklemi, çözümü tam sayı olan ve içindeki tüm değişkenlerin de tam sayı olduğu denklemlerdir. Diofantos bu denklemlerde çıkarma işlemi, bilinmeyen değişkenler ve sayının üs değişkenleri için semboller kullanmıştır. Bu denklemlere en basit örnek (modern sembollerle) aşağıdaki gibidir;

${\displaystyle aX=b}$

- a ve b tam katsayılar, X ise bir tam sayı bilinmeyendir.

İki değişkenli örnek:

${\displaystyle X+Y=1}$

Bu eşitlikte her bir X değeri için tek bir Y çözümü vardır (${\displaystyle Y=1-X}$). Bu eşitliğin çözüm kümesi ise şudur:

Her X ∈ Z için (X, 1 − X)

Diğer çalışmaları

Diofantos, Arithmetica dışında başka birkaç kitap daha yazdı, ancak çok azı hayatta kaldı. Diophontus'un diğer bilinen çalışmaları, Porizmler (Yunanca: Porismata) isimli bir eser ve çokgensel sayılar üzerine yazılmış olan başka bir eserdir. Çokgensel sayılar üzerine olan çalışmalarının bazı fragmanları bugüne ulaşmıştır fakat Porizmler isimli eseri tamamen kaybolmuştur.

Porizmler

Diofantos'un kendisi, The Porisms (veya Porismata) adlı lemmalardan oluşan bir esere atıfta bulunur, ancak bu kitap tamamen kaybolmuştur.

Porizmler adlı eser kaybolsa da, Diofantos Arithmetica’da bunlardan bahsettiği için orada bulunan üç lemmanın olduğunu biliyoruz. Bir lemma, iki rasyonel sayının küplerinin farkının diğer iki rasyonel sayının küplerinin toplamına eşit olduğunu belirtir, yani 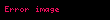${\displaystyle a>b}$ olmak üzere herhangi bir ${\displaystyle a}$ ve ${\displaystyle b}$ verildiğinde, hepsi pozitif ve rasyonel olan öyle ${\displaystyle c}$ ve ${\displaystyle d}$ vardır ki aşağıdaki eşitliği sağlar:

a³ − b³ = c³ + d³.

Çokgensel sayılar ve geometrik ögeler

Diofantos'un Pisagor ve Pisagorcular için büyük ilgi gören bir konu olan çokgensel (poligonal) sayılar üzerine de yazdığı bilinmektedir. ilgili bir kitabının parçaları mevcuttur.

Preliminaries to the Geometric Elements adlı bir kitap, geleneksel olarak İskenderiyeli Heron'a atfedilmiştir. Son zamanlarda, Heron'a atıfta bulunmanın yanlış olduğunu ve gerçek yazarın Diofantos olduğunu öne süren Wilbur Knorr tarafından incelenmiştir.

Etkileri

Diofantos'un çalışmaları tarihte büyük bir etkiye sahipti. Arithmetica’nın baskıları on altıncı yüzyılın sonlarında ve 17. ve 18. yüzyıllarda Avrupa'da cebirin gelişimi üzerinde derin bir etki yaptı. Diofantos ve eserleri de Arap matematiğini etkiledi ve Arap matematikçiler arasında büyük ün kazandı. Diofantos'un çalışması cebir üzerine çalışmak için bir temel oluşturdu ve aslında ileri matematiğin çoğu cebire dayanmaktadır. Hindistan'ı ne kadar etkilediği tartışma konusudur.

Diofantos genellikle "cebirin babası" olarak adlandırılır çünkü sayı teorisine, matematiksel gösterime büyük katkıda bulunmuştur ve Arithmetica senkoplu gösterimin bilinen en eski kullanımını içermektedir.

Diofantos analizi

Günümüzde, Diofantos analizi, denklemler için tam sayı çözümlerinin arandığı çalışma alanıdır ve Diofantos denklemleri, yalnızca tam sayı çözümlerinin arandığı tam sayı katsayılı polinom denklemleridir. Belirli bir Diofantos denkleminin çözülebilir olup olmadığını söylemek genellikle oldukça zordur. Arithmetica’daki problemlerin çoğu ikinci dereceden denklemlere dönüşür. Diofantos, 3 farklı ikinci dereceden denklem tipini ele aldı: ax² + bx = c, ax² = bx + c, and ax² + c = bx. İkinci dereceden denklemlerle ilgili bugün tek bir durum varken Diofantos'un üç durumu (yukarıdaki üç durum) olmasının nedeni, sıfır fikrine sahip olmaması ve verilen ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$ sayılarının her birinde pozitif olduğunu düşünerek negatif katsayılardan kaçınmasıdır. Diofantos her zaman rasyonel bir çözümden memnundu ve tam sayıya ihtiyaç duymuyordu, bu da kesirleri problemlerine çözüm olarak kabul ettiği anlamına geliyordu. Diofantos, negatif veya irrasyonel karekök çözümlerini "yararsız", "anlamsız" ve hatta "saçma" olarak değerlendirdi. Spesifik bir örnek vermek gerekirse, 4 = 4x + 20 denklemini 'absurd' olarak adlandırır çünkü bu x için negatif bir çözüm değerine yol açar. İkinci dereceden bir denklemde aradığı tek sonuç bir çözümdü. Diofantos'un ikinci dereceden bir denklemin iki çözümü olabileceğini bile fark ettiğini gösteren hiçbir kanıt yoktur. Eşzamanlı ikinci dereceden denklemleri de düşünmüştür.

Matematiksel gösterim

Diofantos, matematiksel gösterimde önemli ilerlemeler kaydetti ve cebirsel gösterimi ve sembolizmi kullandığı bilinen ilk kişi oldu. Ondan önce herkes denklemleri tamamen yazdı. Diofantos, sık sık meydana gelen işlemler için kısaltılmış bir gösterim ve bilinmeyen ile bilinmeyenin kuvvetleri için bir kısaltma kullanan cebirsel bir sembolizm getirdi. Matematik tarihçisi şöyle der:

“	"Diofantos'un ilk kez ortaya koyduğu ve şüphesiz kendi tasarladığı sembolizm, bir denklemi ifade etmek için kısa ve kolayca anlaşılır bir yol sağladı ..." Eşittir "kelimesi için de bir kısaltma kullanıldığından, Diofantos, sözel cebirden sembolik cebire doğru temel bir adım attı.	„

Diofantos, sembolizmde önemli ilerlemeler kaydetmiş olsa da, daha genel yöntemleri ifade etmek için hala gerekli gösterime sahip değildi. Bu, çalışmalarının genel durumlardan çok belirli sorunlarla ilgilenmesine neden oldu. Diofantos notasyonunun bazı sınırlamaları, yalnızca bir bilinmeyen için notasyonunun olması ve problemler birden fazla bilinmeyeni içerdiğinde, Diofantos'un kelimelerle "ilk bilinmeyen", "ikinci bilinmeyen" vb. ifadelere indirgenmesidir. Ayrıca genel bir n sayısı için bir sembolü yoktu. Biz 12 + 6n/n² − 3 yazdığımızda, Diofantos, "... on iki artırılmış altı kat sayı, sayının karesinin üçe geçtiği farka bölünür" gibi yapılara başvurmak zorundadır.

Çok genel problemlerin yazılabilmesi, kısa ve öz bir şekilde çözülebilmesi için cebirin hâlâ kat etmesi gereken çok yol vardı.

Kaynakça

Özel

1. ^ ^{a b} . Ansiklopedi Maddesi. 12 Eylül 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Ekim 2012. 
2. ^ ^{a b c} O'Connor, John J.; Robertson, Edmund F., "Diofantos", MacTutor Matematik Tarihi arşivi 
3. ^ Eric W. Weisstein, Diophantine Equation (MathWorld)
4. ^ ; Schaps, David; (2013), "Almost Equal: The Method of Adequality from Diophantus to Fermat and Beyond", , 21 (3), ss. 283-324, arXiv:1210.7750 $2, Bibcode:2012arXiv1210.7750K, doi:10.1162/POSC_a_00101 
5. ^ Bashmakova, Isabella G. (1998). . Cambridge University Press. ss. 81-84. 2 Şubat 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Ekim 2012. 
6. ^ Darling, David (2004). . John Wiley & Sons. s. 94. 10 Mart 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Ekim 2012. 
7. ^ Kostadinov, Kalin. (PDF). Boston University. 15 Mayıs 2014 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 28 Ekim 2012. 
8. ^ Kirschenbaum, Marni. "Alexandrian Algebra according to Diophantus". Ruthgers. 21 Mart 2015 tarihinde kaynağından . Erişim tarihi: 28 Ekim 2012. 
9. ^ ^{a b} "Diophantus". 21 Ekim 2013 tarihinde kaynağından . Erişim tarihi: 28 Ekim 2012. 
10. ^ "Diophantus". 15 Mayıs 2015 tarihinde kaynağından . Erişim tarihi: 29 Ekim 2012. 
11. ^ Knorr, Wilbur: Arithmêtike stoicheiôsis: On Diophantus and Hero of Alexandria, in: Historia Matematica, New York, 1993, Vol.20, No.2, ss. 180-192
12. ^ Carl B. Boyer, A History of Mathematics, 2. bas. (Wiley, 1991), s. 228
13. ^ Kurt Vogel (2008), "Diophantus of Alexandria", Complete Dictionary of Scientific Biography, Encyclopedia.com 

Genel

• Allard, A. "Les scolies aux arithmétiques de Diophante d'Alexandrie dans le Matritensis Bibl.Nat.4678 et les Vatican Gr.191 et 304" Byzantion 53. Brussels, 1983: 682-710.
• Bachet de Méziriac, C.G. Diophanti Alexandrini Arithmeticorum libri sex et De numeris multangulis liber unus. Paris: Lutetiae, 1621.
• Bashmakova, Izabella G. Diophantos. Arithmetica and the Book of Polygonal Numbers. Introduction and Commentary Translation by I.N. Veselovsky. Moscow: Nauka [in Russian].
• Christianidis, J. "Maxime Planude sur le sens du terme diophantien "plasmatikon"", Historia Scientiarum, 6 (1996) 37-41.
• Christianidis, J. "Une interpretation byzantine de Diophante", Historia Mathematica, 25 (1998) 22-28.
• Czwalina, Arthur. Arithmetik des Diophantos von Alexandria. Göttingen, 1952.
• Heath, Sir Thomas, Diophantos of Alexandria: A Study in the History of Greek Algebra, Cambridge: Cambridge University Press, 1885, 1910.
• Robinson, D. C. and Luke Hodgkin. History of Mathematics, King's College London, 2003.
• Rashed, Roshdi. L’Art de l’Algèbre de Diophante. éd. arabe. Le Caire: Bibliothèque Nationale, 1975.
• Rashed, Roshdi. Diophante. Les Arithmétiques. Volume III: Book IV; Volume IV: Books V–VII, app., index. Collection des Universités de France. Paris (Société d’Édition “Les Belles Lettres”), 1984.
• Sesiano, Jacques. The Arabic text of Books IV to VII of Diophantus’ translation and commentary. Thesis. Providence: Brown University, 1975.
• Sesiano, Jacques. Books IV to VII of Diophantus’ Arithmetica in the Arabic translation attributed to Qusṭā ibn Lūqā, Heidelberg: Springer-Verlag, 1982. , DOI:10.1007/978-1-4613-8174-7.
• Σταμάτης, Ευάγγελος Σ. Διοφάντου Αριθμητικά. Η άλγεβρα των αρχαίων Ελλήνων. Αρχαίον κείμενον – μετάφρασις – επεξηγήσεις. Αθήναι, Οργανισμός Εκδόσεως Διδακτικών Βιβλίων, 1963.
• Tannery, P. L. Diophanti Alexandrini Opera omnia: cum Graecis commentariis, Lipsiae: In aedibus B.G. Teubneri, 1893-1895 (çevrimiçi: Cilt. 1, Cilt. 2)
• Ver Eecke, P. Diophante d’Alexandrie: Les Six Livres Arithmétiques et le Livre des Nombres Polygones, Bruges: Desclée, De Brouwer, 1921.
• Wertheim, G. Die Arithmetik und die Schrift über Polygonalzahlen des Diophantus von Alexandria. Übersetzt und mit Anmerkungen von G. Wertheim. Leipzig, 1890.

Konuyla ilgili yayınlar

• Bashmakova, Izabella G. "Diophante et Fermat," Revue d'Histoire des Sciences 19 (1966), ss. 289-306 (Fransızca).
• Bashmakova, Izabella G. . Moscow: Nauka 1972 (Rusça).
  • Almanca çeviri: Diophant und diophantische Gleichungen. Birkhauser, Basel/ Stuttgart, 1974.
  • İngilizce çeviri: Diophantus and Diophantine Equations. Hardy Grant'in editöryel yardımlarıyla Abe Shenitzer tarafından çevrilmiş ve Joseph Silverman tarafından güncellenmiştir. The Dolciani Mathematical Expositions, 20. Mathematical Association of America, Washington, DC. 1997.
• Bashmakova, Izabella G. “Arithmetic of Algebraic Curves from Diophantus to Poincaré,” Historia Mathematica 8 (1981), 393-416 (İngilizce).
• Bashmakova, Izabella G., Slavutin, E.I. History of Diophantine Analysis from Diophantus to Fermat. Moscow: Nauka 1984 (Rusça).
• Heath, Sir Thomas (1981). A history of Greek mathematics (İngilizce). 2. Cambridge: Cambridge University Press. 
• Rashed, Roshdi, Houzel, Christian. Les Arithmétiques de Diophante : Lecture historique et mathématique, Berlin, New York: Walter de Gruyter, 2013 (Fransızca).
• Rashed, Roshdi, Histoire de l’analyse diophantienne classique : D’Abū Kāmil à Fermat, Berlin, New York: Walter de Gruyter. (Fransızca)
• Vogel, Kurt (1970). "Diophantus of Alexandria". Dictionary of Scientific Biography (İngilizce). 4. New York: Scribner. 
• S. Çenberci (2009), Diophantine Denklemi (PDF), erişim tarihi: 18 Şubat 2021 
• Caner Ağaoğlu (2015), Bazı Diophantine Denklemleri Çözmek için Elementer Metotlar ve Bunların Uygulamaları (PDF), Uludağ Üniversitesi, erişim tarihi: 18 Şubat 2021 
• Mehmet Kılıç (2016), Bazı Diophantine Denklemlerin Çözümleri Üzerine (PDF), erişim tarihi: 18 Şubat 2021 

Dış bağlantılar

Vikisöz'de Diofantos ile ilgili sözleri bulabilirsiniz.

• Wikimedia Commons'ta Diophantus ile ilgili çoklu ortam belgeleri bulunur
•  Bu madde artık kamu malı olan bir yayından alınan metni içeriyor: Chisholm, Hugh, (Ed.) (1911). "madde adı gerekli". Encyclopædia Britannica (11. bas.). Cambridge University Press. 
• (İngilizce). 21 Ekim 2013 tarihinde kaynağından arşivlendi. Diophantus hakkında genel bilgi 
• (PDF). 11 Aralık 2013 tarihinde kaynağından (PDF) arşivlendi. 
• Eric W. Weisstein, Diophantus Bilmecesi (İngilizce) (MathWorld)
• Norbert Schappacher (2005), Diophantus of Alexandria : a Text and its History (PDF), 6 Ocak 2021 tarihinde kaynağından (PDF), erişim tarihi: 18 Şubat 2021 
• Jan P. Hogendijk, Review of Sesiano's Diophantus, 14 Temmuz 2014 tarihinde kaynağından , erişim tarihi: 18 Şubat 2021, Review of J. Sesiano, Books IV to VII of Diophantus' Arithmetica 
• , Latin translation from 1575, 13 Haziran 2012 tarihinde kaynağından , erişim tarihi: 19 Mart 2022