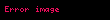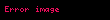Temel cebirde eşitsizlik, iki değer arasındaki farkı ifade eden bir ilişkidir ve gibi sembollerle gösterilir.
- a ≠ b gösterimi; "a eşit değildir b". Birinin diğerinden daha büyük veya küçük olduğunu yani iki elemanın birbirine eşit olmadığını ifade eder.

Ögeleri (elemanları) tam sayı veya reel sayılardan oluşan bir denklemin değerleri büyüklüklerine göre karşılaştırılır.
- a < b gösterimi; "a küçüktür b" anlamına gelir.
- a > b gösterimi; "a büyüktür b" anlamına gelir.
Her iki durumda da "a, b ye eşit değildir".
Tamamen eşitsiz olmayan iki tür vardır.
- a ≤ b gösterimi; "a, küçük eşittir b".
- a ≥ b gösterimi; "a, büyük eşittir b".
Bir eşitsizliğin her iki tarafına aynı sayı eklenir ya da aynı sayı çıkarılırsa eşitsizlik bozulmaz.
Eşitsizlik gibi denklem ve diğer cebirsel ifadelerde de bu kural geçerlidir. İfadenin çözümü için gerekli olan temel prensip de budur. Eşitsizliğin her iki tarafı negatif bir sayı ile çarpılır veya negatif bir sayıya bölünürse eşitsizlik yön değiştirir.
bu bir eşitsizlik örneğidir. Çözümü için her iki taraf ile toplanır böylece:
olur.
Buradan şu sonuç çıkarılır: sayısı ile (eksi sonsuz) arasındadır.
Bu durum şu şekilde gösterilir:
Büyük eşittir, küçük eşittir
Bu sembollerde de büyüktür ve küçüktürdeki gibi işlemler yapılır ancak gösterim şekli ve kapsadığı sayılar biraz farklıdır.
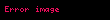
şimdi bu örnekte 

Bu sefer 
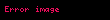
Yani şöyle:


Ortalamalar arasındaki eşitsizlikler
Ortalamalar arasında birçok eşitsizlik vardır. Örneğin; a1, a2, …, an pozitif sayıları için H ≤ G ≤ A ≤ Q olur, şöyle ki:
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Temel cebirde esitsizlik iki deger arasindaki farki ifade eden bir iliskidir ve lt gt displaystyle leq lt geq gt gibi sembollerle gosterilir a b gosterimi a esit degildir b Birinin digerinden daha buyuk veya kucuk oldugunu yani iki elemanin birbirine esit olmadigini ifade eder Ornek bir esitsizlik grafigi Ogeleri elemanlari tam sayi veya reel sayilardan olusan bir denklemin degerleri buyukluklerine gore karsilastirilir a lt b gosterimi a kucuktur b anlamina gelir a gt b gosterimi a buyuktur b anlamina gelir Her iki durumda da a b ye esit degildir Tamamen esitsiz olmayan iki tur vardir a b gosterimi a kucuk esittir b a b gosterimi a buyuk esittir b Bir esitsizligin her iki tarafina ayni sayi eklenir ya da ayni sayi cikarilirsa esitsizlik bozulmaz Esitsizlik gibi denklem ve diger cebirsel ifadelerde de bu kural gecerlidir Ifadenin cozumu icin gerekli olan temel prensip de budur Esitsizligin her iki tarafi negatif bir sayi ile carpilir veya negatif bir sayiya bolunurse esitsizlik yon degistirir x 6 lt 9 displaystyle x 6 lt 9 bu bir esitsizlik ornegidir Cozumu icin her iki taraf 6 displaystyle 6 ile toplanir boylece x lt 3 displaystyle x lt 3 olur Buradan su sonuc cikarilir x displaystyle x sayisi 3 displaystyle 3 ile displaystyle infty eksi sonsuz arasindadir Bu durum su sekilde gosterilir 3 displaystyle infty 3 Buyuk esittir kucuk esittirBu sembollerde de buyuktur ve kucukturdeki gibi islemler yapilir ancak gosterim sekli ve kapsadigi sayilar biraz farklidir x 6 9 displaystyle x 6 leq 9 simdi bu ornekte x displaystyle x i yalniz birakildiginda x 3 displaystyle x leq 3 olur yani sistem ayni ancak gosterimde minik bir farklilik vardir Bu sefer 3 displaystyle 3 de dahil displaystyle infty a giden sayilar vardir Yani soyle 3 displaystyle infty 3 3 displaystyle 3 un yaninda koseli parantez kullanilmasinin sebebi aradaki isaretin displaystyle leq olmasidir Ortalamalar arasindaki esitsizliklerOrtalamalar arasinda bircok esitsizlik vardir Ornegin a1 a2 an pozitif sayilari icin H G A Q olur soyle ki H n1 a1 1 a2 1 an displaystyle H frac n 1 a 1 1 a 2 cdots 1 a n harmonik ortalama G a1 a2 ann displaystyle G sqrt n a 1 cdot a 2 cdots a n geometrik ortalama A a1 a2 ann displaystyle A frac a 1 a 2 cdots a n n aritmetik ortalama Q a12 a22 an2n displaystyle Q sqrt frac a 1 2 a 2 2 cdots a n 2 n karekok ortalama
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans