Diferansiyel Denklemler

Matematikte, diferansiyel denklem, bir ya da birden fazla fonksiyonu ve bunların türevlerini ilişkilendiren denklemdir.Fizik, kimya, mühendislik, biyoloji ve ekonomi alanlarında matematiksel modeller genellikle diferansiyel denklemler kullanılarak ifade edilirler. Bu denklemlerde, fonksiyonlar genellikle fiziksel ya da finansal değerlere, fonksiyon türevleriyse değerlerin değişim hızlarına denk gelir.

Çeşitleri

Diferansiyel denklemler temel olarak iki kola ayrılırlar:

1. Normal diferansiyel denklemler (veya adi diferansiyel denklemler)
2. Kısmi diferansiyel denklemler .

Diferansiyel denklemler bilinmeyenlerin birbirleri ve katsayılarla ilgili konumlarına göre: , Doğrusal olmayan diferansiyel denklemler olarak da gruplanmaktadır. Doğrusal denklemlerin teorisi gelişmiş olmasına rağmen doğrusal olmayan denklemlerin keyfiyet analizi zordur ve bazen mümkün değildir. Bu durumlarda sayısal analiz teknikleri uygulanır.

Kısmi diferansiyel denklemler, katsayıların durumlarına ve zamana ait türevin mevcudiyetine göre

1. şeklinde alt gruplara ayrılırlar.

Son iki tip denklem, zamana ait türevin mevcudiyetinden ötürü olarak isimlendirilir.

Modern uygulamaların zorlaması ile ortaya çıkan:

tiplerindeki denklemler yukardakilerden farklı olarak değerlendirilebilirler.

Sabit ortamlarda denklemler verilere göre:

1. Sınır değer

şeklinde sınıflandırılırlar. Sabit olmayan bir ortamda tanımlı denklemlere veya denir.

Birçok denklemden oluşan ilişkilere denklem sistemi adı verilir.

Diferansiyel Denklemlerin Tarihi

Diferansiyel denklemler, Isaac Newton ve Gottfried Leibniz'in Kalkülüs'ü ortaya atması ile başlar. Isaac Newton, 1671 yılında yayınlanan Methodus fluxionum et Serierum Infinitarum isimli kitabının ikinci bölümünde üç tip diferansiyel denklem tanımlamıştır:

• ${\displaystyle {\frac {dy}{dx}}=f(x)}$
• ${\displaystyle {\frac {dy}{dx}}=f(x,y)}$
• ${\displaystyle x_{1}{\frac {\partial y}{\partial x_{1}}}+x_{2}{\frac {\partial y}{\partial x_{2}}}=y}$

Tüm durumlarda ${\displaystyle y}$, ${\displaystyle x}$'in bilinmeyen bir fonksiyonu (ya da ${\displaystyle x_{1}}$ve ${\displaystyle x_{2}}$'nin) ve ${\displaystyle f}$ verilmiş bir fonksiyondur.

Isaac Newton bu ve diğer örnekleri kitabında Sonsuz seriler yöntemini kullanarak çözer ve çözümlerin yalnız bir tane olup olmadığını sorgular.

Jakob Bernouilli 1695 yılında Bernoulli diferansiyel denklemi'ni ortaya attı ve bu denklem şu formda bir Adi diferansiyel denklemdir:

${\displaystyle y\prime +P(x)y=Q(x)y^{n}}$

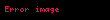
Sonraki yıllarda Gottfried Leibniz bu denklemin çözümünü, denklemi basitleştirerek bulmuştur.

Isı denklemi çözülerek oluşturulan bir pompa gövdesindeki ısı transferinin görselleştirilmesi.

Isı gövdenin içinde üretilir ve sınırda soğutularak sabit durumlu bir sıcaklık dağılımı sağlanır.

Uygulamalar

Diferansiyel denklemlerin etüdü, soyut ve uygulamalı matematik, fizik ve mühendislikte geniş bir alandır. Bu bilim dallarınının tümü, çeşitli türlerdeki diferansiyel denklemlerin özellikleri ile ilgilidir.

Soyut matematik, çözümlerin varlığına ve benzersizliğine odaklanırken, uygulamalı matematik, çözümlere yaklaşım yöntemlerinin kesin gerekçesini vurgular.

Diferansiyel denklemler, göksel hareketten köprü tasarımına ve nöronlar arasındaki etkileşimlere kadar neredeyse her fiziksel, teknik veya biyolojik sürecin modellenmesinde önemli bir rol oynar.

Gerçek hayat problemlerini çözmek için kullanılanlar gibi diferansiyel denklemler, mutlaka doğrudan çözülebilir olmayabilir, yani kapalı biçimli çözümleri yoktur. Bunun yerine, çözümler sayısal yöntemler kullanılarak yaklaşık olarak bulunabilir.

Fizik ve kimya ile ilgili birçok temel yasa diferansiyel denklemlerle formülleştirilebilir. Biyoloji ve ekonomi'de karmaşık sistemlerin davranışını model için diferansiyel denklemler kullanılır.

Diferansiyel denklemlerin matematiksel teorisi, ilk olarak denklemlerin ortaya çıktığı ve sonuçların uygulama bulduğu bilimlerle birlikte gelişti. Ancak, bazen oldukça farklı bilimsel alanlardan kaynaklanan çeşitli problemler, aynı diferansiyel denklemlere yol açabilir. Bu olduğunda, denklemlerin arkasındaki matematiksel teori, çeşitli doğa olaylarının arkasındaki birleştirici bir ilke olarak görülebilir. Örneğin atmosferdeki ışık ve sesin ve bir havuz yüzeyinde dalgaların yayılmasını düşünün. Hepsi aynı ikinci dereceden kısmi diferansiyel denklem olan dalga denklemi ile tanımlanabilir, bu ise ışık ve sesin dalga şekillerini sudaki bilinen dalgalar gibi düşünmemizi sağlar. Teorisi Joseph Fourier tarafından geliştirilen ısı iletimi, başka bir ikinci dereceden kısmi diferansiyel denklem olan ısı denklemi ile ifade edilir. Görünüşe göre farklı görünen birçok difüzyon işleminin aynı denklemle tanımlandığı ortaya çıkmıştır örn. finanstaki Black–Scholes denklemi, ısı denklemi ile ilişkilidir.

Doğada ve teknolojide çok sayıda doğa olayı, diferansiyel denklemler ve bunlara dayalı matematiksel modeller ile tanımlanabilir. Bazı tipik örnekler şunlardır:

• Birçok fiziksel teori, diferansiyel denklemlere dayanır: Newton mekaniği'nde hareket denklemleri veya salınımlar, yük bileşenlerinin davranışı, elektrodinamik, Maxwell denklemleri, kuantum mekaniği Schrödinger denklemi ile ifade edilir.
• Astronomi'de gök cisimlerinin yörüngeleri ve güneşin içindeki türbülans,
• Biyoloji'de büyüme, akışkanlar veya kaslar veya Evrim teorisindeki süreçler.
• Kimya'da reaksiyonların kinetiği,
• Elektrik mühendisliği'nde elektrik devreleri'nin enerji depolama elemanlarıyla davranışı,
• Diferansiyel geometri'de yüzeylerin davranışı,
• Akışkanlar mekaniği'nde bu akışların davranışı,
• Ekonomi'de ekonomik büyüme süreçlerinin analizi.
• Bilişim'de, resim-restorasyonu (resimlerden yazı veya logoların hesaplanması)

Diferansiyel denklemler alanı matematiğe belirleyici bir ivme kazandırdı. Güncel matematik araştırmalarının birçok bölümü farklı türdeki diferansiyel denklemlerin varlığı, tekliği ve kararlılık teorisi üzerinedir.

Yazılım

Maple: dsolve

Xcas: desolve(y'=k*y,y)

Dış bağlantılar

Vikikitap

Vikikitapta bu konu hakkında daha fazla bilgi var:

Linear Algebra

• MIT Professor Arthur Mattuck's Differential Equations Course Homepage 2 Ocak 2016 tarihinde Wayback Machine sitesinde .: MIT Course Website Kursu ve Türkçe tercümesi 5 Mart 2016 tarihinde Wayback Machine sitesinde ..

Kaynakça

1. ^ Dennis G. Zill (15 Mart 2012). A First Course in Differential Equations with Modeling Applications. Cengage Learning. ISBN . 17 Ocak 2020 tarihinde kaynağından . Erişim tarihi: 27 Ağustos 2020. 
2. ^ Newton, Isaac. (c.1671). Methodus Fluxionum et Serierum Infinitarum (The Method of Fluxions and Infinite Series), published in 1736 [Opuscula, 1744, Vol. I. p. 66].
3. ^ Bernoulli, Jacob (1695), "Explicationes, Annotationes & Additiones ad ea, quae in Actis sup. de Curva Elastica, Isochrona Paracentrica, & Velaria, hinc inde memorata, & paratim controversa legundur; ubi de Linea mediarum directionum, alliisque novis", Acta Eruditorum
4. ^ Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard (1993), Solving ordinary differential equations I: Nonstiff problems, Berlin, New York: Springer-Verlag,
5. ^ Peterson, Ivars (2002). "Filling in Blanks". Science News. Society for Science &#38. 161 (19): 299-300. doi:10.2307/4013521. 27 Haziran 2009 tarihinde kaynağından . Erişim tarihi: 11 Mayıs 2008. 
6. ^ . 23 Kasım 2013 tarihinde kaynağından arşivlendi. 
7. ^ "Symbolic algebra and Mathematics with Xcas" (PDF). 29 Temmuz 2014 tarihinde kaynağından (PDF).