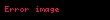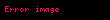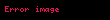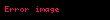Matematikte, Poisson denklemi elektrostatik, makine mühendisliği ve teorik fizik'de geniş kullanım alanına sahip eliptik türdeki Kısmi diferansiyel denklemlerdir. Fransız matematikçi, ve fizikçi olan Siméon Denis Poisson'dan sonra isimlendirilmiştir. Poisson denklemi
Burada Laplasyene ve f ve φ ise Çokkatlıda gerçek veya Karmaşık-değerli fonksiyonlara karşılık gelmektedir. Çokkatlı öklid uzayı olduğu zaman, Laplasyen olarak belirtilir ve Poisson denklemi genel olarak
şeklinde yazılır. 3 boyutlu Kartezyen koordinat sisteminde
formunu alır. f sıfır olduğunda denklem;
halini alır. Bu Poisson denklemi, Green fonksiyonu kullanılarak çözülebilir; Green Fonksiyonunun Poisson denklemi için genel çözümünü Sönümlü Poisson denklemi başlığında verilmiştir. Nümerik çözüm için çok fazla değişik türden metot bulunmaktadır; rahatlatma metodu, yinelemeli algoritma sadece bir örnek...
Elektrostatik
Elektrostatiğin köşe taşlarından biri de Poisson denklemleri ile açıklanan problemlerin çözümünü ortaya atıp çözmektir. Verilmiş bir yük dağılımı için Elektriksel gerilimi bulmak için genelde kullandığımız yol bu olduğu için, φ'yi verilmiş f cinsinden bulmak önemli pratik bir sorundur.
Elektrostatikteki Poisson denkleminin türeyişi şu şekildedir. Uluslararası Birimler Sisteminin Öklid uzayında kullanıldığını var sayarsak ve differansiyel kontrol hacimdeki elektrik için Gauss Yasası ile başlarsak:
, Diverjansa
,
, yük yoğunluğuna (yani dışarıdan getirilmiş yüklere) tekamül etmektedir.
Ortamın lineer, izotropik ve homojen olduğunu kabul edersek;
, ortamın geçirgenliği
, elektrik alan'dır.
Yerine koyma ve sadeleştirme işlemlerinden sonra;
elde ederiz. Değişken bir manyetik alan, 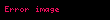
, Rotasyonele
ise zamana karşılık gelmektedir.
Elektrik Alanın Rotasyoneli sıfır olduğundan, o bir skaler elektrik potansiyel birler elektrik potansiyel olarak tanımlanır.
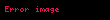
Potansiyel için Poisson denklemini çözmek yük yoğunluğu dağılımının bilinmesini gerektirir. Eğer yük yoğunluğu sıfır ise denklem Laplace denklemine dönüşür. Eğer ki yük yoğunluğu Boltzmann dağılımına tekamül ederse denklem halini alır. Poisson Boltzmann denklemi gelişmesinde büyük rol oynar.
(Not: Yukarıdaki tartışma manyetik alanın zamanla değişmediğini kabullenim olarak alsa da aynı kullanıldığı sürece zamanla gerçekten bir değişim olsa bile Poisson denklemi ortaya çıkar. Yalnız, genel bağlamda 
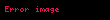
Gauss yük yoğunluğunun potansiyeli
Eğer ki durgun küresel simetrik bir Gauss yük yoğunluğu 
burada Q toplam yüktür. Dolayısıyla Poisson denkleminin çözümü φ (r),
,
burada 
ki burada erf(x) hata fonksiyonuna tekamül etmektedir. Bu çözüm bariz bir biçimde 

Ayrıca bakınız
Kaynakça
- (PDF). EqWorld: The World of Mathematical Equations. 25 Mayıs 2005 tarihinde kaynağından (PDF) arşivlendi..
- L.C. Evans, Partial Differential Equations, American Mathematical Society, Providence, 1998.
- A.D. Polyanin, Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC Press, Boca Raton, 2002.
Dış bağlantılar
- . PlanetMath. 18 Şubat 2012 tarihinde kaynağından arşivlendi..
- . model gallery. 8 Mart 2012 tarihinde kaynağından arşivlendi..
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte Poisson denklemi elektrostatik makine muhendisligi ve teorik fizik de genis kullanim alanina sahip eliptik turdeki Kismi diferansiyel denklemlerdir Fransiz matematikci ve fizikci olan Simeon Denis Poisson dan sonra isimlendirilmistir Poisson denklemi Df f displaystyle Delta varphi f Burada D displaystyle Delta Laplasyene ve f ve f ise Cokkatlida gercek veya Karmasik degerli fonksiyonlara karsilik gelmektedir Cokkatli oklid uzayi oldugu zaman Laplasyen 2 displaystyle nabla 2 olarak belirtilir ve Poisson denklemi genel olarak 2f f displaystyle nabla 2 varphi f seklinde yazilir 3 boyutlu Kartezyen koordinat sisteminde 2 x2 2 y2 2 z2 f x y z f x y z displaystyle left frac partial 2 partial x 2 frac partial 2 partial y 2 frac partial 2 partial z 2 right varphi x y z f x y z formunu alir f sifir oldugunda denklem Df 0 displaystyle Delta varphi 0 halini alir Bu Poisson denklemi Green fonksiyonu kullanilarak cozulebilir Green Fonksiyonunun Poisson denklemi icin genel cozumunu Sonumlu Poisson denklemi basliginda verilmistir Numerik cozum icin cok fazla degisik turden metot bulunmaktadir rahatlatma metodu yinelemeli algoritma sadece bir ornek ElektrostatikElektrostatigin kose taslarindan biri de Poisson denklemleri ile aciklanan problemlerin cozumunu ortaya atip cozmektir Verilmis bir yuk dagilimi icin Elektriksel gerilimi bulmak icin genelde kullandigimiz yol bu oldugu icin f yi verilmis f cinsinden bulmak onemli pratik bir sorundur Elektrostatikteki Poisson denkleminin tureyisi su sekildedir Uluslararasi Birimler Sisteminin Oklid uzayinda kullanildigini var sayarsak ve differansiyel kontrol hacimdeki elektrik icin Gauss Yasasi ile baslarsak D rf displaystyle mathbf nabla cdot mathbf D rho f displaystyle mathbf nabla cdot Diverjansa D displaystyle mathbf D rf displaystyle rho f yuk yogunluguna yani disaridan getirilmis yuklere tekamul etmektedir dd Ortamin lineer izotropik ve homojen oldugunu kabul edersek D eE displaystyle mathbf D varepsilon mathbf E e displaystyle varepsilon ortamin gecirgenligi E displaystyle mathbf E elektrik alan dir dd Yerine koyma ve sadelestirme islemlerinden sonra E rfe displaystyle mathbf nabla cdot mathbf E frac rho f varepsilon elde ederiz Degisken bir manyetik alan B displaystyle mathbf B olmadigi zaman Faraday Lenz yasasi geregince E B t 0 displaystyle nabla times mathbf E dfrac partial mathbf B partial t 0 displaystyle nabla times Rotasyonele t displaystyle t ise zamana karsilik gelmektedir dd Elektrik Alanin Rotasyoneli sifir oldugundan o bir skaler elektrik potansiyel birler elektrik potansiyel olarak tanimlanir E f displaystyle mathbf E nabla varphi E displaystyle mathbf E yi yerine koyma metodu ile yok edersek Poisson denkleminin bir formunu elde ederiz f 2f rfe displaystyle nabla cdot nabla varphi nabla 2 varphi frac rho f varepsilon Potansiyel icin Poisson denklemini cozmek yuk yogunlugu dagiliminin bilinmesini gerektirir Eger yuk yogunlugu sifir ise denklem Laplace denklemine donusur Eger ki yuk yogunlugu Boltzmann dagilimina tekamul ederse denklem halini alir Poisson Boltzmann denklemi gelismesinde buyuk rol oynar Not Yukaridaki tartisma manyetik alanin zamanla degismedigini kabullenim olarak alsa da ayni kullanildigi surece zamanla gercekten bir degisim olsa bile Poisson denklemi ortaya cikar Yalniz genel baglamda f displaystyle varphi hesaplamak artik E displaystyle mathbf E yi hesaplamak icin yeterli degildir cunku ikincisi ayni zamanda baglidir ki bu da bagimsiz olarak hesaplanmalidir Gauss yuk yogunlugunun potansiyeli Eger ki durgun kuresel simetrik bir Gauss yuk yogunlugu rf r displaystyle rho f r var ise rf r Qs32p3e r2 2s2 displaystyle rho f r frac Q sigma 3 sqrt 2 pi 3 e r 2 2 sigma 2 burada Q toplam yuktur Dolayisiyla Poisson denkleminin cozumu f r 2f rfe displaystyle nabla 2 varphi rho f over varepsilon burada f r displaystyle varphi r soyle gosterilir f r 14peQrerf r2s displaystyle varphi r 1 over 4 pi varepsilon frac Q r mbox erf left frac r sqrt 2 sigma right ki burada erf x hata fonksiyonuna tekamul etmektedir Bu cozum bariz bir bicimde 2f displaystyle nabla 2 varphi yi hesaplayarak kontrol edilebilir Dikkate alinmali ki tahmin edildigi sekilde s den cok buyuk bir r icin erf fonksiyonu 1 e ve potansiyel noktasal yuk potansiyeli f r 14pe0Qr displaystyle 1 over 4 pi varepsilon 0 Q over r e yaklasmaktadir Ayrica erf fonksiyonu kendi argumani arttikca 1 e cok hizli sekilde yaklasmaktadir pratikte r gt 3s icin goreli hata binde birden kucuktur Ayrica bakinizKaynakca PDF EqWorld The World of Mathematical Equations 25 Mayis 2005 tarihinde kaynagindan PDF arsivlendi L C Evans Partial Differential Equations American Mathematical Society Providence 1998 ISBN 0 8218 0772 2 A D Polyanin Handbook of Linear Partial Differential Equations for Engineers and Scientists Chapman amp Hall CRC Press Boca Raton 2002 ISBN 1 58488 299 9Dis baglantilar PlanetMath 18 Subat 2012 tarihinde kaynagindan arsivlendi model gallery 8 Mart 2012 tarihinde kaynagindan arsivlendi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans