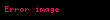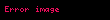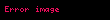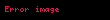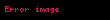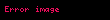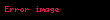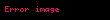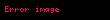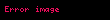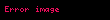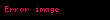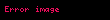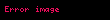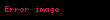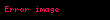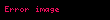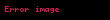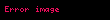Matematik'te, digama fonksiyonu gama fonksiyonu'nun olarak tanımlanır:

Bu poligama fonksiyonu'nun ilkidir.
Harmonik sayılar ile ilişkisi
Digamma 'u, sıklıkla ψ0(x), ψ0(x) veya 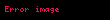
Burada Hn is the n 'inci harmonik sayıdır ve γ Euler-Mascheroni sabiti'dir. yarı tam sayı değerleri için, açılım
Integral Gösterimleri
integral gösterimi
şeklindedir.
reel kısmının pozitif değerleri için geçerlidir.Bunu şöyle yazabiliriz
harmonik sayılar için Euler integrali'dir .
Seri formülü
Digamma negatif tam sayılar dışında kompleks düzlemde hesaplanabilir (Abramowitz and Stegun 6.3.16), yardımıyla
Taylor serisi
Digama Taylor serisi'nde z=1 verilerek elde edilen bir , . Burada
,
yakınsaklık için |z|<1. Burada, 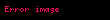
Newton serisi
Digama için Euler integral formülü ile :
Burada 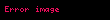
Refleksiyon formülü
Digama fonksiyonunu Gama fonksiyonu'na benzer bir karşılar
Özyineleme formülü
'ne dayanılarak Digamma fonksiyonu
Böylece,1/x için "teleskop" denilebilir, bu nedenle
Burada Δ 'dür. Aşağıdaki formülle 'nin kısmi toplamı 'ne karşı gelir ,
burada 
Daha genel bir ifade,
Gauss toplamı
Digama'nın formu
şeklindedir.
Tam sayılar için 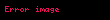
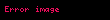
ve genelleştirilmiş şekli
Burada q 'nun doğal sayı ve 1-qa 'nın doğal sayı olmadığı varsayılmıştır. .
Gauss'un digama teoremi
Pozitif tam sayılar m ve k (m < k) şartıyla,digama fonksiyonunun Temel fonksiyon olarak ifadesi
Hesaplama & yaklaşıklık
J.M. Bernardo AS 103 algoritmiyle ile x, gerçel bir sayı olmak üzere digama fonksiyonu hesaplanabilir,
veya
n tam sayı, B(n) n 'inci Bernouilli sayısı ve 
Özel değerler
Digama fonksiyonu için bazı özel değerler:
Ayrıca bakınız
Kaynakça
- Abramowitz, M. and Stegun, I. A. (Eds.). "Psi (Digamma) Function." §6.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 258–259, 1972. See section §6.42 Eylül 2009 tarihinde Wayback Machine sitesinde .
- Eric W. Weisstein, Digamma function (MathWorld)
Dış bağlantılar
- Cephes8 Aralık 2009 tarihinde Wayback Machine sitesinde . - C and C++ language special functions math library
- [1] 27 Eylül 2011 tarihinde Wayback Machine sitesinde . - Bernardo Statistical algorithm Psi(digamma function) computation, pp. 1
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematik te digama fonksiyonu gama fonksiyonu nun olarak tanimlanir kompleks duzlem de ps s displaystyle psi s Digama fonksiyonu renkli bir s displaystyle s noktasina karsi kodlanan deger ps s displaystyle psi s Guclu renkler sifira yakin degerleri ve tonlari gosteren ise argument degerleridir ps x ddxln G x G x G x displaystyle psi x frac d dx ln Gamma x frac Gamma x Gamma x Bu poligama fonksiyonu nun ilkidir Harmonik sayilar ile iliskisiDigamma u siklikla ps0 x ps0 x veya ϝ displaystyle digamma eski yunan harfleriyle digama nin gosterimi Ϝ dir seklinde gosterilir la iliskisi ps n Hn 1 g displaystyle psi n H n 1 gamma Burada Hn is the n inci harmonik sayidir ve g Euler Mascheroni sabiti dir yari tam sayi degerleri icin acilim ps n 12 g 2ln 2 k 1n22k 1 displaystyle psi left n frac 1 2 right gamma 2 ln 2 sum k 1 n frac 2 2k 1 Integral Gosterimleriintegral gosterimi ps x 0 e tt e xt1 e t dt displaystyle psi x int 0 infty left frac e t t frac e xt 1 e t right dt seklindedir x displaystyle x reel kisminin pozitif degerleri icin gecerlidir Bunu soyle yazabiliriz ps s 1 g 011 xs1 xdx displaystyle psi s 1 gamma int 0 1 frac 1 x s 1 x dx harmonik sayilar icin Euler integrali dir Seri formuluDigamma negatif tam sayilar disinda kompleks duzlemde hesaplanabilir Abramowitz and Stegun 6 3 16 yardimiyla ps z 1 g n 1 zn n z z 1 2 3 displaystyle psi z 1 gamma sum n 1 infty left frac z n n z right z neq 1 2 3 Taylor serisiDigama Taylor serisi nde z 1 verilerek elde edilen bir Burada ps z 1 g k 1 z k 1 z k displaystyle psi z 1 gamma sum k 1 infty zeta k 1 z k yakinsaklik icin z lt 1 Burada z n displaystyle zeta n Riemann zeta fonksiyonu dur Bu seri ile kolayca Hurwitz zeta fonksiyonu na karsilik gelen Taylor serisi elde edilebilir Newton serisiDigama icin Euler integral formulu ile ps s 1 g k 1 1 kk sk displaystyle psi s 1 gamma sum k 1 infty frac 1 k k s choose k Burada sk displaystyle textstyle s choose k dir Refleksiyon formuluDigama fonksiyonunu Gama fonksiyonu na benzer bir karsilar ps 1 x ps x pcot px displaystyle psi 1 x psi x pi cot left pi x right Ozyineleme formulu ne dayanilarak Digamma fonksiyonu ps x 1 ps x 1x displaystyle psi x 1 psi x frac 1 x Boylece 1 x icin teleskop denilebilir bu nedenle D ps x 1x displaystyle Delta psi x frac 1 x Burada D dur Asagidaki formulle nin kismi toplami ne karsi gelir ps n Hn 1 g displaystyle psi n H n 1 gamma burada g displaystyle gamma Euler Mascheroni sabiti dir Daha genel bir ifade ps x 1 g k 1 1k 1x k displaystyle psi x 1 gamma sum k 1 infty left frac 1 k frac 1 x k right Gauss toplamiDigama nin formu 1pk n 1ksin 2pnmk ps nk z 0 mk B1 mk 12 mk displaystyle frac 1 pi k sum n 1 k sin left frac 2 pi nm k right psi left frac n k right zeta left 0 frac m k right B 1 left frac m k right frac 1 2 frac m k seklindedir Tam sayilar icin 0 lt m lt k displaystyle 0 lt m lt k Burada z s q Hurwitz zeta fonksiyonu dur ve Bn x displaystyle B n x i dur nin ozel bir durumu n 1kps nk k g log k displaystyle sum n 1 k psi left frac n k right k gamma log k ve genellestirilmis sekli p 0q 1ps a p q q ps qa ln q displaystyle sum p 0 q 1 psi a p q q psi qa ln q Burada q nun dogal sayi ve 1 qa nin dogal sayi olmadigi varsayilmistir Gauss un digama teoremiPozitif tam sayilar m ve k m lt k sartiyla digama fonksiyonunun Temel fonksiyon olarak ifadesi ps mk g ln 2k p2cot mpk 2 n 1 k 1 2 cos 2pnmk ln sin npk displaystyle psi left frac m k right gamma ln 2k frac pi 2 cot left frac m pi k right 2 sum n 1 lceil k 1 2 rceil cos left frac 2 pi nm k right ln left sin left frac n pi k right right Hesaplama amp yaklasiklikJ M Bernardo AS 103 algoritmiyle ile x gercel bir sayi olmak uzere digama fonksiyonu hesaplanabilir ps x ln x 12x 112x2 1120x4 1252x6 O 1x8 displaystyle psi x ln x frac 1 2x frac 1 12x 2 frac 1 120x 4 frac 1 252x 6 O left frac 1 x 8 right veya ps x ln x 12x n 1 z 1 2n x2n displaystyle psi x ln x frac 1 2x sum n 1 infty frac zeta 1 2n x 2n ps x ln x 12x n 1 B 2n 2n x2n displaystyle psi x ln x frac 1 2x sum n 1 infty frac B 2n 2n x 2n n tam sayi B n n inci Bernouilli sayisi ve z n displaystyle zeta n Riemann zeta fonksiyonu dur Ozel degerlerDigama fonksiyonu icin bazi ozel degerler ps 1 g displaystyle psi 1 gamma ps 12 2ln 2 g displaystyle psi left frac 1 2 right 2 ln 2 gamma ps 13 p23 32ln 3 g displaystyle psi left frac 1 3 right frac pi 2 sqrt 3 frac 3 2 ln 3 gamma ps 14 p2 3ln 2 g displaystyle psi left frac 1 4 right frac pi 2 3 ln 2 gamma ps 16 p23 2ln 2 32ln 3 g displaystyle psi left frac 1 6 right frac pi 2 sqrt 3 2 ln 2 frac 3 2 ln 3 gamma ps 18 p2 4ln 2 12 p ln 2 2 ln 2 2 g displaystyle psi left frac 1 8 right frac pi 2 4 ln 2 frac 1 sqrt 2 left pi ln 2 sqrt 2 ln 2 sqrt 2 right gamma Ayrica bakinizMatematiksel fonksiyonlarin listesi Trigama fonksiyonuKaynakcaAbramowitz M and Stegun I A Eds Psi Digamma Function 6 3 in Handbook of Mathematical Functions with Formulas Graphs and Mathematical Tables 9th printing New York Dover pp 258 259 1972 See section 6 42 Eylul 2009 tarihinde Wayback Machine sitesinde Eric W Weisstein Digamma function MathWorld Dis baglantilarCephes8 Aralik 2009 tarihinde Wayback Machine sitesinde C and C language special functions math library 1 27 Eylul 2011 tarihinde Wayback Machine sitesinde Bernardo Statistical algorithm Psi digamma function computation pp 1
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans