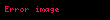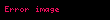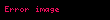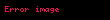Medyan (ya da ortanca) bir anakütle ya da örneklem veri serisini küçükten büyüğe doğru sıraladığımızda, seriyi ortadan ikiye ayıran değere denir. İstatistiğin bir alt dalı olan betimsel istatistikde medyan bir merkezsel konum ölçüsü kabul edilir.
Merkezsel konum olarak medyan
Bir olasılık dağılımı simetrik olmayıp, çarpıklık gösteriyorsa, medyan, aritmetik ortalamadan daha uygun bir merkezsel konum ölçüsüdür. Simetrik olmama, sıralanmış veri değerleri için ya en küçük değerlerin ya da en büyük değerlerin diğerlerinden çok daha fazla uzaklaşması ile ortaya çıkar. Bu beklenmedik küçük veya büyük değerlere aykırı değer (outlier) adı verilir. Eğer veri dağılımı asitmetrik olan aykırı değerler kapsıyorsa, medyan aritmetik ortalamaya nazaran daha güçlü (robust) bir merkezsel konum ölçüsü halini alır.
Medyan değeri hesaplanması
Veri sayıları küçükten büyüğe doğru sıralandıktan sonra, n gözlem sayısı olmak üzere, medyan değerinin bu seri içindeki sıra numarası şu şekilde bulunur:
Eğer gözlem sayısı tek ise medyanın sıra numarası bir tam sayı olacaktır ve doğrudan medyan bulunur. Eğer gözlem sayısı çift ise medyanın sıra numarası ½ li bir sayı çıkar. Bu durumda bu sayının etrafındaki iki değerin aritmetik ortalaması medyandır.
- Örnek
1,3,4,5,7,8,13 dizisinin medyanı 4. sıradaki eleman olan 5'tir.
2,4,6,8 dizisinin medyan pozisyonu 2.5'tir. Bu durumda 2. ve 3. elemanların aritmetik ortalaması yani (4+6)/2=5 medyan değeridir.
Gözlem sayısı küçükse, gözlem değerlerinin sıralaması elle kolay olarak yapılabilmekte ve bu hesaplama kolaylığı merkezsel konum ölçüsü olarak medyanın tercih edilmesine bir neden olmaktadır. Ancak gözlem sayısı n artıkça, sıralama işlemleri gittikçe zorlaşmaktadır; ayrıca basit el hesap makinaları ile sıralama yapmak imkanı olmamaktadır. Bilgisayar kullanılmadan ve elle yapılan işlemler kullanarak büyük gözlem sayılı verilerinin sıralanması zorluğu nedeni ile medyan büyük veri kullanılması gerektiren araştırmalarda kullanılmamıştır. Ama bilgisayarların gelişmesi ile medyan kullanılmasının bu dezavantajı kaybolmuştur. Bilgisayarla yapılan veri sıralanması için, özellikle çok büyük gözlem sayıda veri için özel hızlı sıralama algoritmaları kullanılmaktadır. Bu sıralama algoritmalarında genellikle (n log n) işlem yapılmaktadır ama özel kullanılması ile sadece n işlem gerekmektedir.
Çokluk dağılımları için medyan değerinin hesaplanması
Veri değerleri gruplanmış ve çokluk dağılımları olarak verilmişler ise, medyan, gözlem sayısında N/2 inci değerin denk düştüğü sınıftadır ve interpolasyon ile ortaya çıkartılan formülü şu şekilde verilir:
- L: Medyan sınıfın alt değeri
- c: Medyan sınıfın aralığı
- f: Medyan sınıfın frekansı
- N: Toplam birim sayısı
- d: Medyan sınıftan bir önceki sınıfın birikimli frekansı.
Olasılık dağılımları için medyanlar
Reel doğrusu üzerinde olan ve F fonksiyonu ile ifade edilen yığmalı dağılım fonksiyonu gösteren herhangi bir olasılık dağılımı için, veya sürekli olması özelliğine bakılmadan, medyan değeri m şu eşitsizlik ifadelerine her zaman uyar:
veya
Belirli parametreleri olan belirli dağılımların medyanları hakkında şunlar söylenebilir:
- Ortalama değeri μ ve varyansı σ2 olan bir normal dağılım için medyan değeri μ olur. Gerçekten normal dağılım simetrik çan şeklinde olduğundan ortalama=medyan=mod olur.
- [a b] aralığında bulunan bir sürekli tekdüze dağılım için medyan değeri (a + b) / 2 olup bu ortalama değerine de eşittir.
- Konum parametresi x0 ve ölçek parametresi y de x0 olan Cauchy dağılımı için medyan değeri konum parametresine eşittir.
- Şekil parametresi k ve ölçek parametresi
olan bir Weibull dağılımı için medyan değeri
olur.
Özellikleri
- Optimal olma özelliği
Medyan, mutlak dağılmaların ortalamalarının en küçük değerini bulan bir merkezsel noktadır. Olasılık kuramının özel terimlerine göre
ifadesini en küçük yapan c değeri için, X rassal değişkenin olasılık dağılımının medyanıdır. Dikkat edilmesi gerekir ki, c her zaman tek değildir ve onun için genellikle kesinlikle tanımlanamaz.
- Sürekli bir olasılık dağılımı için, medyan sayı değeri ile ortalama sayı değeri arasında bir standart sapmaya eşit bir fark vardır.
- Medyan 2inci dörttebirlik, 5inci ondabirlik ve 50inci yüzdebirlik'e eşittir.
- Genellikle medyan bir yanlı kestirimcidir.
Ayrıca bakınız
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Medyan ya da ortanca bir anakutle ya da orneklem veri serisini kucukten buyuge dogru siraladigimizda seriyi ortadan ikiye ayiran degere denir Istatistigin bir alt dali olan betimsel istatistikde medyan bir merkezsel konum olcusu kabul edilir Merkezsel konum olarak medyanBir olasilik dagilimi simetrik olmayip carpiklik gosteriyorsa medyan aritmetik ortalamadan daha uygun bir merkezsel konum olcusudur Simetrik olmama siralanmis veri degerleri icin ya en kucuk degerlerin ya da en buyuk degerlerin digerlerinden cok daha fazla uzaklasmasi ile ortaya cikar Bu beklenmedik kucuk veya buyuk degerlere aykiri deger outlier adi verilir Eger veri dagilimi asitmetrik olan aykiri degerler kapsiyorsa medyan aritmetik ortalamaya nazaran daha guclu robust bir merkezsel konum olcusu halini alir Medyan degeri hesaplanmasi Veri sayilari kucukten buyuge dogru siralandiktan sonra n gozlem sayisi olmak uzere medyan degerinin bu seri icindeki sira numarasi su sekilde bulunur Medyanpozisyonu n 1 2 displaystyle Medyanpozisyonu frac n 1 2 Eger gozlem sayisi tek ise medyanin sira numarasi bir tam sayi olacaktir ve dogrudan medyan bulunur Eger gozlem sayisi cift ise medyanin sira numarasi li bir sayi cikar Bu durumda bu sayinin etrafindaki iki degerin aritmetik ortalamasi medyandir Ornek 1 3 4 5 7 8 13 dizisinin medyani 4 siradaki eleman olan 5 tir 2 4 6 8 dizisinin medyan pozisyonu 2 5 tir Bu durumda 2 ve 3 elemanlarin aritmetik ortalamasi yani 4 6 2 5 medyan degeridir Gozlem sayisi kucukse gozlem degerlerinin siralamasi elle kolay olarak yapilabilmekte ve bu hesaplama kolayligi merkezsel konum olcusu olarak medyanin tercih edilmesine bir neden olmaktadir Ancak gozlem sayisi n artikca siralama islemleri gittikce zorlasmaktadir ayrica basit el hesap makinalari ile siralama yapmak imkani olmamaktadir Bilgisayar kullanilmadan ve elle yapilan islemler kullanarak buyuk gozlem sayili verilerinin siralanmasi zorlugu nedeni ile medyan buyuk veri kullanilmasi gerektiren arastirmalarda kullanilmamistir Ama bilgisayarlarin gelismesi ile medyan kullanilmasinin bu dezavantaji kaybolmustur Bilgisayarla yapilan veri siralanmasi icin ozellikle cok buyuk gozlem sayida veri icin ozel hizli siralama algoritmalari kullanilmaktadir Bu siralama algoritmalarinda genellikle n log n islem yapilmaktadir ama ozel kullanilmasi ile sadece n islem gerekmektedir Cokluk dagilimlari icin medyan degerinin hesaplanmasi Veri degerleri gruplanmis ve cokluk dagilimlari olarak verilmisler ise medyan gozlem sayisinda N 2 inci degerin denk dustugu siniftadir ve interpolasyon ile ortaya cikartilan formulu su sekilde verilir Medyan L cf N2 d displaystyle Medyan L frac c f left frac N 2 d right L Medyan sinifin alt degeri c Medyan sinifin araligi f Medyan sinifin frekansi N Toplam birim sayisi d Medyan siniftan bir onceki sinifin birikimli frekansi Olasilik dagilimlari icin medyanlarReel dogrusu uzerinde olan ve F fonksiyonu ile ifade edilen yigmali dagilim fonksiyonu gosteren herhangi bir olasilik dagilimi icin veya surekli olmasi ozelligine bakilmadan medyan degeri m su esitsizlik ifadelerine her zaman uyar P X m 12 P X m 12 displaystyle operatorname P X leq m geq frac 1 2 quad land quad operatorname P X geq m geq frac 1 2 veya mdF x 12 m dF x 12 displaystyle int infty m mathrm d F x geq frac 1 2 quad land quad int m infty mathrm d F x geq frac 1 2 Belirli parametreleri olan belirli dagilimlarin medyanlari hakkinda sunlar soylenebilir Ortalama degeri m ve varyansi s2 olan bir normal dagilim icin medyan degeri m olur Gercekten normal dagilim simetrik can seklinde oldugundan ortalama medyan mod olur a b araliginda bulunan bir surekli tekduze dagilim icin medyan degeri a b 2 olup bu ortalama degerine de esittir Konum parametresi x0 ve olcek parametresi y de x0 olan Cauchy dagilimi icin medyan degeri konum parametresine esittir Sekil parametresi k ve olcek parametresi l displaystyle lambda olan bir Weibull dagilimi icin medyan degeri l ln 2 1 k displaystyle lambda ln 2 1 k olur OzellikleriOptimal olma ozelligi Medyan mutlak dagilmalarin ortalamalarinin en kucuk degerini bulan bir merkezsel noktadir Olasilik kuraminin ozel terimlerine gore E X c displaystyle E left X c right ifadesini en kucuk yapan c degeri icin X rassal degiskenin olasilik dagiliminin medyanidir Dikkat edilmesi gerekir ki c her zaman tek degildir ve onun icin genellikle kesinlikle tanimlanamaz Surekli bir olasilik dagilimi icin medyan sayi degeri ile ortalama sayi degeri arasinda bir standart sapmaya esit bir fark vardir Medyan 2inci dorttebirlik 5inci ondabirlik ve 50inci yuzdebirlik e esittir Genellikle medyan bir yanli kestirimcidir Ayrica bakinizGeometrik medyan Merkezsel konum olculeriKaynakca Istatistik 3 baski Yuzer Ali Fuat Eskisehir Anadolu Universitesi 2006 ss 48 53 ISBN 975 06 0183 1 OCLC 567334808
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans