Matematikte logaritmik ortalama, iki pozitif gerçek sayının farkının bu sayıların doğal logaritmalarının farkına oranı olarak tanımlanır. Bu hesaplama, ısı ve kütle transferi içeren mühendislik problemlerinde kullanılabilir.

Tanım
Logaritmik ortalama şu şekilde tanımlanır: 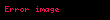
İlgili eşitsizlikler
İki sayının logaritmik ortalaması, bu sayıların aritmetik ortalamasından ve 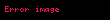
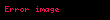
Tanımın elde edilmesi
Ortalama değer teoremi yorumu
Ortalama değer teoremine göre, herhangi bir (x, y) bir fonksiyonun türevinin kesen doğrunun eğimine eşit olmasını sağlayan bir 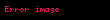
Logaritmik ortalama, 
eşitliği nedeniyle,
İntegral yorumu
Logaritmik ortalama, üstel bir eğrinin altında kalan alan olarak da yorumlanabilir:
Bu yorum, logaritmik ortalamanın bazı temel özelliklerinin kolayca elde edilmesini sağlar. Örneğin, üstel fonksiyon bir fonksiyon olduğu için 1 uzunluğundaki bir aralıktaki integral, 


Logaritmik ortalamanın diğer iki faydalı integral gösterimi, 

Tanımın genelleştirilmesi
Ortalama değer teoremi yorumu
Logaritmik ortalama, göz önüne alınarak doğal logaritma fonksiyonunun 


Bu genelleştirme, 
İntegral yorumu
Logaritmik ortalamanın integral yorumu da daha fazla değişkene genelleştirilebilir, ancak bu durum farklı bir sonuca yol açar. 

Bu tanım, üstel fonksiyonun bölünmüş farkları kullanılarak aşağıdaki gibi basitleştirilebilir:
Diğer ortalamalarla ilişkisi
Sıkça karşılaşılan bazı ortalama çeşitleri, logaritmik ortalama cinsinden ifade edilebilir.
- Aritmetik ortalama:
- Geometrik ortalama:
- Harmonik ortalama:
Ayrıca bakınız
Kaynaklar
- ^ B. C. Carlson (1966). "Some inequalities for hypergeometric functions". Proc. Amer. Math. Soc. 17: 32-39. doi:10.1090/s0002-9939-1966-0188497-6.
- ^ B. Ostle (1957). "A comparison of two means". Proc. Montana Acad. Sci. 17: 69-70.
- ^ Tung-Po Lin. "The Power Mean and the Logarithmic Mean". The American Mathematical Monthly. doi:10.1080/00029890.1974.11993684.
Konuyla ilgili yayınlar
- Stolarsky, Kenneth (1975). "Generalizations of the logarithmic mean". . 48 (2): 87-92. doi:10.2307/2689825.
Dış bağlantılar
- Eric W. Weisstein, Arithmetic-Logarithmic-Geometric-Mean Inequality (MathWorld)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte logaritmik ortalama iki pozitif gercek sayinin farkinin bu sayilarin dogal logaritmalarinin farkina orani olarak tanimlanir Bu hesaplama isi ve kutle transferi iceren muhendislik problemlerinde kullanilabilir Logaritmik ortalamanin degerlerini gosteren uc boyutlu grafik TanimLogaritmik ortalama su sekilde tanimlanir x y displaystyle x y pozitif gercek sayilar olmak uzere Mlm x y lim 3 h x y h 3ln h ln 3 xx y ise y xln y ln x x y ise displaystyle begin aligned M text lm x y amp lim xi eta to x y frac eta xi ln eta ln xi 6pt amp begin cases x amp x y text ise frac y x ln y ln x amp x neq y text ise end cases end aligned Ilgili esitsizliklerIki sayinin logaritmik ortalamasi bu sayilarin aritmetik ortalamasindan ve 1 3 displaystyle 1 3 uncu dereceden genellestirilmis ortalamasindan daha buyuk olamaz Ayni zamanda bu ortalama sayilarin geometrik ortalamasindan daha kucuk de olamaz Iki sayinin birbirine esit oldugu durumda ise bu dort ortalama cesidi de birbirine esit olur Baska bir deyisle her x y displaystyle x y pozitif gercek sayilari icin asagidaki esitsizlik gecerlidir xy Mlm x y x1 3 y1 32 3 x y2 displaystyle sqrt xy leq M text lm x y leq left frac x 1 3 y 1 3 2 right 3 leq frac x y 2 Tanimin elde edilmesiOrtalama deger teoremi yorumu Ortalama deger teoremine gore herhangi bir x y bir fonksiyonun turevinin kesen dogrunun egimine esit olmasini saglayan bir 3 displaystyle xi degeri bulunur 3 x y f 3 f x f y x y displaystyle exists xi in x y f xi frac f x f y x y Logaritmik ortalama f displaystyle f fonksiyonunun dogal logaritma oldugu durumda 3 displaystyle xi nin alacagi deger olarak tanimlanabilir 13 ln x ln y x y displaystyle frac 1 xi frac ln x ln y x y esitligi nedeniyle 3 x yln x ln y displaystyle xi frac x y ln x ln y Integral yorumu Logaritmik ortalama ustel bir egrinin altinda kalan alan olarak da yorumlanabilir L x y 01x1 tyt dt 01 yx tx dt x 01 yx tdt xln yx yx t t 01 xln yx yx 1 y xln yx y xln y ln x displaystyle begin aligned L x y amp int 0 1 x 1 t y t mathrm d t int 0 1 left frac y x right t x mathrm d t x int 0 1 left frac y x right t mathrm d t 3pt amp left frac x ln left frac y x right left frac y x right t right t 0 1 frac x ln left frac y x right left frac y x 1 right frac y x ln left frac y x right 3pt amp frac y x ln left y right ln left x right end aligned Bu yorum logaritmik ortalamanin bazi temel ozelliklerinin kolayca elde edilmesini saglar Ornegin ustel fonksiyon bir fonksiyon oldugu icin 1 uzunlugundaki bir araliktaki integral x displaystyle x ve y displaystyle y tarafindan sinirlanir Bu nedenle bu durum logaritmik ortalama icin de gecerli olur Ayrica integral isleminin ortalama islemine aktarilir Buradan hareketle L cx cy cL x y displaystyle L cx cy cL x y esitliginin gecerli oldugu kolayca gorulebilir Logaritmik ortalamanin diger iki faydali integral gosterimi 1L x y 01dttx 1 t y displaystyle 1 over L x y int 0 1 operatorname d t over tx 1 t y ve 1L x y 0 dt t x t y displaystyle 1 over L x y int 0 infty operatorname d t over t x t y seklindedir Tanimin genellestirilmesiOrtalama deger teoremi yorumu Logaritmik ortalama goz onune alinarak dogal logaritma fonksiyonunun n displaystyle n turevi icin n 1 displaystyle n 1 degiskenli duruma genellestirilebilir ln x0 xn displaystyle ln left left x 0 dots x n right right ifadesi dogal logaritmanin gostermek uzere LMV x0 xn 1 n 1 nln x0 xn n displaystyle L text MV x 0 dots x n sqrt n 1 n 1 n ln left left x 0 dots x n right right Bu genellestirme n 2 displaystyle n 2 durumunda asagidaki tanimi ortaya cikarir LMV x y z x y y z z x 2 y z ln x z x ln y x y ln z displaystyle L text MV x y z sqrt frac x y left y z right left z x right 2 left left y z right ln left x right left z x right ln left y right left x y right ln left z right right Integral yorumu Logaritmik ortalamanin integral yorumu da daha fazla degiskene genellestirilebilir ancak bu durum farkli bir sonuca yol acar S a0 an a0 an 1 a0 0 an 0 textstyle S left alpha 0 dots alpha n right left alpha 0 dots alpha n 1 right land left alpha 0 geq 0 right land dots land left alpha n geq 0 right biciminde tanimlanan bir ve bu simpleksin hacminin 1 birim olmasini saglayan bir da textstyle mathrm d alpha olcusu verildiginde asagidaki tanimi elde ederiz LI x0 xn Sx0a0 xnan da displaystyle L text I left x 0 dots x n right int S x 0 alpha 0 cdot cdots cdot x n alpha n mathrm d alpha Bu tanim ustel fonksiyonun bolunmus farklari kullanilarak asagidaki gibi basitlestirilebilir LI x0 xn n exp ln x0 ln xn displaystyle L text I left x 0 dots x n right n exp left ln left x 0 right dots ln left x n right right Diger ortalamalarla iliskisiSikca karsilasilan bazi ortalama cesitleri logaritmik ortalama cinsinden ifade edilebilir Aritmetik ortalama L x2 y2 L x y x y2 displaystyle frac L left x 2 y 2 right L x y frac x y 2 Geometrik ortalama L x y L 1x 1y xy displaystyle sqrt frac L left x y right L left frac 1 x frac 1 y right sqrt xy Harmonik ortalama L 1x 1y L 1x2 1y2 21x 1y displaystyle frac L left frac 1 x frac 1 y right L left frac 1 x 2 frac 1 y 2 right frac 2 frac 1 x frac 1 y Ayrica bakinizAritmetik ortalama Geometrik ortalama Harmonik ortalama Genellestirilmis ortalama Stolarsky ortalamasi en en Kaynaklar B C Carlson 1966 Some inequalities for hypergeometric functions Proc Amer Math Soc 17 32 39 doi 10 1090 s0002 9939 1966 0188497 6 B Ostle 1957 A comparison of two means Proc Montana Acad Sci 17 69 70 Tung Po Lin The Power Mean and the Logarithmic Mean The American Mathematical Monthly doi 10 1080 00029890 1974 11993684 Konuyla ilgili yayinlarStolarsky Kenneth 1975 Generalizations of the logarithmic mean 48 2 87 92 doi 10 2307 2689825 Dis baglantilarEric W Weisstein Arithmetic Logarithmic Geometric Mean Inequality MathWorld
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans












