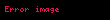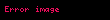Üs, bazen kuvvet, b taban, n üs veya kuvvet olmak üzere, bn olarak gösterilen ve "b üssü n", "b üzeri n" veya "b'nin n'inci kuvveti" olarak telaffuz edilen matematiksel işlem. Eğer n pozitif bir tam sayıysa, tabanın tekrarlanan çarpımına karşılık gelir:

Buna karşılık, sadece n pozitif bir tam sayı ise geçerlidir, çünkü bir şey -2 tane ya da tane vardır diyemeyiz. Üs yani n sayısının pozitif olmadığı durumlar aşağıda listelenmiştir.
İşlem
Kuvvet pozitif ise
23 işlemini ele alırsak, "2 üzeri 3" olarak okunan bu işlemin açılımı, 
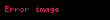

Kuvvet negatif ise
Bu durumda, üssün pozitif değeri alınır ve 1, taban üssü kuvvete bölünür:

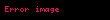
Kuvvet rasyonel bir sayı ise


Özellikler ve kurallar
- 1'in bütün kuvvetleri 1'dir.
- 0 dışındaki tüm sayıların 0. kuvveti: 1'dir.
- 0'ın 0 hariç bütün kuvvetleri 0'dır.
- Bir sayının 1. kuvveti, sayının kendisidir:
- Taban ve üs 0 ise o işlem belirsizdir.
(belirsiz)
- Pozitif sayıların bütün kuvvetleri daima pozitif bir sayı verir.
- Negatif sayılar parantez içinde ve kuvvetleri çift sayı ise sonuç pozitif olur, kuvvetleri tek sayı ise sonuç negatif olur:
(Kuvvet çift, taban parantezde.)
(Kuvvet çift, taban parantezde değil.)
(Kuvvet tek, daima negatif sonuç verir)
- Tabanları aynı iki üslü sayının çarpımı, taban üzeri kuvvetlerin toplamıdır:
- Tabanları aynı iki üslü sayının bölümü taban üzeri kuvvetlerin farkıdır:
Çarpmadan (üsler toplamından) farklı olarak, - Üslü bir sayının üssü alınırken, içteki kuvvet ile dıştaki kuvvet çarpılır:
- Üsler ortak parantezde dağılma özelliğine sahiptir:
- Üstler ve tabanlar aynı olacak şekilde,
-
ve
hariç, a ve b rasyonel sayı olmak üzere,
, başka bir değiş ile üs ile taban yer değiştirilirse sayının değeri de değişir.
-
(a ve b rasyonel sayı ise)
- a ve b 0'dan farklı tam sayılar olmak üzere,
Örnekler
(Bu soru ortaokul seviyesindedir.)
Çözüm:
sayısının yarısı kaçtır? (Bu soru ortaokul - lise seviyelerindedir.)
Çözüm:
ve
ise
(Bu soru lise seviyesindedir.)
Çözüm:
Sıralama
Üslü sayılarda sıralama yaparken ya tabanların ya da üslerin eşitlenmesi gerekir. Ondan sonra sıralama işlemi yapılır.
Örnekler
sayılarının küçükten büyüğe sırası nedir?
Çözüm:
3, 9 ve 27 sayıları 3'ün katı olduğu için, tabanlar 3 yapılabilir:
ve 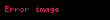
Küçükten büyüğe tabanlar aynı olduğu için, kuvvetlere bakarak sıralama yapılır:
sayılarının küçükten büyüğe sırası nedir?
Çözüm:
Üsler 18'de eşitlenebilir.
ve
Kuvvetlerin aynı olmasından ötürü, sıralama tabanlara göre yapılabilir: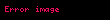
Basamak sayısı
Üslü sayıların basamak sayısını hesaplamak kolay değildir. Örneğin 


10'un n tane çarpımında, 1 yanına n adet sıfır gelecek şekilde düşünülerek, çıkan sayının kaç basamaklı olduğu bulunur, o halde:

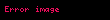

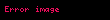
Örnekler
kaç basamaklıdır?
Çözüm:
- 252.82.3 işleminin sonucu kaç basamaklıdır?
Çözüm:
(52)2.(23)2.3
= 54.26.3
= 54.24.22.3
= 104.4.3 = 104.12 => 6 basamaklıdır.
Bilimsel gösterim
Çok büyük ya da çok küçük sayıların gösteriminde, hem gereken detayda sayının değerini, hem basamak sayısını veren hem de bunu daha okunabilir kolay bir şekilde yapan sayılsal gösterime bilimsel gösterim denir.
Gösterim


Özellikler ve Kurallar
- a sayısının 1 ile 10 arasında olması şarttır.
- Sayıda ',' yok ise, en sağdaki rakamın sonunda virgül varmış gibi düşünülmelidir.
ifadesi yok ise, bu, sayının yanında
olduğu anlamına gelir. Örneğin:
- Virgül sağa kaydıkça sayı büyür, 10'nun kuvveti de kayılan basamak sayısı kadar küçülür. Örneğin:
- Virgül sola kaydıkça sayı küçülür, 10'nun kuvveti de kayılan basamak sayısı kadar büyütülür. Örneğin:
Örnekler
- Işık saniyede 300000 km yol almaktadır. Buna göre ışığın 1 dakikada kaç km yol gittiğinin bilimsel gösterimi nedir?
Çözüm: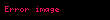
eşitliğini sağlayan x sayısının bilimsel gösterimi nedir?
Çözüm: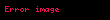
Reel üsler
Pozitif reel sayıların reel kuvvetleriyle üs alma, ya rasyonel kuvvetlerin süreklilikle reellere genişletilmesiyle ya da genelde olduğu gibi logaritma aracılığıyla üstel olarak ifade edilmesiyle tanımlanabilir. Sonuç her zaman pozitif bir reel sayıdır. Üsleri tam sayı olmayan pozitif reel tabanlar söz konusu olduğunda da, yukarıda pozitif tam sayı tabanlar için belirtilmiş özellikler ve kurallar aynı şekilde geçerlidir.
Öte yandan, negatif bir reel sayının reel kuvvetinin, reel olmayabileceğinden ve birden fazla değere sahip olabileceğinden dolayı, tutarlı bir şekilde tanımlanması çok daha zordur. Bu değerlerden biri, esas değer olarak seçilebilir, fakat aşağıdaki gibi özdeşlikler esas değerler için geçerli olmayabilir:

Bu nedenle, tabanı pozitif reel sayı olmayan bir üs alma işlemi genellikle kapsamında incelenir.
Ayrıca bakınız
- Logaritma ve Logaritma fonksiyonları
- Üstel fonksiyonlar
Kaynakça
- ^ "Compendium of Mathematical Symbols". Math Vault (İngilizce). 1 Mart 2020. 28 Nisan 2020 tarihinde kaynağından . Erişim tarihi: 27 Ağustos 2020.
- ^ a b Nykamp, Duane. "Basic rules for exponentiation". Math Insight. 1 Temmuz 2013 tarihinde kaynağından . Erişim tarihi: 27 Ağustos 2020.
- ^ a b Gangal, S. K. Gupta & Anubhuti. Composite Mathematics Book - 7 (İngilizce). S. Chand Publishing. ss. 78, 88. ISBN .
- ^ a b c d Mathematics for Senior High School Year X (İngilizce). Yudhistira Ghalia Indonesia. ss. 7-9. ISBN . 15 Şubat 2021 tarihinde kaynağından .
- ^ a b Yayınları, Eğitimiz (12 Aralık 2014). Temel Matematik: Sınava Hazırlık - Okula Yardımcı. Eğitimiz Yayınları. ss. 24,26. ISBN .
- ^ Choudhari. Modern School Mathematics Book - 6 (İngilizce). Orient Blackswan. s. 4. ISBN . 8 Şubat 2021 tarihinde kaynağından .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Us bazen kuvvet b taban n us veya kuvvet olmak uzere bn olarak gosterilen ve b ussu n b uzeri n veya b nin n inci kuvveti olarak telaffuz edilen matematiksel islem Eger n pozitif bir tam sayiysa tabanin tekrarlanan carpimina karsilik gelir Uslu sayilarin gosterimi taban ve kuvvet us bn b b nkere displaystyle b n underbrace b times dots times b n textrm kere Buna karsilik sadece n pozitif bir tam sayi ise gecerlidir cunku bir sey 2 tane ya da 12 displaystyle 1 over 2 tane vardir diyemeyiz Us yani n sayisinin pozitif olmadigi durumlar asagida listelenmistir IslemKuvvet pozitif ise 23 islemini ele alirsak 2 uzeri 3 olarak okunan bu islemin acilimi 23 2 2 2 3kere 8 displaystyle 2 3 underbrace 2 times 2 times 2 3 textrm kere 8 olacaktir Bu 3 tane 2 nin carpiminin sonucudur 34 displaystyle 3 4 isleminin acilimi ise 34 3 3 3 3 4kere 81 displaystyle 3 4 underbrace 3 times 3 times 3 times 3 4 textrm kere 81 olacaktir Bu ise 4 tane 3 un carpiminin sonucudur Kuvvet negatif ise Bu durumda ussun pozitif degeri alinir ve 1 taban ussu kuvvete bolunur a n 1an displaystyle a n 1 over a n 2 3 123 18 displaystyle 2 3 1 over 2 3 1 over 8 olur Kuvvet rasyonel bir sayi ise a12 displaystyle a 1 over 2 orneginde oldugu gibi us bir rasyonel sayi ise bu a displaystyle sqrt a olarak bir koklu sayi olusturur Bu konu icin koklu sayilar incelenebilinir Ozellikler ve kurallar1 in butun kuvvetleri 1 dir 1n 1 displaystyle 1 n 1 0 disindaki tum sayilarin 0 kuvveti 1 dir a 0 a0 1 displaystyle a neq 0 a 0 1 0 in 0 haric butun kuvvetleri 0 dir 0100 0 displaystyle 0 100 0 Bir sayinin 1 kuvveti sayinin kendisidir a1 a displaystyle a 1 a Taban ve us 0 ise o islem belirsizdir 00 displaystyle 0 0 belirsiz Pozitif sayilarin butun kuvvetleri daima pozitif bir sayi verir Negatif sayilar parantez icinde ve kuvvetleri cift sayi ise sonuc pozitif olur kuvvetleri tek sayi ise sonuc negatif olur 2 4 2 2 2 2 16 displaystyle 2 4 2 cdot 2 cdot 2 cdot 2 16 Kuvvet cift taban parantezde 24 2 2 2 2 16 displaystyle 2 4 2 cdot 2 cdot 2 cdot 2 16 Kuvvet cift taban parantezde degil 2 3 2 2 2 8 displaystyle 2 3 2 cdot 2 cdot 2 8 Kuvvet tek daima negatif sonuc verir 23 2 2 2 8 displaystyle 2 3 2 cdot 2 cdot 2 8 Tabanlari ayni iki uslu sayinin carpimi taban uzeri kuvvetlerin toplamidir am an a a mkere a a nkere am n displaystyle a m cdot a n underbrace a times dots times a m textrm kere times underbrace a times dots times a n textrm kere a m n Tabanlari ayni iki uslu sayinin bolumu taban uzeri kuvvetlerin farkidir aman am n displaystyle frac a m a n a m n Carpmadan usler toplamindan farkli olarak m n aman anam displaystyle m neq n implies frac a m a n neq frac a n a m Uslu bir sayinin ussu alinirken icteki kuvvet ile distaki kuvvet carpilir am n an m am n displaystyle a m n a n m a m cdot n Usler ortak parantezde dagilma ozelligine sahiptir anbn ab n displaystyle frac a n b n Big frac a b Big n Ustler ve tabanlar ayni olacak sekilde p an q an p q an displaystyle p cdot a n pm q cdot a n p pm q cdot a n 42 displaystyle 4 2 ve 24 displaystyle 2 4 haric a ve b rasyonel sayi olmak uzere a b ab ba displaystyle a neq b implies a b neq b a baska bir degis ile us ile taban yer degistirilirse sayinin degeri de degisir 3a 3b a b displaystyle 3 a 3 b Rightarrow a b a ve b rasyonel sayi ise a ve b 0 dan farkli tam sayilar olmak uzere ab n ba n displaystyle frac a b n frac b a n Ornekler 23 2 1 13 displaystyle frac 2 3 2 cdot 1 frac 1 3 Bu soru ortaokul seviyesindedir Cozum 32 2 23 94 23 32 11 32 displaystyle frac 3 2 2 cdot frac 2 3 frac 9 4 cdot frac 2 3 frac 3 2 cdot frac 1 1 frac 3 2 4 4 displaystyle 4 4 sayisinin yarisi kactir Bu soru ortaokul lise seviyelerindedir Cozum 22 42 2 82 2 8 1 2 9 displaystyle frac 2 2 4 2 frac 2 8 2 2 8 1 2 9 3x 3 52x y 5 displaystyle 3 x 3 5 2x y 5 ve x y Z displaystyle x y in mathbb Z ise x y displaystyle x cdot y Bu soru lise seviyesindedir Cozum x 3 0 x 3 displaystyle x 3 0 implies x 3 2x y 5 0 2 3 y 5 0 6 5 y y 1 displaystyle 2x y 5 0 implies 2 cdot 3 y 5 0 implies 6 5 y implies y 1 x y 3 1 3 displaystyle x cdot y 3 cdot 1 3 SiralamaUslu sayilarda siralama yaparken ya tabanlarin ya da uslerin esitlenmesi gerekir Ondan sonra siralama islemi yapilir Ornekler 34 98 271 displaystyle 3 4 9 8 27 1 sayilarinin kucukten buyuge sirasi nedir Cozum 3 9 ve 27 sayilari 3 un kati oldugu icin tabanlar 3 yapilabilir 98 32 8 316 displaystyle 9 8 3 2 8 3 16 271 33 1 33 displaystyle 27 1 3 3 1 3 3 ve 34 displaystyle 3 4 olur Kucukten buyuge tabanlar ayni oldugu icin kuvvetlere bakarak siralama yapilir 33 lt 34 lt 316 271 lt 34 lt 98 displaystyle 3 3 lt 3 4 lt 3 16 implies 27 1 lt 3 4 lt 9 8 218 99 1256 displaystyle 2 18 9 9 125 6 sayilarinin kucukten buyuge sirasi nedir Cozum Usler 18 de esitlenebilir 99 32 9 318 displaystyle 9 9 3 2 9 3 18 1256 53 6 518 displaystyle 125 6 5 3 6 5 18 ve 218 displaystyle 2 18 Kuvvetlerin ayni olmasindan oturu siralama tabanlara gore yapilabilir 218 lt 318 lt 518 218 lt 99 lt 1256 displaystyle 2 18 lt 3 18 lt 5 18 implies 2 18 lt 9 9 lt 125 6 Basamak sayisiUslu sayilarin basamak sayisini hesaplamak kolay degildir Ornegin 2195 displaystyle 2 195 sayisinin basamak sayisini bakarak bulamayiz 195 tane 2 nin carpimini bulup kac basamakli oldugu hesaplanabilir Bu yuzden genelde tabani 10 olan uslu sayilarin basamak sayisini bulmaya yonelmek gerekir ornegin 103 10 10 10 1000 displaystyle 10 3 10 cdot 10 cdot 10 1000 1 in yaninda 3 sifir 105 10 10 10 10 10 100 000 displaystyle 10 5 10 cdot 10 cdot 10 cdot 10 cdot 10 100 000 1 in yaninda 5 sifir 10 un n tane carpiminda 1 yanina n adet sifir gelecek sekilde dusunulerek cikan sayinin kac basamakli oldugu bulunur o halde 107 displaystyle 10 7 implies 1 in yaninda 7 sifir displaystyle implies 8 basamakli bir sayi 1020 displaystyle 10 20 implies 1 in yaninda 20 sifir displaystyle implies 21 basamakli bir sayi Ornekler 53 1050 displaystyle 5 3 cdot 10 50 kac basamaklidir Cozum 53 1050 125 1050 displaystyle 5 3 cdot 10 50 125 cdot 10 50 implies 125 3 basamak sayisinin yanina 50 sifir gelecek o halde 53 basamakli bir sayidir 252 82 3 isleminin sonucu kac basamaklidir Cozum 52 2 23 2 3 54 26 3 54 24 22 3 104 4 3 104 12 gt 6 basamaklidir Bilimsel gosterimCok buyuk ya da cok kucuk sayilarin gosteriminde hem gereken detayda sayinin degerini hem basamak sayisini veren hem de bunu daha okunabilir kolay bir sekilde yapan sayilsal gosterime bilimsel gosterim denir Gosterim 1 a lt 10 displaystyle 1 leq a lt 10 ve n bir tam sayi olmak uzere bilimsel gosterim a 10n displaystyle a cdot 10 n olarak yazilir Ozellikler ve Kurallar a sayisinin 1 ile 10 arasinda olmasi sarttir Sayida yok ise en sagdaki rakamin sonunda virgul varmis gibi dusunulmelidir 10n displaystyle 10 n ifadesi yok ise bu sayinin yaninda 100 displaystyle 10 0 oldugu anlamina gelir Ornegin 5 5 100 displaystyle 5 5 cdot 10 0 Virgul saga kaydikca sayi buyur 10 nun kuvveti de kayilan basamak sayisi kadar kuculur Ornegin 0 147 102 1 47 101 displaystyle 0 147 cdot 10 2 1 47 cdot 10 1 Virgul sola kaydikca sayi kuculur 10 nun kuvveti de kayilan basamak sayisi kadar buyutulur Ornegin 23 8 104 2 38 105 displaystyle 23 8 cdot 10 4 2 38 cdot 10 5 Ornekler Isik saniyede 300000 km yol almaktadir Buna gore isigin 1 dakikada kac km yol gittiginin bilimsel gosterimi nedir Cozum 1sn 300000km displaystyle 1sn rightarrow 300000km 60 300000 18 106 1 8 107km displaystyle 60 cdot 300000 18 cdot 10 6 1 8 cdot 10 7 km 0 0025 10 6 x 10 8 displaystyle 0 0025 cdot 10 6 x cdot 10 8 esitligini saglayan x sayisinin bilimsel gosterimi nedir Cozum 25 10 4 10 6 25 10 10 displaystyle 25 cdot 10 4 cdot 10 6 25 cdot 10 10 25 10 10 x 10 8 displaystyle 25 cdot 10 10 x cdot 10 8 x 25 10 1010 8 25 10 10 8 25 10 2 displaystyle x frac 25 cdot 10 10 10 8 25 cdot 10 10 8 25 cdot 10 2 x 2 5 10 1 displaystyle x 2 5 cdot 10 1 Reel uslerPozitif reel sayilarin reel kuvvetleriyle us alma ya rasyonel kuvvetlerin sureklilikle reellere genisletilmesiyle ya da genelde oldugu gibi logaritma araciligiyla ustel olarak ifade edilmesiyle tanimlanabilir Sonuc her zaman pozitif bir reel sayidir Usleri tam sayi olmayan pozitif reel tabanlar soz konusu oldugunda da yukarida pozitif tam sayi tabanlar icin belirtilmis ozellikler ve kurallar ayni sekilde gecerlidir Ote yandan negatif bir reel sayinin reel kuvvetinin reel olmayabileceginden ve birden fazla degere sahip olabileceginden dolayi tutarli bir sekilde tanimlanmasi cok daha zordur Bu degerlerden biri esas deger olarak secilebilir fakat asagidaki gibi ozdeslikler esas degerler icin gecerli olmayabilir br s br s displaystyle b r s b r s Bu nedenle tabani pozitif reel sayi olmayan bir us alma islemi genellikle kapsaminda incelenir Ayrica bakinizLogaritma ve Logaritma fonksiyonlari Ustel fonksiyonlarKaynakca Compendium of Mathematical Symbols Math Vault Ingilizce 1 Mart 2020 28 Nisan 2020 tarihinde kaynagindan Erisim tarihi 27 Agustos 2020 a b Nykamp Duane Basic rules for exponentiation Math Insight 1 Temmuz 2013 tarihinde kaynagindan Erisim tarihi 27 Agustos 2020 a b Gangal S K Gupta amp Anubhuti Composite Mathematics Book 7 Ingilizce S Chand Publishing ss 78 88 ISBN 978 81 219 2742 0 a b c d Mathematics for Senior High School Year X Ingilizce Yudhistira Ghalia Indonesia ss 7 9 ISBN 978 979 019 361 1 15 Subat 2021 tarihinde kaynagindan a b Yayinlari Egitimiz 12 Aralik 2014 Temel Matematik Sinava Hazirlik Okula Yardimci Egitimiz Yayinlari ss 24 26 ISBN 978 605 84701 0 1 Choudhari Modern School Mathematics Book 6 Ingilizce Orient Blackswan s 4 ISBN 978 81 7370 120 7 8 Subat 2021 tarihinde kaynagindan
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans