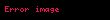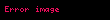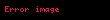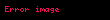Matematikte bir alt dalı olan diferansiyel geometride Bochner formülü bir üzerinde tanımlı harmonik fonksiyonları ilişkilendiren bir ifadedir. Bu ifade Galiçya doğumlu Amerikalı matematikçi Salomon Bochner'in adını taşımaktadır.
Formülün ifadesi
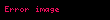
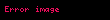
,
fonksiyonun
'ye göre gradyanı
,
fonksiyonun
'ye göre Hesse matrisi
ise
olsun. O zaman,
olur. Bunlara ek olarak, eğer 



haline dönüşür. Bochner bu formülü kullanarak ispatlamıştır.
Eğer 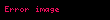
elde edilir. Gerçekten de, yukarıdaki formülün sol tarafı diverjans teoremi işe sıfır olur. Sağ taraftaki ilk ifadede de kısmi integral alma yöntemleri kullanılırsa sonuç elde edilir.
Ayrıca bakınız
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte bir alt dali olan diferansiyel geometride Bochner formulu bir uzerinde tanimli harmonik fonksiyonlari iliskilendiren bir ifadedir Bu ifade Galicya dogumlu Amerikali matematikci Salomon Bochner in adini tasimaktadir Formulun ifadesi M g displaystyle M g Riemann manifoldu olsun ve u M R displaystyle u colon M rightarrow mathbb R ise sonsuz turevlenebilir bir fonksiyon olsun u displaystyle nabla u u displaystyle u fonksiyonun g displaystyle g ye gore gradyani 2u displaystyle nabla 2 u u displaystyle u fonksiyonun g displaystyle g ye gore Hesse matrisi Ric displaystyle mbox Ric ise olsun O zaman 12D u 2 g Du u 2u 2 Ric u u displaystyle tfrac 1 2 Delta nabla u 2 g nabla Delta u nabla u nabla 2 u 2 mbox Ric nabla u nabla u olur Bunlara ek olarak eger u displaystyle u harmonikse yani D Dg displaystyle Delta Delta g g displaystyle g metrigine gore olmak uzere Du 0 displaystyle Delta u 0 ise Bochner formulu 12D u 2 2u 2 Ric u u displaystyle tfrac 1 2 Delta nabla u 2 nabla 2 u 2 mbox Ric nabla u nabla u haline donusur Bochner bu formulu kullanarak ispatlamistir Eger M g displaystyle M g siniri olmayan bir Riemann manifoldu ve u M R displaystyle u colon M rightarrow mathbb R sonsuz turevlenebilir tikiz destekli bir fonksiyonsa o zaman Bochner formulunun sonucu olarak M Du 2dvol M 2u 2 Ric u u dvol displaystyle int M Delta u 2 d mbox vol int M Big nabla 2 u 2 mbox Ric nabla u nabla u Big d mbox vol elde edilir Gercekten de yukaridaki formulun sol tarafi diverjans teoremi ise sifir olur Sag taraftaki ilk ifadede de kismi integral alma yontemleri kullanilirsa sonuc elde edilir Ayrica bakinizBochner ozdesligiKaynakca Chow Bennett Lu Peng Ni Lei 2006 Hamilton s Ricci flow 77 Providence RI Science Press New York s 19 ISBN 978 0 8218 4231 7 MR 2274812
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State