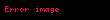Türev, diğer sayı kümeleri üzerindeki fonksiyonlar için de genellenmiş olmasına rağmen öncelikle reel değerli, yani reel sayılardan reel sayılara giden tek değişkenli fonksiyonlar için tanımlanmış, herhangi bir teğetin herhangi bir eğriye x ekseniyle yaptığı pozitif yönlü açının tanjant değeridir.

Birinci tanımı (h türevi)

Bu türden bir f fonksiyonunun a noktasındaki türevin
=
![image]()
Türevin geometrik tarifi
limiti olarak tanımlanır. Bu limit eğer var ise, yani bir reel sayıysa, f fonksiyonu a noktasında türevlenebilirdir denir. Limitin sonsuz olması veya var olmaması durumunda, f'ye a noktasında türevlenemez denir. Bu limitin temsil ettiği oran yukarıdaki grafikte gösterilmiştir. Limiti alınan oran, yani 
Yukarıdaki grafikte h değeri sıfıra yaklaştıkça, d doğrusu da y = f(a) eğrisine (a, f(a)) noktasındaki teğete yaklaşır. Burada :



Yukarıdaki limit a civarında doğrudur. Başka bir deyişle h sayısı 0 civarında 0'a yaklaştıkça a + h sayısı a civarında a'ya yaklaşır. Bu sebepten dolayı eğer uç noktalarda türev alınacaksa, limit sembolü soldan limit veya sağdan limit olarak yazılmalıdır. Analiz kitapları, genellikle sürekli fonksiyonları kapalı aralıklarda, türevlenebilir fonksiyonları ise açık aralıklarda tanımladıklarından sol ve sağ limit tanımlamazlar.
İkinci tanımı (q türevi)
Türevin birinci tanımını örnekleyerek bir ikinci tanım daha yapılabilir.
ifadesinin mantığında {h} sonsuz küçüğünü ekleme işlemi yapılmıştır. Genelleştirilmiş şekliyle sonsuz küçük artırımı yerine sonsuz küçük katının artırımı da yapılabilir.
Bir f(x) fonksiyonunu q türevi
sıklıkla 
=
ayrıca;
=
elde edilebilir.
Yönlü türev
Eğer f bir Rn üzerinde gerçek değerli fonksiyon ise yönü içinde f in kısmî türevi içinde çeşitli ölçmeler ise (mesela f bir x ve y fonksiyonunun x yönü ve y yönü içinde f 'nin kısmî türevinde çeşitli ölçmeler ise) buna yönlü türev denir.
Bununla birlikte köşegen çizgi y = x boyunca gibi herhangi diğer yön içinde f in yönlü ölçü çeşitleri yoktur.
Burada yönlü türev ölçüsü kullanılıyor.
bir vektörse vnin yönü içinde fin yönlü türevinin x noktasında sınırıdır.
Bâzı durumlarda bu vektörün uzunluğunu değiştirme sonrası yön türevi hesaplamak veya tahmin etmek daha kolay olabilir. Genellikle bu bir birim vektör yönünde bir yönde türevinin hesaplanması içinde sorunu açmak için yapılır. Bunun nasıl çalıştığını görmek için bunu v = λu varsayalım.h = k/λ fark katsayısı içinde yerine konur.Aradaki fark katsayısı:
Bu u sırasıyla fin yönlü türevi için λ zaman içinde farklı katsayısıdır. Dahası sıfıra yönelen k olarak alınan limit olarak aynı h ve k için herhangi diğerinin çarpımıdır. Bunun için Dv(f) = λDu(f). Bu nedenle yeniden ölçeklendirme özelliği, yönlü türevler sık sık sadece birim vektörler için kabul edilir.
Eğer f'in tüm kısmî türevleri var ve x'de sürekli ve formülü ile v yönünde f içinde belirlenen yönlü türev ise
Bu tanımının bir sonucudur. Bu yönlü türev, aşağıda v içinde . Bu da
Dv + w(f) = Dv(f) + Dw(f).
demektir. Aynı tanım, ayrıca f olduğunda Rm içindeki değerleri ile bir fonksiyondur. Yukardaki tanım, vektörlerin her bir bileşeni için uygulanır. Bu durum içinde yönlü türev Rm içinde bir vektördür.

 (mavi eğri) için yarı türev (mor eğri) ve birinci türev (kırmızı eğri).
(mavi eğri) için yarı türev (mor eğri) ve birinci türev (kırmızı eğri).tek terimli olduğunu varsayalım
.
Burada kullanılan türev
tekrarlanarak şu sonuca ulaşılır:
faktöriyel yerine Gama fonksiyonu alınırsa
x'in yarı türevi
Bu durumu tekrarlarsak
Gerçekten burada beklenen sonuç aynıdır.
Buradaki türev alma işlemi sadece reel sayılarla sınırlı değildir. Mesela (1 + i)inci türev, (1 - i)inci türev iki türevlidir. Ancak negatif değerler için alınan a, integrali verir.
Laplace dönüşümü
Laplace dönüşümünün ifadesi
ve
v.s. Beklentimiz
.
Mesela
beklentisi doğrudur. Gerçekten verilen konvolüsyon kök 

verir. bâzı fonksiyonların kullanılabilmesi ile ilişkilidir. Sıklıkla kesirli diferansiyel denklemler çözümünde kullanılır.
Kısmî türev
Kısmî türev, çok değişkenli bir fonksiyonun sadece ilgili değişkeni sabit değilken alınan türevdir. Bu tarz türevleri içeren denklemlere kısmî diferansiyel denklem denir.
Kısmî türevin tanımı

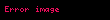
şeklinde tanımlanan n tane bağımsız değişkene bağlı z fonksiyonunun diğer değişkenler sabit tutularak herhangi bir değişkendeki 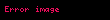
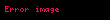

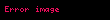
ifadesine 
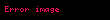

şeklinde gösterilir.



Örnek:

Ayrıca q türevinin tanımına uygun olarak kısmî türev içinde kesirli kısmî türev tanımı yapılabilir.
Türev alma
Fonksiyonlar, en genel biçimde cebirsel, trigonometrik üstel veya logaritmik olarak üçe ayrılırlar. Bu ayrımın kombinasyonları da olabilir. Her üç genel şeklin türev alma biçimleri farklılık gösterir. Ama türevin tanımının mantığı değişmez, yani türevlenebilir bir f fonksiyonu için her a noktasındaki değeri f fonksiyonun a noktasındaki türevi olan fonksiyona f fonksiyonun türevi denir ve bu fonksiyon f' sembolüyle gösterilir. Ayrıca
formülü, f'nin türevlenebildiği her 
Örnekler
Türevlenebilir fonksiyonlar ve türevleri
Cebirsel
- Herhangi bir sıfırdan farklı n reel sayısı için
fonksiyonu,
Bu eşitlik Binom Teoremi'nin bir sonucudur. (Bu formül yalnızca reel sayılarda kullanılır!)
Trigonometrik
- sin(x) ve cos(x) trigonometrik fonksiyonları,
Üstel veya logaritmik
üstel fonksiyonu,
logaritmik fonksiyonu,
Türevlenemeyen fonksiyonlar
- Mutlak değer fonksiyonu 0 noktasında türevli değildir. Nedeni, 0'da türevi tanımlayan
limitinin bulunamamasıdır. Diğer her noktada türevlidir.
fonksiyonu da 0'da türevli olmayıp da başka her yerde türevli olan bir fonksiyondur. Bu fonksiyonun 0'da türevlenebilir olmayışının nedeni
limitinin 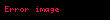

Temel teoremler
Çok karmaşık görünümlü fonksiyonların da türevlerini almamızı kolaylaştıracak teknikler (teoremler) mevcuttur.
- (f ± g)'(a) = f'(a) ± g'(a),
- (f × g)'(a) = f'(a) × g(a) + g'(a) × f(a) (Çarpım Kuralı olarak bilinir),
- (f o g)'(a) = f'(g(a)) × g'(a) (Bileşke fonksiyonun türevi, zincir kuralı olarak bilinir).
- (f / g)'(a) = [f'(a) × g(a) - g'(a) × f(a)] / g²(a) (Fark Kuralı).
Genellemeler
- Türev alma operasyonunu birden çok kez uygulamak mümkündür. Eğer f' , f fonksiyonunun türeviyse ve de f", f' fonksiyonunun türeviyse o zaman f" fonksiyonuna f fonksiyonunun ikinci türevi denir. Daha yüksek dereceden türevler de benzer şekilde tanımlanır.
- Türevi alınan f fonksiyonunun reel değerli olması şart değildir. Mesela f kompleks sayılar veya p-sel sayılar üzerinde tanımlı bir fonksiyon olabileceği gibi aldığı değerleri de reel sayılar dışındaki uygun bir kümeden (kompleks sayılar kümesi gibi) alıyor olabilir.
- Tek değişkenli olmayan fonksiyonların da türevlerinden bahsetmek mümkündür. Ancak önce yukardaki limitli tanımı ve teğet doğrusu argümanını bu duruma uyarlamak gereklidir. Bu konu, maddesinde bulunur.
Türevin uygulamaları
- f fonksiyonunun a noktasında türevi, f'nin grafiğine a noktasında çizilen teğetin eğimini verdiğinden bir fonksiyonun birinci ve ikinci türevlerine bakarak o fonksiyonun grafiğinin davranışları hakkında grafiği kaba taslak çizmemize yetecek kadar bilgi edinmemiz mümkündür.
- Hesabın temel teoremi'ne göre türev almakla integral almak, birbirlerinin tersi olan iki operasyondur.
- Taylor açılımları, bir fonksiyonun bir noktadaki ilk birkaç dereceden türevini kullanarak o fonksiyona yakın bir ifadeli fonksiyon bulmamıza yararlar. Çoğu zaman polinom ifadeli olmayan bir fonksiyonun bir noktadaki tam değerini bulmak sonsuz sayıda işlem gerektirdiğinden buna karşılık polinom değerli fonksiyonların değerini hesaplamak sonlu bir işlem olduğundan bu açılımlar ve türev kavramı vazgeçilmezdir.
- Yaygın doğa felsefesi görüşüne göre, doğada gerçekleşen fiziksel olayların tümü sürekli yumuşak geçişlidir. Tıpkı buzluktan çıkardığımız bir buzun aniden değil de yavaş yavaş erimesinde olduğu gibi. Dolayısıyla fiziksel olayları tarif etmekte kullanılan fonksiyonların hemen hepsinin türevlenebilir olması beklenir. Matematiğin diferansiyel denklemler dalı, doğada gözlenen verilerden bu tür fonksiyonlar çıkartma yöntemleri bulmak amacıyla geliştirilmiştir.
- Matematiğin diferansiyel geometri ve diferansiyel topoloji alanları öncelikle türevlenebilir fonksiyonlar aracılığıyla tarif edilebilen geometrik yapılarla ilgilenirler.
Çarpım ve bölüm fonksiyonlarının türevi
- Çarpım fonksiyonunun türevi:


İspat:













- Bölüm fonksiyonunun türevi:


İspat:














wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Turev diger sayi kumeleri uzerindeki fonksiyonlar icin de genellenmis olmasina ragmen oncelikle reel degerli yani reel sayilardan reel sayilara giden tek degiskenli fonksiyonlar icin tanimlanmis herhangi bir tegetin herhangi bir egriye x ekseniyle yaptigi pozitif yonlu acinin tanjant degeridir Fonksiyonun grafigi siyah teget gecen dogrunun grafigi kirmizi renkte gosterilmistir Teget cizginin egimi fonksiyonun turevine esittir Birinci tanimi h turevi Turevin sezgisel fikrini veren animasyon argumanin degismesiyle fonksiyonun salinimi degisir Bu turden bir f fonksiyonunun a noktasindaki turevin limh 0f a h f a a h a displaystyle lim h rightarrow 0 frac f a h f a a h a limh 0f a h f a h displaystyle lim h rightarrow 0 frac f a h f a h Turevin geometrik tarifi limiti olarak tanimlanir Bu limit eger var ise yani bir reel sayiysa f fonksiyonu a noktasinda turevlenebilirdir denir Limitin sonsuz olmasi veya var olmamasi durumunda f ye a noktasinda turevlenemez denir Bu limitin temsil ettigi oran yukaridaki grafikte gosterilmistir Limiti alinan oran yani f a h f a h displaystyle frac f a h f a h orani olarak adlandirilir Yukaridaki grafikte h degeri sifira yaklastikca d dogrusu da y f a egrisine a f a noktasindaki tegete yaklasir Burada f a h f a h displaystyle frac f a h f a h ifadesinin de d dogrusunun egimini verdigine dikkat etmek gerekir a displaystyle a noktasinda turevlenebilen bir fonksiyon a displaystyle a civarinda surekli olmak zorundadir Fakat bunun tersi dogru degildir Baska bir ifadeyle a displaystyle a civarinda surekli olan fakat turevlenemeyen fonksiyon bulmak mumkundur Ornek olarak Weierstrass fonksiyonu reel sayilar kumesinin her noktasinda surekli olmasina karsin hicbir noktasinda turevlenebilir degildir Yukaridaki limit a civarinda dogrudur Baska bir deyisle h sayisi 0 civarinda 0 a yaklastikca a h sayisi a civarinda a ya yaklasir Bu sebepten dolayi eger uc noktalarda turev alinacaksa limit sembolu soldan limit veya sagdan limit olarak yazilmalidir Analiz kitaplari genellikle surekli fonksiyonlari kapali araliklarda turevlenebilir fonksiyonlari ise acik araliklarda tanimladiklarindan sol ve sag limit tanimlamazlar Ikinci tanimi q turevi Turevin birinci tanimini ornekleyerek bir ikinci tanim daha yapilabilir f a h f a h displaystyle frac f a h f a h ifadesinin mantiginda h sonsuz kucugunu ekleme islemi yapilmistir Genellestirilmis sekliyle sonsuz kucuk artirimi yerine sonsuz kucuk katinin artirimi da yapilabilir Bir f x fonksiyonunu q turevi ddx qf x f qx f x qx x displaystyle left frac d dx right q f x frac f qx f x qx x siklikla Dqf x displaystyle D q f x seklinde yazilir q turev olarak bilinir limh 1f ah f a ah a displaystyle lim h rightarrow 1 frac f a h f a a h a limh 0f a h f a h displaystyle lim h rightarrow 0 frac f a h f a h limh 1f ah f a ah a displaystyle lim h rightarrow 1 frac f a h f a a h a ayrica df a da f a displaystyle frac df a da f a limh 1f ah f a a h 1 displaystyle lim h rightarrow 1 frac f a h f a a h 1 elde edilebilir Yonlu turevEger f bir Rn uzerinde gercek degerli fonksiyon ise yonu icinde f in kismi turevi icinde cesitli olcmeler ise mesela f bir x ve y fonksiyonunun x yonu ve y yonu icinde f nin kismi turevinde cesitli olcmeler ise buna yonlu turev denir Bununla birlikte kosegen cizgi y x boyunca gibi herhangi diger yon icinde f in yonlu olcu cesitleri yoktur Burada yonlu turev olcusu kullaniliyor v v1 vn displaystyle mathbf v v 1 ldots v n bir vektorse vnin yonu icinde fin yonlu turevinin x noktasinda siniridir Dvf x limh 0f x hv f x h displaystyle mathrm D mathbf v f mathbf x lim h rightarrow 0 frac f mathbf x h mathbf v f mathbf x h Bazi durumlarda bu vektorun uzunlugunu degistirme sonrasi yon turevi hesaplamak veya tahmin etmek daha kolay olabilir Genellikle bu bir birim vektor yonunde bir yonde turevinin hesaplanmasi icinde sorunu acmak icin yapilir Bunun nasil calistigini gormek icin bunu v lu varsayalim h k l fark katsayisi icinde yerine konur Aradaki fark katsayisi f x k l lu f x k l l f x ku f x k displaystyle frac f mathbf x k lambda lambda mathbf u f mathbf x k lambda lambda cdot frac f mathbf x k mathbf u f mathbf x k Bu u sirasiyla fin yonlu turevi icin l zaman icinde farkli katsayisidir Dahasi sifira yonelen k olarak alinan limit olarak ayni h ve k icin herhangi digerinin carpimidir Bunun icin Dv f lDu f Bu nedenle yeniden olceklendirme ozelligi yonlu turevler sik sik sadece birim vektorler icin kabul edilir Eger f in tum kismi turevleri var ve x de surekli ve formulu ile v yonunde f icinde belirlenen yonlu turev ise Dvf x j 1nvj f xj displaystyle mathrm D mathbf v f boldsymbol x sum j 1 n v j frac partial f partial x j Bu taniminin bir sonucudur Bu yonlu turev asagida v icinde Bu da Dv w f Dv f Dw f demektir Ayni tanim ayrica f oldugunda Rm icindeki degerleri ile bir fonksiyondur Yukardaki tanim vektorlerin her bir bileseni icin uygulanir Bu durum icinde yonlu turev Rm icinde bir vektordur Kesirli turevfonksiyon f x x displaystyle f x x mavi egri icin yari turev mor egri ve birinci turev kirmizi egri f x displaystyle f x tek terimli oldugunu varsayalimf x xk displaystyle f x x k dd Burada kullanilan turev f x ddxf x kxk 1 displaystyle f x d over dx f x kx k 1 dd tekrarlanarak su sonuca ulasilir dadxaxk k k a xk a displaystyle d a over dx a x k k over k a x k a dd faktoriyel yerine Gama fonksiyonu alinirsa dadxaxk G k 1 G k a 1 xk a displaystyle d a over dx a x k Gamma k 1 over Gamma k a 1 x k a dd x in yari turevi d12dx12x G 1 1 G 1 12 1 x1 12 G 2 G 32 x12 2p 12x12 2x12p displaystyle d 1 over 2 over dx 1 over 2 x Gamma 1 1 over Gamma 1 1 over 2 1 x 1 1 over 2 Gamma 2 over Gamma 3 over 2 x 1 over 2 2 pi 1 over 2 x 1 over 2 frac 2 x 1 over 2 sqrt pi dd Bu durumu tekrarlarsak d12dx122p 12x12 2p 12G 1 12 G 12 12 1 x12 12 2p 12G 32 G 1 x0 1G 1 1 displaystyle d 1 over 2 over dx 1 over 2 2 pi 1 over 2 x 1 over 2 2 pi 1 over 2 Gamma 1 1 over 2 over Gamma 1 over 2 1 over 2 1 x 1 over 2 1 over 2 2 pi 1 over 2 Gamma 3 over 2 over Gamma 1 x 0 1 over Gamma 1 1 dd Gercekten burada beklenen sonuc aynidir d1 2dx1 2d1 2dx1 2 x ddxx 1 displaystyle left frac d 1 2 dx 1 2 frac d 1 2 dx 1 2 right x d over dx x 1 dd Buradaki turev alma islemi sadece reel sayilarla sinirli degildir Mesela 1 i inci turev 1 i inci turev iki turevlidir Ancak negatif degerler icin alinan a integrali verir Laplace donusumu Laplace donusumunun ifadesi L Jf s L 0tf t dt s 1s L f s displaystyle mathcal L left Jf right s mathcal L left int 0 t f tau d tau right s frac 1 s mathcal L left f right s ve L J2f 1s L Jf s 1s2 L f s displaystyle mathcal L left J 2 f right frac 1 s mathcal L left Jf right s frac 1 s 2 mathcal L left f right s v s Beklentimiz Jaf L 1 s a L f s displaystyle J alpha f mathcal L 1 left s alpha mathcal L f s right Mesela Ja tk L 1 G k 1 sa k 1 G k 1 G a k 1 ta k displaystyle begin array lcr J alpha left t k right amp amp mathcal L 1 left dfrac Gamma k 1 s alpha k 1 right amp amp dfrac Gamma k 1 Gamma alpha k 1 t alpha k end array beklentisi dogrudur Gercekten verilen konvolusyon kok L f g L f L g displaystyle mathcal L f g mathcal L f mathcal L g ve kisaca p x xa 1 displaystyle p x x alpha 1 dogrulama icin bulunur Jaf t 1G a L 1 L p L f 1G a p f 1G a 0tp t t f t dt 1G a 0t t t a 1f t dt displaystyle begin array rcl J alpha f t amp amp frac 1 Gamma alpha mathcal L 1 left left mathcal L p right mathcal L f right amp amp frac 1 Gamma alpha p f amp amp frac 1 Gamma alpha int 0 t p t tau f tau d tau amp amp frac 1 Gamma alpha int 0 t t tau alpha 1 f tau d tau end array verir bazi fonksiyonlarin kullanilabilmesi ile iliskilidir Siklikla kesirli diferansiyel denklemler cozumunde kullanilir Kismi turevKismi turev cok degiskenli bir fonksiyonun sadece ilgili degiskeni sabit degilken alinan turevdir Bu tarz turevleri iceren denklemlere kismi diferansiyel denklem denir Kismi turevin tanimi z Rn Rn R displaystyle z mathbb R n times mathbb R n to mathbb R z f x1 x2 xm xn displaystyle z f x 1 x 2 x m x n seklinde tanimlanan n tane bagimsiz degiskene bagli z fonksiyonunun diger degiskenler sabit tutularak herhangi bir degiskendeki Dxm displaystyle Delta x m degisimine karsilik fonksiyonun degisim hizi DzDxm f x1 x2 xm Dxm xn f x1 x2 xm xn Dxm displaystyle frac Delta z Delta x m frac f x 1 x 2 x m Delta x m x n f x 1 x 2 x m x n Delta x m Dxm h displaystyle Delta x m h z xm limh 0f x1 x2 xm h xn f x1 x2 xm xn h displaystyle frac partial z partial x m underset h to 0 mathop lim frac f x 1 x 2 x m h x n f x 1 x 2 x m x n h ifadesine z displaystyle z fonksiyonunun xm displaystyle x m degiskenine gore kismi turevi denir f xm fxm Dxmf z xm zxm displaystyle frac partial f partial x m f x m D x m f frac partial z partial x m z x m seklinde gosterilir z f x y displaystyle z f left x y right ise fx x y limh 0f x h y f x y h displaystyle f x left x y right underset h to 0 mathop lim frac f left x h y right f left x y right h fy x y limk 0f x y k f x y k displaystyle f y left x y right underset k to 0 mathop lim frac f left x y k right f left x y right k Ornek f x y x3 x2y y3fx x3 x x2y x y3 xfx 3x2 2xy 0fx 3x2 2xy displaystyle begin aligned amp f x y x 3 x 2 y y 3 amp f x left x 3 right x left x 2 y right x left y 3 right x amp f x 3 x 2 2xy 0 amp f x 3 x 2 2xy end aligned Ayrica q turevinin tanimina uygun olarak kismi turev icinde kesirli kismi turev tanimi yapilabilir Turev almaFonksiyonlar en genel bicimde cebirsel trigonometrik ustel veya logaritmik olarak uce ayrilirlar Bu ayrimin kombinasyonlari da olabilir Her uc genel seklin turev alma bicimleri farklilik gosterir Ama turevin taniminin mantigi degismez yani turevlenebilir bir f fonksiyonu icin her a noktasindaki degeri f fonksiyonun a noktasindaki turevi olan fonksiyona f fonksiyonun turevi denir ve bu fonksiyon f semboluyle gosterilir Ayrica ddxf x f x displaystyle frac d dx f x f x formulu f nin turevlenebildigi her x displaystyle x te bu durumu ifade etmek icin kullanilir Burada f bir fonksiyon oldugundan f nun tanim kumesi f nin turevlenebildigi noktalarin kumesidir OrneklerTurevlenebilir fonksiyonlar ve turevleri Cebirsel Herhangi bir sifirdan farkli n reel sayisi icin f x xn displaystyle f x x n fonksiyonu ddxxn nxn 1 displaystyle frac d dx x n nx n 1 Bu esitlik Binom Teoremi nin bir sonucudur Bu formul yalnizca reel sayilarda kullanilir Trigonometrik sin x ve cos x trigonometrik fonksiyonlari ddxsin x cos x displaystyle frac d dx sin x cos x ddxcos x sin x displaystyle frac d dx cos x sin x Ustel veya logaritmik ex displaystyle e x ustel fonksiyonu ddxex ex displaystyle frac d dx e x e x xx displaystyle x x logaritmik fonksiyonu y xx displaystyle y x x y xx lnx 1 displaystyle y x x lnx 1 Turevlenemeyen fonksiyonlar Mutlak deger fonksiyonu 0 noktasinda turevli degildir Nedeni 0 da turevi tanimlayanlimh 0 0 h 0 h displaystyle lim h rightarrow 0 frac 0 h 0 h limitinin bulunamamasidir Diger her noktada turevlidir x3 displaystyle sqrt 3 x fonksiyonu da 0 da turevli olmayip da baska her yerde turevli olan bir fonksiyondur Bu fonksiyonun 0 da turevlenebilir olmayisinin nedenilimh 00 h3 03h displaystyle lim h rightarrow 0 frac sqrt 3 0 h sqrt 3 0 h limitinin displaystyle infty yani sonsuz olmasidir Dolayisiyla mutlak deger fonksiyonunun grafigi 0 noktasinda kirikken x3 displaystyle sqrt 3 x fonksiyonunun grafigi 0 da da kirilmasizdir Temel teoremlerCok karmasik gorunumlu fonksiyonlarin da turevlerini almamizi kolaylastiracak teknikler teoremler mevcuttur f g a f a g a f g a f a g a g a f a Carpim Kurali olarak bilinir f o g a f g a g a Bileske fonksiyonun turevi zincir kurali olarak bilinir f g a f a g a g a f a g a Fark Kurali GenellemelerTurev alma operasyonunu birden cok kez uygulamak mumkundur Eger f f fonksiyonunun tureviyse ve de f f fonksiyonunun tureviyse o zaman f fonksiyonuna f fonksiyonunun ikinci turevi denir Daha yuksek dereceden turevler de benzer sekilde tanimlanir Turevi alinan f fonksiyonunun reel degerli olmasi sart degildir Mesela f kompleks sayilar veya p sel sayilar uzerinde tanimli bir fonksiyon olabilecegi gibi aldigi degerleri de reel sayilar disindaki uygun bir kumeden kompleks sayilar kumesi gibi aliyor olabilir Tek degiskenli olmayan fonksiyonlarin da turevlerinden bahsetmek mumkundur Ancak once yukardaki limitli tanimi ve teget dogrusu argumanini bu duruma uyarlamak gereklidir Bu konu maddesinde bulunur Turevin uygulamalarif fonksiyonunun a noktasinda turevi f nin grafigine a noktasinda cizilen tegetin egimini verdiginden bir fonksiyonun birinci ve ikinci turevlerine bakarak o fonksiyonun grafiginin davranislari hakkinda grafigi kaba taslak cizmemize yetecek kadar bilgi edinmemiz mumkundur Hesabin temel teoremi ne gore turev almakla integral almak birbirlerinin tersi olan iki operasyondur Taylor acilimlari bir fonksiyonun bir noktadaki ilk birkac dereceden turevini kullanarak o fonksiyona yakin bir ifadeli fonksiyon bulmamiza yararlar Cogu zaman polinom ifadeli olmayan bir fonksiyonun bir noktadaki tam degerini bulmak sonsuz sayida islem gerektirdiginden buna karsilik polinom degerli fonksiyonlarin degerini hesaplamak sonlu bir islem oldugundan bu acilimlar ve turev kavrami vazgecilmezdir Yaygin doga felsefesi gorusune gore dogada gerceklesen fiziksel olaylarin tumu surekli yumusak gecislidir Tipki buzluktan cikardigimiz bir buzun aniden degil de yavas yavas erimesinde oldugu gibi Dolayisiyla fiziksel olaylari tarif etmekte kullanilan fonksiyonlarin hemen hepsinin turevlenebilir olmasi beklenir Matematigin diferansiyel denklemler dali dogada gozlenen verilerden bu tur fonksiyonlar cikartma yontemleri bulmak amaciyla gelistirilmistir Matematigin diferansiyel geometri ve diferansiyel topoloji alanlari oncelikle turevlenebilir fonksiyonlar araciligiyla tarif edilebilen geometrik yapilarla ilgilenirler Carpim ve bolum fonksiyonlarinin tureviCarpim fonksiyonunun turevi y f x g x displaystyle y f x g x olsun y f x g x g x f x displaystyle y f x g x g x f x dir Ispat y f x g x displaystyle y f x g x lny ln f x g x displaystyle lny ln f x g x lny lnf x lng x displaystyle lny lnf x lng x dlny d lnf x lng x displaystyle dlny d lnf x lng x dlny dlnf x dlng x displaystyle dlny dlnf x dlng x dyy df x f x dg x g x displaystyle frac dy y frac df x f x frac dg x g x dyy f x dxf x g x dxg x displaystyle frac dy y frac f x dx f x frac g x dx g x dyy f x g x dx g x f x dxf x g x displaystyle frac dy y frac f x g x dx g x f x dx f x g x dyf x g x f x g x dx g x f x dxf x g x displaystyle frac dy f x g x frac f x g x dx g x f x dx f x g x dy f x g x dx g x f x dx displaystyle dy f x g x dx g x f x dx dy dx f x g x g x f x displaystyle dy dx f x g x g x f x dydx f x g x g x f x displaystyle frac dy dx f x g x g x f x y f x g x g x f x displaystyle y f x g x g x f x Bolum fonksiyonunun turevi y f x g x displaystyle y frac f x g x olsun y f x g x g x f x g x 2 displaystyle y frac f x g x g x f x g x 2 dir Ispat y f x g x displaystyle y frac f x g x lny lnf x g x displaystyle lny ln frac f x g x lny lnf x lng x displaystyle lny lnf x lng x dlny d lnf x lng x displaystyle dlny d lnf x lng x dlny dlnf x dlng x displaystyle dlny dlnf x dlng x dyy df x f x dg x g x displaystyle frac dy y frac df x f x frac dg x g x dyy f x dxf x g x dxg x displaystyle frac dy y frac f x dx f x frac g x dx g x dyy f x g x dx g x f x dxf x g x displaystyle frac dy y frac f x g x dx g x f x dx f x g x dyf x g x f x g x dx g x f x dxf x g x displaystyle frac dy frac f x g x frac f x g x dx g x f x dx f x g x dy f x g x dx g x f x dx f x g x f x g x displaystyle dy frac f x g x dx g x f x dx f x g x frac f x g x dy f x g x dx g x f x dxg x 2 displaystyle dy frac f x g x dx g x f x dx g x 2 dy dx f x g x g x f x g x 2 displaystyle dy frac dx f x g x g x f x g x 2 dydx f x g x g x f x g x 2 displaystyle frac dy dx frac f x g x g x f x g x 2 y f x g x g x f x g x 2 displaystyle y frac f x g x g x f x g x 2
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans