Elektromanyetizmada ve optikte dağılma ya da dispersiyon, elektromanyetik dalganın ilerlediği ortamdaki faz hızının frekansına bağlı olması durumudur. Kırılma indisinin frekansa bağlılığı olarak da tanımlanabilmektedir. Bu özelliğe sahip ortamlar dağıtıcı ortamlar olarak bilinir. Faz hızı ile grup hızının eşit olması durumunda dağılma sıfırlanır; grup hızının daha büyük olması anormal dağılma olarak bilinir.İletim hatları ve optik fiberler gibi dalga kılavuzlarında dalga yayılımını büyük ölçüde etkileyen dağılma,dalga denkleminin geçerliği olduğu diğer sistemlerde de gözlemlenebilmektedir.

Bir sistemdeki sinyal iletimi dağılma diyagramı ile gösterilebilir; bu diyagram, frekans ile dalga vektörünü ilişkilendirir. Farklı frekansların farklı faz hızlarının olması ortam veya sistemde ilerleyen sinyallerde bozunmaya yol açar; düşük ve yüksek frekanslı bileşenler farklı hızda hareket ettiği için sinyal zarfı ilerleme ile birlikte genişler. Dalga kılavuzlarındaki dağılma, dalganın ilerlediği etken kırılma indisinin hesaplanması ile anlaşılabilir.
Kayıpsız iletim hatlarında dağılmasız iletim koşulları (telgrafçılar denklemleri) ile hesaplanabilmektedir.
Galeri
-
![image]() Bir ışık darbesinin dağılmalı bir ortamda bozunması
Bir ışık darbesinin dağılmalı bir ortamda bozunması -
![image]() Dağılma ile gök kuşağı oluşumu
Dağılma ile gök kuşağı oluşumu -
![image]() Bir kırınım ızgarasından geçen ampül ışığının dağılması
Bir kırınım ızgarasından geçen ampül ışığının dağılması
Yüksek dağılım mertebelerinin genelleştirilmiş formülasyonu -
Kromatik dağılımın Taylor katsayıları aracılığıyla pertürbatif bir şekilde tanımlanması, birkaç farklı sistemden gelen dağılımın dengelenmesi gereken optimizasyon problemleri için avantajlıdır. Örneğin, chirp pulse lazer amplifikatörlerinde, optik hasarı önlemek için pulslar önce bir gerici tarafından zaman içinde gerilir. Daha sonra amplifikasyon sürecinde, darbeler kaçınılmaz olarak malzemelerden geçen doğrusal ve doğrusal olmayan faz biriktirir. Ve son olarak, darbeler çeşitli tipte kompresörlerde sıkıştırılır. Biriken fazda kalan yüksek mertebeleri iptal etmek için genellikle tek tek mertebeler ölçülür ve dengelenir. Bununla birlikte, düzgün sistemler için, bu tür pertürbatif tanımlamaya genellikle ihtiyaç duyulmaz (örneğin, dalga kılavuzlarında yayılma). Dağılım düzenleri, Lah-Laguerre tipi dönüşümler şeklinde hesaplama dostu bir şekilde genelleştirilmiştir.
Dağılım mertebeleri, fazın veya dalga vektörünün Taylor açılımı ile tanımlanır.


Dalga vektörü 



Herhangi bir türevlenebilir fonksiyonun 



Dönüşümün matris elemanları Lah katsayılarıdır: 
GDD için yazılan yukarıdaki ifade, dalga boyu GGD olan bir sabitin sıfır yüksek mertebeye sahip olacağını belirtir. GDD'den değerlendirilen yüksek mertebeler şunlardır: 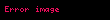
Kırılma indisi 


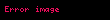


Dönüşümlerin matris elemanları eksi 2 mertebesindeki işaretsiz Laguerre katsayılarıdır ve şu şekilde verilir: 
Dalga vektörü için açıkça yazılan ilk on dağılım mertebesi şunlardır:

Grup kırılma indisi 




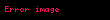





Açıkça, 









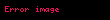



Ayrıca bakınız
| Wikimedia Commons'ta Dağılma ile ilgili ortam dosyaları bulunmaktadır. |
Kaynakça
- ^ Cheng 2015, s. 297.
- ^ Pozar 2014, s. 150.
- ^ Cheng 2015, s. 396.
- ^ Pedrotti, Pedrotti & Pedrotti 2006, ss. 253-260.
- ^ Pozar 2014, s. 49-56.
- ^ Popmintchev, Dimitar; Wang, Siyang; Xiaoshi, Zhang; Stoev, Ventzislav; Popmintchev, Tenio (24 Ekim 2022). "Analytical Lah-Laguerre optical formalism for perturbative chromatic dispersion". (İngilizce). 30 (22). ss. 40779-40808. Bibcode:2022OExpr..3040779P. doi:10.1364/OE.457139
![image]() . (PMID) 36299007.
. (PMID) 36299007. - ^ Popmintchev, Dimitar; Wang, Siyang; Xiaoshi, Zhang; Stoev, Ventzislav; Popmintchev, Tenio (30 Ağustos 2020). "Theory of the Chromatic Dispersion, Revisited" (İngilizce). arXiv:2011.00066 $2.
- Bibliyografi
- Cheng., David K. (2015). Köksal, Adnan; Saka, Birsen (Ed.). Fundamentals of Engineering Electromagnetics [Mühendislik Elektromanyetiğinin Temelleri] (2 bas.). Palme. ISBN .
- Pedrotti, Frank L.; Pedrotti, Leno M.; Pedrotti, Leno S. (2006). Introduction to Optics (İngilizce) (3 bas.). Pearson. ISBN .
- Pozar, David M. (2014). Köksal, Adnan; Saka (Ed.). Microwave Engineering [Mikrodalga Mühendisliği]. Palme. ISBN .
 | Optik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Elektromanyetizmada ve optikte dagilma ya da dispersiyon elektromanyetik dalganin ilerledigi ortamdaki faz hizinin frekansina bagli olmasi durumudur Kirilma indisinin frekansa bagliligi olarak da tanimlanabilmektedir Bu ozellige sahip ortamlar dagitici ortamlar olarak bilinir Faz hizi ile grup hizinin esit olmasi durumunda dagilma sifirlanir grup hizinin daha buyuk olmasi anormal dagilma olarak bilinir Iletim hatlari ve optik fiberler gibi dalga kilavuzlarinda dalga yayilimini buyuk olcude etkileyen dagilma dalga denkleminin gecerligi oldugu diger sistemlerde de gozlemlenebilmektedir Bir isik huzmesinin bir prizmada kirinimi Bu kirinimin nedeni malzeme dagilmasidir farkli frekanslardaki isik huzmeleri farkli acilarda kirilir Bir sistemdeki sinyal iletimi dagilma diyagrami ile gosterilebilir bu diyagram frekans ile dalga vektorunu iliskilendirir Farkli frekanslarin farkli faz hizlarinin olmasi ortam veya sistemde ilerleyen sinyallerde bozunmaya yol acar dusuk ve yuksek frekansli bilesenler farkli hizda hareket ettigi icin sinyal zarfi ilerleme ile birlikte genisler Dalga kilavuzlarindaki dagilma dalganin ilerledigi etken kirilma indisinin hesaplanmasi ile anlasilabilir Kayipsiz iletim hatlarinda dagilmasiz iletim kosullari telgrafcilar denklemleri ile hesaplanabilmektedir GaleriBir isik darbesinin dagilmali bir ortamda bozunmasi Dagilma ile gok kusagi olusumu Bir kirinim izgarasindan gecen ampul isiginin dagilmasiYuksek dagilim mertebelerinin genellestirilmis formulasyonu Kromatik dagilimin Taylor katsayilari araciligiyla perturbatif bir sekilde tanimlanmasi birkac farkli sistemden gelen dagilimin dengelenmesi gereken optimizasyon problemleri icin avantajlidir Ornegin chirp pulse lazer amplifikatorlerinde optik hasari onlemek icin pulslar once bir gerici tarafindan zaman icinde gerilir Daha sonra amplifikasyon surecinde darbeler kacinilmaz olarak malzemelerden gecen dogrusal ve dogrusal olmayan faz biriktirir Ve son olarak darbeler cesitli tipte kompresorlerde sikistirilir Biriken fazda kalan yuksek mertebeleri iptal etmek icin genellikle tek tek mertebeler olculur ve dengelenir Bununla birlikte duzgun sistemler icin bu tur perturbatif tanimlamaya genellikle ihtiyac duyulmaz ornegin dalga kilavuzlarinda yayilma Dagilim duzenleri Lah Laguerre tipi donusumler seklinde hesaplama dostu bir sekilde genellestirilmistir Dagilim mertebeleri fazin veya dalga vektorunun Taylor acilimi ile tanimlanir f w f w0 f w w0 w w0 12 2f w2 w0 w w0 2 1p pf wp w0 w w0 p displaystyle begin array c varphi mathrm omega mathrm varphi left right omega 0 left frac partial varphi partial omega right omega 0 left omega omega 0 right frac 1 2 left frac partial 2 varphi partial omega 2 right omega 0 left omega omega 0 right 2 ldots frac 1 p left frac partial p varphi partial omega p right omega 0 left omega omega 0 right p ldots end array k w k w0 k w w0 w w0 12 2k w2 w0 w w0 2 1p pk wp w0 w w0 p displaystyle begin array c k mathrm omega mathrm k left right omega 0 left frac partial k partial omega right omega 0 left omega omega 0 right frac 1 2 left frac partial 2 k partial omega 2 right omega 0 left omega omega 0 right 2 ldots frac 1 p left frac partial p k partial omega p right omega 0 left omega omega 0 right p ldots end array Dalga vektoru k w wcn w displaystyle k mathrm omega mathrm frac omega c n mathrm omega mathrm ve faz icin dagilim iliskileri f w wcOP w displaystyle varphi mathrm omega mathrm frac omega c it OP mathrm omega mathrm olarak ifade edilebilir p wpk w 1c p p 1 wp 1n w w p wpn w displaystyle begin array c frac partial p partial omega p k mathrm omega mathrm frac 1 c left p frac partial p 1 partial omega p 1 n mathrm omega mathrm omega frac partial p partial omega p n mathrm omega mathrm right end array p wpf w 1c p p 1 wp 1OP w w p wpOP w 1 displaystyle begin array c frac partial p partial omega p varphi mathrm omega mathrm frac 1 c left p frac partial p 1 partial omega p 1 it OP mathrm omega mathrm omega frac partial p partial omega p it OP mathrm omega mathrm right end array 1 Herhangi bir turevlenebilir fonksiyonun f w l displaystyle f mathrm omega mathrm lambda mathrm dalga boyu veya frekans uzayindaki turevleri bir Lah donusumu ile su sekilde belirtilir p wpf w 1 p l2pc p m 0pA p m lm m lmf l displaystyle begin array l frac partial p partial omega p f mathrm omega mathrm left mathrm mathrm 1 right p left frac lambda mathrm 2 pi c right p sum limits m 0 p mathcal A mathrm p m mathrm lambda m frac partial m partial lambda m f mathrm lambda mathrm end array displaystyle p lpf l 1 p w2pc p m 0pA p m wm m wmf w 2 displaystyle begin array c frac partial p partial lambda p f mathrm lambda mathrm left mathrm mathrm 1 right p left frac omega mathrm 2 pi c right p sum limits m 0 p mathcal A mathrm p m mathrm omega m frac partial m partial omega m f mathrm omega mathrm end array 2 Donusumun matris elemanlari Lah katsayilaridir A p m p p m m p 1 m 1 displaystyle mathcal A mathrm p m mathrm frac p mathrm left p mathrm m right mathrm m mathrm frac mathrm p mathrm mathrm 1 mathrm m mathrm mathrm 1 GDD icin yazilan yukaridaki ifade dalga boyu GGD olan bir sabitin sifir yuksek mertebeye sahip olacagini belirtir GDD den degerlendirilen yuksek mertebeler sunlardir p wpGDD w 1 p l2pc p m 0pA p m lm m lmGDD l displaystyle begin array c frac partial p partial omega p GDD mathrm omega mathrm left mathrm mathrm 1 right p left frac lambda mathrm 2 pi c right p sum limits m 0 p mathcal A mathrm p m mathrm lambda m frac partial m partial lambda m GDD mathrm lambda mathrm end array Kirilma indisi n displaystyle n veya optik yol OP displaystyle OP icin ifade edilen denklem 2 nin denklem 1 de yerine konmasi dagilim mertebeleri icin kapali form ifadeleri ile sonuclanir Genel olarak pth displaystyle p th mertebeli dagilim POD negatif iki mertebeli Laguerre tipi bir donusumdur POD dmf w dwm 1 p l2pc p 1 m 0pB p m l mdmOP l dlm displaystyle POD frac d m varphi omega d omega m 1 p frac lambda 2 pi c p 1 sum m 0 p mathcal B p m lambda m frac d m OP lambda d lambda m displaystyle POD dmk w dwm 1 p l2pc p 1 m 0pB p m l mdmn l dlm displaystyle POD frac d m k omega d omega m 1 p frac lambda 2 pi c p 1 sum m 0 p mathcal B p m lambda m frac d m n lambda d lambda m Donusumlerin matris elemanlari eksi 2 mertebesindeki isaretsiz Laguerre katsayilaridir ve su sekilde verilir B p m p p m m p 2 m 2 displaystyle mathcal B mathrm p m mathrm frac p mathrm left p mathrm m right mathrm m mathrm frac mathrm p mathrm mathrm 2 mathrm m mathrm mathrm 2 Dalga vektoru icin acikca yazilan ilk on dagilim mertebesi sunlardir GD wk w 1c n w w n w w 1c n l l n l l vgr 1 displaystyle begin array l boldsymbol it GD frac partial partial omega k mathrm omega mathrm frac mathrm 1 c left n mathrm omega mathrm omega frac partial n mathrm omega mathrm partial omega right frac mathrm 1 c left n mathrm lambda mathrm lambda frac partial n mathrm lambda mathrm partial lambda right v gr mathrm mathrm 1 end array Grup kirilma indisi ng displaystyle n g olarak tanimlanir ng cvgr 1 displaystyle n g cv gr mathrm mathrm 1 GDD 2 w2k w 1c 2 n w w w 2n w w2 1c l2pc l2 2n l l2 displaystyle begin array l boldsymbol it GDD frac partial 2 partial omega mathrm 2 k mathrm omega mathrm frac mathrm 1 c left mathrm 2 frac partial n mathrm omega mathrm partial omega omega frac partial 2 n mathrm omega mathrm partial omega mathrm 2 right frac mathrm 1 c left frac lambda mathrm 2 pi c right left lambda mathrm 2 frac partial 2 n mathrm lambda mathrm partial lambda mathrm 2 right end array TOD 3 w3k w 1c 3 2n w w2 w 3n w w3 1c l2pc 2 3l2 2n l l2 l3 3n l l3 displaystyle begin array l boldsymbol it TOD frac partial 3 partial omega mathrm 3 k mathrm omega mathrm frac mathrm 1 c left mathrm 3 frac partial 2 n mathrm omega mathrm partial omega mathrm 2 omega frac partial 3 n mathrm omega mathrm partial omega mathrm 3 right frac mathrm 1 c left frac lambda mathrm 2 pi c right mathrm 2 Bigl mathrm 3 lambda mathrm 2 frac partial 2 n mathrm lambda mathrm partial lambda mathrm 2 lambda mathrm 3 frac partial 3 n mathrm lambda mathrm partial lambda mathrm 3 Bigr end array FOD 4 w4k w 1c 4 3n w w3 w 4n w w4 1c l2pc 3 12l2 2n l l2 8l3 3n l l3 l4 4n l l4 displaystyle begin array l boldsymbol it FOD frac partial 4 partial omega mathrm 4 k mathrm omega mathrm frac mathrm 1 c left mathrm 4 frac partial 3 n mathrm omega mathrm partial omega mathrm 3 omega frac partial 4 n mathrm omega mathrm partial omega mathrm 4 right frac mathrm 1 c left frac lambda mathrm 2 pi c right mathrm 3 Bigl mathrm 12 lambda mathrm 2 frac partial 2 n mathrm lambda mathrm partial lambda mathrm 2 mathrm 8 lambda mathrm 3 frac partial 3 n mathrm lambda mathrm partial lambda mathrm 3 lambda mathrm 4 frac partial 4 n mathrm lambda mathrm partial lambda mathrm 4 Bigr end array FiOD 5 w5k w 1c 5 4n w w4 w 5n w w5 1c l2pc 4 60l2 2n l l2 60l3 3n l l3 15l4 4n l l4 l5 5n l l5 displaystyle begin array l boldsymbol it FiOD frac partial 5 partial omega mathrm 5 k mathrm omega mathrm frac mathrm 1 c left mathrm 5 frac partial 4 n mathrm omega mathrm partial omega mathrm 4 omega frac partial 5 n mathrm omega mathrm partial omega mathrm 5 right frac mathrm 1 c left frac lambda mathrm 2 pi c right mathrm 4 Bigl mathrm 60 lambda mathrm 2 frac partial 2 n mathrm lambda mathrm partial lambda mathrm 2 mathrm 60 lambda mathrm 3 frac partial 3 n mathrm lambda mathrm partial lambda mathrm 3 mathrm 15 lambda mathrm 4 frac partial 4 n mathrm lambda mathrm partial lambda mathrm 4 lambda mathrm 5 frac partial 5 n mathrm lambda mathrm partial lambda mathrm 5 Bigr end array SiOD 6 w6k w 1c 6 5n w w5 w 6n w w6 1c l2pc 5 360l2 2n l l2 480l3 3n l l3 180l4 4n l l4 24l5 5n l l5 l6 6n l l6 displaystyle begin array l boldsymbol it SiOD frac partial 6 partial omega mathrm 6 k mathrm omega mathrm frac mathrm 1 c left mathrm 6 frac partial 5 n mathrm omega mathrm partial omega mathrm 5 omega frac partial 6 n mathrm omega mathrm partial omega mathrm 6 right frac mathrm 1 c left frac lambda mathrm 2 pi c right mathrm 5 Bigl mathrm 360 lambda mathrm 2 frac partial 2 n mathrm lambda mathrm partial lambda mathrm 2 mathrm 480 lambda mathrm 3 frac partial 3 n mathrm lambda mathrm partial lambda mathrm 3 mathrm 180 lambda mathrm 4 frac partial 4 n mathrm lambda mathrm partial lambda mathrm 4 mathrm 24 lambda mathrm 5 frac partial 5 n mathrm lambda mathrm partial lambda mathrm 5 lambda mathrm 6 frac partial 6 n mathrm lambda mathrm partial lambda mathrm 6 Bigr end array SeOD 7 w7k w 1c 7 6n w w6 w 7n w w7 1c l2pc 6 2520l2 2n l l2 4200l3 3n l l3 2100l4 4n l l4 420l5 5n l l5 35l6 6n l l6 l7 7n l l7 displaystyle begin array l boldsymbol it SeOD frac partial 7 partial omega mathrm 7 k mathrm omega mathrm frac mathrm 1 c left mathrm 7 frac partial 6 n mathrm omega mathrm partial omega mathrm 6 omega frac partial 7 n mathrm omega mathrm partial omega mathrm 7 right frac mathrm 1 c left frac lambda mathrm 2 pi c right mathrm 6 Bigl mathrm 2520 lambda mathrm 2 frac partial 2 n mathrm lambda mathrm partial lambda mathrm 2 mathrm 4200 lambda mathrm 3 frac partial 3 n mathrm lambda mathrm partial lambda mathrm 3 mathrm 2100 lambda mathrm 4 frac partial 4 n mathrm lambda mathrm partial lambda mathrm 4 mathrm 420 lambda mathrm 5 frac partial 5 n mathrm lambda mathrm partial lambda mathrm 5 mathrm 35 lambda mathrm 6 frac partial 6 n mathrm lambda mathrm partial lambda mathrm 6 lambda mathrm 7 frac partial 7 n mathrm lambda mathrm partial lambda mathrm 7 Bigr end array EOD 8 w8k w 1c 8 7n w w7 w 8n w w8 1c l2pc 7 20160l2 2n l l2 40320l3 3n l l3 25200l4 4n l l4 6720l5 5n l l5 840l6 6n l l6 48l7 7n l l7 l8 8n l l8 displaystyle begin array l boldsymbol it EOD frac partial 8 partial omega mathrm 8 k mathrm omega mathrm frac mathrm 1 c left mathrm 8 frac partial 7 n mathrm omega mathrm partial omega mathrm 7 omega frac partial 8 n mathrm omega mathrm partial omega mathrm 8 right frac mathrm 1 c left frac lambda mathrm 2 pi c right mathrm 7 Bigl mathrm 20160 lambda mathrm 2 frac partial 2 n mathrm lambda mathrm partial lambda mathrm 2 mathrm 40320 lambda mathrm 3 frac partial 3 n mathrm lambda mathrm partial lambda mathrm 3 mathrm 25200 lambda mathrm 4 frac partial 4 n mathrm lambda mathrm partial lambda mathrm 4 mathrm 6720 lambda mathrm 5 frac partial 5 n mathrm lambda mathrm partial lambda mathrm 5 mathrm 840 lambda mathrm 6 frac partial 6 n mathrm lambda mathrm partial lambda mathrm 6 mathrm 48 lambda mathrm 7 frac partial 7 n mathrm lambda mathrm partial lambda mathrm 7 lambda mathrm 8 frac partial 8 n mathrm lambda mathrm partial lambda mathrm 8 Bigr end array NOD 9 w9k w 1c 9 8n w w8 w 9n w w9 1c l2pc 8 181440l2 2n l l2 423360l3 3n l l3 317520l4 4n l l4 105840l5 5n l l5 17640l6 6n l l6 1512l7 7n l l7 63l8 8n l l8 l9 9n l l9 displaystyle begin array l boldsymbol it NOD frac partial 9 partial omega mathrm 9 k mathrm omega mathrm frac mathrm 1 c left mathrm 9 frac partial 8 n mathrm omega mathrm partial omega mathrm 8 omega frac partial 9 n mathrm omega mathrm partial omega mathrm 9 right frac mathrm 1 c left frac lambda mathrm 2 pi c right mathrm 8 Bigl mathrm 181440 lambda mathrm 2 frac partial 2 n mathrm lambda mathrm partial lambda mathrm 2 mathrm 423360 lambda mathrm 3 frac partial 3 n mathrm lambda mathrm partial lambda mathrm 3 mathrm 317520 lambda mathrm 4 frac partial 4 n mathrm lambda mathrm partial lambda mathrm 4 mathrm 105840 lambda mathrm 5 frac partial 5 n mathrm lambda mathrm partial lambda mathrm 5 mathrm 17640 lambda mathrm 6 frac partial 6 n mathrm lambda mathrm partial lambda mathrm 6 mathrm 1512 lambda mathrm 7 frac partial 7 n mathrm lambda mathrm partial lambda mathrm 7 mathrm 63 lambda mathrm 8 frac partial 8 n mathrm lambda mathrm partial lambda mathrm 8 lambda mathrm 9 frac partial 9 n mathrm lambda mathrm partial lambda mathrm 9 Bigr end array TeOD 10 w10k w 1c 10 9n w w9 w 10n w w10 1c l2pc 9 1814400l2 2n l l2 4838400l3 3n l l3 4233600l4 4n l l4 1693440l5 5n l l5 352800l6 6n l l6 40320l7 7n l l7 2520l8 8n l l8 80l9 9n l l9 l10 10n l l10 displaystyle begin array l boldsymbol it TeOD frac partial 10 partial omega mathrm 10 k mathrm omega mathrm frac mathrm 1 c left mathrm 10 frac partial 9 n mathrm omega mathrm partial omega mathrm 9 omega frac partial 10 n mathrm omega mathrm partial omega mathrm 10 right frac mathrm 1 c left frac lambda mathrm 2 pi c right mathrm 9 Bigl mathrm 1814400 lambda mathrm 2 frac partial 2 n mathrm lambda mathrm partial lambda mathrm 2 mathrm 4838400 lambda mathrm 3 frac partial 3 n mathrm lambda mathrm partial lambda mathrm 3 mathrm 4233600 lambda mathrm 4 frac partial 4 n mathrm lambda mathrm partial lambda mathrm 4 1693440 lambda mathrm 5 frac partial 5 n mathrm lambda mathrm partial lambda mathrm 5 mathrm 352800 lambda mathrm 6 frac partial 6 n mathrm lambda mathrm partial lambda mathrm 6 mathrm 40320 lambda mathrm 7 frac partial 7 n mathrm lambda mathrm partial lambda mathrm 7 mathrm 2520 lambda mathrm 8 frac partial 8 n mathrm lambda mathrm partial lambda mathrm 8 mathrm 80 lambda mathrm 9 frac partial 9 n mathrm lambda mathrm partial lambda mathrm 9 lambda mathrm 10 frac partial 10 n mathrm lambda mathrm partial lambda mathrm 10 Bigr end array Acikca f displaystyle varphi fazi icin yazilan ilk on dagilim derecesi Lah donusumleri denklem 2 kullanilarak dalga boyunun bir fonksiyonu olarak su sekilde ifade edilebilir p wpf w 1 p l2pc p m 0pA p m lm m lmf l displaystyle begin array l frac partial p partial omega p f mathrm omega mathrm left mathrm mathrm 1 right p left frac lambda mathrm 2 pi c right p sum limits m 0 p mathcal A mathrm p m mathrm lambda m frac partial m partial lambda m f mathrm lambda mathrm end array displaystyle p lpf l 1 p w2pc p m 0pA p m wm m wmf w displaystyle begin array c frac partial p partial lambda p f mathrm lambda mathrm left mathrm mathrm 1 right p left frac omega mathrm 2 pi c right p sum limits m 0 p mathcal A mathrm p m mathrm omega m frac partial m partial omega m f mathrm omega mathrm end array f w w 2pcw2 f w l l22pc f l l displaystyle begin array l frac partial varphi mathrm omega mathrm partial omega left frac mathrm 2 pi c omega mathrm 2 right frac partial varphi mathrm omega mathrm partial lambda left frac lambda mathrm 2 mathrm 2 pi c right frac partial varphi mathrm lambda mathrm partial lambda end array 2f w w2 w f w w l2pc 2 2l f l l l2 2f l l2 displaystyle begin array l frac partial 2 varphi mathrm omega mathrm partial omega mathrm 2 frac partial partial omega left frac partial varphi mathrm omega mathrm partial omega right left frac lambda mathrm 2 pi c right mathrm 2 left mathrm 2 lambda frac partial varphi mathrm lambda mathrm partial lambda lambda mathrm 2 frac partial 2 varphi mathrm lambda mathrm partial lambda mathrm 2 right end array 3f w w3 l2pc 3 6l f l l 6l2 2f l l2 l3 3f l l3 displaystyle begin array l frac partial 3 varphi mathrm omega mathrm partial omega mathrm 3 left frac lambda mathrm 2 pi c right mathrm 3 left mathrm 6 lambda frac partial varphi mathrm lambda mathrm partial lambda mathrm 6 lambda mathrm 2 frac partial 2 varphi mathrm lambda mathrm partial lambda mathrm 2 lambda mathrm 3 frac partial 3 varphi mathrm lambda mathrm partial lambda mathrm 3 right end array 4f w w4 l2pc 4 24l f l l 36l2 2f l l2 12l3 3f l l3 l4 4f l l4 displaystyle begin array l frac partial 4 varphi mathrm omega mathrm partial omega mathrm 4 left frac lambda mathrm 2 pi c right mathrm 4 Bigl mathrm 24 lambda frac partial varphi mathrm lambda mathrm partial lambda mathrm 36 lambda mathrm 2 frac partial 2 varphi mathrm lambda mathrm partial lambda mathrm 2 mathrm 12 lambda mathrm 3 frac partial 3 varphi mathrm lambda mathrm partial lambda mathrm 3 lambda mathrm 4 frac partial 4 varphi mathrm lambda mathrm partial lambda mathrm 4 Bigr end array 5f w w5 l2pc 5 120l f l l 240l2 2f l l2 120l3 3f l l3 20l4 4f l l4 l5 5f l l5 displaystyle begin array l frac partial mathrm 5 varphi mathrm omega mathrm partial omega mathrm 5 left frac lambda mathrm 2 pi c right mathrm 5 Bigl mathrm 120 lambda frac partial varphi mathrm lambda mathrm partial lambda mathrm 240 lambda mathrm 2 frac partial 2 varphi mathrm lambda mathrm partial lambda mathrm 2 mathrm 120 lambda mathrm 3 frac partial 3 varphi mathrm lambda mathrm partial lambda mathrm 3 mathrm 20 lambda mathrm 4 frac partial 4 varphi mathrm lambda mathrm partial lambda mathrm 4 lambda mathrm 5 frac partial 5 varphi mathrm lambda mathrm partial lambda mathrm 5 Bigr end array 6f w w6 l2pc 6 720l f l l 1800l2 2f l l2 1200l3 3f l l3 300l4 4f l l4 30l5 5f l l5 l6 6f l l6 displaystyle begin array l frac partial 6 varphi mathrm omega mathrm partial omega mathrm 6 left frac lambda mathrm 2 pi c right mathrm 6 Bigl mathrm 720 lambda frac partial varphi mathrm lambda mathrm partial lambda mathrm 1800 lambda mathrm 2 frac partial 2 varphi mathrm lambda mathrm partial lambda mathrm 2 mathrm 1200 lambda mathrm 3 frac partial 3 varphi mathrm lambda mathrm partial lambda mathrm 3 mathrm 300 lambda mathrm 4 frac partial 4 varphi mathrm lambda mathrm partial lambda mathrm 4 mathrm 30 lambda mathrm 5 frac partial 5 varphi mathrm lambda mathrm partial lambda mathrm 5 mathrm lambda mathrm 6 frac partial 6 varphi mathrm lambda mathrm partial lambda mathrm 6 Bigr end array 7f w w7 l2pc 7 5040l f l l 15120l2 2f l l2 12600l3 3f l l3 4200l4 4f l l4 630l5 5f l l5 42l6 6f l l6 l7 7f l l7 displaystyle begin array l frac partial 7 varphi mathrm omega mathrm partial omega mathrm 7 left frac lambda mathrm 2 pi c right mathrm 7 Bigl mathrm 5040 lambda frac partial varphi mathrm lambda mathrm partial lambda mathrm 15120 lambda mathrm 2 frac partial 2 varphi mathrm lambda mathrm partial lambda mathrm 2 mathrm 12600 lambda mathrm 3 frac partial 3 varphi mathrm lambda mathrm partial lambda mathrm 3 mathrm 4200 lambda mathrm 4 frac partial 4 varphi mathrm lambda mathrm partial lambda mathrm 4 mathrm 630 lambda mathrm 5 frac partial 5 varphi mathrm lambda mathrm partial lambda mathrm 5 mathrm 42 lambda mathrm 6 frac partial 6 varphi mathrm lambda mathrm partial lambda mathrm 6 lambda mathrm 7 frac partial 7 varphi mathrm lambda mathrm partial lambda mathrm 7 Bigr end array 8f w w8 l2pc 8 40320l f l l 141120l2 2f l l2 141120l3 3f l l3 58800l4 4f l l4 11760l5 5f l l5 1176l6 6f l l6 56l7 7f l l7 l8 8f l l8 displaystyle begin array l frac partial 8 varphi mathrm omega mathrm partial omega mathrm 8 left frac lambda mathrm 2 pi c right mathrm 8 Bigl mathrm 40320 lambda frac partial varphi mathrm lambda mathrm partial lambda mathrm 141120 lambda mathrm 2 frac partial 2 varphi mathrm lambda mathrm partial lambda mathrm 2 mathrm 141120 lambda mathrm 3 frac partial 3 varphi mathrm lambda mathrm partial lambda mathrm 3 mathrm 58800 lambda mathrm 4 frac partial 4 varphi mathrm lambda mathrm partial lambda mathrm 4 mathrm 11760 lambda mathrm 5 frac partial 5 varphi mathrm lambda mathrm partial lambda mathrm 5 mathrm 1176 lambda mathrm 6 frac partial 6 varphi mathrm lambda mathrm partial lambda mathrm 6 mathrm 56 lambda mathrm 7 frac partial 7 varphi mathrm lambda mathrm partial lambda mathrm 7 lambda mathrm 8 frac partial 8 varphi mathrm lambda mathrm partial lambda mathrm 8 Bigr end array 9f w w9 l2pc 9 362880l f l l 1451520l2 2f l l2 1693440l3 3f l l3 846720l4 4f l l4 211680l5 5f l l5 28224l6 6f l l6 2016l7 7f l l7 72l8 8f l l8 l9 9f l l9 displaystyle begin array l frac partial 9 varphi mathrm omega mathrm partial omega mathrm 9 left frac lambda mathrm 2 pi c right mathrm 9 Bigl mathrm 362880 lambda frac partial varphi mathrm lambda mathrm partial lambda mathrm 1451520 lambda mathrm 2 frac partial 2 varphi mathrm lambda mathrm partial lambda mathrm 2 mathrm 1693440 lambda mathrm 3 frac partial 3 varphi mathrm lambda mathrm partial lambda mathrm 3 mathrm 846720 lambda mathrm 4 frac partial 4 varphi mathrm lambda mathrm partial lambda mathrm 4 mathrm 211680 lambda mathrm 5 frac partial 5 varphi mathrm lambda mathrm partial lambda mathrm 5 mathrm 28224 lambda mathrm 6 frac partial 6 varphi mathrm lambda mathrm partial lambda mathrm 6 mathrm 2016 lambda mathrm 7 frac partial 7 varphi mathrm lambda mathrm partial lambda mathrm 7 mathrm 72 lambda mathrm 8 frac partial 8 varphi mathrm lambda mathrm partial lambda mathrm 8 lambda mathrm 9 frac partial mathrm 9 varphi mathrm lambda mathrm partial lambda mathrm 9 Bigr end array 10f w w10 l2pc 10 3628800l f l l 16329600l2 2f l l2 21772800l3 3f l l3 12700800l4 4f l l4 3810240l5 5f l l5 635040l6 6f l l6 60480l7 7f l l7 3240l8 8f l l8 90l9 9f l l9 l10 10f l l10 displaystyle begin array l frac partial 10 varphi mathrm omega mathrm partial omega mathrm 10 left frac lambda mathrm 2 pi c right mathrm 10 Bigl mathrm 3628800 lambda frac partial varphi mathrm lambda mathrm partial lambda mathrm 16329600 lambda mathrm 2 frac partial 2 varphi mathrm lambda mathrm partial lambda mathrm 2 mathrm 21772800 lambda mathrm 3 frac partial 3 varphi mathrm lambda mathrm partial lambda mathrm 3 mathrm 12700800 lambda mathrm 4 frac partial 4 varphi mathrm lambda mathrm partial lambda mathrm 4 mathrm 3810240 lambda mathrm 5 frac partial 5 varphi mathrm lambda mathrm partial lambda mathrm 5 mathrm 635040 lambda mathrm 6 frac partial 6 varphi mathrm lambda mathrm partial lambda mathrm 6 mathrm 60480 lambda mathrm 7 frac partial 7 varphi mathrm lambda mathrm partial lambda mathrm 7 mathrm 3240 lambda mathrm 8 frac partial 8 varphi mathrm lambda mathrm partial lambda mathrm 8 mathrm 90 lambda mathrm 9 frac partial 9 varphi mathrm lambda mathrm partial lambda mathrm 9 lambda mathrm 10 frac partial 10 varphi mathrm lambda mathrm partial lambda mathrm 10 Bigr end array Ayrica bakinizWikimedia Commons ta Dagilma ile ilgili ortam dosyalari bulunmaktadir Faz hizi Grup hizi Kirinim Kramers Kronig iliskileriKaynakca Cheng 2015 s 297 Pozar 2014 s 150 Cheng 2015 s 396 Pedrotti Pedrotti amp Pedrotti 2006 ss 253 260 Pozar 2014 s 49 56 Popmintchev Dimitar Wang Siyang Xiaoshi Zhang Stoev Ventzislav Popmintchev Tenio 24 Ekim 2022 Analytical Lah Laguerre optical formalism for perturbative chromatic dispersion Ingilizce 30 22 ss 40779 40808 Bibcode 2022OExpr 3040779P doi 10 1364 OE 457139 PMID 36299007 Popmintchev Dimitar Wang Siyang Xiaoshi Zhang Stoev Ventzislav Popmintchev Tenio 30 Agustos 2020 Theory of the Chromatic Dispersion Revisited Ingilizce arXiv 2011 00066 2 BibliyografiCheng David K 2015 Koksal Adnan Saka Birsen Ed Fundamentals of Engineering Electromagnetics Muhendislik Elektromanyetiginin Temelleri 2 bas Palme ISBN 978 975 8982 99 8 Pedrotti Frank L Pedrotti Leno M Pedrotti Leno S 2006 Introduction to Optics Ingilizce 3 bas Pearson ISBN 9780131499331 Pozar David M 2014 Koksal Adnan Saka Ed Microwave Engineering Mikrodalga Muhendisligi Palme ISBN 9786053552499 Optik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State



