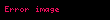Parçacık fiziğinde, Fermi etkileşimi (aynı zamanda beta bozunmasının Fermi teorisi veya Fermi ) beta bozunmasının 1933'te Enrico Fermi tarafından önerilmiş bir açıklamasıdır. Teori, dört fermiyonun (ilişkili Feynman diyagramının bir köşesinde) birbiriyle direkt etkileştiğini varsayar. Bu etkileşim bir nötronun bir elektron, bir nötrino (daha sonra bir antinötrino olduğu belirlendi) ve bir protonla doğrudan bağlanmasıyla bir nötronun beta bozunmasını açıklar.

β-
bozunması (Eşlik eden antinötrino çıkarılmıştır). Görsel, bir serbest nötronun beta bozunmasını gösterir. İki olayda da, sanal
W-
bozonunun (daha sonra elektron ve antinötrinoya bozunan) orta düzey yayılımı gösterilmemiştir.
Fermi bu bağlanmadan ilk olarak 1933'te beta bozunmasının tanımını yaparken bahsetti. Fermi etkileşimi, proton-nötron ve elektron-antiötrino arasındaki etkileşimin, Fermi teorisinin düşük enerjili etkili alan teorisi olduğu sanal bir W⁻ bozonunun aracılık ettiği zayıf etkileşim teorisinin habercisiydi.
İlk ret ve sonraki yayın tarihi
Fermi ilk olarak "okuyucunun ilgisini çekemeyecek kadar gerçeklikten uzak spekülasyonlar içerdiği" için reddedilen beta bozunmasının "geçici" teorisini prestijli bir bilim dergisi olan Nature'de yayınladı.Nature daha sonra bu reddi kendi tarihindeki en büyük editör hatalarından biri olduğunu kabul etti. Daha sonra Fermi, revize edilmiş versiyonları İtalyan ve Alman yayıncılara sundu ve yayınlar bunları kabul edip 1933 ve 1934'te bu dillerde yayınladı. Makale, o sırada İngilizce birincil yayında yer almadı. Bu ufuk açıcı makalenin İngilizce çevirisi American Journal of Physics'te 1968 tarihinde yayınlandı.
Fermi fark etti ki makalenin asıl reddini o kadar rahatsız edici buldu ki, teorik fizikten biraz ara vermeye ve sadece deneysel fizik yapmaya karar verdi. Bu, kısa bir süre sonra, yavaş nötronlarla ile ilgili ünlü çalışmasına yol açacaktır.
"Geçici"
Tanımlar
Teori, doğrudan etkileşim içinde olduğu varsayılan üç tür parçacıkla ilgilenir: başlangıçta (

Elektron durumu
'nin olduğu ve
olduğu yerde:

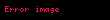


Nötrino durumu
Benzer olarak,

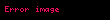




Ağır parçacık durumu

bir nötronu temsil eder ve
bir protonu temsil eder (temsil edilişte 
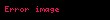
Ağır bir parçacığı bir protondan nötrona ve tersi yönde değiştiren operatörler sırasıyla şu şekilde temsil edilir:
ve



Hamiltonyen
Hamiltonyen, üç parçadan oluşur: özgür ağır parçacıkların enerjisini temsil eden 
enerjisini temsil eden 






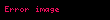
Nükleusun Coulomb alanında 



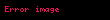


Etkileşim kısmı, bir elektronun ve bir nötrinonun (şimdi bir antinötrino olarak bilinir) emisyonu ile birlikte bir protonun bir nötrona dönüşümünü temsil eden bir terim ve ayrıca ters işlem için bir terim içermelidir; elektron ve proton arasındaki Coulomb kuvveti, 
Fermi, 
ve daha sonra, hafif parçacıkların dört bileşenli olduğunu, ancak ağır parçacıkların hızı 




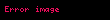
Matris elementleri
Sistemin durumu, 






rölativist versiyonunu kullanarak 




burada integral, ağır parçacıkların tüm konfigürasyon uzayını kaplar (hariç 

Değişim olasılığı
Bilinen göre 


göre[],bu değişimin olasılığı

Bütün pozitif enerjili nötrino spin / momentum yönlerinin (burada 


Bu değişmenin olasılığının 




Fermi, bu fonksiyon hakkında üç açıklama yapmıştır:
- Nötrino durumları serbest kabul edildiğinden,
ve böylece sürekli
-spektrumundaki üst limit ise
değeridir.
elektronları için
-bozunumunun oluşması için proton-nötron enerji farkının
olması gerekir.
- Geçiş olasılığındaki
- faktörü normalde 1 büyüklüğündedir, ancak özel durumlarda yok olur; bu,
-bozunumu için (yaklaşık) seçim kurallarına yol açar.
Yasaklı değişimler
Yukarıda da not edildiği gibi, ne zaman 


Çekirdeğin, protonların ve nötronların bireysel kuantum durumları açısından tanımlanması iyiyse, 


Etkisi
Kısa bir süre sonra Fermi'nin makalesi yayımlandı, Werner Heisenberg'ün Wolfgang Pauli'ye yazdığı bir mektupta, çekirdekteki nötrinoların ve elektronların yayımlanması ve soğurulmasının, karışıklık teorisinin ikinci mertebesinde, protonlar ve nötronlar arasında, emisyonun nasıl olduğuna benzer şekilde, bir çekime yol açması gerektiğini ve fotonların absorpsiyonu elektromanyetik kuvvete yol açtığını kaydetti. Kuvvetin 
Aynı yılda, Hideki Yukawa bu fikre kapıldı, ancak nötrinolar ve elektronlar, durağan kütlesi elektrondan yaklaşık 200 kat daha ağır olan varsayımsal yeni bir parçacık ile değiştirildi.
Sonraki gelişmeler
Fermi'nin dörtlü-fermiyon teorisi, zayıf etkileşimi oldukça iyi bir şekilde açıklar. Maalesef, hesaplanan kesit veya etkileşimin olasılığı, 

Etkileşim ayrıca müon bozunmasını, etkileşimin aynı temel gücüne sahip bir müon, elektron-antinötrino, müon-nötrino ve elektronun birleşmesi yoluyla da açıklayabilir. Bu hipotez Gershtein ve Zeldovich tarafından öne sürüldü ve Vektör akımının korunması hipotezi olarak da bilinir.
Orijinal teoride Fermi, etkileşimin biçiminin iki vektör akımının temas kuplajı olduğunu varsaydı. Daha sonrasında, Lee ve Yang tarafından eksenel, pariteyi ihlal eden bir akımın ortaya çıkmasını hiçbir şeyin engellemediğine dikkat çekildi ve bu, Chien-Shiung Wu tarafından yürütülen deneylerle doğrulandı.
Fermi sabiti
Fermi sabitinin en kesin deneysel tespiti, GF değerinin karesiyle ters orantılı olan (müon kütlesini W bozonunun kütlesine karşı ihmal ederken) müon ömrünün ölçümleri ile elde edilir. Modern terimlerle, "indirgenmiş Fermi sabiti", yani doğal birimlerdeki sabit
değeridir. Burada, g, zayıf etkileşimin çiftlenim sabitidir ve MW ise söz konusu bozunmaya aracılık eden W bozonunun kütlesidir.
Standart Modelde, Fermi sabiti Higgs vakum beklenti değeridir
.
Daha doğrudan, yaklaşık olarak (standart model için ağaç düzeyi),
Bu, W ve Z bozonları ile 
Kaynakça
- ^ Yang (2012). "Fermi's β-decay Theory". Asia Pacific Physics Newsletter. 1 (1): 27-30. doi:10.1142/s2251158x12000045.
- ^ Theory of Fundamental Processes. . 1962. Yazar
|ad1=eksik|soyadı1=() - ^ a b Introduction to Elementary Particles. 2nd. 2009. ss. 314-315. ISBN . Yazar
|ad1=eksik|soyadı1=() - ^ Inward Bound. Oxford: Oxford University Press. 1986. s. 418. ISBN .
- ^ a b Neutrino. Oxford University Press. 23 Şubat 2012. Erişim tarihi: 5 Mayıs 2017. Yazar
|ad1=eksik|soyadı1=()[] - ^ "Tentativo di una teoria dei raggi β". (İtalyanca). 2 (12). 1933. Birden fazla yazar-name-list parameters kullanıldı (); Yazar
|ad1=eksik|soyadı1=() - ^ "Tentativo di una teoria dei raggi β". (İtalyanca). 11 (1): 1-19. 1934. doi:10.1007/BF02959820. Birden fazla yazar-name-list parameters kullanıldı (); Yazar
|ad1=eksik|soyadı1=() - ^ "Versuch einer Theorie der beta-Strahlen. I". Zeitschrift für Physik (Almanca). 88 (3–4): 161. 1934. doi:10.1007/BF01351864. Birden fazla yazar-name-list parameters kullanıldı (); Yazar
|ad1=eksik|soyadı1=() - ^ a b "Fermi's Theory of Beta Decay". American Journal of Physics. 36 (12): 1150-1160. 1968. doi:10.1119/1.1974382. 12 Mayıs 2013 tarihinde kaynağından . Erişim tarihi: 29 Ocak 2023. Birden fazla yazar-name-list parameters kullanıldı (); Yazar
|ad1=eksik|soyadı1=() Includes complete English translation of Fermi's 1934 paper in German - ^ Scientific Correspondence with Bohr, Einstein, Heisenberg a.o. Volume II:1930–1939. Springer-Verlag Berlin Heidelberg GmbH. 1985. Yazar
|ad1=eksik|soyadı1=() - ^ The Origin of the Concept of Nuclear Forces. Institute of Physics Publishing. 1996. Yazar
|ad1=eksik|soyadı1=() - ^ "On the interaction of elementary particles. I.". Proceedings of the Physico-Mathematical Society of Japan (İngilizce). 17: 1. 1935. Birden fazla yazar-name-list parameters kullanıldı (); Yazar
|ad1=eksik|soyadı1=() - ^ The Historical Development of Quantum Theory, Volume 6 Part 2 (1932–1941). Springer. 2001. Yazar
|ad1=eksik|soyadı1=() - ^ Gerstein (1955). "Meson corrections in the theory of beta decay". : 698-699.
- ^ Lee (1956). "Question of Parity Conservation in Weak Interactions". Physical Review. 104 (1): 254-258. doi:10.1103/PhysRev.104.254.
- ^ Wu (1957). "Experimental Test of Parity Conservation in Beta Decay". Physical Review. 105 (4): 1413-1415. doi:10.1103/PhysRev.105.1413.
- ^ MuLan Collaboration (2007). "Improved Measurement of the Positive-Muon Lifetime and Determination of the Fermi Constant". Physical Review Letters. 99 (3): 032001. arXiv:0704.1981 $2. doi:10.1103/PhysRevLett.99.032001. (PMID) 17678280. Birden fazla yazar-name-list parameters kullanıldı (); Yazar
|ad1=eksik|soyadı1=(); Yazar eksik|soyadı2=() - ^ . The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. June 2015. 11 Aralık 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 31 Ekim 2016.
- ^ Plehn (2005). "Quartic Higgs coupling at hadron colliders". Physical Review D. 72 (5): 053008. arXiv:hep-ph/0507321 $2. doi:10.1103/PhysRevD.72.053008.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Parcacik fiziginde Fermi etkilesimi ayni zamanda beta bozunmasinin Fermi teorisi veya Fermi beta bozunmasinin 1933 te Enrico Fermi tarafindan onerilmis bir aciklamasidir Teori dort fermiyonun iliskili Feynman diyagraminin bir kosesinde birbiriyle direkt etkilestigini varsayar Bu etkilesim bir notronun bir elektron bir notrino daha sonra bir antinotrino oldugu belirlendi ve bir protonla dogrudan baglanmasiyla bir notronun beta bozunmasini aciklar Bir atom cekirdeginde b bozunmasi Eslik eden antinotrino cikarilmistir Gorsel bir serbest notronun beta bozunmasini gosterir Iki olayda da sanal W bozonunun daha sonra elektron ve antinotrinoya bozunan orta duzey yayilimi gosterilmemistir Fermi bu baglanmadan ilk olarak 1933 te beta bozunmasinin tanimini yaparken bahsetti Fermi etkilesimi proton notron ve elektron antiotrino arasindaki etkilesimin Fermi teorisinin dusuk enerjili etkili alan teorisi oldugu sanal bir W bozonunun aracilik ettigi zayif etkilesim teorisinin habercisiydi Ilk ret ve sonraki yayin tarihiFermi ilk olarak okuyucunun ilgisini cekemeyecek kadar gerceklikten uzak spekulasyonlar icerdigi icin reddedilen beta bozunmasinin gecici teorisini prestijli bir bilim dergisi olan Nature de yayinladi Nature daha sonra bu reddi kendi tarihindeki en buyuk editor hatalarindan biri oldugunu kabul etti Daha sonra Fermi revize edilmis versiyonlari Italyan ve Alman yayincilara sundu ve yayinlar bunlari kabul edip 1933 ve 1934 te bu dillerde yayinladi Makale o sirada Ingilizce birincil yayinda yer almadi Bu ufuk acici makalenin Ingilizce cevirisi American Journal of Physics te 1968 tarihinde yayinlandi Fermi fark etti ki makalenin asil reddini o kadar rahatsiz edici buldu ki teorik fizikten biraz ara vermeye ve sadece deneysel fizik yapmaya karar verdi Bu kisa bir sure sonra yavas notronlarla ile ilgili unlu calismasina yol acacaktir Gecici Tanimlar Teori dogrudan etkilesim icinde oldugu varsayilan uc tur parcacikla ilgilenir baslangicta r 1 displaystyle rho 1 notron durumu ndaki bir agir parcacik daha sonra bir elektron ve bir notrino emisyonu ile proton durumu r 1 displaystyle rho 1 e gecis yapar Elektron durumu ps displaystyle psi nin oldugu ve pss displaystyle psi s oldugu yerde ps spssas displaystyle psi sum s psi s a s as displaystyle a s su sekilde etki eden lt span about mwt86 class mwe math element data mw amp quot name amp quot amp quot math amp quot amp quot attrs amp quot amp quot body amp quot amp quot extsrc amp quot amp quot s amp quot id mwWg typeof mw Extension math gt lt span class mwe math mathml inline mwe math mathml a11y style display none gt lt math alttext displaystyle s xmlns http www w3 org 1998 Math MathML gt lt semantics gt lt mrow class MJX TeXAtom ORD gt lt mstyle displaystyle true scriptlevel 0 gt lt mi gt s lt mi gt lt mstyle gt lt mrow gt lt annotation encoding application x tex gt displaystyle s lt annotation gt lt semantics gt lt math gt lt span gt lt img alt s aria hidden true class mwe math fallback image inline data cx amp quot adapted amp quot false src https www wikipedia tr tr nina az image aHR0cHM6Ly93aWtpbWVkaWEub3JnL2FwaS9yZXN0X3YxL21lZGlhL21hdGgvcmVuZGVyL3N2Zy8wMWQxMzFkZmQ3NjczOTM4Yjk0NzA3MmExM2E5NzQ0ZmU5OTdlNjMy svg style vertical align 0 338ex width 1 09ex height 1 676ex gt lt span gt durumundaki bir elektronu yok eden operatordur asPS N1 N2 Ns 1 N1 N2 Ns 1 1 Ns PS N1 N2 1 Ns displaystyle a s Psi N 1 N 2 ldots N s ldots 1 N 1 N 2 cdots N s 1 1 N s Psi N 1 N 2 ldots 1 N s ldots as displaystyle a s s displaystyle s elektron durumu icin bir olusturma operatorudur as PS N1 N2 Ns 1 N1 N2 Ns 1NsPS N1 N2 1 Ns displaystyle a s Psi N 1 N 2 ldots N s ldots 1 N 1 N 2 cdots N s 1 N s Psi N 1 N 2 ldots 1 N s ldots Notrino durumu Benzer olarak ϕ sϕsbs displaystyle phi sum sigma phi sigma b sigma ϕ displaystyle phi nin tekli notrino dalga fonksiyonu ve ϕs displaystyle phi sigma oldugu yerde yukaridaki gibidir bs displaystyle b sigma su sekilde etki eden s displaystyle sigma durumundaki bir notrinoyu yok eden operatordur bsF M1 M2 Ms 1 M1 M2 Ms 1 1 Ms F M1 M2 1 Ms displaystyle b sigma Phi M 1 M 2 ldots M sigma ldots 1 M 1 M 2 cdots M sigma 1 1 M sigma Phi M 1 M 2 ldots 1 M sigma ldots bs displaystyle b sigma s displaystyle sigma elektron durumu icin bir olusturma operatorudur Agir parcacik durumu r displaystyle rho Heisenberg tarafindan tanitilan daha sonra izospin olarak genellestirildi bir operatordur ve parcacik bir notron oldugunda ozdegeri 1 ve parcacik bir proton ise 1 olan bir agir parcacik durumuna etki eder Bu nedenle agir parcacik durumlari iki sirali sutun vektorleri ile temsil edilecektir burada 10 displaystyle begin pmatrix 1 0 end pmatrix bir notronu temsil eder ve 01 displaystyle begin pmatrix 0 1 end pmatrix bir protonu temsil eder temsil ediliste r displaystyle rho olagan sz displaystyle sigma z spin matrisidir Agir bir parcacigi bir protondan notrona ve tersi yonde degistiren operatorler sirasiyla su sekilde temsil edilir Q sx isy 0100 displaystyle Q sigma x i sigma y begin pmatrix 0 amp 1 0 amp 0 end pmatrix ve Q sx isy 0010 displaystyle Q sigma x i sigma y begin pmatrix 0 amp 0 1 amp 0 end pmatrix un displaystyle u n karsiligi olan vn displaystyle v n n displaystyle n durumunda notronun karsiligi olan proton icin bir eigen fonksiyonudur Hamiltonyen Hamiltonyen uc parcadan olusur ozgur agir parcaciklarin enerjisini temsil eden Hh p displaystyle H text h p ozgur hafif parcaciklarin enerjisini temsil eden Hl p displaystyle H text l p ve Hint displaystyle H text int etkilesimini veren bir parca Hh p 12 1 r N 12 1 r P displaystyle H text h p frac 1 2 1 rho N frac 1 2 1 rho P N displaystyle N ve P displaystyle P sirayla notronun ve protonun operatorleridir Yani eger r 1 displaystyle rho 1 ise Hh p N displaystyle H text h p N dir ve eger r 1 displaystyle rho 1 ise Hh p P displaystyle H text h p P dir Hl p sHsNs sKsMs displaystyle H text l p sum s H s N s sum sigma K sigma M sigma Nukleusun Coulomb alaninda Hs displaystyle H s nin sth displaystyle s text th durumunda elektron enerjisi ve Ns displaystyle N s nin o alandaki elektron sayisi oldugu yerde Ms displaystyle M sigma nin sth displaystyle sigma text th durumundaki notrino sayisi ve Ks displaystyle K sigma nin her bir notrinonun enerjisi oldugu yerde serbest duzlem dalga durumunda oldugu varsayilir Hl p displaystyle H text l p yukaridaki formul ile bulunur Etkilesim kismi bir elektronun ve bir notrinonun simdi bir antinotrino olarak bilinir emisyonu ile birlikte bir protonun bir notrona donusumunu temsil eden bir terim ve ayrica ters islem icin bir terim icermelidir elektron ve proton arasindaki Coulomb kuvveti b displaystyle beta bozunma sureciyle ilgisiz oldugu icin goz ardi edilir Fermi Hint displaystyle H text int icin iki olasi deger onerir ilki spini gormezden gelen bir goreceli olmayan surumu Hint g Qps x ϕ x Q ps x ϕ x displaystyle H text int g left Q psi x phi x Q psi x phi x right ve daha sonra hafif parcaciklarin dort bilesenli oldugunu ancak agir parcaciklarin hizi c displaystyle c ye gorece kucuk ve elektromanyetik vektor potansiyeline benzer etkilesim terimlerinin goz ardi edilebilecegini varsayan bir surum Hint g Qps dps Q ps dps displaystyle H text int g left Q tilde psi delta psi Q tilde psi delta psi right ps displaystyle psi nin ve ϕ displaystyle phi nin artik dort bilesenli Dirac spinorlerinin oldugu ps displaystyle tilde psi nin ps displaystyle psi nin Hermitgen eslenigini temsil ettigi ve d displaystyle delta nin asagidaki matris oldugu yerde yukaridaki formul ile bulunur 0 1001000000100 10 displaystyle begin pmatrix 0 amp 1 amp 0 amp 0 1 amp 0 amp 0 amp 0 0 amp 0 amp 0 amp 1 0 amp 0 amp 1 amp 0 end pmatrix Matris elementleri Sistemin durumu r 1 displaystyle rho pm 1 in agir parcacigin notron mu yoksa proton mu n displaystyle n nin agir parcacigin kuantum durumu Ns displaystyle N s nin s displaystyle s durumundaki elektron sayisi ve Ms displaystyle M sigma nin de s displaystyle sigma durumundaki notrino sayisi oldugu yerder n N1 N2 M1 M2 displaystyle rho n N 1 N 2 ldots M 1 M 2 ldots demeti ile verilir rolativist versiyonunu kullanarak Hint displaystyle H text int Fermi 𝑛 durumunda bir notron bulunan durum ile elektronsuz durum arasindaki matris elemanini verir s displaystyle s durumunda bulunan notrinolar s displaystyle sigma ve bir protonun m displaystyle m durumunda oldugu ve bir elektronun ve bir notrinonun s displaystyle s ve 𝜎 durumlarinda bulundugu durum olarak Hr 1 m Ns 1 Ms 1r 1 n Ns 0 Ms 0 g vm unps sdϕs dt displaystyle H rho 1 m N s 1 M sigma 1 rho 1 n N s 0 M sigma 0 pm g int v m u n tilde psi s delta phi sigma d tau burada integral agir parcaciklarin tum konfigurasyon uzayini kaplar haric r displaystyle rho bu displaystyle pm hafif parcaciklarin toplam sayisinin tek veya cift olmasina gore belirlenir Degisim olasiligi Bilinen gore n displaystyle n durumundaki notronun yasam suresini hesaplamak icin yukaridaki matris elementleri bos elektron ve notrino durumlari uzerinden toplanmalidir Elektron ve notrino pss displaystyle psi s ve ϕs displaystyle phi sigma ozfonksiyonlarinin cekirdek icinde sabit oldugu varsayilarak basitlestirilir yani Compton dalga boylari cekirdegin boyutundan cok daha kucuktur Bu suna yol acar Hr 1 m Ns 1 Ms 1r 1 n Ns 0 Ms 0 gps sdϕs vm undt displaystyle H rho 1 m N s 1 M sigma 1 rho 1 n N s 0 M sigma 0 pm g tilde psi s delta phi sigma int v m u n d tau pss displaystyle psi s ve ϕs displaystyle phi sigma in cekirdegin konumunda degerlendirildigi yerde yukaridaki sekilde bulunur gore daha genis aciklama gerekli bu degisimin olasiligi ar 1 m Ns 1 Ms 1r 1 n Ns 0 Ms 0 2 Hr 1 m Ns 1 Ms 1r 1 n Ns 0 Ms 0 exp 2pih W Hs Ks t 1 W Hs Ks 2 4 Hr 1 m Ns 1 Ms 1r 1 n Ns 0 Ms 0 2 sin2 pth W Hs Ks W Hs Ks 2 displaystyle begin aligned left a rho 1 m N s 1 M sigma 1 rho 1 n N s 0 M sigma 0 right 2 amp left H rho 1 m N s 1 M sigma 1 rho 1 n N s 0 M sigma 0 times frac exp frac 2 pi i h W H s K sigma t 1 W H s K sigma right 2 amp 4 left H rho 1 m N s 1 M sigma 1 rho 1 n N s 0 M sigma 0 right 2 times frac sin 2 left frac pi t h W H s K sigma right W H s K sigma 2 end aligned W displaystyle W nin proton ve notron durumlarinin enerji farklari oldugu yerde yukaridaki sekille bulunur Butun pozitif enerjili notrino spin momentum yonlerinin burada W 1 displaystyle Omega 1 notrino durumlarinin yogunlugudur sonunda sonsuza alinir ortalamasini alarak Hr 1 m Ns 1 Ms 1r 1 n Ns 0 Ms 0 2 avg g24W vm undt 2 ps spss mc2Ksps sbpss displaystyle left langle left H rho 1 m N s 1 M sigma 1 rho 1 n N s 0 M sigma 0 right 2 right rangle text avg frac g 2 4 Omega left int v m u n d tau right 2 left tilde psi s psi s frac mu c 2 K sigma tilde psi s beta psi s right m displaystyle mu in notrinonun kalan kutlesi ve b displaystyle beta nin Dirac matrisi oldugu yerde yukaridaki degeri elde ederiz Bu degismenin olasiliginin W Hs Ks 0 displaystyle W H s K sigma 0 in oldugu ps displaystyle p sigma degerleri icin keskin bir maksimuma sahip olduguna dikkat edilerek bu daha genis aciklama gerekli t8p3g2h4 vm undt 2ps2vs ps spss mc2Ksps sbpss displaystyle t frac 8 pi 3 g 2 h 4 times left int v m u n d tau right 2 frac p sigma 2 v sigma left tilde psi s psi s frac mu c 2 K sigma tilde psi s beta psi s right ps displaystyle p sigma nin ve Ks displaystyle K sigma nin W Hs Ks 0 displaystyle W H s K sigma 0 icin degerleri oldugu yerde yukaridaki degere sadelesir Fermi bu fonksiyon hakkinda uc aciklama yapmistir Notrino durumlari serbest kabul edildiginden Ks gt mc2 displaystyle K sigma gt mu c 2 ve boylece surekli b displaystyle beta spektrumundaki ust limit ise Hs W mc2 displaystyle H s leq W mu c 2 degeridir Hs gt mc2 displaystyle H s gt mc 2 elektronlari icin b displaystyle beta bozunumunun olusmasi icin proton notron enerji farkinin W m m c2 displaystyle W geq m mu c 2 olmasi gerekir Gecis olasiligindakiQmn vm undt displaystyle Q mn int v m u n d tau dd faktoru normalde 1 buyuklugundedir ancak ozel durumlarda yok olur bu b displaystyle beta bozunumu icin yaklasik secim kurallarina yol acar Yasakli degisimler Yukarida da not edildigi gibi ne zaman un displaystyle u n ve vm displaystyle v m agir parcacik durumlari arasindaki Qmn displaystyle Q mn ic carpimi kaybolursa ilgili gecis yasak olur veya daha dogrusu 1 e yakin oldugu durumlardan cok daha az olasidir Cekirdegin protonlarin ve notronlarin bireysel kuantum durumlari acisindan tanimlanmasi iyiyse un displaystyle u n notron durumu ve vm displaystyle v m proton durumu ayni degerde acisal mometuma sahip olmadikca Qmn displaystyle Q mn yok olur aksi durumda tum cekirdegin bozunumdan onceki ve sonraki acisal momentumu kullanilmalidir EtkisiKisa bir sure sonra Fermi nin makalesi yayimlandi Werner Heisenberg un Wolfgang Pauli ye yazdigi bir mektupta cekirdekteki notrinolarin ve elektronlarin yayimlanmasi ve sogurulmasinin karisiklik teorisinin ikinci mertebesinde protonlar ve notronlar arasinda emisyonun nasil olduguna benzer sekilde bir cekime yol acmasi gerektigini ve fotonlarin absorpsiyonu elektromanyetik kuvvete yol actigini kaydetti Kuvvetin Const r5 displaystyle frac text Const r 5 formunda olmasi gerektigini fark etti ancak cagdas deneysel veriler bir milyon kat cok kucuk bir degere yol acti Ayni yilda Hideki Yukawa bu fikre kapildi ancak notrinolar ve elektronlar duragan kutlesi elektrondan yaklasik 200 kat daha agir olan varsayimsal yeni bir parcacik ile degistirildi Sonraki gelismelerFermi nin dortlu fermiyon teorisi zayif etkilesimi oldukca iyi bir sekilde aciklar Maalesef hesaplanan kesit veya etkilesimin olasiligi s GF2E2 displaystyle sigma approx G rm F 2 E 2 enerjisinin karesi olarak buyur Bu kesit sinirsiz buyudugu icin teori yaklasik 100 GeV den cok daha yuksek enerjilerde gecerli degildir Etkilesimin gucunu belirten bir GF Fermi sabiti vardir Bu sonunda dort fermiyon temas etkilesiminin daha eksiksiz bir teoriyle degistirilmesine yol acti elektrozayif teoride aciklandigi gibi bir W veya Z bozonunun degisimi Fermi nin Baglanma Sabiti olan GF altinda birlestirilmis 4 noktali fermiyon vektor akimini gosteren Fermi etkilesimi Fermi nin Teorisi b bozunumu icin olan nukleer bozunumu aciklayan ilk teorik cabadir Etkilesim ayrica muon bozunmasini etkilesimin ayni temel gucune sahip bir muon elektron antinotrino muon notrino ve elektronun birlesmesi yoluyla da aciklayabilir Bu hipotez Gershtein ve Zeldovich tarafindan one suruldu ve Vektor akiminin korunmasi hipotezi olarak da bilinir Orijinal teoride Fermi etkilesimin biciminin iki vektor akiminin temas kuplaji oldugunu varsaydi Daha sonrasinda Lee ve Yang tarafindan eksenel pariteyi ihlal eden bir akimin ortaya cikmasini hicbir seyin engellemedigine dikkat cekildi ve bu Chien Shiung Wu tarafindan yurutulen deneylerle dogrulandi Fermi sabitiFermi sabitinin en kesin deneysel tespiti GF degerinin karesiyle ters orantili olan muon kutlesini W bozonunun kutlesine karsi ihmal ederken muon omrunun olcumleri ile elde edilir Modern terimlerle indirgenmis Fermi sabiti yani dogal birimlerdeki sabit GF0 GF ℏc 3 28g2MW2c4 1 1663787 6 10 5GeV 2 4 5437957 1014J 2 displaystyle G rm F 0 frac G rm F hbar c 3 frac sqrt 2 8 frac g 2 M rm W 2 c 4 1 1663787 6 times 10 5 textrm GeV 2 approx 4 5437957 times 10 14 textrm J 2 degeridir Burada g zayif etkilesimin ciftlenim sabitidir ve MW ise soz konusu bozunmaya aracilik eden W bozonunun kutlesidir Standart Modelde Fermi sabiti Higgs vakum beklenti degeridir v 2GF0 1 2 246 22GeV displaystyle v left sqrt 2 G rm F 0 right 1 2 simeq 246 22 textrm GeV Daha dogrudan yaklasik olarak standart model icin agac duzeyi GF0 pa2 MW2 1 MW2 MZ2 displaystyle G rm F 0 simeq frac pi alpha sqrt 2 M rm W 2 1 M rm W 2 M rm Z 2 Bu W ve Z bozonlari ile MZ MWcos 8W displaystyle M text Z frac M text W cos theta text W arasindaki iliski kullanilarak Weinberg acisi acisindan daha da basitlestirilebilir boylece GF0 pa2 MZ2cos2 8Wsin2 8W displaystyle G rm F 0 simeq frac pi alpha sqrt 2 M rm Z 2 cos 2 theta rm W sin 2 theta rm W Kaynakca Yang 2012 Fermi s b decay Theory Asia Pacific Physics Newsletter 1 1 27 30 doi 10 1142 s2251158x12000045 Theory of Fundamental Processes 1962 Yazar ad1 eksik soyadi1 yardim a b Introduction to Elementary Particles 2nd 2009 ss 314 315 ISBN 978 3 527 40601 2 Yazar ad1 eksik soyadi1 yardim Inward Bound Oxford Oxford University Press 1986 s 418 ISBN 0 19 851997 4 a b Neutrino Oxford University Press 23 Subat 2012 Erisim tarihi 5 Mayis 2017 Yazar ad1 eksik soyadi1 yardim olu kirik baglanti Tentativo di una teoria dei raggi b Italyanca 2 12 1933 Birden fazla yazar name list parameters kullanildi yardim Yazar ad1 eksik soyadi1 yardim Tentativo di una teoria dei raggi b Italyanca 11 1 1 19 1934 doi 10 1007 BF02959820 Birden fazla yazar name list parameters kullanildi yardim Yazar ad1 eksik soyadi1 yardim Versuch einer Theorie der beta Strahlen I Zeitschrift fur Physik Almanca 88 3 4 161 1934 doi 10 1007 BF01351864 Birden fazla yazar name list parameters kullanildi yardim Yazar ad1 eksik soyadi1 yardim a b Fermi s Theory of Beta Decay American Journal of Physics 36 12 1150 1160 1968 doi 10 1119 1 1974382 12 Mayis 2013 tarihinde kaynagindan Erisim tarihi 29 Ocak 2023 Birden fazla yazar name list parameters kullanildi yardim Yazar ad1 eksik soyadi1 yardim Includes complete English translation of Fermi s 1934 paper in German Scientific Correspondence with Bohr Einstein Heisenberg a o Volume II 1930 1939 Springer Verlag Berlin Heidelberg GmbH 1985 Yazar ad1 eksik soyadi1 yardim The Origin of the Concept of Nuclear Forces Institute of Physics Publishing 1996 Yazar ad1 eksik soyadi1 yardim On the interaction of elementary particles I Proceedings of the Physico Mathematical Society of Japan Ingilizce 17 1 1935 Birden fazla yazar name list parameters kullanildi yardim Yazar ad1 eksik soyadi1 yardim The Historical Development of Quantum Theory Volume 6 Part 2 1932 1941 Springer 2001 Yazar ad1 eksik soyadi1 yardim Gerstein 1955 Meson corrections in the theory of beta decay 698 699 Lee 1956 Question of Parity Conservation in Weak Interactions Physical Review 104 1 254 258 doi 10 1103 PhysRev 104 254 Wu 1957 Experimental Test of Parity Conservation in Beta Decay Physical Review 105 4 1413 1415 doi 10 1103 PhysRev 105 1413 MuLan Collaboration 2007 Improved Measurement of the Positive Muon Lifetime and Determination of the Fermi Constant Physical Review Letters 99 3 032001 arXiv 0704 1981 2 doi 10 1103 PhysRevLett 99 032001 PMID 17678280 Birden fazla yazar name list parameters kullanildi yardim Yazar ad1 eksik soyadi1 yardim Yazar eksik soyadi2 yardim The NIST Reference on Constants Units and Uncertainty US National Institute of Standards and Technology June 2015 11 Aralik 2000 tarihinde kaynagindan arsivlendi Erisim tarihi 31 Ekim 2016 Plehn 2005 Quartic Higgs coupling at hadron colliders Physical Review D 72 5 053008 arXiv hep ph 0507321 2 doi 10 1103 PhysRevD 72 053008
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans