Kütleçekimi alanı, ağırlıklı bir kütlenin başka ağırlıklı bir kütle üzerinde oluşturduğu kuvveti açıklamak için kullanılan bir modeldir. Yerçekim alanı, yer çekim mucizesini açıklamak için kullanılır. Birimi newton bölü kilogram (N/kg) ’dır. Orijinal kavramında, yerçekimi noktasal iki ağırlık arasındaki kuvvettir. Newton’u takip ederek Laplace yerçekimi modelini bir çeşit radyasyon alanı olarak tanımladı ve yerçekimi için 19. yüzyılda yapılan açıklamalarda, bir noktasal çekimden çok alan modeli olduğu düşünülmüştür. Bir alan modelinde, iki parçacığın birbirini çekmesinden çok, bu parçacıklar ağırlıklarını yer ve zaman kavramı olarak bozmuştur ve kuvvet olarak ölçülen ve algılanan bu bozulmadır. Yerçekimi kuvveti yoktur veya bu yerçekimi bir uydurma bir kuvvettir.
Klasik mekanik
Fiziksel olarak klasik mekanikte, alan sabit değildir ancak yerçekiminin etkilerini tanımlayan bir modeldir. Bu alana Newton’un evrensel çekim yasası kullanılarak karar verilebilir. Bu yolla karar vermek, M ağırlıklı tek bir parça etrafındaki yer çekim alanı g, vektördeki bütün noktaları içeren direkt olarak noktaya doğru olan bir vektör alanıdır. Her noktadaki alanın büyüklüğü evrensel çekim yasası uygulanarak hesaplandı, uzaydaki herhangi bir nesne üzerindeki noktada kuvvetin birim ağırlığa bölünmesi alanı verir. Bu nedenle, kuvvet alanı korunur. Skaler bir potansiyel enerjisi Φ vardır ve uzaydaki her nokta kuvvet alanı ile ilişkilidir. Bu yerçekimi potansiyeli olarak bilinir. Yerçekim alanı denklemi;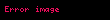

Bu denklem, Gauss yasasının yerçekimi kuramını ve Poisson’ın yerçekimi eşitliğini içerir. Newton ve Gauss yasaları matematiksel eşitliklerdir ve ıraksaklık teoremi ile ilişkilidir. Poisson eşitliğinde bir önceki eşitliğin her iki tarafının da ıraksağını alarak oluşturulur. Bu klasik denklemler, yerçekimi alanı olan bir test parçacığı için, difarensiyel hareket eşitlikleridir. Parçacık çarpımlarının etrafındaki alan her bir parçacığın vektör toplamları kullanılarak hesaplanabilir. Böyle bir alanda kuvvet, her bir alanda hissettiğimiz kuvvetlerin vektör toplamlarına eşittir. Matematiksel olarak;
Ağırlığın üzerindeki yerçekim alanı mj diğer ağırlıklardan mi dolayı oluşan bütün yerçekimi alanlarının mj toplamına eşittir. Birim vektörü 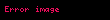
Genel görelilik
Genel görelilikte yerçekim alanı, Einstein'ın alan eşitliğini çözümleyerek bulunabilir,
Ayrıca bakınız
Kaynakça
- ^ Geroch, Robert (1981). General relativity from A to B. University of Chicago Press. s. 181. ISBN . 3 Ocak 2014 tarihinde kaynağından . Erişim tarihi: 24 Aralık 2014., Chapter 7, page 181 3 Ocak 2014 tarihinde Wayback Machine sitesinde .
- ^ Grøn, Øyvind; Hervik, Sigbjørn (2007). Einstein's general theory of relativity: with modern applications in cosmology. Springer Japan. s. 256. ISBN . 8 Mart 2013 tarihinde kaynağından . Erişim tarihi: 24 Aralık 2014., Chapter 10, page 256 18 Haziran 2016 tarihinde Wayback Machine sitesinde .
- ^ J. Foster, J. D. Nightingale, J. Foster, J. D. Nightingale; J. Foster, J. D. Nightingale, J. Foster, J. D. Nightingale (2006). A short course in general relativity. 3. Springer Science & Business. s. 55. ISBN . 3 Ocak 2014 tarihinde kaynağından . Erişim tarihi: 24 Aralık 2014., Chapter 2, page 55 6 Haziran 2016 tarihinde Wayback Machine sitesinde .
- ^ Dynamics and Relativity, J.R. Forshaw, A.G. Smith, Wiley, 2009,
- ^ Encyclopaedia of Physics, R.G. Lerner, G.L. Trigg, 2nd Edition, VHC Publishers, Hans Warlimont, Springer, 2005
- ^ Essential Principles of Physics, P.M. Whelan, M.J. Hodgeson, 2nd Edition, 1978, John Murray,
- ^ Classical Mechanics (2nd Edition), T.W.B. Kibble, European Physics Series, Mc Graw Hill (UK), 1973, .
- ^ Gravitation, J.A. Wheeler, C. Misner, K.S. Thorne, W.H. Freeman & Co, 1973,
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Kutlecekimi alani agirlikli bir kutlenin baska agirlikli bir kutle uzerinde olusturdugu kuvveti aciklamak icin kullanilan bir modeldir Yercekim alani yer cekim mucizesini aciklamak icin kullanilir Birimi newton bolu kilogram N kg dir Orijinal kavraminda yercekimi noktasal iki agirlik arasindaki kuvvettir Newton u takip ederek Laplace yercekimi modelini bir cesit radyasyon alani olarak tanimladi ve yercekimi icin 19 yuzyilda yapilan aciklamalarda bir noktasal cekimden cok alan modeli oldugu dusunulmustur Bir alan modelinde iki parcacigin birbirini cekmesinden cok bu parcaciklar agirliklarini yer ve zaman kavrami olarak bozmustur ve kuvvet olarak olculen ve algilanan bu bozulmadir Yercekimi kuvveti yoktur veya bu yercekimi bir uydurma bir kuvvettir Klasik mekanikFiziksel olarak klasik mekanikte alan sabit degildir ancak yercekiminin etkilerini tanimlayan bir modeldir Bu alana Newton un evrensel cekim yasasi kullanilarak karar verilebilir Bu yolla karar vermek M agirlikli tek bir parca etrafindaki yer cekim alani g vektordeki butun noktalari iceren direkt olarak noktaya dogru olan bir vektor alanidir Her noktadaki alanin buyuklugu evrensel cekim yasasi uygulanarak hesaplandi uzaydaki herhangi bir nesne uzerindeki noktada kuvvetin birim agirliga bolunmesi alani verir Bu nedenle kuvvet alani korunur Skaler bir potansiyel enerjisi F vardir ve uzaydaki her nokta kuvvet alani ile iliskilidir Bu yercekimi potansiyeli olarak bilinir Yercekim alani denklemi g Fm d2Rdt2 GMR R 2 F displaystyle mathbf g frac mathbf F m frac rm d 2 mathbf R rm d t 2 GM frac mathbf hat R mathbf R 2 nabla Phi F yercekimi kuvveti m deneme parcaciginin agirligi R test parcaciginin konumu R displaystyle mathbf hat R R yonunde bir birim vektor t zaman G yercekimi sabiti ve del operatorudur Yercekiminin Newton yasasi yercekimi potensiyeli ve alan ivmesi arasinda bir iliskiyi icerir d2R dt2 ve F m yercekimi ivmesi g ye esittir baslangic ivmesinin esitligi ayni matematiksel formulle yercekimi kuvveti bolu birim agirlik olarak tanimlanabilir Kuvvet yer degistirmeye paralel olmayan bir sekilde uygulandigi icin negatif isaret eklenmistir Alan esitliginde agirligi yazmak yerine agirligi etkileyen yogunlugu r yazabiliriz g 2F 4pGr displaystyle nabla cdot mathbf g nabla 2 Phi 4 pi G rho Bu denklem Gauss yasasinin yercekimi kuramini ve Poisson in yercekimi esitligini icerir Newton ve Gauss yasalari matematiksel esitliklerdir ve iraksaklik teoremi ile iliskilidir Poisson esitliginde bir onceki esitligin her iki tarafinin da iraksagini alarak olusturulur Bu klasik denklemler yercekimi alani olan bir test parcacigi icin difarensiyel hareket esitlikleridir Parcacik carpimlarinin etrafindaki alan her bir parcacigin vektor toplamlari kullanilarak hesaplanabilir Boyle bir alanda kuvvet her bir alanda hissettigimiz kuvvetlerin vektor toplamlarina esittir Matematiksel olarak gj net i jgi 1mj i jFi G i jmiR ij Ri Rj 2 i j Fi displaystyle mathbf g j text net sum i neq j mathbf g i frac 1 m j sum i neq j mathbf F i G sum i neq j m i frac mathbf hat R ij mathbf R i mathbf R j 2 sum i neq j nabla Phi i Agirligin uzerindeki yercekim alani mj diger agirliklardan mi dolayi olusan butun yercekimi alanlarinin mj toplamina esittir Birim vektoru R ij displaystyle mathbf hat R ij ve Ri Rj yonundedir Genel gorelilikGenel gorelilikte yercekim alani Einstein in alan esitligini cozumleyerek bulunabilir G 8pGc4T displaystyle mathbf G frac 8 pi G c 4 mathbf T T G Einstein tensoru ve c isik hizidir Bu denklem Newton un yercekiminin aksine maddenin dagilimina ve uzayin bolgelerindeki enerjiye baglidir Newton un yercekimi yalnizca maddenin dagilimina baglidir Genel gorelilik egimli uzayda bir bolgenin yukariya ivmelenmesine ve alanin izdusumune olan esitligi tanimlar Newton un ikinci yasasina gore uydurma bir kuvvet oldugu deneyimini itiraza neden olacak eger alana gore alinirsa Bunun nedeni insanlarin Dunya uzerinde oturuyorlarken yercekimi kuvveti tarafindan kendilerini asagiya dogru cekiliyormus hissetmeleridir Genellikle yercekim alani genel goreliligin diger etkilerinden farkli olarak klasik mekanikten tahmin edilebilir Fakat kolayca cesitlendirilebilen birkac farklilik vardir ve bunlarin en bilineni herhangi bir alanda isigin esnemesidir Ayrica bakinizMekanik Yercekimi Yercekimi potansiyeli Isaac Newton Potansiyel enerji Kinetik enerji Genel gorelilik testleriKaynakca Geroch Robert 1981 General relativity from A to B University of Chicago Press s 181 ISBN 0 226 28864 1 3 Ocak 2014 tarihinde kaynagindan Erisim tarihi 24 Aralik 2014 Chapter 7 page 181 3 Ocak 2014 tarihinde Wayback Machine sitesinde Gron Oyvind Hervik Sigbjorn 2007 Einstein s general theory of relativity with modern applications in cosmology Springer Japan s 256 ISBN 0 387 69199 5 8 Mart 2013 tarihinde kaynagindan Erisim tarihi 24 Aralik 2014 Chapter 10 page 256 18 Haziran 2016 tarihinde Wayback Machine sitesinde J Foster J D Nightingale J Foster J D Nightingale J Foster J D Nightingale J Foster J D Nightingale 2006 A short course in general relativity 3 Springer Science amp Business s 55 ISBN 0 387 26078 1 3 Ocak 2014 tarihinde kaynagindan Erisim tarihi 24 Aralik 2014 Chapter 2 page 55 6 Haziran 2016 tarihinde Wayback Machine sitesinde Dynamics and Relativity J R Forshaw A G Smith Wiley 2009 ISBN 978 0 470 01460 8 Encyclopaedia of Physics R G Lerner G L Trigg 2nd Edition VHC Publishers Hans Warlimont Springer 2005 Essential Principles of Physics P M Whelan M J Hodgeson 2nd Edition 1978 John Murray ISBN 0 7195 3382 1 Classical Mechanics 2nd Edition T W B Kibble European Physics Series Mc Graw Hill UK 1973 ISBN 0 07 084018 0 Gravitation J A Wheeler C Misner K S Thorne W H Freeman amp Co 1973 ISBN 0 7167 0344 0
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans

