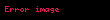Klasik mekanikte momentum ya da devinirlik ( momenta; SI birimi kg·m/s ya da eşdeğer olarak, N·s), bir nesnenin kütlesi ve hızının çarpımıdır; (p = mv). Hız gibi, momentum da vektörel bir niceliktir, yani büyüklüğünün yanı sıra bir yöne de sahiptir. Momentum korunumlu bir niceliktir (çizgisel momentumun korunumu); yani bu, eğer kapalı bir sistem herhangi bir dış kuvvetin etkisi altında değilse, o kapalı sistemin toplam momentumunun değişemeyeceği anlamına gelir. Momentum benzer bir konu olan açısal momentum ile karışmasın diye, bazen çizgisel momentum olarak da anılır.
Her ne kadar Newton'un ikinci yasası şeklinde ifade edilse de, momentumun korunumu Özel görelilik teorisi çerçevesi içinde de geçerlidir ve bazı uygun tanımlarla birlikte, (genelleştirilmiş) bir momentum korunum yasası Elektrodinamik, kuantum mekaniği, kuantum alan teorisi ve genel görelilik teorileri içinde de geçerliliğini korur. Göreli mekanikteki momentum, göreli-olmayan momentumun, fazladan Lorentz faktörü ile çarpılmasıyla elde edilir.
Bir parçacığın çizgisel momentumu

Bir nesne herhangi bir hareket halinde ise, o çerçeve içinde bir momentuma sahiptir. Momentumun çerçeveye bağımlı olduğunu belirtmek önemlidir. Yani aynı nesne, bir gözlem çerçevesinde belli bir momentum değerine sahip olabilirken, başka bir gözlem çerçevesinde ise başka bir momentum değerine sahip olabilir. Örneğin, hareketli bir nesne, yere göre sabit bir noktaya göre seçilen bir gözlem çerçevesinde momentumu olmasına rağmen, kütle merkezine iliştirilen bir gözlem çerçevesinde ise sıfır momentumu vardır.
Bir nesnenin sahip olduğu momentumun miktarı, iki fiziksel büyüklüğe bağlıdır: Kütlesi ve o hızı. Fizikte, momentum için kullanılan sembol genellikle kalın p harfidir (kalın yazılmasının nedeni vektör olmasındandır.); böylece şöyle ifade edilebilir;
burada p momentum, m kütle ve v hızdır.
Örnek: kuzeye doğru yere paralel düz bir rotada 1 m/s hızına ve 1 kg kütleye sahip model bir uçağın momentumu yere göre ölçüldüğünde, kuzey yönünde 1 kg•m/s ‘dir. Kokpitin içindeki bir pilot, kokpit gözlem çerçevesine göre uçağın hızını sıfır ölçeceğinden, momentumunu da sıfır ölçer.
Newton’un ikinci yasasına göre, bir parçacığın momentumunun değişim hızı, parçacık üzerine etki eden net kuvvetle doğru orantılıdır ve yönü ise bu net kuvvetin yönündedir. Net kuvvetin, momentumdan türetilmesi aşağıdaki gibidir.
Eğer kütle zaman içinde sabitse, türevin ikinci terimi (thrust terimi denir) (
Ya da daha basit olarak,
burada F’nin net kuvvet olduğu anlaşılmalıdır.
Örnek: yine bir model uçak, 1 kg kütleli, 1 s içinde kuzeye doğru sıfır hızdan 1 m/s hızına ivmelensin. Bu ivmelenme için gerekli kuvvet 1 newtondur. Momentumdaki değişim 1 kg•m/s’dir. Kokpitteki pilot için ise momentumda bir değişim yoktur. İvmelenme sırasında pilotun sırtının koltuğa yapışması, bu itme'ye tepki kuvvetine karşı dengelenmedir.
Birçok-parçacık sisteminin çizgisel momentumu
Kütle ve hız bağıntıları
Çok-parçacık sisteminin çizgisel momentumu, sistem içindeki ayrı ayrı tüm nesnelerin momentumlarının eşittir.
burada p parçacık sisteminin toplam momentumu, mi vevii’inci nesnenin sırasıyla kütlesi ve hızı ve n ise sistemdeki nesnelerin sayısıdır..
Gösterilebilir ki, herhangi bir sistemin momentumu sıfırdır. Dahası, bu kütle merkezi çerçevesine göre hızı vkm olan başka bir çerçevedeki momentum basitçe aşağıdaki gibidir:
burada:
Bu olarak bilinir.
Kuvvet bağıntısı – Genel hareket denklemleri

Birçok-parçacıklı sistemin çizgisel momentumu, toplam kütle m ile kütle merkezi hızı vkm’nin çarpımı olarak da tanımlanabilir.
Bu özel bir halidir (eğer kütle sabitse).
Tensörler kullanılarak yapılacak daha genel bir türetim için, bir t anında, V hacmini kaplayan, bir S yüzey alanına sahip, 
Tanım gereği stres vektörü 
Gauss'un diverjans teoremini kullanarak, yüzey integrali hacim integraline çevrilirse, (burada 
Artık sadece bu eşitliğin sağ tarafıyla ilgilenebiliriz. Bu noktada dikkat etmemiz gereken, diferansiyel işlemciyi sadece integranda uygulamamaktır. Çünkü bu sürekli ortama sahip gövdenin hareketi esnasında, gövde katı bir cisim olmak zorunda olmadığından, integre ettiğimiz hacim de zaman içinde değişebilir. O halde yukarıdaki integral şu hali alır:
Birinci kısımda türev alınır ve ikinci kısma diverjans teoremi uygulanırsa:
elde edilir.
Artık integralin içindeki ikinci terim şudur: 
Yukarıdaki denklemlerdeki iki integral terimini kolayca tanıyabiliriz. İlk integral hız alanının konvektif türevini ve ikinci integral ise kütlenin zaman içindeki akışını ve değişimini ihtiva eder. Şimdi ise sistemde ne bir kaynak (source) ne de bir gider (sink) olduğunu varsayalım, yani kütle korunuyor olsun, o halde bu ikinci terim sıfırdır. Böylece şunu elde ederiz:
Bunu orijinal denkleme geri koyarsak:
Herhangi bir hacim için integrand sıfır olması gerektiğinden, elde ederiz
Görüldüğü gibi bunu elde etmek için sadece hiçbir kütle kaynağı veya kütle giderinin olmadığını, yani kütlenin korunduğu varsayımını yaptık. O halde bu denklem herhangi bir sürekli sistem için, akışkan sistemlerde dahi geçerlidir. Eğer yalnızca elastic sürekliliği inceliyorsak, konvektif türevin ikinci terimi ihmal edilebilir ve bu durumda bize hız alanının sıradan zaman türevi kalır. Bir sistem dengede ise, ivmesi olmayacağından, momentumunun zamana göre değişimi sıfırdır.
Ya da tensör gösterimiyle,
Bunlar, problemlerini çözmek için kullanılan denge denklemleridir. Mühendislik gösteriminde, denge denklemleri kartezyen koordinatlarda şöyle ifade edilirler:
Çizgisel momentumun korunumu
Çizgisel momentumun korunumu yasası doğanın temel bir yasası olup, eğer kapalı bir sisteme etkiyen hiçbir dış kuvvet mevcut değilse, o kapalı sistemin momentumunun sabit kalacağını söyler. Bu yasanın sonuçlarından bir tanesi ise; herhangi bir nesneler sisteminin kütle merkezi, sistem dışı bir kuvvete maruz kalmadığı sürece, her zaman aynı bir hız ile hareketini sürdürecektir.
Momentumun korunumu, matematiksel bir özellik olan uzayın homojen olmasının bir sonucudur (bir nesnenin uzay içindeki konumu, momentumuna ). O halde momentumun korunduğu bir sistemin içinde fiziksel olarak ne olup bittiği, o sistemin uzaydaki konumunun nerede olduğu ile bir ilgisi bulunmamaktadır.
Analitik mekanikte momentumun korunumu, , ötelemeler altında değişmez kalmasının bir sonucudur. Toplam momentumun olduğu, Lagranjiyene sonsuz küçük bir öteleme yapılıp, bunu ötelenmemiş Lagranjiyenle eşitlenerek ispatlanabilir. Bu Noether teoreminin özel bir halidir.
Kapalı bir sistem için (eğer dış kuvvetler yoksa) toplam momentumun korunumu aslında, Newton'un birinci hareket yasasıdır. Newton'un üçüncü yasası olan, alt sistemler arasında etkiyen kuvvetlerin büyüklükleri aynı ve yönleri zıttır şeklinde ifade edilen, yasası ise momentum korunumunun bir sonucudur.
Uzaydaki konum, vektörel bir nicelik olduğundan, konuma kanonik eşlenik olan momentum da vektörel bir niceliktir-bir yöne sahiptir. O halde, bir silah ateşlendiğinde, sistemin (silah ve merminin) toplam momentumu, bu iki cismin momentumlarının vektörel toplamlarıdır. Ateşlemeden hemen öncesinde silah ve merminin duruyor oldukları farzedilirse (ki bu sistemin başlangıç momentumunun sıfır olmasıdır), sistemin son toplam momentumu da sıfır olmalıdır. Sadece iki nesneye sahip kapalı bir sistemde, nesnelerden birindeki momentum değişimi, diğerinkine büyüklük olarak eşit ve yön olarak ters olmalıdır. Matematiksel olarak,
Momentum, yine kapalı bir sistemde, çarpışmalarda ve iç patlamaların sebep verdiği ayrılmalarda dahi korunur. Kinetik enerji, öte yandan, çarpışmalar esnek değilse, korunmaz. Momentum korunduğundan dolayı, bu bir çarpışma ya da ayrılmayı takip eden durumda bilinmeyen bir hızı, eğer diğer kütle ve hızların bilinmesi durumunda, hesap edilebilir.
Bu gerçeğin gerekli olduğu, fizikte sık rastlanan bir problem, iki parçacığın çarpışmalarıdır. Momentum her zaman korunuyor olacağından, çarpışma öncesi momenta toplamı, çarpışma sonrası momenta toplamına eşit olmalıdır:
Burada; "






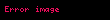
İlk hızlardan, son hızların belirlenmesi (ya da tam tersi), çarpışmanın çeşidine bağlıdır. İki çeşit momentum koruyan çarpışma vardır: Kinetik enerjiyi de koruyan esnek çarpışmalar ve kinetik enerjiyi korumayan esnek olmayan çarpışmalar.
Esnek çarpışmalar
İki bilardo topunun çarpışması, yüksek olmasından dolayı, “neredeyse” tamamen esnek bir çarpışmaya örnek olarak verilebilir. Tamamen esnek olan çarpışmalar sadece teoride, sertlikleri matematiksel olarak sonsuz olan iki cisim arasında var olabilir. İki topun çarpışması esnasında momentumun korunmasının yanı sıra, çarpışma öncesi kinetik enerjilerin toplamı, çarpışma sonraki toplama eşit olmalıdır:
Bir boyutta

Başlangıç hızları bilindiğinde, kafa-kafaya olan çarpışmalardaki son hızlar şöyle verilir:
Birinci cismin kütlesinin diğerinkinden çok daha fazla olduğu durumda (yani, m1 » m2), son hızlar yaklaşık olarak şöyledir:
O halde daha fazla kütleli cisim hızını değiştirmez ve daha az kütleli cisim, diğerinin hızının iki katı kadar daha hızlı ve kendi orijinal hızı kadar daha yavaş hareket eder.
Eşit kütleli iki cismin kafa-kafaya çarpışmasında (yani, m1 = m2), son hızlar şöyle verilir
Yani hızlar basitçe değiş tokuş edilirler. Eğer birinci cisim sıfır olmayan u1 ilk hızına sahip olup ikincisi ise duruyorsa, çarpışmadan sonra birinci cisim duruyor olup, ikincisi u1 son hızı ile hareketine devam edecektir. Bu fenomenin temsili Newton beşiği ile gösterilebilir.

Merkezi esnek çarpışmalarda hareket doğrultusunda bir değişme olmaz. Bu çarpışmalarda kinetik enerji ve momentum korunur. Aşağıdaki iki formül merkezi esnek çarpışma problemlerinde kullanılır:
Çoklu boyutlarda
Birden daha üst boyutlardaki, kafa-kafaya olmayan çarpışmalardaki gibi çarpışmalarda, hız vektörü, çarpışma düzlemine dik ve çarpışma düzlemine paralel olmak üzere, iki bileşenine ayrılır. Çarpışma düzlemine dik hız bileşenleri değişmeden kalırken, çarpışma düzlemindeki hız, bir boyutlu durumdaki gibi hesaplanabilir. Örneğin, iki-boyutlu bir çarpışmada, momenta x ve y bileşenlerine ayrıştırılabilir. Bundan sonra her bileşeni ayrı ayrı hesaplayıp, sonuçları vektörel olarak birleştirip hesaplayabiliriz. Bu vektörün büyüklüğü, kapalı sistemin son momentumudur.
Mükemmel, esnek-olmayan çarpışma
Mükemmel esnek-olmayan çarpışmaya verilen ortak bir örnek, iki kartopunun çarpışıp, akabinde birbirlerine yapışmalarıdır. Bu durumda momentumun korunumu denklemi şöyledir:
Mükemmel, esnek-olmayan çarpışmalar, gösterilebilir ki, kinetik enerjinin maksimum oranda diğer enerji biçimlerine dönüştüğü çarpışmalardır. Örneğin, eğer çarpışmadan sonra iki cisim yapışıp, ortak bir son hız ile hareket ediyorlarsa, daima, nesnelerin hızlarının sıfır olduğu ve böylece kinetik enerjilerinin %1,0’ünün dönüştürüldüğü bir gözlem çerçevesi bulunabilir. Bu göreli durumda dahi doğru olup, parçacık hızlandırıcılarında, kinetik enerjiyi etkin bir biçimde, değişik formlarına çevirmek için, (yani kütleli parçacıklar elde etmek için), kullanılır.
Tazmin katsayısı
Tazmin(restitution) katsayısı, göreli uzaklaşma hızının, göreli yaklaşma hızına oranı olarak tanımlanır. Bir oran olduğundan, boyutsuz bir niceliktir. Tazmin katsayısı, iki çarpışan nesne için, şöyle verilir:
burada
- v1 çarpışmadan sonra, birinci nesnenin son skaler hızı
- v2 çarpışmadan sonra, ikinci nesnenin son skaler hızı
- u1 çarpışmadan önce, birinci nesnenin ilk skaler hızı
- u2 .çarpışmadan önce, ikinci nesnenin ilk skaler hızı.
Mükemmel bir esnek çarpışma, CR ‘nin 1 olduğunu ima eder. Böylece mükemmel esnek çarpışmada, çarpışan cisimlerin göreli yaklaşma ve göreli uzaklaşma hızları eşittir.
Esnek-olmayan çarpışmalar, (CR < 1) eşitsizliğine sahiptirler. Mükemmel bir esnek-olmayan çarpışma durumunda, çarpışan cisimlerin kütle merkezlerine göre hızları sıfırdır. Böylece cisimler, çarpışmadan sonra birbirlerine yapışırlar.
Patlamalar
Patlamalar, bir zincirleme reaksiyon sonucunda, potansiyel enerjinin kinetik enerjiye dönüşmesiyle çevrede bulunan materyallerin yer değiştirmesi şeklinde oluşurlar. Patlamalar potansiyel enerjiyi korumaz. Bunun yerine kimyasal, mekanik ya da nükleer biçimlerinde bulunan potansiyel enerjiyi, kinetik enerji, akustik enerji ve elektromagnetik ışınım biçimlerine çevirir.
Momentumun çağdaş tanımları
Göreli mekanikte momentum
Göreli mekanikte, korunabilmesi için, momentum şöyle tanımlanmalıdır
burada m0 cismin değişmez kütle si ve ϒ
İle verilen burada v cismin hızı ve c ışık hızıdır. Tersine bağıntı şöyle verilir:
Burada 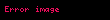
Göreli momentum, değişmez kütle ile cismin çarpımı olarak da verilir. Cismin has hızı, cismin, gözlemcinin kendi gözlem çerçevesinde ölçtüğü konumunun, cismin kendi üzerinden geçen zamana göre(yani cismin göre) olan değişim hızıdır. Klasik mekaniğin geçerli olduğu bölgede, göreli momentum, Newtonsal momentuma yakınsar: düşük hızlarda, γm0v, yaklaşık olarak m0v Newtonsal momentum ifadesine eşittir.

Bir cismin toplam E enerjisi, göreli momentumu ile şöyle ilintilidir
burada p, p’nin büyüklüğüdür. Bu göreli enerji-momentum bağıntısı, foton gibi kütlesiz parçacıklar için bile geçerlidir; m0 = 0 seçilirse
olur. Hem kütleli hem de kütlesiz parçacıklar için de, göreli momentum, λ’ya şöyle bağlıdır.
burada h, Planck sabitidir.
Dörtlü vektör formülasyonu
Göreli , Lorentz ötelemeleri altında değişmez kalmalarından dolayı, Albert Einstein tarafından önerilmiş tir. Dörtlü-momentum P şöyle tanımlanır:
burada E = γm0c2,sistemin toplam göreli enerjisi ve px, py ve pz sırasıyla göreli momentumun x-, y- ve z bileşenlerini temsil eder.
Momentum dörtlü vektörünün büyüklüğü || P ||, m0c’ye eşittir, çünkü
dir ve her gözlem çerçevesi için değişmezdir. Kapalı bir sistemde, toplam dörtlü momentum korunur ki bu en nihayetinde hem enerjinin hem de momentumun korunumunu birleştirip, bir tek denkleme indirgemiş olur. Örneğin, in the radiationless collision of two particles with rest masses 
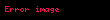




burada
Esnek çarpışmalarda, durgun kütle değişmez iken (

Genelleştirilmiş momentum
Momentum, öteleme invaryansının . Öyle ki, sadece parçacıklar değil, alanlar ve diğer her şey momentuma sahip olabilir. Ancak uzay-zamanın olduğu yerlerde, öteleme invaryansı için hiçbir Noether yükü yoktur.
Kuantum mekaniğinde momentum
Kuantum mekaniğinde, momentum, dalga fonksiyonu üzerine etkiyen bir olarak tanımlanır. Heisenberg belirsizlik ilkesi, bir sistemin aynı anda hem konumunu hem de momentumunu ne kadar hassas olarak belirleyebileceğimizin sınırların tanımlar. Kuantum mekaniğinde, konum ve momentum,
Konum tabanında tasvir edilen bir parçacığın momentum işlemcisi şöyledir;
burada ∇ işlemcisi, ħ indirgenmiş Planck sabiti ve i sanal birimdir. Bu momentum işlemcisinin çokça kullanılan şeklidir, ancak değişik başka tabanlarda değişik biçimler alabilir. Örneğin momentum tabanında, momentum işlemcisi şöyle temsil edilir
burada ψ(p) dalga fonksiyonuna etkiyen işlemci p, dalga fonksiyonu kere p değeri sonucunu verir. Bu aynı konum işlemcisinin dalga fonksiyonuna etkidikten sonra, konum değeri x çarpı dalga fonksiyonunu vermesi gibidir.
Elektromagnetizmada momentum
Elektrik ve magnetik alanlar, durağan ya da zaman içinde değişip değişmediklerine bakılmaksızın, momentum taşırlar. Bir metal küre, silindirsel kapasitör veya mıknatıs bir çubuğun üzerindeki elektrostatik(magnetostatik) alanın P basıncı aşağıdaki gibidir.
burada 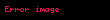

Işık (görülür, UV, radyo) elektromagnetik bir dalgadır ve böylece momentuma sahiptir. Fotonun kütlesi olmamasına rağmen yine de momentum taşır. Bu özellik güneş yelkeni gibi uygulamalara zemin hazırlar. Dielektrik ortamdaki ışığın momentumunun hesaplanması tartışmalıdır (Bkz [1]3 Ocak 2012 tarihinde Wayback Machine sitesinde .).) Momentum, elektrodinamik bir sistemde korunur(alandaki momentumdan, hareket eden bölümlerin mekanik momentumuna dönüşebilir). Bir alanın momentumunun hesabı, genellikle ve belli bir hacim üzerinden integre edilmiş Poynting vektörünün zaman içindeki değişimleri dikkate alınarak yapılır. Bu ise bileşenleri enerji yoğunluğu ve momentum yoğunluğu olan bir tensör alanıdır. Elektromagnetik etkileşmeler söz konusu olduğunda, kanonik momentuma karşılık gelen kuantum mekaniksel momentum işlemcisi
Yerine,
,
ile ifade edilir. Burada:
elektromagnetik vektör potansiyeli
yüklü parçacığın kütlesi
hızı
yüküdür.
Açısal momentum
Açısal momentum çember şeklinde bir düzlemde dönen bir cismin sahip olduğu bir özelliktir. Momentum gibi sabittir:

r : Parçacığın seçilen orijin noktasına göre uzaklık vektörü
p : Parçacığın momentumu
Kaynakça
- , David (1960-2007). Fundamentals of Physics. John Wiley & Sons. Chapter 9.
- Serway, Raymond; Jewett, John (2003). Physics for Scientists and Engineers (6 ed.). Brooks Cole.
- Stenger, Victor J. (2000). Timeless Reality: Symmetry, Simplicity, and Multiple Universes. Prometheus Books. Chpt. 12 in particular.
- Tipler, Paul (1998). Physics for Scientists and Engineers: Vol. 1: Mechanics, Oscillations and Waves, Thermodynamics (4th ed.). W. H. Freeman.
- Hand, Louis N.; Finch, Janet D. (1998). Analytical Mechanics. Cambridge University Press. Chapter 4.
- Dorn Bader Physik Gymnasium Gesamtband, Sek 2,, 2000 Scroedel Verlag,
- Metzler Physik J. Grehn, J.Kause, 4. Basim,
Notlar
- ^ "TDK Bilim ve Sanat Terimleri Ana Sözlüğü". Erişim tarihi: 18 Nisan 2011. []
- ^ . 30 Mart 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 16 Nisan 2011.
- ^ McGill & King (1995). Engineering Mechanics, An Introduction to Dynamics (3 bas.). PWS Publishing Company. .
- ^ Hand, Louis N.; Finch, Janet D. (1998). Analytical Mechanics. Cambridge University Press. Chapter 4.
- ^ Pike, Edward Roy; Sabatier, Pierre Celestin (2002). Scattering. Academic Press. s. 703. ISBN ., Chpater 2.1.3, page 703
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Klasik mekanikte momentum ya da devinirlik momenta SI birimi kg m s ya da esdeger olarak N s bir nesnenin kutlesi ve hizinin carpimidir p mv Hiz gibi momentum da vektorel bir niceliktir yani buyuklugunun yani sira bir yone de sahiptir Momentum korunumlu bir niceliktir cizgisel momentumun korunumu yani bu eger kapali bir sistem herhangi bir dis kuvvetin etkisi altinda degilse o kapali sistemin toplam momentumunun degisemeyecegi anlamina gelir Momentum benzer bir konu olan acisal momentum ile karismasin diye bazen cizgisel momentum olarak da anilir Her ne kadar Newton un ikinci yasasi seklinde ifade edilse de momentumun korunumu Ozel gorelilik teorisi cercevesi icinde de gecerlidir ve bazi uygun tanimlarla birlikte genellestirilmis bir momentum korunum yasasi Elektrodinamik kuantum mekanigi kuantum alan teorisi ve genel gorelilik teorileri icinde de gecerliligini korur Goreli mekanikteki momentum goreli olmayan momentumun fazladan Lorentz faktoru ile carpilmasiyla elde edilir Bir parcacigin cizgisel momentumuEinstein in asansorundeki Newton un elmasi A kisisinin gozlem cercevesinde elma sifir olmayan bir hiza ve momentuma sahiptir Asansorun ve B kisisinin gozlem cercevesinde ise elma sifir bir hiza ve momentuma sahiptir Bir nesne herhangi bir hareket halinde ise o cerceve icinde bir momentuma sahiptir Momentumun cerceveye bagimli oldugunu belirtmek onemlidir Yani ayni nesne bir gozlem cercevesinde belli bir momentum degerine sahip olabilirken baska bir gozlem cercevesinde ise baska bir momentum degerine sahip olabilir Ornegin hareketli bir nesne yere gore sabit bir noktaya gore secilen bir gozlem cercevesinde momentumu olmasina ragmen kutle merkezine ilistirilen bir gozlem cercevesinde ise sifir momentumu vardir Bir nesnenin sahip oldugu momentumun miktari iki fiziksel buyukluge baglidir Kutlesi ve o hizi Fizikte momentum icin kullanilan sembol genellikle kalin p harfidir kalin yazilmasinin nedeni vektor olmasindandir boylece soyle ifade edilebilir p mv displaystyle mathbf p m mathbf v burada p momentum m kutle ve v hizdir Ornek kuzeye dogru yere paralel duz bir rotada 1 m s hizina ve 1 kg kutleye sahip model bir ucagin momentumu yere gore olculdugunde kuzey yonunde 1 kg m s dir Kokpitin icindeki bir pilot kokpit gozlem cercevesine gore ucagin hizini sifir olceceginden momentumunu da sifir olcer Newton un ikinci yasasina gore bir parcacigin momentumunun degisim hizi parcacik uzerine etki eden net kuvvetle dogru orantilidir ve yonu ise bu net kuvvetin yonundedir Net kuvvetin momentumdan turetilmesi asagidaki gibidir F dpdt mdvdt vdmdt displaystyle sum mathbf F mathrm d mathbf p over mathrm d t m mathrm d mathbf v over mathrm d t mathbf v mathrm d m over mathrm d t Eger kutle zaman icinde sabitse turevin ikinci terimi thrust terimi denir vdmdt 0 displaystyle scriptstyle mathbf v mathrm d m over mathrm d t 0 Boylece sunu yazabiliriz F ma displaystyle sum mathbf F m mathbf a Ya da daha basit olarak F ma displaystyle mathbf F m mathbf a burada F nin net kuvvet oldugu anlasilmalidir Ornek yine bir model ucak 1 kg kutleli 1 s icinde kuzeye dogru sifir hizdan 1 m s hizina ivmelensin Bu ivmelenme icin gerekli kuvvet 1 newtondur Momentumdaki degisim 1 kg m s dir Kokpitteki pilot icin ise momentumda bir degisim yoktur Ivmelenme sirasinda pilotun sirtinin koltuga yapismasi bu itme ye tepki kuvvetine karsi dengelenmedir Bircok parcacik sisteminin cizgisel momentumuKutle ve hiz bagintilari Cok parcacik sisteminin cizgisel momentumu sistem icindeki ayri ayri tum nesnelerin momentumlarinin esittir p i 1nmivi m1v1 m2v2 m3v3 mnvn displaystyle mathbf p sum i 1 n m i mathbf v i m 1 mathbf v 1 m 2 mathbf v 2 m 3 mathbf v 3 cdots m n mathbf v n burada p parcacik sisteminin toplam momentumu mi vevii inci nesnenin sirasiyla kutlesi ve hizi ve n ise sistemdeki nesnelerin sayisidir Gosterilebilir ki herhangi bir sistemin momentumu sifirdir Dahasi bu kutle merkezi cercevesine gore hizi vkm olan baska bir cercevedeki momentum basitce asagidaki gibidir p mvkm displaystyle mathbf p m mathbf v text km burada m i 1nmi displaystyle m sum i 1 n m i Bu olarak bilinir Kuvvet bagintisi Genel hareket denklemleri Maddesel bir govdenin hareketi Bircok parcacikli sistemin cizgisel momentumu toplam kutle m ile kutle merkezi hizi vkm nin carpimi olarak da tanimlanabilir F dpdt mdvkmdt makm displaystyle sum mathbf F mathrm d mathbf p over mathrm d t m frac mathrm d mathbf v km mathrm d t m mathbf a km Bu ozel bir halidir eger kutle sabitse Tensorler kullanilarak yapilacak daha genel bir turetim icin bir t aninda V hacmini kaplayan bir S yuzey alanina sahip Ti n displaystyle scriptstyle T i n ile temsil edilen birim yuzey alani basina yuzey kuvvetinin ettigi V hacmi icinde her noktadaki birim hacim basina olan Fi govde kuvvetinin etkidigi cismin govdesi boyunca belirlenmis vi hiz alani ile belirlenmis oldugu varsayilan hareket halindeki bir cismi dusunelim sekle bakin STi n dS VFidV ddt VrvidV displaystyle int S T i n dS int V F i dV frac d dt int V rho v i dV Tanim geregi stres vektoru Ti n sijnj displaystyle scriptstyle T i n equiv sigma ij n j dir o halde SsijnjdS VFidV ddt VrvidV displaystyle int S sigma ij n j dS int V F i dV frac d dt int V rho v i dV Gauss un diverjans teoremini kullanarak yuzey integrali hacim integraline cevrilirse burada j xj displaystyle scriptstyle partial j equiv frac partial partial x j ile diferansiyel islemci belirtilmektedir bu bize sunu verir V jsijdV VFidV ddt VrvidV displaystyle int V partial j sigma ij dV int V F i dV frac d dt int V rho v i dV Artik sadece bu esitligin sag tarafiyla ilgilenebiliriz Bu noktada dikkat etmemiz gereken diferansiyel islemciyi sadece integranda uygulamamaktir Cunku bu surekli ortama sahip govdenin hareketi esnasinda govde kati bir cisim olmak zorunda olmadigindan integre ettigimiz hacim de zaman icinde degisebilir O halde yukaridaki integral su hali alir ddt rvidV rvi tdV rvivknkdA displaystyle frac d dt int rho v i dV int frac partial rho v i partial t dV oint rho v i v k n k dA Birinci kisimda turev alinir ve ikinci kisma diverjans teoremi uygulanirsa ddt rvidV r vi t vi r t k rvivk dV displaystyle frac d dt int rho v i dV int left left rho frac partial v i partial t v i frac partial rho partial t right partial k rho v i v k right dV elde edilir Artik integralin icindeki ikinci terim sudur k rvivk rvk kvi vi k rvk displaystyle partial k rho v i v k rho v k cdot partial k v i v i partial k rho v k Bunu onceki denklemde yerine koyup terimleri duzenledikten sonra sunu elde ederiz ddt rvidV r t vk k vidV r t k rvk vidV displaystyle frac d dt int rho v i dV int rho left frac partial partial t v k partial k right v i dV int left frac partial rho partial t partial k rho v k right v i dV Yukaridaki denklemlerdeki iki integral terimini kolayca taniyabiliriz Ilk integral hiz alaninin konvektif turevini ve ikinci integral ise kutlenin zaman icindeki akisini ve degisimini ihtiva eder Simdi ise sistemde ne bir kaynak source ne de bir gider sink oldugunu varsayalim yani kutle korunuyor olsun o halde bu ikinci terim sifirdir Boylece sunu elde ederiz ddt rvidV rDviDtdV displaystyle frac d dt int rho v i dV int rho frac Dv i Dt dV Bunu orijinal denkleme geri koyarsak V jsij Fi rDviDt dV 0 displaystyle int V left partial j sigma ij F i rho frac Dv i Dt right dV 0 Herhangi bir hacim icin integrand sifir olmasi gerektiginden elde ederiz jsij Fi rDviDt displaystyle partial j sigma ij F i rho frac Dv i Dt Goruldugu gibi bunu elde etmek icin sadece hicbir kutle kaynagi veya kutle giderinin olmadigini yani kutlenin korundugu varsayimini yaptik O halde bu denklem herhangi bir surekli sistem icin akiskan sistemlerde dahi gecerlidir Eger yalnizca elastic surekliligi inceliyorsak konvektif turevin ikinci terimi ihmal edilebilir ve bu durumda bize hiz alaninin siradan zaman turevi kalir Bir sistem dengede ise ivmesi olmayacagindan momentumunun zamana gore degisimi sifirdir F dpdt macm 0 displaystyle sum mathbf F mathrm d mathbf p over mathrm d t m mathbf a cm 0 Ya da tensor gosterimiyle jsij Fi 0 displaystyle partial j sigma ij F i 0 Bunlar problemlerini cozmek icin kullanilan denge denklemleridir Muhendislik gosteriminde denge denklemleri kartezyen koordinatlarda soyle ifade edilirler sx x tyx y tzx z Fx 0 displaystyle frac partial sigma x partial x frac partial tau yx partial y frac partial tau zx partial z F x 0 txy x sy y tzy z Fy 0 displaystyle frac partial tau xy partial x frac partial sigma y partial y frac partial tau zy partial z F y 0 txz x tyz y sz z Fz 0 displaystyle frac partial tau xz partial x frac partial tau yz partial y frac partial sigma z partial z F z 0 Cizgisel momentumun korunumuCizgisel momentumun korunumu yasasi doganin temel bir yasasi olup eger kapali bir sisteme etkiyen hicbir dis kuvvet mevcut degilse o kapali sistemin momentumunun sabit kalacagini soyler Bu yasanin sonuclarindan bir tanesi ise herhangi bir nesneler sisteminin kutle merkezi sistem disi bir kuvvete maruz kalmadigi surece her zaman ayni bir hiz ile hareketini surdurecektir Momentumun korunumu matematiksel bir ozellik olan uzayin homojen olmasinin bir sonucudur bir nesnenin uzay icindeki konumu momentumuna O halde momentumun korundugu bir sistemin icinde fiziksel olarak ne olup bittigi o sistemin uzaydaki konumunun nerede oldugu ile bir ilgisi bulunmamaktadir Analitik mekanikte momentumun korunumu otelemeler altinda degismez kalmasinin bir sonucudur Toplam momentumun oldugu Lagranjiyene sonsuz kucuk bir oteleme yapilip bunu otelenmemis Lagranjiyenle esitlenerek ispatlanabilir Bu Noether teoreminin ozel bir halidir Kapali bir sistem icin eger dis kuvvetler yoksa toplam momentumun korunumu aslinda Newton un birinci hareket yasasidir Newton un ucuncu yasasi olan alt sistemler arasinda etkiyen kuvvetlerin buyuklukleri ayni ve yonleri zittir seklinde ifade edilen yasasi ise momentum korunumunun bir sonucudur Uzaydaki konum vektorel bir nicelik oldugundan konuma kanonik eslenik olan momentum da vektorel bir niceliktir bir yone sahiptir O halde bir silah ateslendiginde sistemin silah ve merminin toplam momentumu bu iki cismin momentumlarinin vektorel toplamlaridir Ateslemeden hemen oncesinde silah ve merminin duruyor olduklari farzedilirse ki bu sistemin baslangic momentumunun sifir olmasidir sistemin son toplam momentumu da sifir olmalidir Sadece iki nesneye sahip kapali bir sistemde nesnelerden birindeki momentum degisimi digerinkine buyukluk olarak esit ve yon olarak ters olmalidir Matematiksel olarak Dp1 Dp2 displaystyle Delta mathbf p 1 Delta mathbf p 2 Momentum yine kapali bir sistemde carpismalarda ve ic patlamalarin sebep verdigi ayrilmalarda dahi korunur Kinetik enerji ote yandan carpismalar esnek degilse korunmaz Momentum korundugundan dolayi bu bir carpisma ya da ayrilmayi takip eden durumda bilinmeyen bir hizi eger diger kutle ve hizlarin bilinmesi durumunda hesap edilebilir Bu gercegin gerekli oldugu fizikte sik rastlanan bir problem iki parcacigin carpismalaridir Momentum her zaman korunuyor olacagindan carpisma oncesi momenta toplami carpisma sonrasi momenta toplamina esit olmalidir m1u1 m2u2 m1v1 m2v2 displaystyle m 1 mathbf u 1 m 2 mathbf u 2 m 1 mathbf v 1 m 2 mathbf v 2 Burada u1 displaystyle mathbf u 1 ve u2 displaystyle mathbf u 2 Carpisma oncesi hizlar metresaniye displaystyle frac metre saniye biriminde v1 displaystyle mathbf v 1 ve v2 displaystyle mathbf v 2 Carpisma sonrasi hizlar metresaniye displaystyle frac metre saniye biriminde m displaystyle m Kutle kg displaystyle kg biriminde Ilk hizlardan son hizlarin belirlenmesi ya da tam tersi carpismanin cesidine baglidir Iki cesit momentum koruyan carpisma vardir Kinetik enerjiyi de koruyan esnek carpismalar ve kinetik enerjiyi korumayan esnek olmayan carpismalar Esnek carpismalar Iki bilardo topunun carpismasi yuksek olmasindan dolayi neredeyse tamamen esnek bir carpismaya ornek olarak verilebilir Tamamen esnek olan carpismalar sadece teoride sertlikleri matematiksel olarak sonsuz olan iki cisim arasinda var olabilir Iki topun carpismasi esnasinda momentumun korunmasinin yani sira carpisma oncesi kinetik enerjilerin toplami carpisma sonraki toplama esit olmalidir 12m1u12 12m2u22 12m1v12 12m2v22 displaystyle tfrac 1 2 m 1 u 1 2 tfrac 1 2 m 2 u 2 2 tfrac 1 2 m 1 v 1 2 tfrac 1 2 m 2 v 2 2 Bir boyutta Bir Newton besigi momentum korunumunu gosteriyor Baslangic hizlari bilindiginde kafa kafaya olan carpismalardaki son hizlar soyle verilir v1 m1 m2m1 m2 u1 2m2m1 m2 u2 displaystyle mathbf v 1 left frac m 1 m 2 m 1 m 2 right mathbf u 1 left frac 2m 2 m 1 m 2 right mathbf u 2 v2 m2 m1m1 m2 u2 2m1m1 m2 u1 displaystyle mathbf v 2 left frac m 2 m 1 m 1 m 2 right mathbf u 2 left frac 2m 1 m 1 m 2 right mathbf u 1 Birinci cismin kutlesinin digerinkinden cok daha fazla oldugu durumda yani m1 m2 son hizlar yaklasik olarak soyledir v1 u1 displaystyle mathbf v 1 mathbf u 1 v2 2u1 u2 displaystyle mathbf v 2 2 mathbf u 1 mathbf u 2 O halde daha fazla kutleli cisim hizini degistirmez ve daha az kutleli cisim digerinin hizinin iki kati kadar daha hizli ve kendi orijinal hizi kadar daha yavas hareket eder Esit kutleli iki cismin kafa kafaya carpismasinda yani m1 m2 son hizlar soyle verilir v1 u2 displaystyle mathbf v 1 mathbf u 2 v2 u1 displaystyle mathbf v 2 mathbf u 1 Yani hizlar basitce degis tokus edilirler Eger birinci cisim sifir olmayan u1 ilk hizina sahip olup ikincisi ise duruyorsa carpismadan sonra birinci cisim duruyor olup ikincisi u1 son hizi ile hareketine devam edecektir Bu fenomenin temsili Newton besigi ile gosterilebilir ORNEK Ilk hizlari ve kutleleri m1 1000kg u1 5m s m 0 1kg u2 0m s Son hizlari yaklasik olarak verilmistir v1 4 999m s v2 9 999m s Merkezi esnek carpismalarda hareket dogrultusunda bir degisme olmaz Bu carpismalarda kinetik enerji ve momentum korunur Asagidaki iki formul merkezi esnek carpisma problemlerinde kullanilir P 1 ilk P 2 ilk P 1 son P 2 son displaystyle overrightarrow P text 1 ilk overrightarrow P text 2 ilk overrightarrow P text 1 son overrightarrow P text 2 son Coklu boyutlarda Birden daha ust boyutlardaki kafa kafaya olmayan carpismalardaki gibi carpismalarda hiz vektoru carpisma duzlemine dik ve carpisma duzlemine paralel olmak uzere iki bilesenine ayrilir Carpisma duzlemine dik hiz bilesenleri degismeden kalirken carpisma duzlemindeki hiz bir boyutlu durumdaki gibi hesaplanabilir Ornegin iki boyutlu bir carpismada momenta x ve y bilesenlerine ayristirilabilir Bundan sonra her bileseni ayri ayri hesaplayip sonuclari vektorel olarak birlestirip hesaplayabiliriz Bu vektorun buyuklugu kapali sistemin son momentumudur Mukemmel esnek olmayan carpisma Mukemmel esnek olmayan carpismaya verilen ortak bir ornek iki kartopunun carpisip akabinde birbirlerine yapismalaridir Bu durumda momentumun korunumu denklemi soyledir m1u1 m2u2 m1 m2 v displaystyle m 1 mathbf u 1 m 2 mathbf u 2 left m 1 m 2 right mathbf v dd Mukemmel esnek olmayan carpismalar gosterilebilir ki kinetik enerjinin maksimum oranda diger enerji bicimlerine donustugu carpismalardir Ornegin eger carpismadan sonra iki cisim yapisip ortak bir son hiz ile hareket ediyorlarsa daima nesnelerin hizlarinin sifir oldugu ve boylece kinetik enerjilerinin 1 0 unun donusturuldugu bir gozlem cercevesi bulunabilir Bu goreli durumda dahi dogru olup parcacik hizlandiricilarinda kinetik enerjiyi etkin bir bicimde degisik formlarina cevirmek icin yani kutleli parcaciklar elde etmek icin kullanilir Tazmin katsayisi Tazmin restitution katsayisi goreli uzaklasma hizinin goreli yaklasma hizina orani olarak tanimlanir Bir oran oldugundan boyutsuz bir niceliktir Tazmin katsayisi iki carpisan nesne icin soyle verilir CR v2 v1u1 u2 displaystyle C R frac v 2 v 1 u 1 u 2 burada v1 carpismadan sonra birinci nesnenin son skaler hizi v2 carpismadan sonra ikinci nesnenin son skaler hizi u1 carpismadan once birinci nesnenin ilk skaler hizi u2 carpismadan once ikinci nesnenin ilk skaler hizi Mukemmel bir esnek carpisma CR nin 1 oldugunu ima eder Boylece mukemmel esnek carpismada carpisan cisimlerin goreli yaklasma ve goreli uzaklasma hizlari esittir Esnek olmayan carpismalar CR lt 1 esitsizligine sahiptirler Mukemmel bir esnek olmayan carpisma durumunda carpisan cisimlerin kutle merkezlerine gore hizlari sifirdir Boylece cisimler carpismadan sonra birbirlerine yapisirlar Patlamalar Patlamalar bir zincirleme reaksiyon sonucunda potansiyel enerjinin kinetik enerjiye donusmesiyle cevrede bulunan materyallerin yer degistirmesi seklinde olusurlar Patlamalar potansiyel enerjiyi korumaz Bunun yerine kimyasal mekanik ya da nukleer bicimlerinde bulunan potansiyel enerjiyi kinetik enerji akustik enerji ve elektromagnetik isinim bicimlerine cevirir Momentumun cagdas tanimlariGoreli mekanikte momentum Goreli mekanikte korunabilmesi icin momentum soyle tanimlanmalidir p gm0v displaystyle mathbf p gamma m 0 mathbf v burada m0 cismin degismez kutle si ve ϒ g 11 v c 2 displaystyle gamma frac 1 sqrt 1 v c 2 Ile verilen burada v cismin hizi ve c isik hizidir Tersine baginti soyle verilir v c2p pc 2 m0c2 2 c2pE displaystyle mathbf v frac c 2 mathbf p sqrt pc 2 m 0 c 2 2 frac c 2 mathbf p E Burada p px2 py2 pz2 displaystyle p sqrt p x 2 p y 2 p z 2 momentumun buyuklugudur Goreli momentum degismez kutle ile cismin carpimi olarak da verilir Cismin has hizi cismin gozlemcinin kendi gozlem cercevesinde olctugu konumunun cismin kendi uzerinden gecen zamana gore yani cismin gore olan degisim hizidir Klasik mekanigin gecerli oldugu bolgede goreli momentum Newtonsal momentuma yakinsar dusuk hizlarda gm0v yaklasik olarak m0v Newtonsal momentum ifadesine esittir E goreli enerjisi m0 kutlesi p goreli momentumu ve m gm0 goreli kutlesinin grafiksel bir temsili Bir cismin toplam E enerjisi goreli momentumu ile soyle ilintilidir E2 pc 2 m0c2 2 displaystyle E 2 pc 2 m 0 c 2 2 burada p p nin buyuklugudur Bu goreli enerji momentum bagintisi foton gibi kutlesiz parcaciklar icin bile gecerlidir m0 0 secilirse E pc displaystyle E pc olur Hem kutleli hem de kutlesiz parcaciklar icin de goreli momentum l ya soyle baglidir p h l displaystyle p h lambda burada h Planck sabitidir Dortlu vektor formulasyonu Goreli Lorentz otelemeleri altinda degismez kalmalarindan dolayi Albert Einstein tarafindan onerilmis tir Dortlu momentum P soyle tanimlanir P E c px py pz displaystyle mathbf P E c p x p y p z burada E gm0c2 sistemin toplam goreli enerjisi ve px py ve pz sirasiyla goreli momentumun x y ve z bilesenlerini temsil eder Momentum dortlu vektorunun buyuklugu P m0c ye esittir cunku P 2 E c 2 p2 m0c 2 displaystyle mathbf P 2 E c 2 p 2 m 0 c 2 dir ve her gozlem cercevesi icin degismezdir Kapali bir sistemde toplam dortlu momentum korunur ki bu en nihayetinde hem enerjinin hem de momentumun korunumunu birlestirip bir tek denkleme indirgemis olur Ornegin in the radiationless collision of two particles with rest masses m1 displaystyle m 1 ve m2 displaystyle m 2 kutleli v1 displaystyle mathbf v 1 vev2 displaystyle mathbf v 2 ilk hizlarina sahip goreli iki parcacigin isimasiz carpismalarindaki v3 displaystyle mathbf v 3 ve v4 displaystyle mathbf v 4 son hizlari dortlu momentumun korunumundan asagidaki gibi bulunabilir P1 P2 P3 P4 displaystyle mathbf P 1 mathbf P 2 mathbf P 3 mathbf P 4 burada Pi migi c vi displaystyle mathbf P i m i gamma i c mathbf v i Esnek carpismalarda durgun kutle degismez iken m1 m3 displaystyle m 1 m 3 and m2 m4 displaystyle m 2 m 4 esnek olmayan carpismalarda durgun kutlelerde degisiklik olur Dortlu momentumun korunumunun uzay zamanin homojen olmasinin bir sonucu oldugu ispatlanabilir Genellestirilmis momentum Momentum oteleme invaryansinin Oyle ki sadece parcaciklar degil alanlar ve diger her sey momentuma sahip olabilir Ancak uzay zamanin oldugu yerlerde oteleme invaryansi icin hicbir Noether yuku yoktur Kuantum mekaniginde momentum Kuantum mekaniginde momentum dalga fonksiyonu uzerine etkiyen bir olarak tanimlanir Heisenberg belirsizlik ilkesi bir sistemin ayni anda hem konumunu hem de momentumunu ne kadar hassas olarak belirleyebilecegimizin sinirlarin tanimlar Kuantum mekaniginde konum ve momentum Konum tabaninda tasvir edilen bir parcacigin momentum islemcisi soyledir p ℏi iℏ displaystyle mathbf p hbar over i nabla i hbar nabla burada islemcisi ħ indirgenmis Planck sabiti ve i sanal birimdir Bu momentum islemcisinin cokca kullanilan seklidir ancak degisik baska tabanlarda degisik bicimler alabilir Ornegin momentum tabaninda momentum islemcisi soyle temsil edilir pps p pps p displaystyle mathbf p psi p p psi p burada ps p dalga fonksiyonuna etkiyen islemci p dalga fonksiyonu kere p degeri sonucunu verir Bu ayni konum islemcisinin dalga fonksiyonuna etkidikten sonra konum degeri x carpi dalga fonksiyonunu vermesi gibidir Elektromagnetizmada momentum Elektrik ve magnetik alanlar duragan ya da zaman icinde degisip degismediklerine bakilmaksizin momentum tasirlar Bir metal kure silindirsel kapasitor veya miknatis bir cubugun uzerindeki elektrostatik magnetostatik alanin P basinci asagidaki gibidir Pstatic W ϵ0ϵE22 1m0mB22 displaystyle P static W left epsilon 0 epsilon frac mathbf E 2 2 frac 1 mu 0 mu frac mathbf B 2 2 right burada W displaystyle W E displaystyle mathbf E B displaystyle mathbf B Sirasiyla elektromagnetik enerji yogunlugu elektrik alani ve magnetik alandir elektromagnetik basinc P W displaystyle P W kapasitoru patlatacak kadar guclu olabilir O halde elektrik ve magnetik alanlar da momentum tasirlar Isik gorulur UV radyo elektromagnetik bir dalgadir ve boylece momentuma sahiptir Fotonun kutlesi olmamasina ragmen yine de momentum tasir Bu ozellik gunes yelkeni gibi uygulamalara zemin hazirlar Dielektrik ortamdaki isigin momentumunun hesaplanmasi tartismalidir Bkz 1 3 Ocak 2012 tarihinde Wayback Machine sitesinde Momentum elektrodinamik bir sistemde korunur alandaki momentumdan hareket eden bolumlerin mekanik momentumuna donusebilir Bir alanin momentumunun hesabi genellikle ve belli bir hacim uzerinden integre edilmis Poynting vektorunun zaman icindeki degisimleri dikkate alinarak yapilir Bu ise bilesenleri enerji yogunlugu ve momentum yogunlugu olan bir tensor alanidir Elektromagnetik etkilesmeler soz konusu oldugunda kanonik momentuma karsilik gelen kuantum mekaniksel momentum islemcisi p mv displaystyle mathbf p m mathbf v Yerine P mv qA displaystyle mathbf P m mathbf v q mathbf A ile ifade edilir Burada A displaystyle mathbf A elektromagnetik vektor potansiyeli m displaystyle m yuklu parcacigin kutlesi v displaystyle mathbf v hizi q displaystyle q yukudur Acisal momentumAcisal momentum cember seklinde bir duzlemde donen bir cismin sahip oldugu bir ozelliktir Momentum gibi sabittir L r p displaystyle vec L vec r times vec p r Parcacigin secilen orijin noktasina gore uzaklik vektoru p Parcacigin momentumuKaynakca David 1960 2007 Fundamentals of Physics John Wiley amp Sons Chapter 9 Serway Raymond Jewett John 2003 Physics for Scientists and Engineers 6 ed Brooks Cole ISBN 0 534 40842 7 Stenger Victor J 2000 Timeless Reality Symmetry Simplicity and Multiple Universes Prometheus Books Chpt 12 in particular Tipler Paul 1998 Physics for Scientists and Engineers Vol 1 Mechanics Oscillations and Waves Thermodynamics 4th ed W H Freeman ISBN 1 57259 492 6 Hand Louis N Finch Janet D 1998 Analytical Mechanics Cambridge University Press Chapter 4 Dorn Bader Physik Gymnasium Gesamtband Sek 2 2000 Scroedel Verlag ISBN 3 507 10724 4 Metzler Physik J Grehn J Kause 4 Basim ISBN 978 3 507 10710 6Notlar TDK Bilim ve Sanat Terimleri Ana Sozlugu Erisim tarihi 18 Nisan 2011 olu kirik baglanti 30 Mart 2016 tarihinde kaynagindan arsivlendi Erisim tarihi 16 Nisan 2011 McGill amp King 1995 Engineering Mechanics An Introduction to Dynamics 3 bas PWS Publishing Company ISBN 0 534 93399 8 Hand Louis N Finch Janet D 1998 Analytical Mechanics Cambridge University Press Chapter 4 Pike Edward Roy Sabatier Pierre Celestin 2002 Scattering Academic Press s 703 ISBN 0 126 13760 9 Chpater 2 1 3 page 703
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State