Oran

Kesir, bir birimin bölündüğü parçalardan birinin veya birkaçının bütüne oranını ifade eden sayı. Kesir kavramı, ondalık sayılardan ve yüzdelerden ayırmak amacıyla sıklıkla sadece "bayağı kesirleri" tanımlamak için kullanılır.

1 çeyreği (1/4'ü) alınmış bir yaş pasta. Çizimde geriye kalan 3 çeyrek parça (3/4) gösteriliyor.

Bayağı kesirler

Örnekler
${\displaystyle {\tfrac {32}{45}}}$ 2 1/4 ^34 ½

İlk kesirler tam sayıların çarpmaya göre tersleriydi: iki parçanın biri, üç parçanın biri, dört parçanın biri şeklinde devam eden tarihi simgeler. Matematik ilerledikçe kesirlerin daha ileri bir türü olan ortaya çıktı.

Bu kesir türü bir pay ve paydadan oluşmaktadır: 1/2, 7/8 gibi. Pay birbirine eşit parça sayısını, payda ise bu parçalardan kaç tanesinin bütünü oluşturduğunu belirtir. Örneğin payın 3 paydanın ise 4 olduğu 3/4 kesrinde 3 rakamı kaç eşit parça olduğunu 4 ise bu parçalardan bütüne oluşturmak için kaç tane gerektiğini söyler.

Genellikle bir bölü çizgisi pay ve paydayı birbirinden ayırır. Çizgi 3/4 örneğindeki gibi yamuk ise eğik çizgi olarak adlandırılır. Eğer çizgi yatay ise kesir çizgisi olarak adlandırılır: 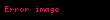${\displaystyle {\tfrac {3}{4}}}$

Bazen çizgi kullanılmayabilir: ³₄

Bilgisayar görüntü ve tipografisinde bayağı kesirler tek bir karakter olarak gösterilir: ½

Kesir Türleri

Basit kesirler

Bir kesir bir rasyonel sayının bir tam sayı (pay)'nın sıfır olmayan başka bir tam sayıya (payda) bölünmesi şeklinde yazılan sayılardır 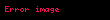${\displaystyle {\tfrac {1}{6}}}$.

Bayağı bir kesir payın mutlak değeri paydanınkinden küçük olduğu durumda basit kesir olarak adlandırılır bu durum birim kesrin mutlak değeri 1 den küçük ise geçerlidir.

Bileşik kesirler

Payı paydasına eşit veya payı paydasından büyük olan kesirler bileşik kesir olarak adlandırılır. Mesela ${\displaystyle {\tfrac {10}{3}}}$.

Tam sayılı kesirler

Tam sayılı bir kesir Bir tam sayı ile bir basit kesrin toplanması ile oluşur. Bu toplama herhangi bir toplama operatörü (+) olmadan gerçekleştirilir, Örneğin 2 tam ve 3 çeyrek keki belirtmek için, sayının kesirsel parçası ile tam sayı parçası yan yana yazılır: ${\displaystyle 2+{\tfrac {3}{4}}=2{\tfrac {3}{4}}}$.

Bu yazış şekli matematiksel düşünülerek iki sayıyı araya bir çarpma operatörü koymadan yapılmasıyla karıştırılmamalı.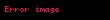${\displaystyle a{\tfrac {b}{c}}={\tfrac {a\cdot b}{c}}}$. Bu iki öğenin yan yana olmasıyla ilgili "anlam değişimi" aritmetik seviyesinin ötesindeki matematiksel konularda bileşik kesir tercih edilmesinin en azından kısmi bir sebebi.

Bir bileşik kesir, tam sayılı kesirleri yazmanın başka bir yolu olarak düşünülebilir. Tam sayılı bir kesir bileşik bir kesre 3 adımda dönüştürülebilir.

1. Tam sayı kısmını kesir kısmının paydasıyla çarp.
2. Çıkan sayıya payı ekle.
3. Çıkan toplama işleminin sonucu yeni (bileşik) kesrin payı olacak 'yeni' payda ise eski tam sayılı kesrin kesir bölümünün paydası olacaktır.

Benzer olarak bileşik bir kesir tam sayılı bir kesre dönüştürülebilir.

1. Payı paydaya böl.
2. Bölüm (kalan dışında) yeni tam sayı parçası kalan ise yeni tam sayılı kesrin kesir parçasının payı olacak.
3. Yeni payda bileşik kesrin paydasıyla aynı olacak.

Ondalık sayılar

Örnekler
0,7578 1,5 22,01

Kesirlerin daha da gelişmiş bir hali olan paydası virgül'den sonraki rakamların sayısı tarafından belirlenen 10 ve 10'un kuvvetleri olan kesirlerdir. Örneğin 0,75 ondalık sayısında pay 75 payda ise virgülden sonra 2 rakam olduğuna göre 10 un 2. kuvveti olan 100 dür.

Bayağı bir kesri ondalık hale getirmek için payı paydaya bölmek ve istenilen hassaslığa kadar yuvarlamak gerekir. Tersi şekilde bir ondalık sayı da bir bayağı kesre çevrilebilir. Örneğin 0,2230 ${\displaystyle {\tfrac {2230}{10000}}}$ olarak gösterilebilir. Eğer mümkünse kesir sadeleştirilir. Örneğin 0,25 ondalık sayısı 25/100 kesrine dönüştürüldükten sonra 1/4 olarak sadeleştirilir. Bu iki kesrin rakamsal değeri eşittir.

Dört işlem

Toplama ve çıkarma

Ondalık kesirler toplanırken veya çıkarılırken, virgüller alt alta gelecek şekilde yazılır ve doğal sayılardaki toplama-çıkarma işleminde olduğu gibi işlem yapılır. Sonuç, virgüllerin hizasından virgülle ayrılır.

 12,45 + 3,572 16,022 

Bölme

Bölen virgülden kurtulacak biçimde 10'un kuvveti ile çarpılır (virgül ondalık ifadenin sonuna kadar sağa kaydırılır). Bölünen de 10'un aynı kuvveti ile çarpılır (virgül "bölendeki kadar" sağa kaydırılır). Daha sonra virgül yokmuş gibi işlem yapılır.

0,3046 / 0,02 = ? bölünen/ bölen 

0,3046 x 10 x 10 = 30,46 0,02 x 10 x 10 = 2 30,46 / 2 = 15,23 (virgül hem bölünende hem de bölende 2 hâne sağa kaydırıldı) 

Çarpma

• Ondalık sayılar çarpılırken her iki çarpandaki tam sayılar virgül yokmuş gibi çarpılır.
• Daha sonra çarpanlardaki (her ikisindeki) virgülden sonraki rakam "adedi" toplanır.
• Çarpımın sonundan başlanarak sola doğru bu rakam adedi kadar virgül kaydırılır. Örnek:

0,015 x 0,26 = ?

15 x 26 = 390

015'teki 3 rakam + 26'daki 2 rakam = 5 rakam

0₅0₄0₃3₂9₁0

0,015 x 0,26 = 0,0039 (sondaki 0 bir anlam ifade etmediği için düşer)

Kesirlerle işlemler

Toplama ve Çıkarma

Toplama ve çıkarma işlemi yapılırken paydalar aynı ise işlem şöyle yapılır

Örnek:${\displaystyle 7 \over 13}$${\displaystyle +}$${\displaystyle 8 \over 13}$${\displaystyle =}$${\displaystyle 15 \over 13}$ veya ${\displaystyle 8 \over 10}$${\displaystyle -}$${\displaystyle 3 \over 10}$${\displaystyle =}$${\displaystyle 5 \over 10}$

Paylar farklı ama paydalar aynı olunca paylar toplanır veya çıkartılır, payda ise olduğu gibi kalır.

Eğer paydalar da farklıysa şöyle yapılır;

Örnek:${\displaystyle 6 \over 8}$${\displaystyle +}$${\displaystyle 4 \over 6}$${\displaystyle =}$${\displaystyle 6\times 6 \over 8\times 6}$${\displaystyle +}$${\displaystyle 4\times 8 \over 6\times 8}$ veya ${\displaystyle 6 \over 8}$${\displaystyle -}$${\displaystyle 4 \over 6}$${\displaystyle =}$${\displaystyle 6\times 6 \over 8\times 6}$${\displaystyle -}$${\displaystyle 4\times 8 \over 6\times 8}$

Çarpma

Çarpma işlemi yapılırken pay ile paydalar doğrudan çarpılır.

NOT:Aynı kural bölme işlemi için de geçerlidir.

Örnek:${\displaystyle 7 \over 9}$${\displaystyle \times }$${\displaystyle 9 \over 6}$${\displaystyle =}$${\displaystyle 63 \over 54}$

Bölme

Bölme işleminin kısaca iki kuralı vardır

1.Kural Pay ile paydalar doğrudan bölünür

Örnek:${\displaystyle 9 \over 15}$${\displaystyle \div }$${\displaystyle 3 \over 3}$${\displaystyle =}$${\displaystyle 3 \over 5}$

2.Kural İlk kesir olduğu gibi kalır, diğer kesirlerin pay ile paydalarının yerleri değişir ve aradaki bölme işlemi çarpma işlemine dönüştürülür ve çarpma işlemi kuralına göre uygulanır

${\displaystyle 7 \over 9}$${\displaystyle \div }$${\displaystyle 6 \over 16}$${\displaystyle =}$${\displaystyle 7 \over 9}$${\displaystyle \times }$${\displaystyle 16 \over 6}$${\displaystyle =}$${\displaystyle 96 \over 54}$

Yüzdeler

Örnekler
%73 %100 %0,1

Kesirlerin 3. bir türü olan yüzdelerde payda her zaman 100'dür bu yüzden %75 ifadesi 75/100 anlamına gelir.

Kesirlerin diğer işlevleri ise oranları göstermek ve bölme işlemini belirtmektir. Bu nedenle 3/4 kesri 3'ün 4'e oranını aynı zamanda 3÷4 bölme işlemini gösterir.

Matematikte kesir olarak gösterilebilecek bütün sayıların kümesi m/n, m ve n nin birer tam sayı ve n nin 0 olmadığı bu durumda oluşan küme Rasyonel Sayılar olarak adlandırılır. Bu küme Q ile gösterilir.

Kesir terimi sürekli kesir ve cebirsel kesir terimlerinin içindede geçmektedir. --Bakınız özel durumlar.

Ayrıca bakınız

• Altın oran

(Sayı sistemleri) Karmaşık ${\displaystyle :\;\mathbb {C} }$ Reel ${\displaystyle :\;\mathbb {R} }$ Rasyonel ${\displaystyle :\;\mathbb {Q} }$ Tam sayı ${\displaystyle :\;\mathbb {Z} }$ Doğal ${\displaystyle :\;\mathbb {N} }$ Sıfır: 0 Bir: 1 Asal sayılar Bileşik sayılar Negatif tam sayılar Kesir Devirli ondalık sayı İrrasyonel Cebirsel irrasyonel Aşkın Sanal