Rasyonel sayılar, iki tam sayı arasındaki oranı temsil eden, bir pay p ve sıfırdan farklı bir payda q olmak üzere, bir bölme işlemi veya kesir formunda ifade edilebilen sayıları tanımlar. Örneğin, rasyonel bir sayı olarak kabul edilir, bu kapsamda her tam sayı da (mesela, gibi) rasyonel sayılar kategorisindedir. Rasyonel sayılar kümesi, çoğunlukla kalın harf biçimindeki Q veya kullanılarak şeklinde ifade edilir.


Rasyonel sayı, reel sayılar kümesine ait bir sayıdır. Bu sayılar, ondalık açılımlarının sonlu sayıda rakam içermesiyle karakterize edilir ve bu açılım ya bir noktadan sonra sonlanır (örneğin: 3/4 = 0.75) ya da belirli bir dizinin rakamlarının sürekli olarak tekrar edilmesiyle devam eder (örneğin: 9/44 = 0.20454545...). Bu özellik, yalnızca on tabanlı sistemde geçerli olmayıp, ikili, on altılı gibi diğer tüm tam sayı taban sistemlerinde de geçerlidir.
Rasyonel olmayan bir reel sayı, irrasyonel olarak tanımlanır. Bu kapsamda irrasyonel sayılara örnek olarak Karekök 2 (), π, e ve altın oran (φ) gösterilebilir. Rasyonel sayılar kümesinin sayılabilir bir yapıda olması ve reel sayılar kümesinin ise bir yapıya sahip olması sebebiyle, reel sayıların büyük bir çoğunluğu irrasyoneldir.
Rasyonel sayılar, belirli tam sayı çiftleri olan (p, q) için, q ≠ 0 koşulu altında, olarak formel bir şekilde ifade edilebilir. Bu çerçevede, eşdeğerlik ilişkisi şu şekilde tanımlanır:
Bu bağlamda, kesri, belirtilen (p, q) çiftinin eşdeğerlik sınıfını temsil eder.
Rasyonel sayılar tam sayıların bir genişlemesidir. kümesi genelde şöyle tanımlanır:
(a ve b tam sayı ve b sıfır olmamak üzere a/b şeklindeki sayılara rasyonel sayı denir)
ve veya eşdeğer rasyonel sayılardır. Dolayısıyla her rasyonel sayı sonsuz şekilde ifade edilebilir. Rasyonel sayıların en basit biçimi ve tam sayılarının ortak bölen'inin olmadığı ifadesidir.
Her tam sayı rasyonel sayıdır. Çünkü veya veya şeklinde yani rasyonel sayı tanımına uygun biçimde yazılabilirler. Rasyonel sayılar kümesi , tam sayılar kümesi 'yi kapsar. Yani .
Daha ince bir tanımı ise tam sayılar üzerinden tanımlanacak bir denklik bağıntısıyla yapılabilir. Böylece her denklik sınıfı bir rasyonel sayı olarak anılır. kümesinden seçilmiş keyfi (a,b) ve (c,d) ögeleri için "~" bağıntısı olarak tanımlansın. Bunun bir denklik bağıntısı olduğu kolaylıkla kanıtlanabilir. Bu durumda, denklik sınıfları olurlar. Rasyonel sayı ise basitçe şeklinde tanımlanır. Tanımda paydanın sıfır olmama şartı ifadesinin tanımlanmamış olmasındandır. Bir sayının sıfıra bölümü tanımsızdır.
Sıfırdan büyük olan rasyonel sayılara pozitif rasyonel sayılar, sıfırdan küçük rasyonel sayılar da negatif rasyonel sayılar denir. Pozitif rasyonel sayılar kümesi ile, negatif rasyonel sayılar kümesi ile gösterilir.

Yandaki şekilde, bir yuvarlak pasta 4 eş parçaya bölünmüş ve bu 4 eş parçalardan her birisi olarak görülmektedir. Ancak bir parça alınmış olduğundan kalan eksikdir. Geriye kalan, dört eşit parçaya bölünmüş bütünün üç tane parçası (yani 3'te 4 oranı) veya (kesiri)dir. Bu ifadesi şeklinde gösterilir. Burada ifadede kesir çizgisinin üstündeki değere (yani 3'e) pay, kesir çizgisinin altındaki değere (yani 4’e) payda denir. Bu kesir, “üç bölü dört” ya da “dörtte üç” diye okunur.
Rasyonel sayılar, toplama ve çarpma işlemleri ile birleştirildiğinde, tam sayıları barındıran ve aynı zamanda tam sayılar içeren herhangi bir matematiksel cismin (İng. field) bir parçası olan bir cismi meydana getirir. Bu bağlamda, rasyonel sayılar cismi bir asal cisim niteliğindedir ve bir cismin sıfır karakteristiğe sahip olması, yalnızca o cismin rasyonel sayıları bir alt cisim olarak barındırması ile mümkündür. 'nun sonlu genişlemeleri cebirsel sayı cisimleri olarak isimlendirilir ve 'nun cebirsel kapanışı, cebirsel sayılar cismidir.
Matematiksel analiz çerçevesinde, rasyonel sayılar, reel sayılar içerisinde yoğun bir alt küme teşkil eder. Reel sayıların tanımlanması, rasyonel sayılar baz alınarak, Cauchy dizileri, veya sonsuz ondalık sayılar kullanılarak gerçekleştirilebilir.
Terminoloji
"Rasyonel" terimi, 
Etimoloji
Günümüzdeki "rasyonel sayılar", "rasyo" ("oran") kavramları ile ilişkilendirilse de, "rasyonel" sözcüğü, "rasyo" teriminin bir türevi olmayıp, tam tersine, "rasyo" sözcüğü "rasyonel"den kaynaklanmaktadır. "Rasyo" (İng. ratio) teriminin çağdaş anlamda ilk kez kullanıldığı dönem İngilizcede yaklaşık olarak 1660 yılına dayanırken, "rasyonel" ifadesinin sayıları tanımlama amacıyla kullanımı bu tarihten yaklaşık bir yüzyıl önce, 1570 yılında meydana gelmiştir. "Rasyonel" teriminin bu özel anlamı, "irrasyonel" teriminin matematiksel bağlamda ilk kullanımından, yani 1551 yılından türemiş olup, Öklit'in eserlerinin çevirilerinde özgün kullanımını izleyerek (Grekçe: ἄλογος) kullanılmıştır.
Bu alışılmadık tarihi olgular zinciri, antik Yunan matematikçilerinin, kendilerini irrasyonel olarak nitelendirilen uzunlukları sayı olarak kabul etmekten çekinerek, böylece sapkınlıktan uzak durmayı tercih etmelerinden kaynaklanmaktadır. Dolayısıyla, bu tür uzunluklar, konuşulmaması gereken, yani Yunancada (Grekçe: ἄλογος) ifade edilen mantıksız anlamına gelen irrasyonel kelimesi ile tanımlanmıştır.
Aritmetik

İndirgenemez kesir
Her bir rasyonel sayı, 
Bir rasyonel sayının 
Tam sayı ifadelendirme
Her bir tam sayı n, rasyonel bir sayı biçiminde 
Eşitlik ilkesi
ifadesi, ancak ve ancak
olduğunda doğrudur.
Her iki kesir de kanonik forma sahip olduğunda:
, ancak ve ancak
ve
eşitlikleri sağlandığında geçerli olur.
İki rasyonel sayının eşitliği, o sayıların pay ve paydalarının rasyonel olmasıyla anlaşılır. 

Bu koşul, yukarıdaki tanımdan çıkartılabilir. İki rasyonel sayı aynı denklik sınıfındaysa birbirine eşittir, Denklik bağıntısı da zaten 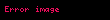
Sıralama
Eğer her iki paydanın da pozitif olduğu durumlar (özellikle her iki kesirin kanonik formda olduğu durumlar) göz önüne alınırsa:
ancak ve ancak
şeklinde olur.
Diğer yandan, paydalardan biri negatifse, negatif paydaya sahip her kesirin önce pozitif bir paydaya sahip eşdeğer bir forma dönüştürülmesi gerekir—bunun için hem payının hem de paydasının işaretinin değiştirilmesi gerekir.
Paydaları eşit olan rasyonel sayılar
- Paydaları eşit olan rasyonel oranlar için payı büyük olan daha büyük, payı küçük olan daha küçüktür.
- Örneğin
- Burada paydalar eşit ve yirmidir. Pay değerleri karşılaştırılınca soldaki pay 7 sağdaki pay 3'ten daha büyük olduğu için, soldaki rasyonel oran daha büyüktür.
- Unutmamalıdır ki negatif paylar karşılaştırılırken sadece mutlak değerlerin karşılaştırılması hatalı olup negatif işaretlerinin de ele alınması ve :negatif sayılı pay değerlerde mutlak değeri büyük görünen sayının daha küçük olduğu hatırlanmalıdır:
- Payda 20'ye eşit olup sağdaki negatif pay değeri -3, soldaki negatif pay değeri olan -7'den daha büyük olduğu için sağdaki oran daha büyüktür.
Payları eşit olan rasyonel sayılar
- Payı eşit olan rasyonel sayılar için ise paydaları eşit olanın tam tersi bir kural uygulanır:
- Paylar eşit olduğunda bölünen parça sayısı yani payda büyüdükçe oluşan parça boyutları daha küçük olacaktır.
Payları ya da paydaları eşit olmayan rasyonel sayılar
- Bu şekildeki durumlarda karşılaştırmadan evvel paydaların eşitlenmesi veya içler dışlar çarpımı yapılmasını gerektirir.
- Paydaların eşitlenmesi
- Her iki rasyonel sayının da birbirlerinin paydalarıyla genişletilmesini gerektirir.
- Paydaların eşitlenmesi
- Yukarıda görüldüğü gibi genişletme işleminden sonra oluşan paydaların ikisi de
yani 40'tır. Yukarıda görüldüğü gibi karşılaştırılabilir.
- Yukarıda görüldüğü gibi genişletme işleminden sonra oluşan paydaların ikisi de
- İçler dışlar çarpımı
- Birinci rasyonel sayının payının ikincinin paydasına, ikincinin paydasının ise birincinin payıyla çarpılmasıdır:
- İçler dışlar çarpımı
.
Toplama
İki kesrin toplanması şu şekilde gerçekleştirilir: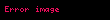
Eğer her iki kesir de kanonik formdaysa, sonuç ancak ve ancak b, d aralarında asal tam sayılar olması durumunda kanonik formda olacaktır.
Çıkarma
Eğer her iki kesir de kanonik formdaysa, sonuç ancak ve ancak b, d aralarında asal tam sayılar ise kanonik formdadır.
Çarpma
Çarpma kuralı şu şekildedir:
burada sonuç, her iki orijinal kesir de kanonik formda olsa bile, bir olabilir.
Tersi
Herhangi bir rasyonel sayı 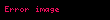
.
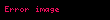
Sıfırdan farklı bir rasyonel sayı 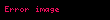
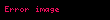

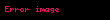
Bölme
Eğer b, c, d sıfırdan farklıysa, bölme kuralı şu şekildedir:
Böylece, 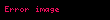

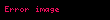
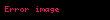
Tam sayı kuvvetine üs alma
n negatif olmayan bir tam sayı olduğunda,
Sonuç, 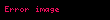
Eğer a ≠ 0, o zaman
Eğer 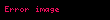


Sürekli kesir gösterimi
Bir sonlu sürekli kesir ifadesi, aşağıdaki formda gösterilebilir:
bu ifadede, an tam sayıları temsil eder. Herhangi bir rasyonel sayı 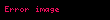
Diğer gösterimler
- Bayağı kesir:
- Karmaşık sayı:
- Bir kullanılarak devirli sayı ile:
- Parantez kullanılarak devirli sayı ile:
- Geleneksel tipografi kullanılarak :
- kısaltılmış notasyon ile sürekli kesir:
- :
- (Asal üs ayrışımı):
- :
aynı rasyonel değeri temsil etmenin farklı yollarıdır.
Tanım

Rasyonel sayılar, tam sayıların sıralı çiftlerine dayanan denklik sınıfları biçiminde kurulabilir.
Daha kesin bir ifadeyle, 
ile tanımlanmıştır.
Toplama ve çarpma işlemleri aşağıdaki kurallarla tanımlanabilir:
Bu denklik ilişkisi, daha önce tanımlanmış toplama ve çarpma işlemleriyle uyumlu bir olarak işlev görür; böylece rasyonel sayılar kümesi 

Bir (m, n) çiftinin denklik sınıfı, 
ise aynı denklik sınıfına dahildir (yani eşdeğerdirler). Bu durum,
ancak ve ancak
olduğunda mümkündür.
Her denklik sınıfı 
Her denklık sınıfı, benzersiz bir kanonik temsilci elemanı içerir. Kanonik temsilci, denklik sınıfındaki (m, n) benzersiz çiftidir öyle ki m ve n aralarında asaldır ve n > 0. Bu, rasyonel sayının olarak adlandırılır.
Tam sayılar, tam sayı n'yi rasyonel sayı 
Rasyonel sayılar üzerinde, tam sayıların doğal sıralamasını genişleten bir tanımlanabilir. Buna göre
Eğer
Özellikler
Yukarıda gösterilen toplama ve çarpma işlemleriyle birlikte, tüm rasyonel sayıların kümesi 



Yukarıda tanımlanan sırayla, 




Rasyonel sayılar, bir kümedir: herhangi iki rasyonel sayı arasında başka bir rasyonel sayı bulunur ve dolayısıyla sonsuz sayıda başka rasyonel sayı bulunur. Örneğin,
(
En küçük veya en büyük elemanı olmayan, sayılabilir, yoğun (yukarıdaki anlamda) ve tamamen sıralı bir küme, rasyonel sayılarla .
Sayılabilirlik

Tüm rasyonel sayılar kümesinin sayılabilir olduğu, sağ tarafta yer alan gösterim ile açıklanmıştır. Her bir rasyonel sayının, iki tam sayının oranı şeklinde ifade edilebilme özelliği göz önünde bulundurulduğunda, üzerindeki her bir noktaya, bir Kartezyen koordinat sistemi benzeri bir yaklaşımla, iki tam sayı atanması mümkündür; böylelikle her bir kafes noktası bir rasyonel sayı ile ilişkilendirilebilir. Bu yöntem, sağlanan grafikte kırmızı ile işaretlenmiş olan, birçok farklı kafes noktasının aynı rasyonel sayıyı temsil etmesi gibi bir fazlalığın ortaya çıkmasına neden olmaktadır. Bu fazlalığın bir örneği, sağ alt köşeye doğru diagonal bir hat üzerinde gözlemlenebilir; bu tür oranlar, herhangi bir sayının kendisi ile bölünmesi durumunda daima bir değerini alacaktır.
Bu tür fazlalıklar olmadan tüm rasyonel sayıların tanımı mümkündür: örnekler arasında ve bulunmaktadır.
Tüm rasyonel sayılar kümesi sayılabilir olduğu ve tüm reel sayılar kümesi (aynı zamanda tüm irrasyonel sayılar kümesi) sayılamaz olduğu için, rasyonel sayılar kümesi bir , yani anlamında neredeyse tüm reel sayılar irrasyoneldir.
Reel sayılar ve topolojik özellikler
Rasyonel sayılar, reel sayıların yoğun bir alt kümesidir; her reel sayının yanında keyfi olarak yakın rasyonel sayılar vardır. İlgili bir özellik, rasyonel sayıların, olarak genişlemelere sahip tek sayılar olmasıdır.
Reel sayıların alışılageldik topolojisi içinde, rasyonel sayılar ne bir açık küme ne de bir .
Sıralarının bir sonucu olarak, rasyonel sayılar bir taşır. Rasyonel sayılar, reel sayıların bir alt uzayı olarak, ayrıca bir altuzay topolojisi taşır. Rasyonel sayılar, metriği 



p-sel sayılar
Yukarıda bahsedilen mutlak değer metriğine ek olarak, 
p bir asal sayı olsun ve sıfırdan farklı herhangi bir tam sayı a için, 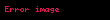
Ayrıca 

olarak belirleyelim.
O zaman

Metrik uzay 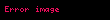


Ayrıca bakınız
|
Not listesi
Kaynakça
- ^ Rosen, Kenneth (2007). Discrete Mathematics and its Applications (6 bas.). New York, NY: McGraw-Hill. ss. 105, 158-160. ISBN .
- ^ "Rational number". Encyclopedia Britannica (İngilizce). 11 Aralık 2021 tarihinde kaynağından . Erişim tarihi: 11 Ağustos 2020.
- ^ Weisstein, Eric W. "Rational Number". Wolfram MathWorld (İngilizce). 14 Temmuz 2023 tarihinde kaynağından . Erişim tarihi: 11 Ağustos 2020.
- ^ Rosen, Kenneth (2007). Discrete Mathematics and its Applications (6 bas.). New York, NY: McGraw-Hill. ss. 105, 158-160. ISBN .
- ^ a b c d e f g h i j k l Biggs, Norman L. (2002). Discrete Mathematics. India: Oxford University Press. ss. 75-78. ISBN .
- ^ Robinson, Julia (1996). The Collected Works of Julia Robinson (İngilizce). American Mathematical Soc. ISBN .
- ^ Lass, Harry (18 Kasım 2009). Elements of Pure and Applied Mathematics (İngilizce). Courier Corporation. ISBN .
- ^ Gilbert, Jimmie; (2005). Elements of Modern Algebra (6.6yayıncı=Thomson Brooks/Cole bas.). Belmont, CA. ss. 243-244. ISBN .
- ^ a b Oxford English Dictionary (2.2tarih=1989 bas.). Oxford University Press.
- ^ (9 Mayıs 2017). "Does rational come from ratio or ratio come from rational". Stack Exchange (İngilizce). 17 Nisan 2021 tarihinde kaynağından . Erişim tarihi: 19 Mart 2021.
- ^ Coolman, Robert (29 Ocak 2016). "How a Mathematical Superstition Stultified Algebra for Over a Thousand Years" (İngilizce). 21 Aralık 2021 tarihinde kaynağından . Erişim tarihi: 20 Mart 2021.
- ^ Kramer, Edna (1983). The Nature and Growth of Modern Mathematics. Princeton University Press. s. 28.
- ^ a b c d e f g h "Fraction - Encyclopedia of Mathematics". encyclopediaofmath.org. 27 Eylül 2021 tarihinde kaynağından . Erişim tarihi: 17 Ağustos 2021.
- ^ Sūgakkai, Nihon (1993). Encyclopedic Dictionary of Mathematics, Volume 1. London, England: MIT Press. s. 578. ISBN .
- ^ Giese, Martin; Schönegge, Arno (December 1995). Any two countable densely ordered sets without endpoints are isomorphic - a formal proof with KIV (PDF). 25 Kasım 2021 tarihinde kaynağından (PDF). Erişim tarihi: 17 Ağustos 2021.
- ^ Anthony Vazzana; David Garth (2015). Introduction to Number Theory (2nd, revised bas.). CRC Press. s. 1. ISBN . Extract of page 1
- ^ Weisstein, Eric W. "p-adic Number". Wolfram MathWorld (İngilizce). 2 Mayıs 2021 tarihinde kaynağından . Erişim tarihi: 17 Ağustos 2021.
Dış bağlantılar
| Wikimedia Commons'ta Rasyonel sayılar ile ilgili ortam dosyaları bulunmaktadır. |

- Hazewinkel, Michiel, (Ed.) (2001), "Rational number", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN
- "Rational Number" From MathWorld – A Wolfram Web Resource
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Rasyonel sayilar iki tam sayi arasindaki orani temsil eden bir pay p ve sifirdan farkli bir payda q olmak uzere bir bolme islemi veya kesir formunda ifade edilebilen sayilari tanimlar Ornegin 37 displaystyle tfrac 3 7 rasyonel bir sayi olarak kabul edilir bu kapsamda her tam sayi da mesela 5 51 displaystyle 5 tfrac 5 1 gibi rasyonel sayilar kategorisindedir Rasyonel sayilar kumesi cogunlukla kalin harf bicimindeki Q veya kullanilarak Q displaystyle mathbb Q seklinde ifade edilir Rasyonel sayilar kumesini temsil eden simgeRasyonel sayilar kumesi Q displaystyle mathbb Q reel sayilar kumesi R displaystyle mathbb R icerisinde konumlanmaktadir ki bu reel sayilar kumesi de karmasik sayilar kumesi C displaystyle mathbb C tarafindan kapsanmaktadir Rasyonel sayilar kumesi ayni zamanda tam sayilar kumesi Z displaystyle mathbb Z icermekte olup bu tam sayilar kumesi de dogal sayilar kumesi N displaystyle mathbb N tarafindan kapsanmaktadir Rasyonel sayi reel sayilar kumesine ait bir sayidir Bu sayilar ondalik acilimlarinin sonlu sayida rakam icermesiyle karakterize edilir ve bu acilim ya bir noktadan sonra sonlanir ornegin 3 4 0 75 ya da belirli bir dizinin rakamlarinin surekli olarak tekrar edilmesiyle devam eder ornegin 9 44 0 20454545 Bu ozellik yalnizca on tabanli sistemde gecerli olmayip ikili on altili gibi diger tum tam sayi taban sistemlerinde de gecerlidir Rasyonel olmayan bir reel sayi irrasyonel olarak tanimlanir Bu kapsamda irrasyonel sayilara ornek olarak Karekok 2 2 displaystyle sqrt 2 p e ve altin oran f gosterilebilir Rasyonel sayilar kumesinin sayilabilir bir yapida olmasi ve reel sayilar kumesinin ise bir yapiya sahip olmasi sebebiyle reel sayilarin buyuk bir cogunlugu irrasyoneldir Rasyonel sayilar belirli tam sayi ciftleri olan p q icin q 0 kosulu altinda olarak formel bir sekilde ifade edilebilir Bu cercevede esdegerlik iliskisi su sekilde tanimlanir p1 q1 p2 q2 p1q2 p2q1 displaystyle p 1 q 1 sim p 2 q 2 iff p 1 q 2 p 2 q 1 Bu baglamda pq displaystyle tfrac p q kesri belirtilen p q ciftinin esdegerlik sinifini temsil eder Rasyonel sayilar tam sayilarin bir genislemesidir Q displaystyle mathbb Q kumesi genelde soyle tanimlanir Q ab a b Z b 0 displaystyle mathbb Q frac a b a b in mathbb Z land b neq 0 a ve b tam sayi ve b sifir olmamak uzere a b seklindeki sayilara rasyonel sayi denir 23 displaystyle frac 2 3 ve 46 displaystyle frac 4 6 veya 69 displaystyle frac 6 9 esdeger rasyonel sayilardir Dolayisiyla her rasyonel sayi sonsuz sekilde ifade edilebilir Rasyonel sayilarin en basit bicimi a displaystyle a ve b displaystyle b tam sayilarinin ortak bolen inin olmadigi a b displaystyle a b ifadesidir Her tam sayi rasyonel sayidir Cunku 3 31 displaystyle 3 frac 3 1 veya 0 01 displaystyle 0 frac 0 1 veya 43 431 displaystyle 43 frac 43 1 seklinde yani rasyonel sayi tanimina uygun bicimde yazilabilirler Rasyonel sayilar kumesi Q displaystyle mathbb Q tam sayilar kumesi Z displaystyle mathbb Z yi kapsar Yani Z Q displaystyle mathbb Z subset mathbb Q Daha ince bir tanimi ise tam sayilar uzerinden tanimlanacak bir denklik bagintisiyla yapilabilir Boylece her denklik sinifi bir rasyonel sayi olarak anilir Z Z displaystyle mathbb Z times mathbb Z kumesinden secilmis keyfi a b ve c d ogeleri icin bagintisi a b c d ad bc b d 0 displaystyle a b sim c d Leftrightarrow ad bc quad b d not 0 olarak tanimlansin Bunun bir denklik bagintisi oldugu kolaylikla kanitlanabilir Bu durumda denklik siniflari a b a b a b c d displaystyle overline a b a b a b sim c d olurlar Rasyonel sayi ise basitce ab a b displaystyle frac a b overline a b seklinde tanimlanir Tanimda paydanin sifir olmama sarti a0 displaystyle frac a 0 ifadesinin tanimlanmamis olmasindandir Bir sayinin sifira bolumu tanimsizdir Sifirdan buyuk olan rasyonel sayilara pozitif rasyonel sayilar sifirdan kucuk rasyonel sayilar da negatif rasyonel sayilar denir Pozitif rasyonel sayilar kumesi Q displaystyle mathbb Q ile negatif rasyonel sayilar kumesi Q displaystyle mathbb Q ile gosterilir Dorde bolunup dortte biri kesilip alinmis ve geri kalan dortte ucu gosterilen bir yuvarlak pasta Yandaki sekilde bir yuvarlak pasta 4 es parcaya bolunmus ve bu 4 es parcalardan her birisi 14 displaystyle frac 1 4 olarak gorulmektedir Ancak bir parca alinmis oldugundan kalan eksikdir Geriye kalan dort esit parcaya bolunmus butunun uc tane parcasi yani 3 te 4 orani veya kesiri dir Bu 34 displaystyle frac 3 4 ifadesi seklinde gosterilir Burada ifadede kesir cizgisinin ustundeki degere yani 3 e pay kesir cizgisinin altindaki degere yani 4 e payda denir Bu kesir uc bolu dort ya da dortte uc diye okunur Rasyonel sayilar toplama ve carpma islemleri ile birlestirildiginde tam sayilari barindiran ve ayni zamanda tam sayilar iceren herhangi bir matematiksel cismin Ing field bir parcasi olan bir cismi meydana getirir Bu baglamda rasyonel sayilar cismi bir asal cisim niteligindedir ve bir cismin sifir karakteristige sahip olmasi yalnizca o cismin rasyonel sayilari bir alt cisim olarak barindirmasi ile mumkundur Q displaystyle mathbb Q nun sonlu genislemeleri cebirsel sayi cisimleri olarak isimlendirilir ve Q displaystyle mathbb Q nun cebirsel kapanisi cebirsel sayilar cismidir Matematiksel analiz cercevesinde rasyonel sayilar reel sayilar icerisinde yogun bir alt kume teskil eder Reel sayilarin tanimlanmasi rasyonel sayilar baz alinarak Cauchy dizileri veya sonsuz ondalik sayilar kullanilarak gerceklestirilebilir Terminoloji Rasyonel terimi Q displaystyle mathbb Q kumesine yapilan atiflarda bir rasyonel sayinin iki tam sayinin oranini temsil etmesi gercegine isaret eder Matematik alaninda rasyonel siklikla rasyonel sayi teriminin kisaltmasi olarak kullanilmaktadir Rasyonel sifati zaman zaman katsayilarin rasyonel sayilar oldugunu ifade eder Mesela rasyonel koordinatlara sahip bir nokta olarak adlandirilir rasyonel sayilardan olusan bir matrise rasyonel matris denir rasyonel katsayilara sahip bir polinoma rasyonel polinom denilebilir ancak rasyoneller uzerinde bir polinom ifadesi rasyonel ifade ile rasyonel fonksiyon arasindaki muhtemel karisikliklari engellemek amaciyla genellikle tercih edilir Bununla birlikte rasyonel egri rasyoneller uzerinde tanimlanmis bir egri anlamina gelmez bunun yerine rasyonel fonksiyonlarla parametrize edilebilen bir egriyi ifade eder EtimolojiGunumuzdeki rasyonel sayilar rasyo oran kavramlari ile iliskilendirilse de rasyonel sozcugu rasyo teriminin bir turevi olmayip tam tersine rasyo sozcugu rasyonel den kaynaklanmaktadir Rasyo Ing ratio teriminin cagdas anlamda ilk kez kullanildigi donem Ingilizcede yaklasik olarak 1660 yilina dayanirken rasyonel ifadesinin sayilari tanimlama amaciyla kullanimi bu tarihten yaklasik bir yuzyil once 1570 yilinda meydana gelmistir Rasyonel teriminin bu ozel anlami irrasyonel teriminin matematiksel baglamda ilk kullanimindan yani 1551 yilindan turemis olup Oklit in eserlerinin cevirilerinde ozgun kullanimini izleyerek Grekce ἄlogos kullanilmistir Bu alisilmadik tarihi olgular zinciri antik Yunan matematikcilerinin kendilerini irrasyonel olarak nitelendirilen uzunluklari sayi olarak kabul etmekten cekinerek boylece sapkinliktan uzak durmayi tercih etmelerinden kaynaklanmaktadir Dolayisiyla bu tur uzunluklar konusulmamasi gereken yani Yunancada Grekce ἄlogos ifade edilen mantiksiz anlamina gelen irrasyonel kelimesi ile tanimlanmistir Aritmetika b c d Q displaystyle a b c d in mathbb Q olmak uzere Indirgenemez kesir Her bir rasyonel sayi ab displaystyle tfrac a b seklinde a ve b aralarinda asal tam sayilar olmak uzere ve b gt 0 kosuluyla olarak essiz bir bicimde gosterilebilir Bu durum genellikle rasyonel sayinin olarak isimlendirilir Bir rasyonel sayinin ab displaystyle tfrac a b baslangic noktasindan kanonik formuna ulasilmasi a ve b yi onlarin en buyuk ortak bolenine bolerek ve eger b lt 0 ise elde edilen pay ve paydanin isaretinin degistirilmesi islemiyle mumkun olmaktadir Tam sayi ifadelendirme Her bir tam sayi n rasyonel bir sayi biciminde n1 displaystyle tfrac n 1 olarak gosterilebilir ki bu rasyonel sayilar baglaminda onun kanonik formunu temsil eder Esitlik ilkesi ab cd displaystyle frac a b frac c d ifadesi ancak ve ancak ad bc displaystyle ad bc oldugunda dogrudur Her iki kesir de kanonik forma sahip oldugunda ab cd displaystyle frac a b frac c d ancak ve ancak a c displaystyle a c ve b d displaystyle b d esitlikleri saglandiginda gecerli olur Iki rasyonel sayinin esitligi o sayilarin pay ve paydalarinin rasyonel olmasiyla anlasilir a b c d Z displaystyle a b c d in mathbb Z olmak uzere ab displaystyle frac a b ve cd displaystyle frac c d iki rasyonel sayi ise bu iki sayi ancak ad bc displaystyle ad bc oldugunda esittir Bu kosul yukaridaki tanimdan cikartilabilir Iki rasyonel sayi ayni denklik sinifindaysa birbirine esittir Denklik bagintisi da zaten ad bc displaystyle ad bc kosulunu icermekteydi Siralama Eger her iki paydanin da pozitif oldugu durumlar ozellikle her iki kesirin kanonik formda oldugu durumlar goz onune alinirsa ab lt cd displaystyle frac a b lt frac c d ancak ve ancak ad lt bc displaystyle ad lt bc seklinde olur Diger yandan paydalardan biri negatifse negatif paydaya sahip her kesirin once pozitif bir paydaya sahip esdeger bir forma donusturulmesi gerekir bunun icin hem payinin hem de paydasinin isaretinin degistirilmesi gerekir Paydalari esit olan rasyonel sayilar Paydalari esit olan rasyonel oranlar icin payi buyuk olan daha buyuk payi kucuk olan daha kucuktur Ornegin dd 720 gt 320 displaystyle frac 7 20 gt frac 3 20 Burada paydalar esit ve yirmidir Pay degerleri karsilastirilinca soldaki pay 7 sagdaki pay 3 ten daha buyuk oldugu icin soldaki rasyonel oran daha buyuktur Unutmamalidir ki negatif paylar karsilastirilirken sadece mutlak degerlerin karsilastirilmasi hatali olup negatif isaretlerinin de ele alinmasi ve negatif sayili pay degerlerde mutlak degeri buyuk gorunen sayinin daha kucuk oldugu hatirlanmalidir Payda 20 ye esit olup sagdaki negatif pay degeri 3 soldaki negatif pay degeri olan 7 den daha buyuk oldugu icin sagdaki oran daha buyuktur Paylari esit olan rasyonel sayilar Payi esit olan rasyonel sayilar icin ise paydalari esit olanin tam tersi bir kural uygulanir 56 gt 510 displaystyle frac 5 6 gt frac 5 10 Paylar esit oldugunda bolunen parca sayisi yani payda buyudukce olusan parca boyutlari daha kucuk olacaktir Paylari ya da paydalari esit olmayan rasyonel sayilar 34 gt 210 displaystyle frac 3 4 gt frac 2 10 Bu sekildeki durumlarda karsilastirmadan evvel paydalarin esitlenmesi veya icler dislar carpimi yapilmasini gerektirir Paydalarin esitlenmesiHer iki rasyonel sayinin da birbirlerinin paydalariyla genisletilmesini gerektirir dd dd 34 gt 210 ise 3 104 10 gt 2 410 4 displaystyle frac 3 4 gt frac 2 10 mbox ise frac 3 cdot 10 4 cdot 10 gt frac 2 cdot 4 10 cdot 4 dd dd Yukarida goruldugu gibi genisletme isleminden sonra olusan paydalarin ikisi de 10 4 displaystyle 10 cdot 4 yani 40 tir Yukarida goruldugu gibi karsilastirilabilir dd dd Icler dislar carpimiBirinci rasyonel sayinin payinin ikincinin paydasina ikincinin paydasinin ise birincinin payiyla carpilmasidir dd dd 34 210 ise 3 10 4 2 buna gore 30 gt 8 displaystyle frac 3 4 cdot frac 2 10 mbox ise 3 cdot 10 4 cdot 2 mbox buna gore 30 gt 8 dd dd Toplama Iki kesrin toplanmasi su sekilde gerceklestirilir ab cd ad bcbd displaystyle frac a b frac c d frac ad bc bd Eger her iki kesir de kanonik formdaysa sonuc ancak ve ancak b d aralarinda asal tam sayilar olmasi durumunda kanonik formda olacaktir Cikarma ab cd ad bcbd displaystyle frac a b frac c d frac ad bc bd Eger her iki kesir de kanonik formdaysa sonuc ancak ve ancak b d aralarinda asal tam sayilar ise kanonik formdadir Carpma Carpma kurali su sekildedir ab cd acbd displaystyle frac a b cdot frac c d frac ac bd burada sonuc her iki orijinal kesir de kanonik formda olsa bile bir olabilir Tersi Herhangi bir rasyonel sayi ab displaystyle tfrac a b siklikla tersi olarak ifade edilen bir toplamin tersine sahiptir ab ab a bve ab 1 baegera 0 b 0 displaystyle left frac a b right frac a b frac a b quad mbox ve quad left frac a b right 1 frac b a quad mbox eger quad a neq 0 b neq 0 ab displaystyle tfrac a b kanonik formda ise onun karsitinin da kanonik formda olmasi ayni sekilde gecerlidir Sifirdan farkli bir rasyonel sayi ab displaystyle tfrac a b tersi olarak da adlandirilan bir sahiptir ab 1 ba displaystyle left frac a b right 1 frac b a ab displaystyle tfrac a b kanonik formda bulunuyorsa onun tersinin kanonik formu a degerinin isaretine gore ya ba displaystyle tfrac b a ya da b a displaystyle tfrac b a seklinde olur Bolme Eger b c d sifirdan farkliysa bolme kurali su sekildedir abcd adbc displaystyle frac dfrac a b dfrac c d frac ad bc ab cd adbc displaystyle frac a b div frac c d frac ad bc Boylece ab displaystyle tfrac a b yi cd displaystyle tfrac c d ile bolmek ab displaystyle tfrac a b yi cd displaystyle tfrac c d nin ile carpmakla esdegerdir adbc ab dc displaystyle frac ad bc frac a b cdot frac d c Tam sayi kuvvetine us alma n negatif olmayan bir tam sayi oldugunda ab n anbn displaystyle left frac a b right n frac a n b n Sonuc ab displaystyle tfrac a b icin ayni sekilde kanonik formda bulunuyorsa kanonik formdadir Belirli bir durum olarak ab 0 1 displaystyle left frac a b right 0 1 Eger a 0 o zaman ab n bnan displaystyle left frac a b right n frac b n a n Eger ab displaystyle tfrac a b kanonik formdaysa sonucun kanonik formu a gt 0 veya n cift ise bnan displaystyle tfrac b n a n olacaktir Aksi takdirde sonucun kanonik formu bn an displaystyle tfrac b n a n olur Surekli kesir gosterimiBir sonlu surekli kesir ifadesi asagidaki formda gosterilebilir a0 1a1 1a2 1 1an displaystyle a 0 cfrac 1 a 1 cfrac 1 a 2 cfrac 1 ddots cfrac 1 a n bu ifadede an tam sayilari temsil eder Herhangi bir rasyonel sayi ab displaystyle tfrac a b katsayilari an a b cifti uzerine Oklid algoritmasi uygulanarak elde edilebilen bir sonlu surekli kesir olarak gosterilebilir Diger gosterimlerBayagi kesir 83 displaystyle tfrac 8 3 Karmasik sayi 223 displaystyle 2 tfrac 2 3 Bir kullanilarak devirli sayi ile 2 6 displaystyle 2 overline 6 Parantez kullanilarak devirli sayi ile 2 6 displaystyle 2 6 Geleneksel tipografi kullanilarak 2 11 12 displaystyle 2 tfrac 1 1 tfrac 1 2 kisaltilmis notasyon ile surekli kesir 2 1 2 displaystyle 2 1 2 2 12 16 displaystyle 2 tfrac 1 2 tfrac 1 6 Asal us ayrisimi 23 3 1 displaystyle 2 3 times 3 1 3 6 displaystyle 3 6 ayni rasyonel degeri temsil etmenin farkli yollaridir TanimTam sayi ciftlerinin denklik siniflarinin gosterimini sunan bir diyagram Rasyonel sayilar tam sayilarin sirali ciftlerine dayanan denklik siniflari biciminde kurulabilir Daha kesin bir ifadeyle Z Z 0 displaystyle mathbb Z times mathbb Z setminus 0 kumesi n 0 olacak sekilde tam sayilarin m n ciftlerinin kumesi olarak alinsin Bu kume uzerinde bir denklik bagintisi m1 n1 m2 n2 m1n2 m2n1 displaystyle m 1 n 1 sim m 2 n 2 iff m 1 n 2 m 2 n 1 ile tanimlanmistir Toplama ve carpma islemleri asagidaki kurallarla tanimlanabilir m1 n1 m2 n2 m1n2 n1m2 n1n2 displaystyle m 1 n 1 m 2 n 2 equiv m 1 n 2 n 1 m 2 n 1 n 2 m1 n1 m2 n2 m1m2 n1n2 displaystyle m 1 n 1 times m 2 n 2 equiv m 1 m 2 n 1 n 2 Bu denklik iliskisi daha once tanimlanmis toplama ve carpma islemleriyle uyumlu bir olarak islev gorur boylece rasyonel sayilar kumesi Q displaystyle mathbb Q bu denklik iliskisine gore tanimlanan Z Z 0 displaystyle mathbb Z times mathbb Z backslash 0 sim formunda soz konusu islemler araciligiyla turetilmis toplama ve carpma islemleriyle zenginlestirilmistir Bu yapi herhangi bir tam bolge kullanilarak olusturulabilir ve soz konusu bolgenin meydana getirir Bir m n ciftinin denklik sinifi mn displaystyle tfrac m n seklinde ifade edilir m1 n1 ve m2 n2 ciftleri ancak ve ancak eger m1n2 m2n1 displaystyle m 1 n 2 m 2 n 1 ise ayni denklik sinifina dahildir yani esdegerdirler Bu durum m1n1 m2n2 displaystyle frac m 1 n 1 frac m 2 n 2 ancak ve ancak m1n2 m2n1 displaystyle m 1 n 2 m 2 n 1 oldugunda mumkundur Her denklik sinifi mn displaystyle tfrac m n sonsuz sayida cift tarafindan temsil edilebilir cunku 2m 2n m n mn 2m2n displaystyle cdots frac 2m 2n frac m n frac m n frac 2m 2n cdots Her denklik sinifi benzersiz bir kanonik temsilci elemani icerir Kanonik temsilci denklik sinifindaki m n benzersiz ciftidir oyle ki m ve n aralarinda asaldir ve n gt 0 Bu rasyonel sayinin olarak adlandirilir Tam sayilar tam sayi n yi rasyonel sayi n1 displaystyle tfrac n 1 ile ozdeslestirerek rasyonel sayilar olarak dusunulebilir Rasyonel sayilar uzerinde tam sayilarin dogal siralamasini genisleten bir tanimlanabilir Buna gore m1n1 m2n2 displaystyle frac m 1 n 1 leq frac m 2 n 2 Eger n1n2 gt 0vem1n2 n1m2 veya n1n2 lt 0vem1n2 n1m2 displaystyle begin aligned amp n 1 n 2 gt 0 quad text ve quad m 1 n 2 leq n 1 m 2 amp qquad text veya amp n 1 n 2 lt 0 quad text ve quad m 1 n 2 geq n 1 m 2 end aligned OzelliklerYukarida gosterilen toplama ve carpma islemleriyle birlikte tum rasyonel sayilarin kumesi Q displaystyle mathbb Q bir alan olusturur Q displaystyle mathbb Q ozdeslik disinda hicbir alan otomorfizmine sahip degildir Bir alan otomorfizmi 0 ve 1 i sabit tutmalidir iki sabit elemanin toplamini ve farkini sabit tutmak zorunda oldugundan her tam sayiyi sabit tutmalidir iki sabit elemanin bolumunu sabit tutmak zorunda oldugundan her rasyonel sayiyi sabit tutmali ve dolayisiyla ozdes olmalidir Q displaystyle mathbb Q kendisi disinda alt alani olmayan bir Rasyoneller sifir sahip en kucuk alandir Sifir karakteristige sahip her alan Q displaystyle mathbb Q ile izomorfik benzersiz bir alt alana sahiptir Yukarida tanimlanan sirayla Q displaystyle mathbb Q kendisi disinda alt alani olmayan bir ve her sirali alanin Q displaystyle mathbb Q ile benzersiz bir alt alani icerdigi anlaminda en kucuk sirali alandir Q displaystyle mathbb Q tam sayilarin Z displaystyle mathbb Z Q displaystyle mathbb Q nun yani rasyonel polinomlarin koklerinin alani cebirsel sayilar alanidir Rasyonel sayilar bir kumedir herhangi iki rasyonel sayi arasinda baska bir rasyonel sayi bulunur ve dolayisiyla sonsuz sayida baska rasyonel sayi bulunur Ornegin ab lt cd displaystyle frac a b lt frac c d b d displaystyle b d pozitif olmak uzere seklindeki herhangi iki kesir icin ab lt a cb d lt cd displaystyle frac a b lt frac a c b d lt frac c d En kucuk veya en buyuk elemani olmayan sayilabilir yogun yukaridaki anlamda ve tamamen sirali bir kume rasyonel sayilarla Sayilabilirlik Pozitif rasyonel sayilarin sayilabilirligini gosteren bir gosterims Tum rasyonel sayilar kumesinin sayilabilir oldugu sag tarafta yer alan gosterim ile aciklanmistir Her bir rasyonel sayinin iki tam sayinin orani seklinde ifade edilebilme ozelligi goz onunde bulunduruldugunda uzerindeki her bir noktaya bir Kartezyen koordinat sistemi benzeri bir yaklasimla iki tam sayi atanmasi mumkundur boylelikle her bir kafes noktasi bir rasyonel sayi ile iliskilendirilebilir Bu yontem saglanan grafikte kirmizi ile isaretlenmis olan bircok farkli kafes noktasinin ayni rasyonel sayiyi temsil etmesi gibi bir fazlaligin ortaya cikmasina neden olmaktadir Bu fazlaligin bir ornegi sag alt koseye dogru diagonal bir hat uzerinde gozlemlenebilir bu tur oranlar herhangi bir sayinin kendisi ile bolunmesi durumunda daima bir degerini alacaktir Bu tur fazlaliklar olmadan tum rasyonel sayilarin tanimi mumkundur ornekler arasinda ve bulunmaktadir Tum rasyonel sayilar kumesi sayilabilir oldugu ve tum reel sayilar kumesi ayni zamanda tum irrasyonel sayilar kumesi sayilamaz oldugu icin rasyonel sayilar kumesi bir yani anlaminda neredeyse tum reel sayilar irrasyoneldir Reel sayilar ve topolojik ozelliklerRasyonel sayilar reel sayilarin yogun bir alt kumesidir her reel sayinin yaninda keyfi olarak yakin rasyonel sayilar vardir Ilgili bir ozellik rasyonel sayilarin olarak genislemelere sahip tek sayilar olmasidir Reel sayilarin alisilageldik topolojisi icinde rasyonel sayilar ne bir acik kume ne de bir Siralarinin bir sonucu olarak rasyonel sayilar bir tasir Rasyonel sayilar reel sayilarin bir alt uzayi olarak ayrica bir altuzay topolojisi tasir Rasyonel sayilar metrigi d x y x y displaystyle d x y x y kullanilarak bir metrik uzay olusturur ve bu Q displaystyle mathbb Q uzerinde ucuncu bir topoloji saglar Bu uc topoloji cakisir ve rasyonelleri bir topolojik alana donusturur Rasyonel sayilar olmayan bir uzayin onemli bir ornegidir Rasyoneller topolojik olarak izole noktasi olmayan benzersiz olarak nitelendirilir Uzay ayrica Rasyonel sayilar tam metrik uzay olusturmaz ve reel sayilar yukarida verilen metrik d x y x y displaystyle d x y x y altinda Q displaystyle mathbb Q nun tamamlanmasidir p sel sayilarYukarida bahsedilen mutlak deger metrigine ek olarak Q displaystyle mathbb Q yu bir topolojik alan haline getiren diger metrikler de vardir p bir asal sayi olsun ve sifirdan farkli herhangi bir tam sayi a icin a p p n displaystyle a p p n burada pn a yi bolen p nin en yuksek kuvvetidir Ayrica 0 p 0 displaystyle 0 p 0 olarak belirleyelim Herhangi bir rasyonel sayi ab displaystyle frac a b icin ab p a p b p displaystyle left frac a b right p frac a p b p olarak belirleyelim O zaman dp x y x y p displaystyle d p x y x y p Q displaystyle mathbb Q uzerinde bir metrik tanimlar Metrik uzay Q dp displaystyle mathbb Q d p tam degildir ve tamamlanmis hali p adik sayi alani Qp displaystyle mathbb Q p dir rasyonel sayilar Q displaystyle mathbb Q uzerindeki herhangi bir onemli mutlak degerin ya alisilagelmis reel mutlak degere ya da bir p adik mutlak degere esdeger oldugunu belirtir Ayrica bakinizIrrasyonel sayilarSayi sistemleri Karmasik C displaystyle mathbb C Reel R displaystyle mathbb R Rasyonel Q displaystyle mathbb Q Tam sayi Z displaystyle mathbb Z Dogal N displaystyle mathbb N Sifir 0Bir 1Asal sayilarBilesik sayilarNegatif tam sayilarKesir Devirli ondalik sayiIrrasyonel Cebirsel irrasyonelAskinSanalNot listesi Bu kavram ilk kez Bourbaki tarafindan kaleme alinan Algebre isimli calismada ele alinmistir Kaynakca Rosen Kenneth 2007 Discrete Mathematics and its Applications 6 bas New York NY McGraw Hill ss 105 158 160 ISBN 978 0 07 288008 3 Rational number Encyclopedia Britannica Ingilizce 11 Aralik 2021 tarihinde kaynagindan Erisim tarihi 11 Agustos 2020 Weisstein Eric W Rational Number Wolfram MathWorld Ingilizce 14 Temmuz 2023 tarihinde kaynagindan Erisim tarihi 11 Agustos 2020 Rosen Kenneth 2007 Discrete Mathematics and its Applications 6 bas New York NY McGraw Hill ss 105 158 160 ISBN 978 0 07 288008 3 a b c d e f g h i j k l Biggs Norman L 2002 Discrete Mathematics India Oxford University Press ss 75 78 ISBN 978 0 19 871369 2 Robinson Julia 1996 The Collected Works of Julia Robinson Ingilizce American Mathematical Soc ISBN 978 0 8218 0575 6 Lass Harry 18 Kasim 2009 Elements of Pure and Applied Mathematics Ingilizce Courier Corporation ISBN 978 0 486 47186 0 Gilbert Jimmie 2005 Elements of Modern Algebra 6 6yayinci Thomson Brooks Cole bas Belmont CA ss 243 244 ISBN 0 534 40264 X a b Oxford English Dictionary 2 2tarih 1989 bas Oxford University Press 9 Mayis 2017 Does rational come from ratio or ratio come from rational Stack Exchange Ingilizce 17 Nisan 2021 tarihinde kaynagindan Erisim tarihi 19 Mart 2021 Coolman Robert 29 Ocak 2016 How a Mathematical Superstition Stultified Algebra for Over a Thousand Years Ingilizce 21 Aralik 2021 tarihinde kaynagindan Erisim tarihi 20 Mart 2021 Kramer Edna 1983 The Nature and Growth of Modern Mathematics Princeton University Press s 28 a b c d e f g h Fraction Encyclopedia of Mathematics encyclopediaofmath org 27 Eylul 2021 tarihinde kaynagindan Erisim tarihi 17 Agustos 2021 Sugakkai Nihon 1993 Encyclopedic Dictionary of Mathematics Volume 1 London England MIT Press s 578 ISBN 0 2625 9020 4 Giese Martin Schonegge Arno December 1995 Any two countable densely ordered sets without endpoints are isomorphic a formal proof with KIV PDF 25 Kasim 2021 tarihinde kaynagindan PDF Erisim tarihi 17 Agustos 2021 Anthony Vazzana David Garth 2015 Introduction to Number Theory 2nd revised bas CRC Press s 1 ISBN 978 1 4987 1752 6 Extract of page 1 Weisstein Eric W p adic Number Wolfram MathWorld Ingilizce 2 Mayis 2021 tarihinde kaynagindan Erisim tarihi 17 Agustos 2021 Dis baglantilarWikimedia Commons ta Rasyonel sayilar ile ilgili ortam dosyalari bulunmaktadir Vikiversite deRasyonel sayilar ile ilgili kaynaklar bulunur Hazewinkel Michiel Ed 2001 Rational number Encyclopaedia of Mathematics Kluwer Academic Publishers ISBN 978 1556080104 Rational Number From MathWorld A Wolfram Web Resource
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans