Radyal hız

Dikey hız (dikine hız veya görüş çizgisi hızı), bir hedefin bir gözlemciye göre iki nokta arasındaki vektörel yer değiştirme miktarının değişim hızıdır. Hedef-gözlemci , iki noktayı birleştiren izafi yön veya görüş çizgisi üzerindeki vektörel izdüşümü olarak tanımlanır. Daha basitçe, bir hedefin bir gözlemciye göre, görüş çizgisi boyunca yaklaşma veya uzaklaşma hızıdır.

Bir radar istasyonunun yanından geçen bir uçak. Uçağın hız vektörü (kırmızı), dikey hız (yeşil) ve teğetsel hızın (mavi) toplamıdır.

Astronomide nokta genellikle Dünya'daki gözlemci olarak alınır ve bu nedenle dikey hız, nesnenin Dünya'dan uzaklaşma (veya yaklaşma, negatif dikey hız için) hızını belirtir.

Bakış doğrultumuza göre eğimi dik olan bir yörünge etrafında dolanan bir cismi biz doğrudan baktığımızda ileri geri hareket eder gibi görürüz. Bu durumda cisim dikey olarak hareket eder gibi algılanır ve bu hareketin dönemi ile bağıntılı olarak dikine hız hesaplamaları yapılır.

İngilizcede kullanılan "radial velocity" ve "radial speed" terimleri farklı kavramlardır. "Radial velocity" için dikey hız kastedilirken, "radial speed" (veya "range rate") için bu konu bağlamında aralık hızı veya aralık oranı kullanılmaktadır.

Aralık hızı veya aralık oranı, iki nokta arasındaki mesafe veya aralığın zamana göre değişim hızı veya oranıdır. Bu, göreli hız vektörünün, gözlemci ile nesne arasındaki görüş çizgisi yönünde skaler izdüşümü olarak tanımlanan işaretli bir skaler büyüklüktür. Başka bir deyişle aralık hızı, dikey hızın büyüklüğüne eşittir; ancak, göreli hız ve göreli konumun geniş açı yapması durumunda, aralık hızının işareti değişir.

Formülasyon

Gözlemciye göre, bir hedefin anlık konumunu tanımlayan türevlenebilir bir vektör ${\displaystyle {\vec {r}}\in \mathbb {R} ^{3}}$ verilsin.

Formülleştirme

   

${\displaystyle {\vec {v}}={\frac {d{\vec {r}}}{dt}}}$

(1)

   

${\displaystyle {\vec {v}}\in \mathbb {R} ^{3}}$, hedefin gözlemciye göre anlık hızıdır.

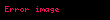
Pozisyon vektörü ${\displaystyle {\vec {r}}}$'nin büyüklüğü şöyle tanımlanır:

   

${\displaystyle r=|{\vec {r}}|=\langle {\vec {r}},{\vec {r}}\rangle ^{1/2}}$

(2)

   

Aralık oranı (Range rate), ${\displaystyle {\vec {r}}}$'nin büyüklüğünün () zaman türevi olarak ifade edilir

   

${\displaystyle {\frac {d{\vec {r}}}{dt}}}$

(3)

   

(2)'yi (3)'e yerine koyup

${\displaystyle {\frac {dr}{dt}}={\frac {d\langle {\vec {r}},{\vec {r}}\rangle ^{1/2}}{dt}}}$

Sağ tarafın türevini alırsak

${\displaystyle {\frac {dr}{dt}}={\frac {1}{2}}{\frac {d\langle {\vec {r}},{\vec {r}}\rangle }{dt}}{\frac {1}{r}}}$

${\displaystyle {\frac {dr}{dt}}={\frac {1}{2}}{\frac {\langle {\frac {d{\vec {r}}}{dt}},{\vec {r}}\rangle +\langle {\vec {r}},{\frac {d{\vec {r}}}{dt}}\rangle }{r}}}$

(1) denklemini kullanarak ifade şöyle olur

${\displaystyle {\frac {dr}{dt}}={\frac {1}{2}}{\frac {\langle {\vec {v}},{\vec {r}}\rangle +\langle {\vec {r}},{\vec {v}}\rangle }{r}}}$

Çünkü

${\displaystyle \langle {\vec {v}},{\vec {r}}\rangle =\langle {\vec {r}},{\vec {v}}\rangle }$

Ve

${\displaystyle {\hat {r}}={\frac {\vec {r}}{r}}}$

Aralık oranı basitçe şöyle tanımlanır

${\displaystyle {\frac {dr}{dt}}={\frac {\langle {\vec {r}},{\vec {v}}\rangle }{r}}=\langle {\hat {r}},{\vec {v}}\rangle }$

gözlemci ile hedef arasındaki hız vektörünün ${\displaystyle {\hat {r}}}$ birim vektörüne olan skaler izdüşümü

Gözlemci ile hedefin aynı noktada olduğu durumda, yani ${\displaystyle {\vec {r}}={\begin{bmatrix}0\ 0\ 0\end{bmatrix}}}$ olduğunda bir tekillik vardır. Bu durumda aralık oranı mevcut değildir, çünkü ${\displaystyle r=0}$'dır.

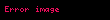
Astronomideki Uygulamaları

Astronomide dikine hız genellikle Doppler spektroskopisinin birinci yaklaşımına göre ölçülür. Bu yöntemle elde edilen dikine hız miktarına barisentrik dikine hız veya spektroskopik dikine hız denir. Ancak ışığın uzak bir mesafeden gelirken kat ettiği yolda geçen zaman ve kozmolojik etkiler göz önüne alındığında bu ölçüm gözlemci ve ışık kaynağı arasındaki boşluğun uzunluğu ve yapısı hakkında kesin bir bilgi olmadığı müddetçe nesnenin geometrik dikine hızına dönüştürülemez. Buna karşılık gökbilimsel dikine hız gözlemlerle belirlenebilir (örneğin: yıllık paralaksta gerçekleşen uzun süreli bir değişim).

Spektroskopik Dikey Hız

Işık, yüksek bir dikine hıza sahip kaynaktan çıkarken Doppler etkisine maruz kalacaktır. Dolayısıyla ışığın dalga boyu uzaklaşan nesneler için artarken (kırmızıya kayma) yakınlaşan nesneler için azalacaktır (maviye kayma). Bir nesnenin su üzerinde gözlemciye yaklaşırken gözlemciye doğru gelen dalgaların kısalıp, gözlemciden uzaklaşırken oluşturduğu dalgaların uzaması buna örnek olarak verilebilir. Bir yıldızın dikine hızı yüksek çözünürlüklü bir spektrum alınarak (tayfçeker ile) ölçülebilir. Bilinen tayf çizgilerinden yola çıkarak yıldızdan alınan tayfta oluşan kaymalar karşılaştırıldığında yıldızın dikine hızı ölçülebilir. Pozitif bir dikey hız, nesneler arasındaki mesafenin arttığını veya artmakta olduğunu, negatif bir dikey hız ise kaynak ile gözlemci arasındaki mesafenin azaldığını veya azalmakta olduğunu gösterir.

William Huggins, 1886'da yıldız ışığında gözlemlenen kırmızıya kaymayı temel alarak Sirius yıldızının Güneş'e göre dikine hızını tahmin etme girişiminde bulundu.

Ayrıca bakınız

• Özdevinim
• Doppler etkisi
• Lp uzayı

Notlar

1. ^ iki nokta arasındaki mesafenin zamana bağlı değişim oranı

Kaynakça

1. ^ (PDF). 20 Kasım 2016 tarihinde kaynağından (PDF) arşivlendi. 
2. ^ Hoffman, Kenneth M.; Kunzel, Ray (1971). Linear Algebra (İkinci bas.). Prentice-Hall Inc. s. 1 271. ISBN . 
3. ^ Ferrero, Miguel (1 Ocak 2003). "Special Issue: International Conference on Quantum Information. Conceptual Foundations, Developments and Perspectives, 13-18 July 2002". Journal of Modern Optics. 50 (6-7): 867-871. doi:10.1080/0950034031000064807. ISSN 0950-0340. 
4. ^ Lindegren, Lennart; Dravins, Dainis (Nisan 2003). "The fundamental definition of "radial velocity"". Astronomy & Astrophysics. 401 (3): 1185-1201. doi:10.1051/0004-6361:20030181. ISSN 0004-6361. 
5. ^ Dravins, Dainis; Gullberg, Dag; Lindegren, Lennart; Madsen, Søren (1999). "Astrometric versus Spectroscopic Radial Velocities". International Astronomical Union Colloquium. 170: 41-47. doi:10.1017/s0252921100048326. ISSN 0252-9211. 20 Mart 2022 tarihinde kaynağından . Erişim tarihi: 13 Şubat 2024. 
6. ^ "1.9. IAU Symposium no.99: Wolf-rayet stars: Observations, physics and evolution". COSPAR Information Bulletin. 1981 (91): 13. Ağustos 1981. doi:10.1016/0045-8732(81)90009-7. ISSN 0045-8732. 
7. ^ Huggins, William (31 Aralık 1868). "XXI. Further observations on the spectra of some the stars and nebulæ, with an attempt to determine therefrom whether these bodies are moving towards or from the earth, also observations on the spectra of the sun and of comet II., 1868". Philosophical Transactions of the Royal Society of London (İngilizce). 158: 529-564. doi:10.1098/rstl.1868.0022. ISSN 0261-0523. 10 Şubat 2022 tarihinde kaynağından . Erişim tarihi: 13 Şubat 2024.