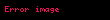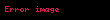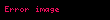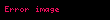Spiral matematikte, bir merkez noktadan doğan, bu nokta etrafında dönerek kademeli olarak uzaklaşan bir eğridir.


İki boyutlu spiraller
İki boyutlu spiraller, r yarıçapı θ açısının tekdüze bir sürekli fonksiyonu iken; kutupsal koordinat sistemi ile açıklanabilir.
Bir daire, bu fonksiyonun monoton (tekdüze) değil sabit olduğu özel bir durumudur.
İki boyutlu spirallerin önemli türlerinden bazıları şunlardır:
- Arşimet spirali:
(ayrıca bakınız:)
- Euler spirali, Cornu spirali ya da clothoid
- :
- The hiperbolik spiral:
- :
- logaritmik spiral:
; bunun yaklaşık değerleri doğada bulunur.
- ve : Logaritmik spiralin özel bir durumudur (ayrıca bakınız: altın oran)
- Theodorus’un Spirali: bitişik sağ üçgenlerden meydana gelen bir Arşimet spirali yakınsamasıdır.
- Bir dairenin , hemen hemen her modern dişlinin her dişinde iki defa kullanılır.
-
![image]() Arşimet spirali
Arşimet spirali -
![image]() Cornu ya da Euler spirali
Cornu ya da Euler spirali -
![image]() Fermat spirali
Fermat spirali -
![image]() Hiperbolik spiral
Hiperbolik spiral -
![image]() Lituus
Lituus -
![image]() Logaritmik spiral
Logaritmik spiral -
![image]() Theodorus’un Spirali
Theodorus’un Spirali -
![image]() Dairenin involütü (siyah) Arşimet spirali (kırmızı) ile özdeş değildir.
Dairenin involütü (siyah) Arşimet spirali (kırmızı) ile özdeş değildir.
Üç boyutlu spiraller

Basit 3-d spiraller için, üçüncü değişken, h (yükseklik) de θ açısının tekdüze bir sürekli fonksiyonudur. Örneğin, bir konik sarmal bir konik yüzey üzerinde, apexe mesafesi θnın üstel bir fonksiyonu olan bir spiral olarak tanımlanabilir.
Sarmal ve girdap üç boyutlu spirallerin bir çeşidi olarak görülebilir.
Ayrıca bakınız
İlişkili yayınlar
- Cook, T., 1903. Spirals in nature and art. Nature 68 (1761), 296.
- Cook, T., 1979. The curves of life. Dover, New York.
- Habib, Z., Sakai, M., 2005. Spiral transition curves and their applications. Scientiae Mathematicae Japonicae 61 (2), 195 – 206.
- Dimulyo, S., Habib, Z., Sakai, M., 2009. Fair cubic transition between two circles with one circle inside or tangent to the other. Numerical Algorithms 51, 461–476 [1] 27 Kasım 2018 tarihinde Wayback Machine sitesinde ..
- Harary, G., Tal, A., 2011. The natural 3D spiral. Computer Graphics Forum 30 (2), 237 – 246 [2] 22 Kasım 2015 tarihinde Wayback Machine sitesinde ..
- Xu, L., Mould, D., 2009. Magnetic curves: curvature-controlled aesthetic curves using magnetic fields. In: Deussen, O., Hall, P. (Eds.), Computational Aesthetics in Graphics, Visualization, and Imaging. The Eurographics Association [3] 3 Mart 2016 tarihinde Wayback Machine sitesinde ..
- Wang, Y., Zhao, B., Zhang, L., Xu, J., Wang, K., Wang, S., 2004. Designing fair curves using monotone curvature pieces. Computer Aided Geometric Design 21 (5), 515–527 [4] 24 Eylül 2015 tarihinde Wayback Machine sitesinde ..
- A. Kurnosenko. Applying inversion to construct planar, rational spirals that satisfy two-point G2 Hermite data. Computer Aided Geometric Design, 27(3), 262–280, 2010 [5] 24 Eylül 2015 tarihinde Wayback Machine sitesinde ..
- A. Kurnosenko. Two-point G2 Hermite interpolation with spirals by inversion of hyperbola. Computer Aided Geometric Design, 27(6), 474–481, 2010.
- Miura, K.T., 2006. A general equation of aesthetic curves and its self-affinity. Computer-Aided Design and Applications 3 (1–4), 457–464 .
- Miura, K., Sone, J., Yamashita, A., Kaneko, T., 2005. Derivation of a general formula of aesthetic curves. In: 8th International Conference on Humans and Computers (HC2005). Aizu-Wakamutsu, Japan, pp. 166 – 171 .
- Meek, D., Walton, D., 1989. The use of Cornu spirals in drawing planar curves of controlled curvature. Journal of Computational and Applied Mathematics 25 (1), 69–78 [8] 24 Eylül 2015 tarihinde Wayback Machine sitesinde ..
- Farin, G., 2006. Class A Bézier curves. Computer Aided Geometric Design 23 (7), 573–581 [9] 24 Eylül 2015 tarihinde Wayback Machine sitesinde ..
- Farouki, R.T., 1997. Pythagorean-hodograph quintic transition curves of monotone curvature. Computer-Aided Design 29 (9), 601–606.
- Yoshida, N., Saito, T., 2006. Interactive aesthetic curve segments. The Visual Computer 22 (9), 896–905 [10] 4 Mart 2016 tarihinde Wayback Machine sitesinde ..
- Yoshida, N., Saito, T., 2007. Quasi-aesthetic curves in rational cubic Bézier forms. Computer-Aided Design and Applications 4 (9–10), 477–486 [11] 3 Mart 2016 tarihinde Wayback Machine sitesinde ..
- Ziatdinov, R., Yoshida, N., Kim, T., 2012. Analytic parametric equations of log-aesthetic curves in terms of incomplete gamma functions. Computer Aided Geometric Design 29 (2), 129 – 140 [12] 24 Eylül 2015 tarihinde Wayback Machine sitesinde ..
- Ziatdinov, R., Yoshida, N., Kim, T., 2012. Fitting G2 multispiral transition curve joining two straight lines, Computer-Aided Design 44(6), 591–596 [13] 24 Eylül 2015 tarihinde Wayback Machine sitesinde ..
- Ziatdinov, R., 2012. Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function. Computer Aided Geometric Design 29(7): 510–518 [14] 24 Eylül 2015 tarihinde Wayback Machine sitesinde ..
- Ziatdinov, R., Miura K.T., 2012. On the Variety of Planar Spirals and Their Applications in Computer Aided Design. European Researcher 27(8–2), 1227-–1232 [15]23 Temmuz 2020 tarihinde Wayback Machine sitesinde ..
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Spiral matematikte bir merkez noktadan dogan bu nokta etrafinda donerek kademeli olarak uzaklasan bir egridir Bir notilus kabugunun kesitinde logaritmik spiral seklinde dizilmis bolmelerBir Arsimet spirali bir sarmal ve konik spiralIki boyutlu spirallerIki boyutlu spiraller r yaricapi 8 acisinin tekduze bir surekli fonksiyonu iken kutupsal koordinat sistemi ile aciklanabilir Bir daire bu fonksiyonun monoton tekduze degil sabit oldugu ozel bir durumudur Iki boyutlu spirallerin onemli turlerinden bazilari sunlardir Arsimet spirali r a b 8 displaystyle r a b cdot theta ayrica bakiniz Euler spirali Cornu spirali ya da clothoid r 81 2 displaystyle r theta 1 2 The hiperbolik spiral r a 8 displaystyle r a theta r 8 1 2 displaystyle r theta 1 2 logaritmik spiral r a eb8 displaystyle r a cdot e b theta bunun yaklasik degerleri dogada bulunur ve Logaritmik spiralin ozel bir durumudur ayrica bakiniz altin oran Theodorus un Spirali bitisik sag ucgenlerden meydana gelen bir Arsimet spirali yakinsamasidir Bir dairenin hemen hemen her modern dislinin her disinde iki defa kullanilir Arsimet spirali Cornu ya da Euler spirali Fermat spirali Hiperbolik spiral Lituus Logaritmik spiral Theodorus un Spirali Dairenin involutu siyah Arsimet spirali kirmizi ile ozdes degildir Uc boyutlu spirallerKerte hattiArsimet spiraliBir kure yuzeyi uzerinde iki farkli cesit spiral Basit 3 d spiraller icin ucuncu degisken h yukseklik de 8 acisinin tekduze bir surekli fonksiyonudur Ornegin bir konik sarmal bir konik yuzey uzerinde apexe mesafesi 8nin ustel bir fonksiyonu olan bir spiral olarak tanimlanabilir Sarmal ve girdap uc boyutlu spirallerin bir cesidi olarak gorulebilir Ayrica bakinizFibonacci dizisiIliskili yayinlarCook T 1903 Spirals in nature and art Nature 68 1761 296 Cook T 1979 The curves of life Dover New York Habib Z Sakai M 2005 Spiral transition curves and their applications Scientiae Mathematicae Japonicae 61 2 195 206 Dimulyo S Habib Z Sakai M 2009 Fair cubic transition between two circles with one circle inside or tangent to the other Numerical Algorithms 51 461 476 1 27 Kasim 2018 tarihinde Wayback Machine sitesinde Harary G Tal A 2011 The natural 3D spiral Computer Graphics Forum 30 2 237 246 2 22 Kasim 2015 tarihinde Wayback Machine sitesinde Xu L Mould D 2009 Magnetic curves curvature controlled aesthetic curves using magnetic fields In Deussen O Hall P Eds Computational Aesthetics in Graphics Visualization and Imaging The Eurographics Association 3 3 Mart 2016 tarihinde Wayback Machine sitesinde Wang Y Zhao B Zhang L Xu J Wang K Wang S 2004 Designing fair curves using monotone curvature pieces Computer Aided Geometric Design 21 5 515 527 4 24 Eylul 2015 tarihinde Wayback Machine sitesinde A Kurnosenko Applying inversion to construct planar rational spirals that satisfy two point G2 Hermite data Computer Aided Geometric Design 27 3 262 280 2010 5 24 Eylul 2015 tarihinde Wayback Machine sitesinde A Kurnosenko Two point G2 Hermite interpolation with spirals by inversion of hyperbola Computer Aided Geometric Design 27 6 474 481 2010 Miura K T 2006 A general equation of aesthetic curves and its self affinity Computer Aided Design and Applications 3 1 4 457 464 Miura K Sone J Yamashita A Kaneko T 2005 Derivation of a general formula of aesthetic curves In 8th International Conference on Humans and Computers HC2005 Aizu Wakamutsu Japan pp 166 171 Meek D Walton D 1989 The use of Cornu spirals in drawing planar curves of controlled curvature Journal of Computational and Applied Mathematics 25 1 69 78 8 24 Eylul 2015 tarihinde Wayback Machine sitesinde Farin G 2006 Class A Bezier curves Computer Aided Geometric Design 23 7 573 581 9 24 Eylul 2015 tarihinde Wayback Machine sitesinde Farouki R T 1997 Pythagorean hodograph quintic transition curves of monotone curvature Computer Aided Design 29 9 601 606 Yoshida N Saito T 2006 Interactive aesthetic curve segments The Visual Computer 22 9 896 905 10 4 Mart 2016 tarihinde Wayback Machine sitesinde Yoshida N Saito T 2007 Quasi aesthetic curves in rational cubic Bezier forms Computer Aided Design and Applications 4 9 10 477 486 11 3 Mart 2016 tarihinde Wayback Machine sitesinde Ziatdinov R Yoshida N Kim T 2012 Analytic parametric equations of log aesthetic curves in terms of incomplete gamma functions Computer Aided Geometric Design 29 2 129 140 12 24 Eylul 2015 tarihinde Wayback Machine sitesinde Ziatdinov R Yoshida N Kim T 2012 Fitting G2 multispiral transition curve joining two straight lines Computer Aided Design 44 6 591 596 13 24 Eylul 2015 tarihinde Wayback Machine sitesinde Ziatdinov R 2012 Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function Computer Aided Geometric Design 29 7 510 518 14 24 Eylul 2015 tarihinde Wayback Machine sitesinde Ziatdinov R Miura K T 2012 On the Variety of Planar Spirals and Their Applications in Computer Aided Design European Researcher 27 8 2 1227 1232 15 23 Temmuz 2020 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans