Logaritmik spiral

Logaritmik (veya eşaçılı) spiral, doğada sık rastlanan bir spiral çeşididir. İlk olarak 17. yüzyılda René Descartes ve Jakob Bernoulli tarafından tanımlanmış ve incelenmiştir. Bernoulli bu eğriye, kendine özgü matematiksel özelliklerinden dolayı, spira mirabilis (mucizevi spiral) adını vermiş ve mezar taşına bir logaritmik spiral oyulmasını vasiyet etmiştir.

Bir logaritmik spiral

Bir notilus kabuğunun kesitinde, logaritmik spiral şeklinde dizilmiş bölmeler

İzlanda üzerinde, logaritmik spiral şekli almış bir alçak basınç alanı

Kolları logaritmik spiral şeklinde şekillenmiş olan Messier 51a gökadası

Denizatı kuyruğu

Kutupsal koordinat sisteminde logaritmik spiral şu eşitlikle ifade edilir:

${\displaystyle \,r=ae^{b\theta }.}$

Burada a ve b gerçel parametreler, e ise Euler sayısıdır. Aynı eşitlik şu şekilde de yazılabilir:

${\displaystyle \theta ={\frac {1}{b}}\ln(r/a),}$

nitekim logaritmik ismi de buradan gelir. Kartezyen koordinat sisteminde aynı eğri, şu parametrik denklem çiftiyle ifade edilebilir:

${\displaystyle x(t)=ae^{bt}\cos(t),\,}$

${\displaystyle y(t)=ae^{bt}\sin(t).\,}$

Özellikler

Altın bölüm

Logaritmik spiralin ilginç özelliklerinden biri, orijinden çıkan her doğrunun spirali aynı açıyla kesmesidir. Bir başka deyişle, orijinden çıkan her doğru, spirali kestiği her noktada, spirale teğet geçen doğruyu aynı açıyla keser. Logaritmik spirale eşaçılı denmesinin sebebi de budur. Bu kesme açısı, vektör hesabı yardımıyla bulunabilir:

${\displaystyle \phi =\arccos {\frac {\langle \mathbf {r} (\theta ),\mathbf {r} '(\theta )\rangle }{\|\mathbf {r} (\theta )\|\|\mathbf {r} '(\theta )\|}}=\arctan {\frac {1}{b}}\,.}$

Bu formüle göre, b^,yi sıfır aldığımızda orijinden çıkan doğrular spirali hep dik kesecektir, yani spiral a yarıçaplı bir çemberdir. (Elbette aynı sonuç polar denklemde b'yi sıfır alarak da görülebilir.)

Orijinden çıkan herhangi bir doğrunun logaritmik spirali kestiği noktalar, bir geometrik dizi halinde birbirlerinden uzaklaşırlar. Her bir noktanın orijine uzaklığı, bir önceki noktanın orijine uzaklığının 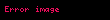${\displaystyle \,e^{2\pi b}}$ katıdır. Bir başka spiral çeşidi olan Arşimet spiralinde ise bu noktaların arasındaki mesafe hep aynı kalır.

Logaritmik spiral üzerinde sabit bir noktadan hareket edip spiral boyunca orijine doğru ilerlersek, orijine varmadan önce çevresini sonsuz kere turlamamız gerekir, fakat katedeceğimiz toplam mesafe sonludur: 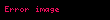${\displaystyle \,r/\cos(\phi )}$. (Burada r başlangıç noktasının orijine uzaklığıdır.) Bu şaşırtıcı sonucu ilk keşfeden, 17. yüzyıl matematikçisi Evangelista Torricelli olmuştur.

Logaritmik spiralin bulunduğu düzlemin ölçeğini değiştirmek, spirali orijin çevresinde döndürmekle aynı sonucu verir. n bir tam sayı olmak üzere, ölçeği 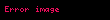${\displaystyle \,e^{2n\pi b}}$ oranında büyütmek ya da küçültmek, spirali orijin çevresinde n tam tur döndürmekle aynı şeydir ve bize orijinal spiralin aynısını verir. Dolayısıyla logaritmik spiral, basit bir fraktal örneğidir.

Doğada logaritmik spiral

Logaritmik spiral, doğada rastlanan pek çok süreçte kendiliğinden oluşur.

• Bir şahin, havadan avına yaklaşırken logaritmik spiral izler. Şahinin avını en iyi görebildiği açı sabittir ve şahin uçuş yönünü, bu açıyı sabit tutacak şekilde belirler. Bu da bir logaritmik spiral oluşturur.
• Uçabilen böcekler, bir ışık kaynağına yaklaşırken logaritmik spiral izlerler. Bunun sebebi, ışık kaynağı ve uçuş yönleri arasındaki açıyı sabit tutmalarıdır. (Doğada tek kuvvetli ışık kaynağı güneş ya da ay olduğundan, ışık kaynağına sabit bir açıyla uçmak böceklerin dümdüz ilerlemesini sağlar. Yapay ışık kaynaklarına sabit bir açıyla ilerlemek ise düz bir hat yerine logaritmik spiral oluşturur.)
• Sarmal gökadaların kolları logaritmik spiral şeklinde açılır. İçinde bulunduğumuz Samanyolu gökadası da dört ana kolu olan bir sarmal gökadadır.
• Tropik kasırgalar logaritmik spiral şeklini alırlar.
• Notilus gibi pek çok deniz canlısı, kabuğunu logaritmik spiral şeklinde inşa eder. Bunun sebebi, bu hayvanların büyüme hızlarının mevcut büyüklüklerine orantılı olması, yani hayvanların üstel bir hızla büyümeleridir.

Ayrıca bakınız

• Arşimet spirali
• Hiperbolik spiral

Kaynakça

• MathWorld'den logaritmik spiral 11 Mayıs 2000 tarihinde Wayback Machine sitesinde . sayfası (İngilizce)
• MacTutor Matematik Tarihi Arşivi'nden logaritmik spiral 10 Haziran 2007 tarihinde Wayback Machine sitesinde . sayfası (İngilizce)

Dış bağlantılar

• Logaritmik spiral ve özellikleri 15 Temmuz 2007 tarihinde Wayback Machine sitesinde . (İngilizce)
• Logaritmik spiralin ölçeğini değiştirmeye yarayan bir applet uygulaması 15 Temmuz 2007 tarihinde Wayback Machine sitesinde . (İngilizce)
• Kabuklu hayvanlarda logaritmik spirali inceleyen bir yazı 4 Ağustos 2007 tarihinde Wayback Machine sitesinde . (İngilizce)