Matematikte, görüntü kümesi sınırlı olan bir fonksiyonlara sınırlı fonksiyon denir. Sınırlılık özelliği, analiz başta olmak üzere matematiğin analizle irtibatı olan hemen hemen her alanında kullanılan temel bir özelliktir.

Tanım
Bir 



bütün 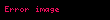

Alttan ve üstten sınırlılık
Eğer fonksiyon gerçel değerliyse ve 
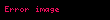



Sınırlı diziler







eşitsizliğini sağlayan bir 
Sınırlılığın genelleştirilmesi
Sınırlılık görüntü kümesinin gerçel ya da karmaşık sayılar olmadığı durumlara da genelleştirilebilir. Bu tür genelleştirmelerede, bir değer kümesi 



kümesi
normuna sahip bir normlu uzay ise,
- özelliği istenir.
metrik uzaysa; yani, üzerinde
metriği tanımlıysa, o zaman,
- özelliği istenir.
Her ne kadar, bu genellemeler 



Bir 






Örnekler
- Sinüs fonksiyonu
sınırlı bir fonksiyondur; çünkü, her
için
sağlanır.
fonksiyonu −1 ve 1 haricindeki tüm
değerleri için tanımlıdır; ancak, fonksiyon sınırlı bir fonksiyon değildir.
−1 ya da 1 değerine yaklaştığında, fonksiyonun değerleri kontrolsüzce büyür ve herhangi sabit bir sayıdan küçük olamaz. Yine de, bu tip fonksiyonları problemli uzak tutup daha dar tanım kümelerinde sınırlı yapmak mümkündür. Örneğin, fonksiyonu sadece
kümesi üzerinde kısıtlarsak, o zaman, fonksiyonun değerleri
ve
değerleri arasında olacaktır ve sonuç olarak fonksiyon sınırlı olacaktır.
fonksiyonu tüm
değerleri için tanımlıdır ve her
için
olduğundan fonksiyon sınırlıdır. Fonksiyonun her zaman 1'den küçük olduğu paydanın nerede en küçük değeri aldığı düşünülerek elde edilebilir.
veya
olarak tanımlı ters tanjant fonksiyonu bütün gerçel
değerleri için tanımlıdır. Bu fonksiyon, geçel sayılar üzerinde kesin artan bir fonksiyondur ve
özelliği sağlanır. Bu yüzden, ters tanjant fonksiyonu sınırlı bir fonksiyondur.
- sayesinde, iki tarafından kapalı bir aralık üzerinde tanımlı her sürekli fonksiyon sınırlıdır. Bu özelliğin tıkız uzaylara da genelleştirmesi vardır. Yâni, tıkız bir metrik uzaydan bir metrik uzaya tanımlı sürekli fonksiyonlar da yine sınırlıdır.
- Sabit olmayan tam fonksiyonlar Liouville teoremi sayesinde sınırlı olamazlar.
Ayrıca bakınız
Kaynakça
- ^ TÜBA Akademik Bilim Terimleri Sözlüğü'nde sınırlı fonksiyon sayfası
- ^ "The Sine and Cosine Functions" (PDF). math.dartmouth.edu. 2 Şubat 2013 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 1 Eylül 2021.
- ^ Polyanin, Andrei D.; Chernoutsan, Alexei (18 Ekim 2010). A Concise Handbook of Mathematics, Physics, and Engineering Sciences (İngilizce). CRC Press. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte goruntu kumesi sinirli olan bir fonksiyonlara sinirli fonksiyon denir Sinirlilik ozelligi analiz basta olmak uzere matematigin analizle irtibati olan hemen hemen her alaninda kullanilan temel bir ozelliktir Sinirli bir fonksiyonun kirmizi ve sinirsiz bir fonksiyonun mavi sematik gosterimi Sezgisel olarak sinirli bir fonksiyonun grafigi yatay bir bant icinde kalirken sinirsiz bir fonksiyonun grafigi kalmaz TanimBir f displaystyle f fonksiyonu bir X displaystyle X kumesi uzerinde tanimliysa ve X displaystyle X kumesi uzerinde gercel ya da karmasik deger alip da pozitif bir M displaystyle M degeri icin f x M displaystyle f x leq M butun x X displaystyle x in X icin saglaniyorsa o zaman f displaystyle f fonksiyonu sinirli bir fonksiyondur Bir fonksiyonun verilen bir kume uzerindeki degerleri siirli bir kumede yer almiyorsa fonksiyona sinirsiz fonksiyon ya da sinirli olmayan fonksiyon denilir Alttan ve ustten sinirlilik Eger fonksiyon gercel degerliyse ve f x M displaystyle f x leq M her x X displaystyle x in X icin saglaniyorsa o zaman fonksiyona ustten sinirli fonksiyon denir ve M displaystyle M bu fonksiyonun ust siniri olur Benzer bir sekilde eger fonksiyon gercel degerliyse ve f x m displaystyle f x geq m her x X displaystyle x in X icin saglaniyorsa o zaman fonksiyona alttan sinirli fonksiyon denir ve m displaystyle m bu fonksiyonun alt siniri olur Sinirli diziler X displaystyle X kumesi dogal sayilar kumesi N displaystyle mathbb N oldugunda fonksiyon ozel bir hal alir ve gercel ya da karmasik degerli bir dizi olur Bu durumda bu fonksiyonun goruntu kumesi ile gosterimi olur ve genelde a0 a1 a2 displaystyle a 0 a 1 a 2 ldots ya da ai i 1 displaystyle a i i 1 infty gibi gosterimler mevcuttur Sonuc olarak X displaystyle X kumesi dogal sayilar kumesi N displaystyle mathbb N oldugunda sinirli fonksiyona sinirli dizi denir ve her n N displaystyle n in mathbb N icin an M displaystyle a n leq M esitsizligini saglayan bir M displaystyle M sayisi vardir Sinirliligin genellestirilmesi Sinirlilik goruntu kumesinin gercel ya da karmasik sayilar olmadigi durumlara da genellestirilebilir Bu tur genellestirmelerede bir deger kumesi Y displaystyle Y nin daha genel oldugu durumlarda f X Y displaystyle f X rightarrow Y fonksiyonu icin f X displaystyle f X goruntu kumesinin Y displaystyle Y icinde sinirli olmasi istenir Ornegin Y displaystyle Y kumesi displaystyle cdot normuna sahip bir normlu uzay ise sup f x x X lt displaystyle sup f x x in X lt infty ozelligi istenir Y displaystyle Y metrik uzaysa yani uzerinde d displaystyle d metrigi tanimliysa o zaman diam f X sup d f x f y x y X lt displaystyle operatorname diam f X sup d f x f y x y in X lt infty ozelligi istenir Her ne kadar bu genellemeler X displaystyle X tannim kumesinden bagimsiz verilmis olsa da Y displaystyle Y nin yukaridaki gibi oldugu durumlarda X displaystyle X de daha ozel bir durumda olur ve f displaystyle f fonksiyonu genelde ozel adlar alir Ornegin bir Banach uzayindan karmasik sayilara alinan dogrusal fonksiyonlara ya da kisaca denir Bir X displaystyle X kumesinden bir S displaystyle S kumesine tanimli butun sinirli fonksiyonlarin kumesi genelde sinrli kelimesinin Ingilizce bounded kelimesine karsilik gelmesine binaen B X S displaystyle B X S ile gosterilir Eger S C displaystyle S mathbb C ya da S R displaystyle S mathbb R ise ya da S displaystyle S kumesinin ne oldugu icerikten acik bir sekilde anlasiliyorsa sadece B X displaystyle B X de yazilir OrneklerSinus fonksiyonu sin R R displaystyle sin mathbb R rightarrow mathbb R sinirli bir fonksiyondur cunku her x R displaystyle x in mathbb R icin sin x 1 displaystyle sin x leq 1 saglanir f x x2 1 1 displaystyle f x x 2 1 1 fonksiyonu 1 ve 1 haricindeki tum x displaystyle x degerleri icin tanimlidir ancak fonksiyon sinirli bir fonksiyon degildir x displaystyle x 1 ya da 1 degerine yaklastiginda fonksiyonun degerleri kontrolsuzce buyur ve herhangi sabit bir sayidan kucuk olamaz Yine de bu tip fonksiyonlari problemli uzak tutup daha dar tanim kumelerinde sinirli yapmak mumkundur Ornegin fonksiyonu sadece 2 displaystyle 2 infty kumesi uzerinde kisitlarsak o zaman fonksiyonun degerleri 13 displaystyle frac 1 3 ve 0 displaystyle 0 degerleri arasinda olacaktir ve sonuc olarak fonksiyon sinirli olacaktir f x x2 1 1 textstyle f x x 2 1 1 fonksiyonu tum x displaystyle x degerleri icin tanimlidir ve her x displaystyle x icin f x 1 textstyle f x leq 1 oldugundan fonksiyon sinirlidir Fonksiyonun her zaman 1 den kucuk oldugu paydanin nerede en kucuk degeri aldigi dusunulerek elde edilebilir y arctan x displaystyle y arctan x veya x tan y displaystyle x tan y olarak tanimli ters tanjant fonksiyonu butun gercel x displaystyle x degerleri icin tanimlidir Bu fonksiyon gecel sayilar uzerinde kesin artan bir fonksiyondur ve p2 lt y lt p2 displaystyle frac pi 2 lt y lt frac pi 2 ozelligi saglanir Bu yuzden ters tanjant fonksiyonu sinirli bir fonksiyondur sayesinde iki tarafindan kapali bir aralik uzerinde tanimli her surekli fonksiyon sinirlidir Bu ozelligin tikiz uzaylara da genellestirmesi vardir Yani tikiz bir metrik uzaydan bir metrik uzaya tanimli surekli fonksiyonlar da yine sinirlidir Sabit olmayan tam fonksiyonlar Liouville teoremi sayesinde sinirli olamazlar Ayrica bakinizSinirli kumeKaynakca TUBA Akademik Bilim Terimleri Sozlugu nde sinirli fonksiyon sayfasi The Sine and Cosine Functions PDF math dartmouth edu 2 Subat 2013 tarihinde kaynagindan arsivlendi PDF Erisim tarihi 1 Eylul 2021 Polyanin Andrei D Chernoutsan Alexei 18 Ekim 2010 A Concise Handbook of Mathematics Physics and Engineering Sciences Ingilizce CRC Press ISBN 978 1 4398 0640 1
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State